Логика и компьютер

1.

ЛОГИКА И КОМПЬЮТЕР

2.

3.

λόγος
(греч.)
«мысль, рассуждение»

4.

4
Логика и формальная логика
Логика – это наука о том,
как правильно рассуждать,
делать выводы,
доказывать утверждения.
Формальная логика отвлекается
от конкретного содержания,
изучает только истинность и
ложность высказываний.

5.

Аристотель
(384-322 гг. до н.э.)
основоположник
формальной логики

6.

6
Высказывание и логическое высказывание
Логическое высказывание – это повествовательное
предложение, относительно которого можно
однозначно сказать, истинно оно или ложно.

7.

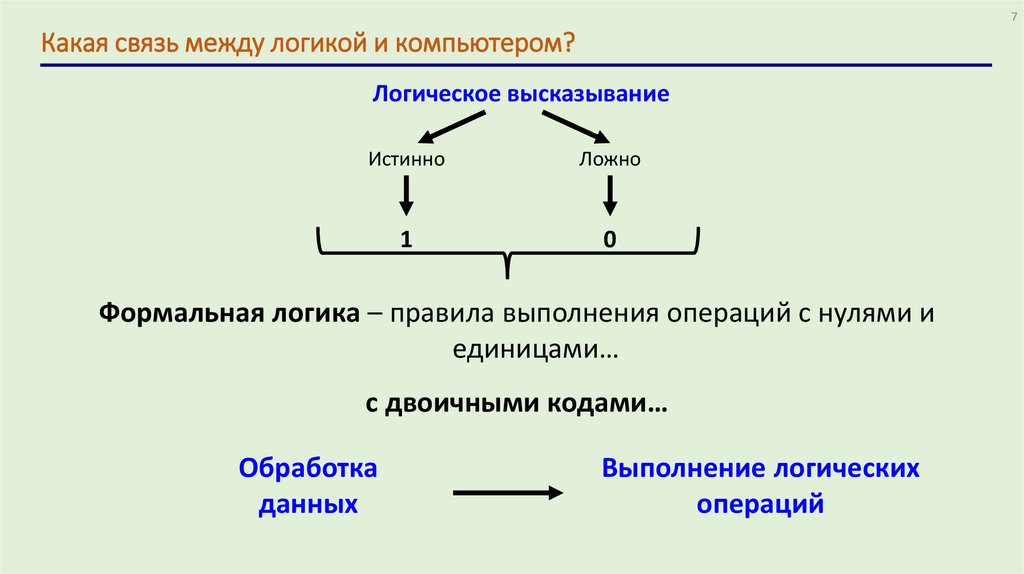
7
Какая связь между логикой и компьютером?
Логическое высказывание
Истинно
Ложно
1
0
Формальная логика – правила выполнения операций с нулями и
единицами…
с двоичными кодами…
Обработка
данных
Выполнение логических
операций

8.

Джордж Буль
(1815 - 1864)
Джордж Буль предложил
применить для исследования
логических высказываний
математические методы
(алгебра логики, алгебра
высказываний или булева
алгебра) .

9.

Используя правила алгебры логики, можно
строить запоминающие элементы в
компьютере и выполнять арифметические
действия.

10.

ЛОГИЧЕСКИЕ ОПЕРАЦИИ

11.

Так как мы не рассматриваем конкретное
содержание высказывания и нам важно
только, истинно оно или ложно, то
высказывание можно представить как
переменную, значением которой может
быть только 0 или 1.

12.

Существуют разные варианты
обозначения истинности и ложности
логических переменных:
Истина
И
True
T
1
Ложь
Л
False
F
0

13.

Простые высказывания назвали
логическими переменными, а сложные логическими функциями.
Для простоты записи высказывания
обозначаются латинскими буквами А, В, С.

14.

Сложные высказывания представляют собой
набор простых высказываний связанных
логическими операциями.

15.

С помощью логических переменных и символов
логических операций любое сложное
высказывание можно заменить логической
формулой (логическим выражением).

16.

Существует только три основных
логических операции, при помощи
которых можно записать любое
логическое выражение.

17.

«НЕ»
«И»
«ИЛИ»
инверсия
конъюнкция
дизъюнкция

18.

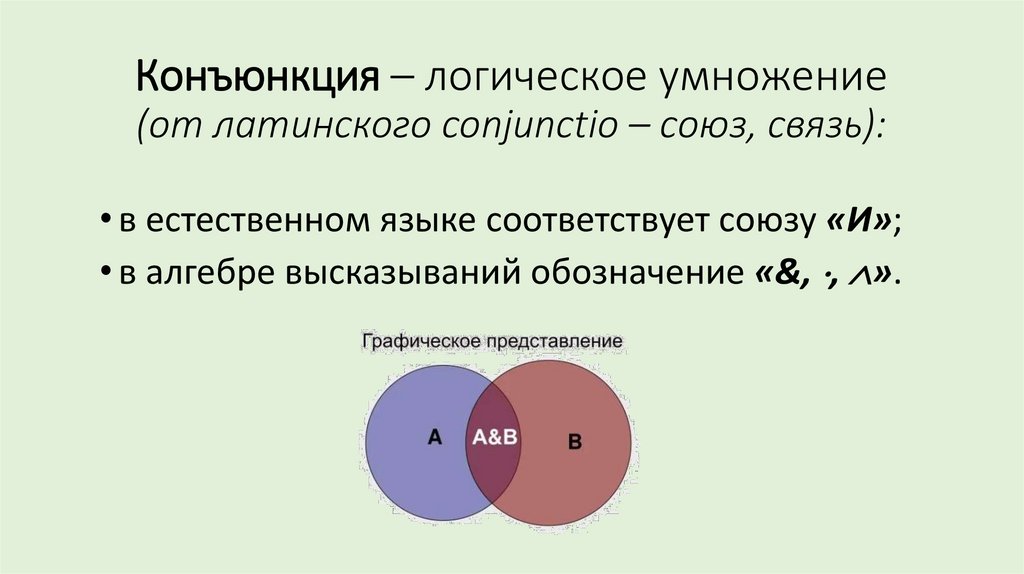
Конъюнкция – логическое умножение
(от латинского conjunctio – союз, связь):
• в естественном языке соответствует союзу «И»;
• в алгебре высказываний обозначение «&, , ».

19.

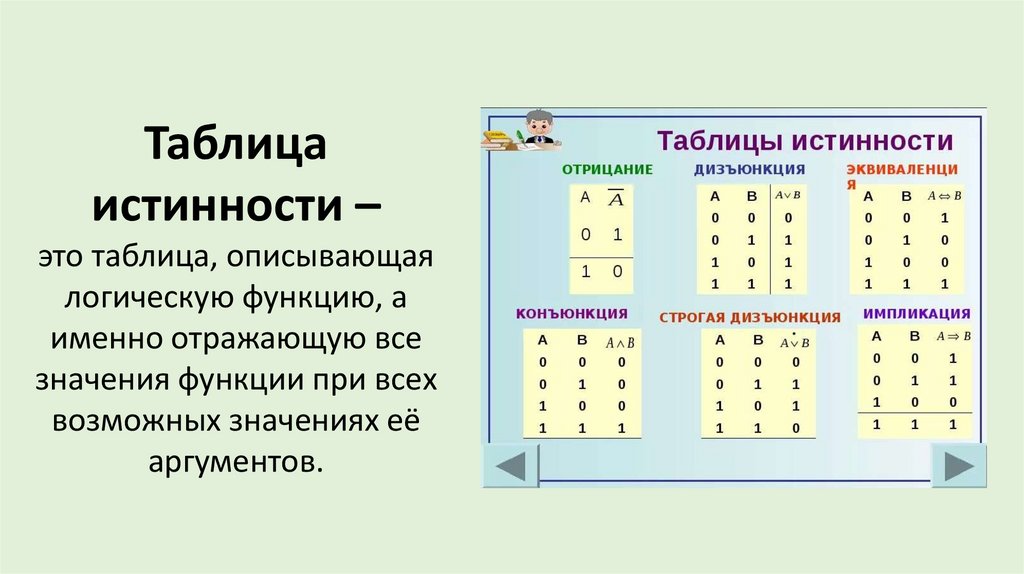
Таблица
истинности –
это таблица, описывающая
логическую функцию, а
именно отражающую все
значения функции при всех
возможных значениях её
аргументов.

20.

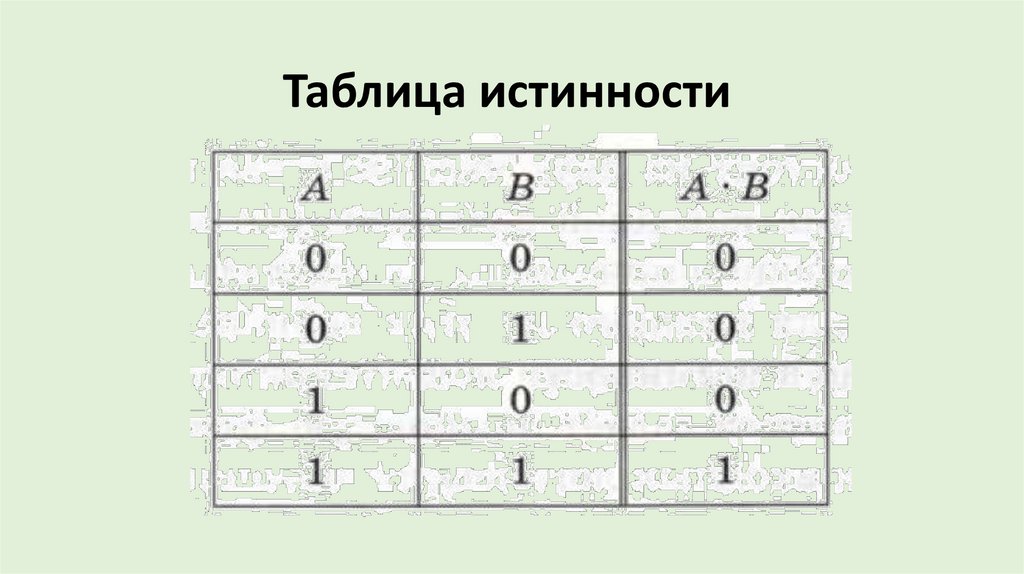
Таблица истинности

21.

Конъюнкция - это логическая операция,
ставящая в соответствие каждым двум простым
(или исходным) высказываниям составное
высказывание, являющееся истинным тогда и
только тогда, когда оба исходных высказывания
истинны, и ложным, когда хотя бы одно из
составляющих высказываний ложно.

22.

Москва – столица России И сегодня солнечно.

23.

Дизъюнкция - логическое сложение
(от латинского disjunctio - разобщение,
различие):
• в естественном языке соответствует союзу «ИЛИ»;
• в алгебре высказываний обозначение «V» или «+».

24.

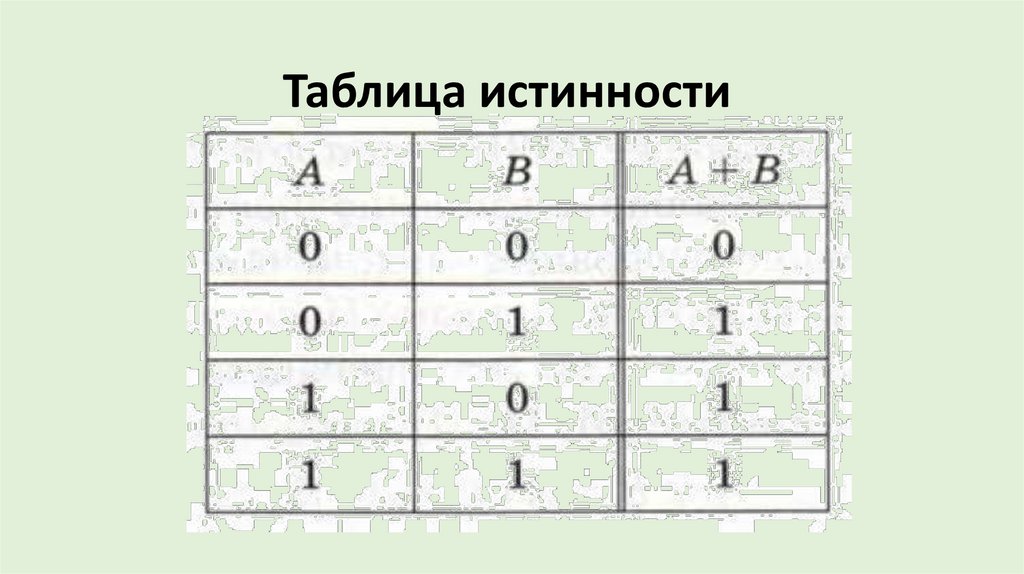
Таблица истинности

25.

Дизъюнкция - это логическая операция,
которая каждым двум простым (или исходным)
высказываниям ставит в соответствие составное
высказывание, являющееся ложным тогда и
только тогда, когда оба исходных высказывания
ложны, и истинным, когда хотя бы одно из
составляющих высказываний истинно.

26.

Париж – столица Франции ИЛИ сегодня пасмурно.

27.

Инверсия – логическое отрицание
(от латинского inversio — переворачивание,
перестановка):
• в естественном языке соответствует словам «неверно,
что...» и частице «не» ;
• в алгебре высказываний обозначение «¬» или «-».

28.

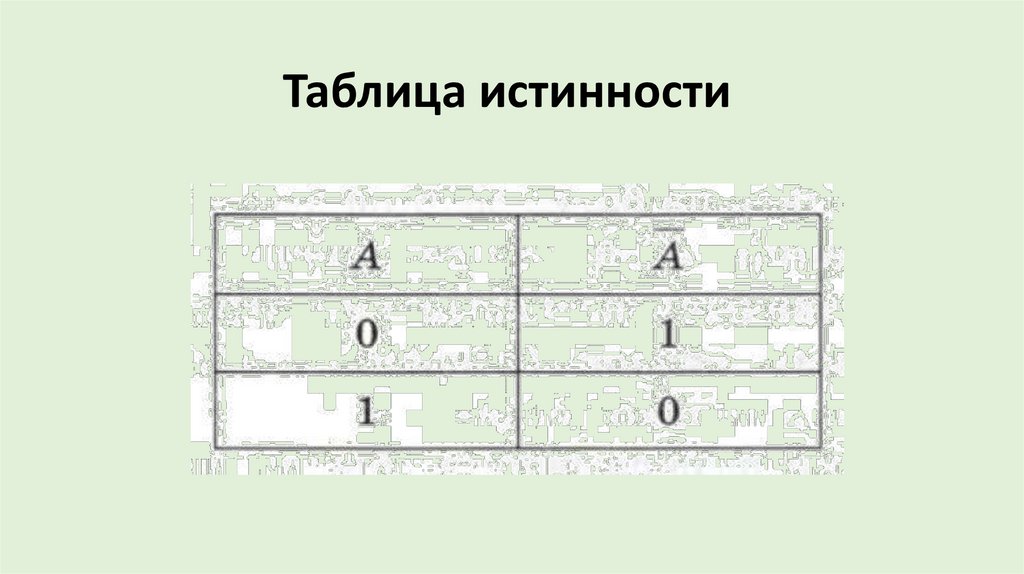
Таблица истинности

29.

Отрицание - логическая операция, которая
каждому исходному высказыванию ставит в
соответствие составное высказывание,
являющееся истинным, когда исходное
высказывание ложно, и ложным, когда
исходное высказывание истинно.

30.

Импликация – логическое следование
(от латинского implico — тесно
связываю):

31.

Таблица истинности

32.

ЕСЛИ На улице дождь, ТО асфальт мокрый.

33.

Эквиваленция – логическое тождество
(равнозначность, взаимная
обусловленность):

34.

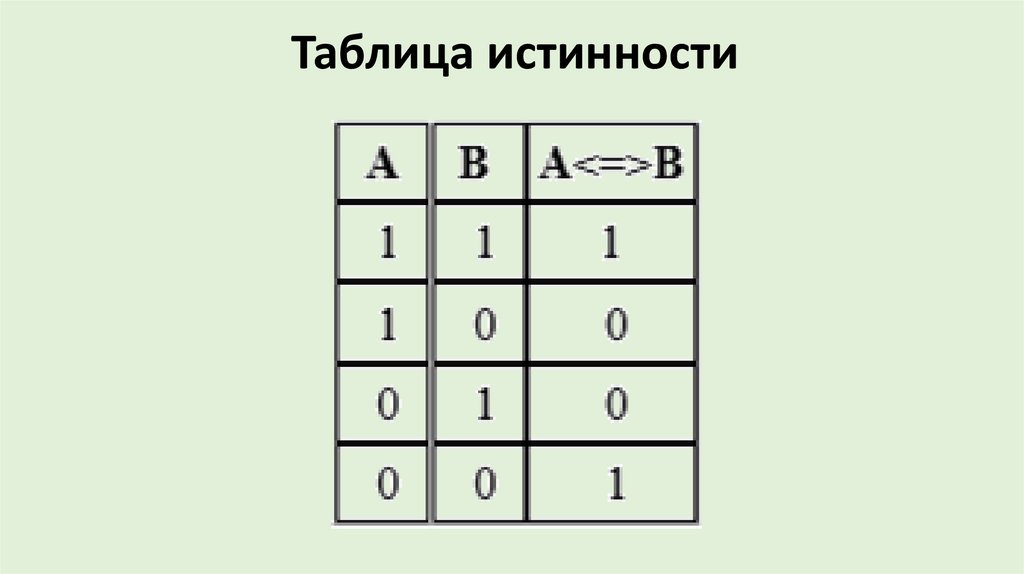
Таблица истинности

35.

Я сдам зачёт по информатике ТОГДА И
ТОЛЬКО ТОГДА, КОГДА сдам все
практические.

36.

37.

Порядок выполнения логических операций