Похожие презентации:
Предел функции
1.
Предел функции–
одно
из
основных
понятий
математического анализа. Понятие предела использовалось
еще Ньютоном во второй половине XVII века и математиками
XVIII века, такими как Эйлер и Лагранж, однако они понимали
предел интуитивно. Первые строгие определения предела дали
Больцано в 1816 году и Коши в 1821 году.
2.
Рассмотрим функции, графикикоторых изображены на следующих
рисунках:
y f (x)
y f (x)
y f (x)
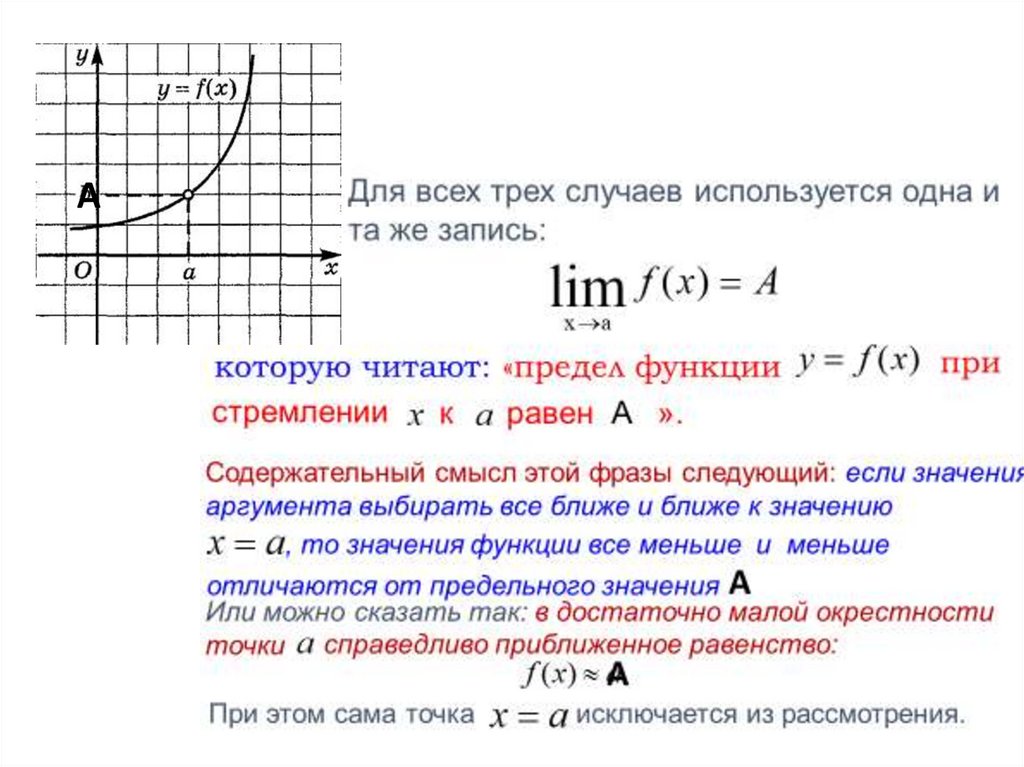
Во всех трех случаях изображена одна и та же кривая, но все
же изображают они три разные функции, отличающиеся друг
от друга своим поведением в точке
x a .
Рассмотрим каждый из этих графиков подробнее:
3.
Случай 1.lim f ( x) A
А
x a
f (a ) не существует
4.
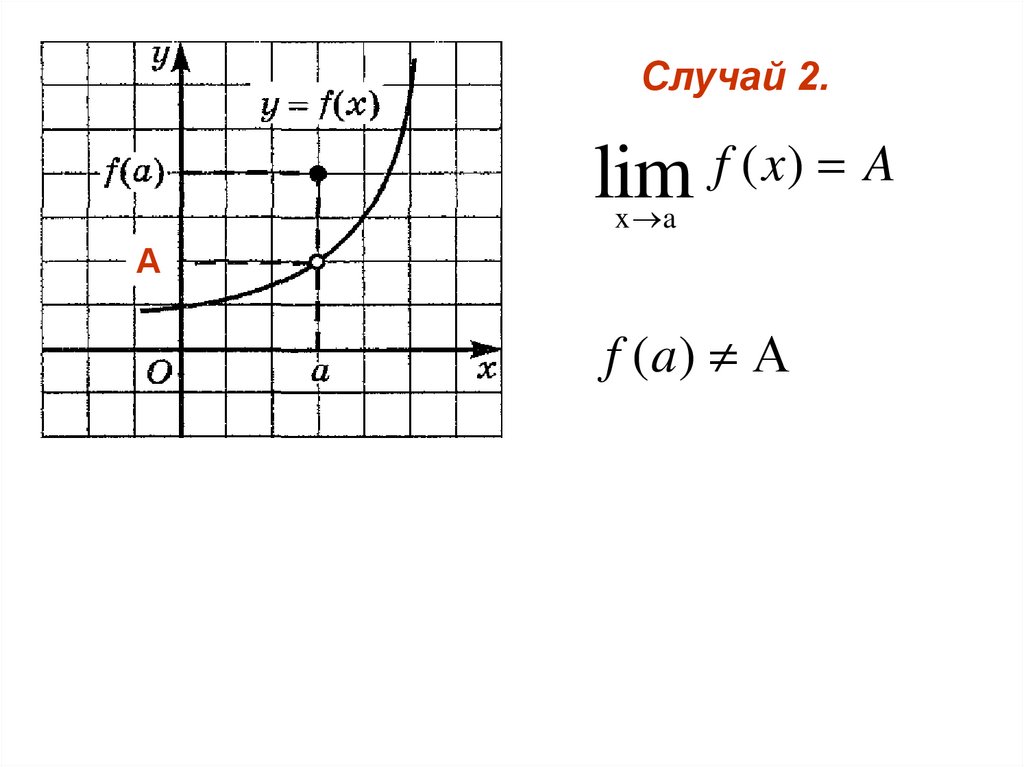
Случай 2.lim f ( x) A
x a
А
f (a) А
5.
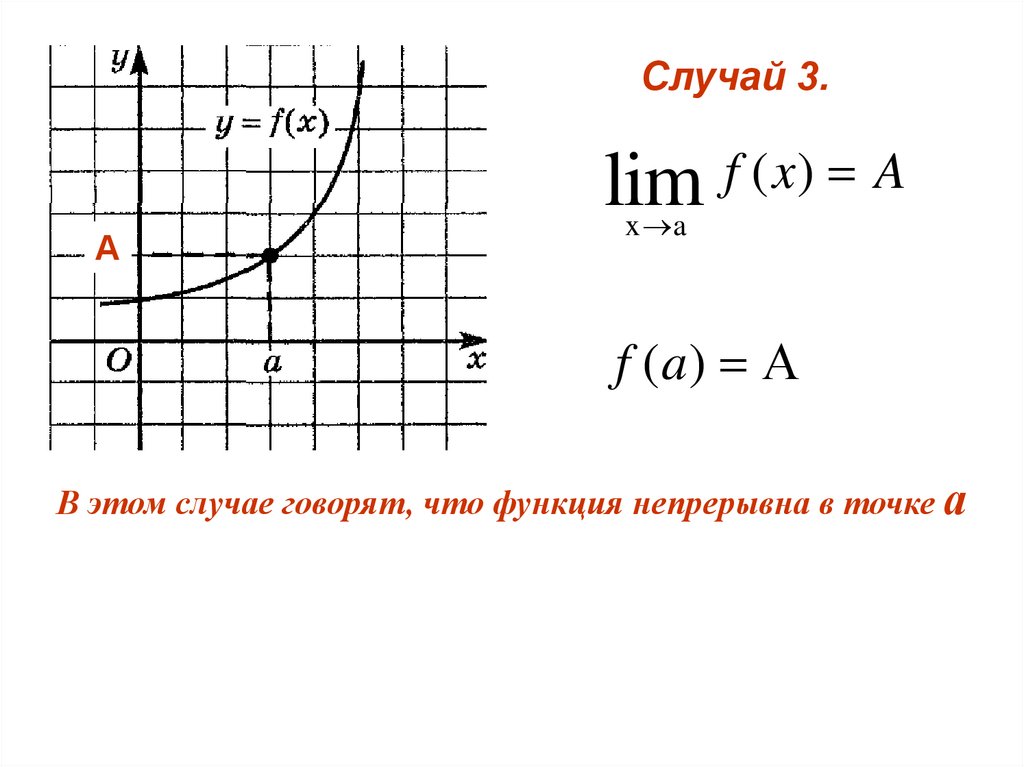
Случай 3.lim f ( x) A
А
x a
f (a) А
В этом случае говорят, что функция непрерывна в точке а
6.
A7.
Предел функции в точке0; 0; x : x x0 f ( x ) A
ε окрестность точки А
y
2
А
0
х0
х
δ окрестность точки x0
Геометрический смысл предела: для всех х из δ –
окрестности точки x0 точки графика функции лежат
внутри полосы, шириной 2ε, ограниченной прямыми: у
=А+ε,у=А-ε.
8.
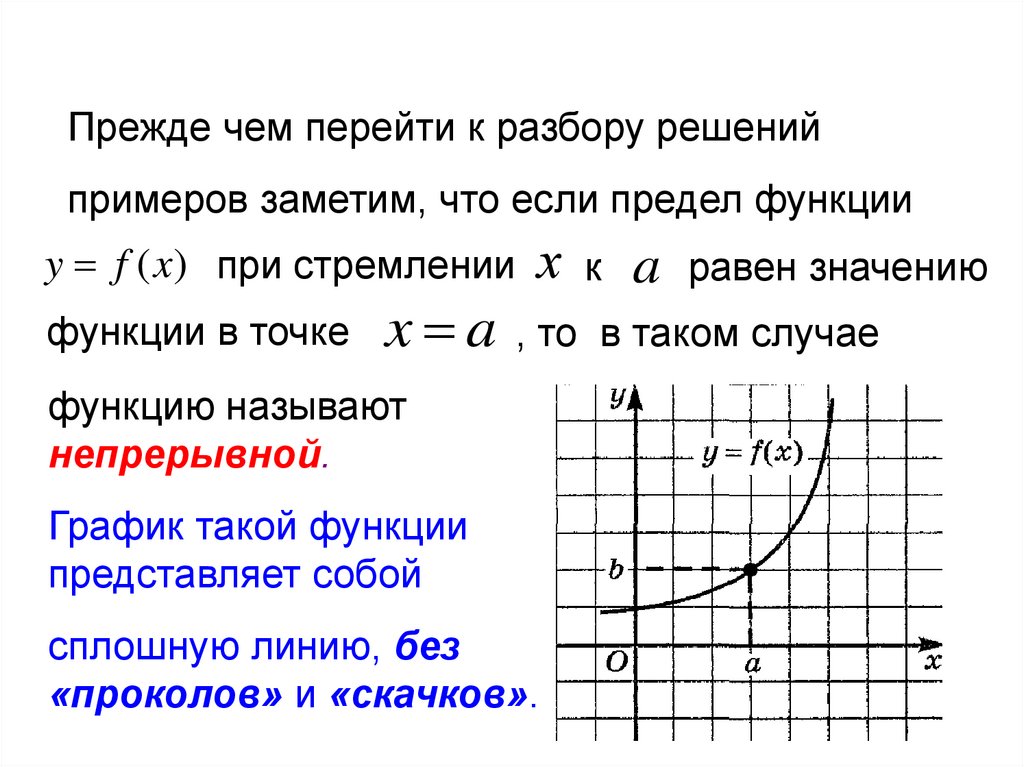
Прежде чем перейти к разбору решенийпримеров заметим, что если предел функции
y f (x) при стремлении
функции в точке
x a
х
к
a
равен значению
, то в таком случае
функцию называют
непрерывной.
График такой функции
представляет собой
сплошную линию, без
«проколов» и «скачков».
9.
Функцию y f (x) называют непрерывнойна промежутке X , если она непрерывна в
каждой точке этого промежутка.
Примерами непрерывных функций на всей числовой
прямой являются: y C ,
y kx b,
y ax 2 by c,
y | x |,
y x n , n ,
Функция y x непрерывна на луче [0, ),
функция y x n , n
непрерывна на промежутках ( , 0) (0, ).
10.
ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕЧисло b называется пределом функции в
точке а, если для всех значений х ,
достаточно близких к а и отличных от а,
значение функции f (x) сколь угодно мало
отличается
от b.
Если функция f (x) имеет предел в точке х,
то этот предел единственный.
lim f ( x ) b
x a
11.
1х
• х →0
lim f ( x)
x a
х
1
у 0
х
11
12.
Вычислениепредела:
lim f ( x ) A
x x0
начинают с подстановки предельного значения x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому числу.
3x 1 3 1 1 2
lim
2
2
x 1
1
x
Если при подстановки предельного
значения x0 в функцию f(x) получаются
выражения вида:
то предел будет равен:
C
0
C
0
13.
ПримерыВычислите:
.
14.
lim ( f ( x) g ( x)) lim f ( x) lim g ( x)x x0
x x0
x x0
15.
lim C Cx x0
16.
lim ( f ( x) g ( x)) lim f ( x) lim g ( x)x x0
x x0
x x0
17.
lim f ( x)f ( x) x x0
lim
, если _ lim g ( x) 0
x x0 g ( x)
x x0
lim g ( x)
x x0
18.
lim (k f ( x)) k lim f ( x)x x0
x x0
19.
lim ( z ) (lim z)n
x a
x a
n
20.
Часто при подстановке предельного значения x0 в функциюf(x) получаются выражения следующих видов:
0
;
0
;
Эти выражения называются
а
вычисление пределов в этом случае называется
.
21.
достаточно числитель и знаменатель дроби разделитьна множители, и затем сократить на множитель,
приводящий к неопределенности.
.
22.
Раскрытие неопределенностейРаскрытие неопределенности
0
0
x 2 14 x 32
0
x 2 x 16
lim 2
lim
x 2
x 2
x 6x 8
0
x 2 x 4
x 16 18
lim
9
x 2
x 4
2
Если f(x) – дробно –
рациональная
x 1 1 x 1 1
0
x 1 1 функция,
наlim Если f(x) – иррациональная
lim необходимо разложить
x 0
0
множители
числитель
иx 0 дробь, x
x
x 1 умножить
1
необходимо
знаменатель дроби
числитель и знаменатель
x 1 1
1дроби на выражение,
1
lim
lim
числителю.
x 0
x 0
сопряженное
x x 1 1
x 1 1 2
23.
Вычислитеx3 1
lim 2
x 1 x 1
x 3 3x 1
lim
1
x 0
x 4
x 5 x 10
lim
x 5
x 2 25
4 x 3 3x 2
lim
x 0 2 x 2 5
1 x
lim
x 0 1 2 x 2
2x3 2x 2
lim 3
x 0 5 x 4 x 2
2
2
lim 2 x 3x 4
2
x 2
x 3
lim 2
x 3 x 9
lim
x 4
x 1
2 x 2 x 15
lim
x 3 3 x 2 5 x 12
x 2 6x 5
lim
x 5
x 2 25
lim 7 x 2 4 x 3 5 x 1
x 1
x 1
24.
25.
Односторонние пределыВ определении предела функции
lim f ( x ) A
x x0
предполагается, что x стремится к x0 любым способом: оставаясь
меньше, чем x0 (слева от x0), большим, чем x0 (справа от x0), или
колеблясь около точки x0.
Бывают случаи, когда способ приближения аргумента x к x0 существенно
влияет на значение предела, поэтому вводят понятия односторонних
пределов.
Число А1 называют пределом функции слева в точке x0, если для любого
ε > 0 найдется такое δ >0, что для всех x ( x0 ; x0 ) справедливо
неравенство:
f ( x ) A1
Предел слева записывают так:
lim f ( x) A1
x x0 0
26.
Односторонние пределыЧисло А2 называют пределом функции справа в точке x0, если
0; 0; x x0 ; x0 f ( x ) A2
Предел справа записывают так:
Пределы функции слева и справа
называют односторонними
пределами.
y
А2
А1=А2=А
А1
0
lim f ( x ) A2
x x0 0
Очевидно, если существует
х0
х
lim f ( x ) A
x x0
то существуют и оба
односторонних предела, причем
А = А1 = А2



















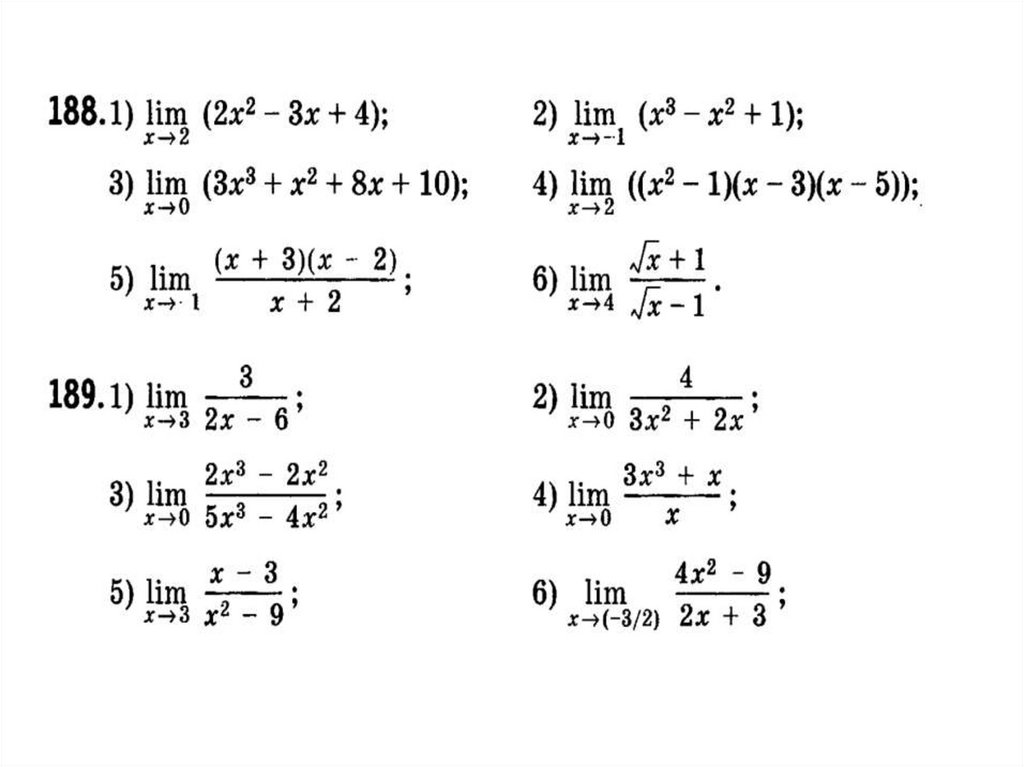


 Математика
Математика








