Похожие презентации:
Механические колебания по характеру физических процессов в системе
1. Механические колебания
2.
Механические колебания – это движения,которые точно или приблизительно
повторяются через определенные
интервалы времени.
3.
По характеру физических процессов всистеме, которые вызывают колебательные
движения, различают три основных вида
колебаний:
свободные
вынужденные
автоколебания
4.
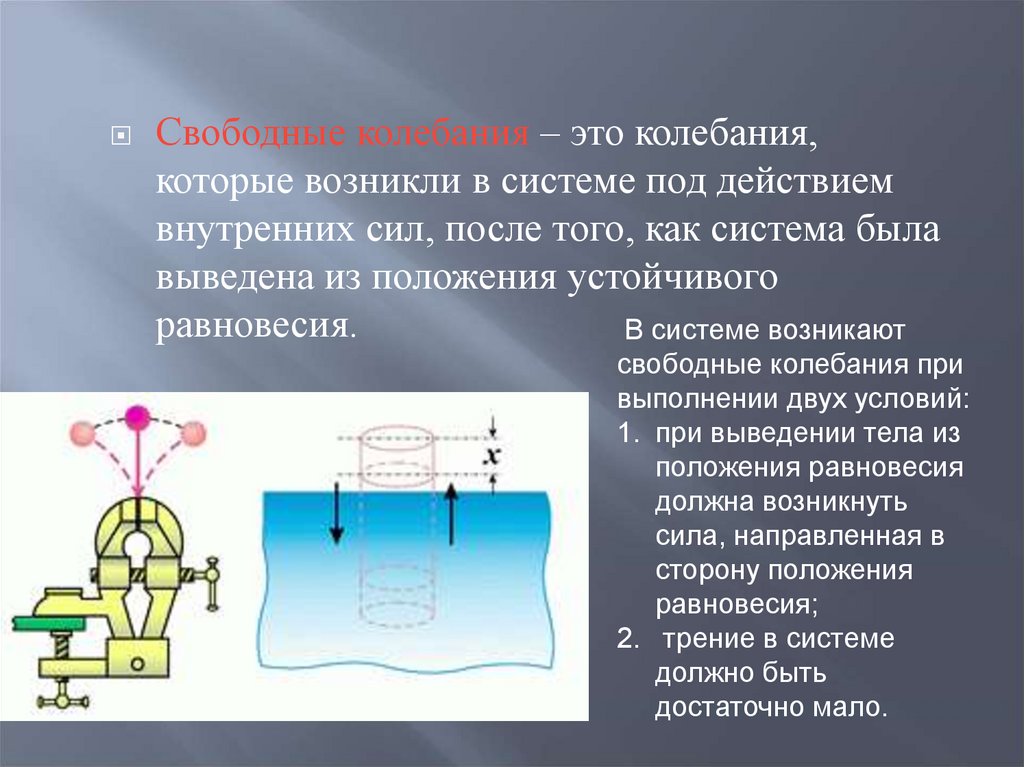
Свободные колебания – это колебания,которые возникли в системе под действием
внутренних сил, после того, как система была
выведена из положения устойчивого
равновесия.
В системе возникают
свободные колебания при
выполнении двух условий:
1. при выведении тела из
положения равновесия
должна возникнуть
сила, направленная в
сторону положения
равновесия;
2. трение в системе
должно быть
достаточно мало.
5.
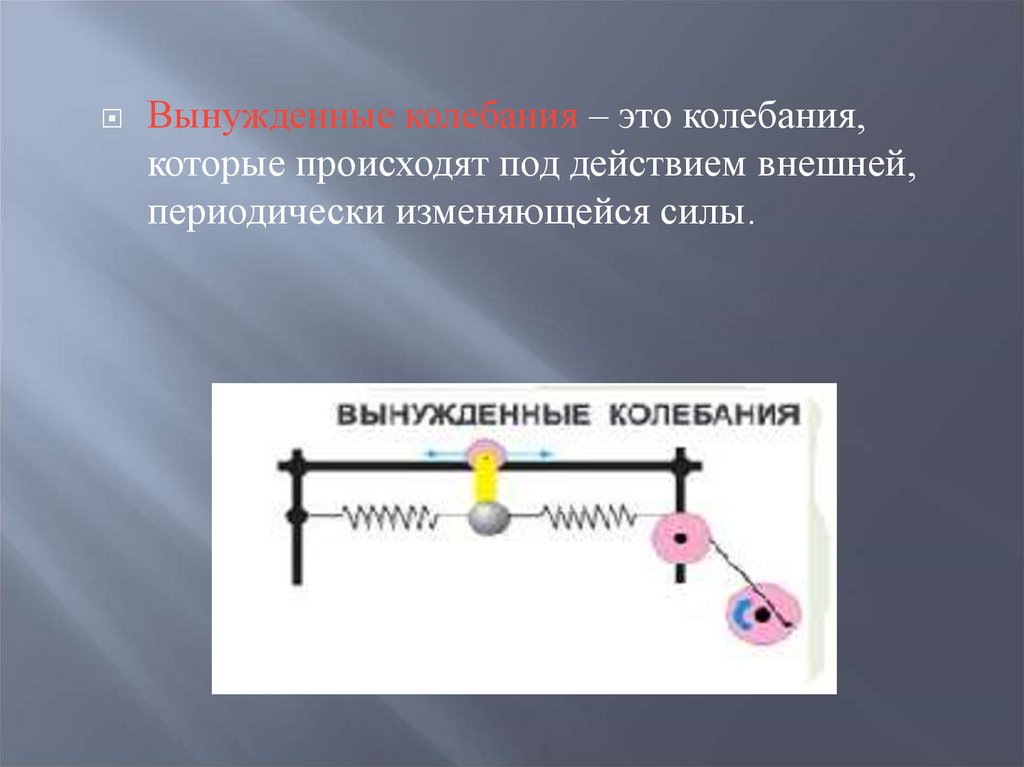
Вынужденные колебания – это колебания,которые происходят под действием внешней,
периодически изменяющейся силы.
6.
Маятниковые часыАвтоколебаниями
называются
незатухающие
колебания, которые
могут существовать в
системе без
воздействия на неё
внешних
периодических сил.
Часы с балансиром.
Спусковой механизм
часов:
1 — балансир;
2 — анкерная вилка;
3 — спусковое колесо
7. Уравнение движение груза, подвешенного на пружине
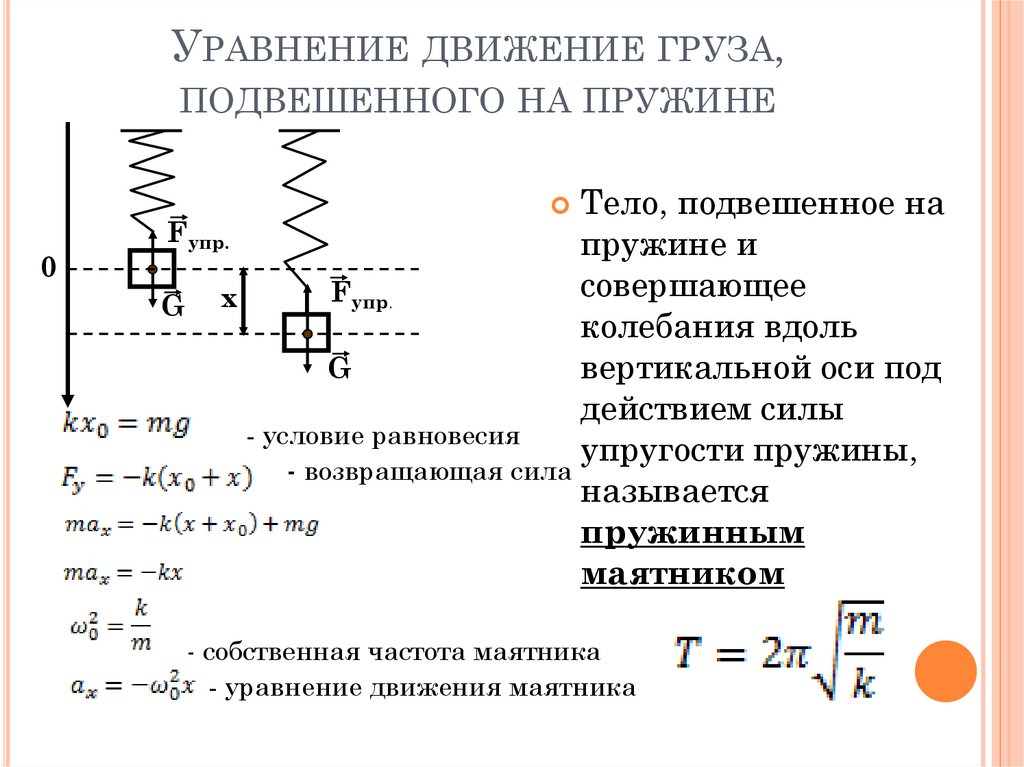
УРАВНЕНИЕ ДВИЖЕНИЕ ГРУЗА,ПОДВЕШЕННОГО НА ПРУЖИНЕ
0
Fупр.
G
Тело, подвешенное на
пружине и
совершающее
Fупр.
x
колебания вдоль
G
вертикальной оси под
действием силы
- условие равновесия
упругости пружины,
- возвращающая сила
называется
пружинным
маятником
- собственная частота маятника
- уравнение движения маятника
8. Уравнение движения математического маятника
УРАВНЕНИЕ ДВИЖЕНИЯМАТЕМАТИЧЕСКОГО МАЯТНИКА
При малых углах
Математический
маятник подвешенный на
тонкой невесомой нити
груз, размерами
которого можно
пренебречь по
сравнению с размерами
нити.
s – длина дуги, l - длина
маятника
Уравнение движения математического
маятника
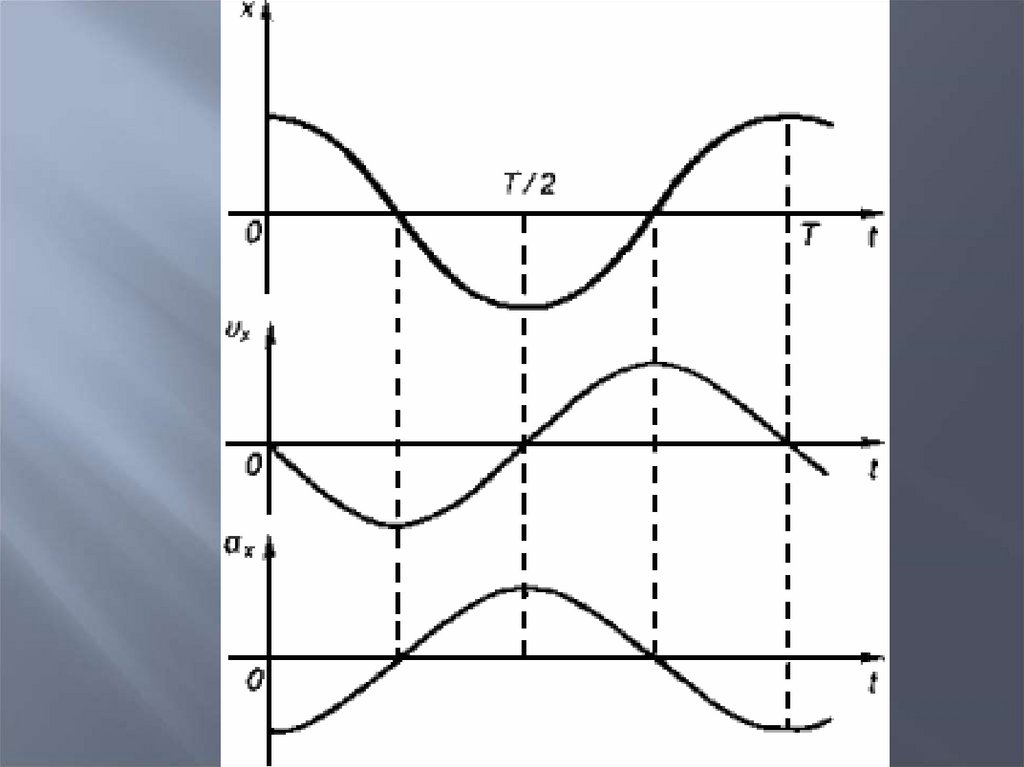
9.
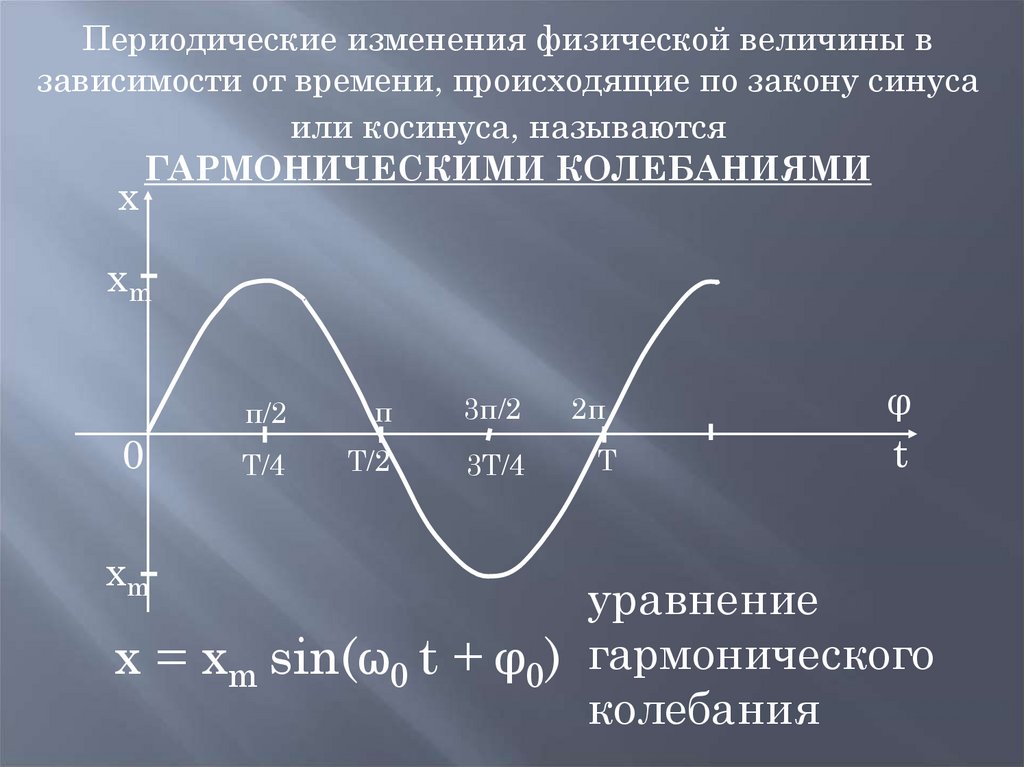
Периодические изменения физической величины взависимости от времени, происходящие по закону синуса
или косинуса, называются
ГАРМОНИЧЕСКИМИ КОЛЕБАНИЯМИ
x
xm
0
xm
π/2
π
3π/2
2π
T/4
T/2
3T/4
T
φ
t
уравнение
x = xm sin(ω0 t + φ0) гармонического
колебания
10. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ
• xm – модуль максимального смещения точки отположения равновесия называется
амплитудой;
• Т – время одного полного колнбания
называется периодом;
Т = t/n, где n – число полных колебаний
• x – смещение точки от положения равновесия в
данный момент времени.
11.
• число колебаний в единицу времени называетсячастотой;
ѵ = 1/Т – линейная частота колебаний
ѵ = n/t
[ѵ] = 1/c = 1 Гц (Герц)
Ѡ0 =2π/Т – циклическая частота колебаний
[ѡ0] = рад/с
• φ – фаза колебаний, которая определяет
состояние колебательной системы в любой момент
времени;
φ = ѡ0t + φ0
[φ] = рад
12.
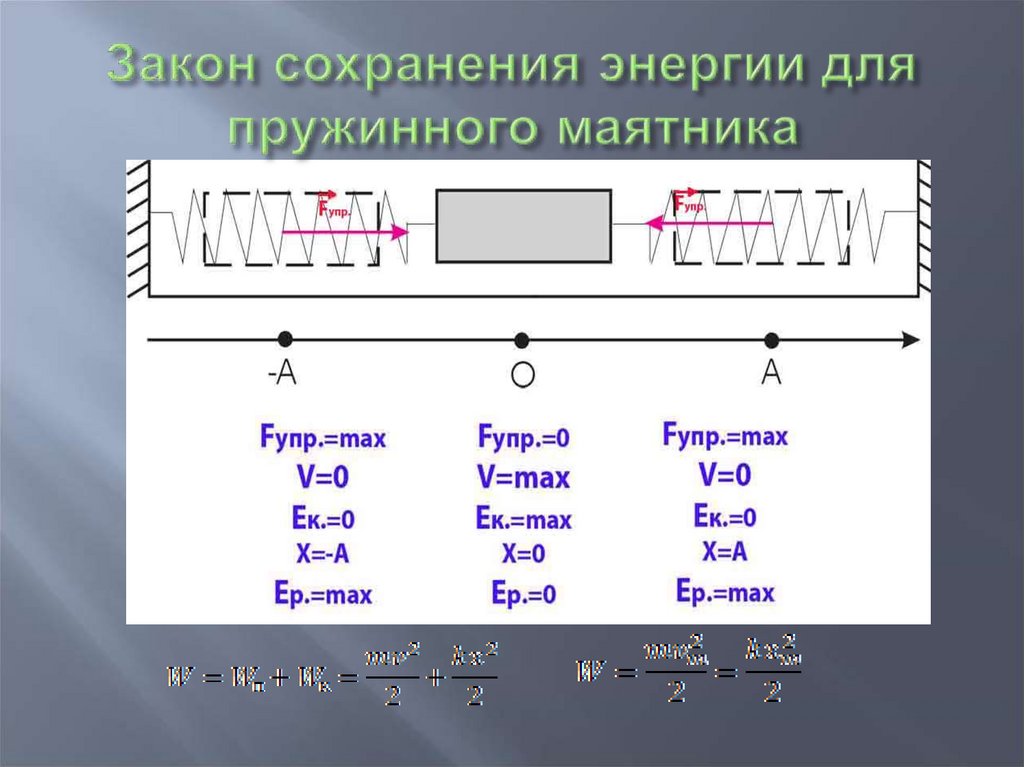
13. Закон сохранения энергии для пружинного маятника
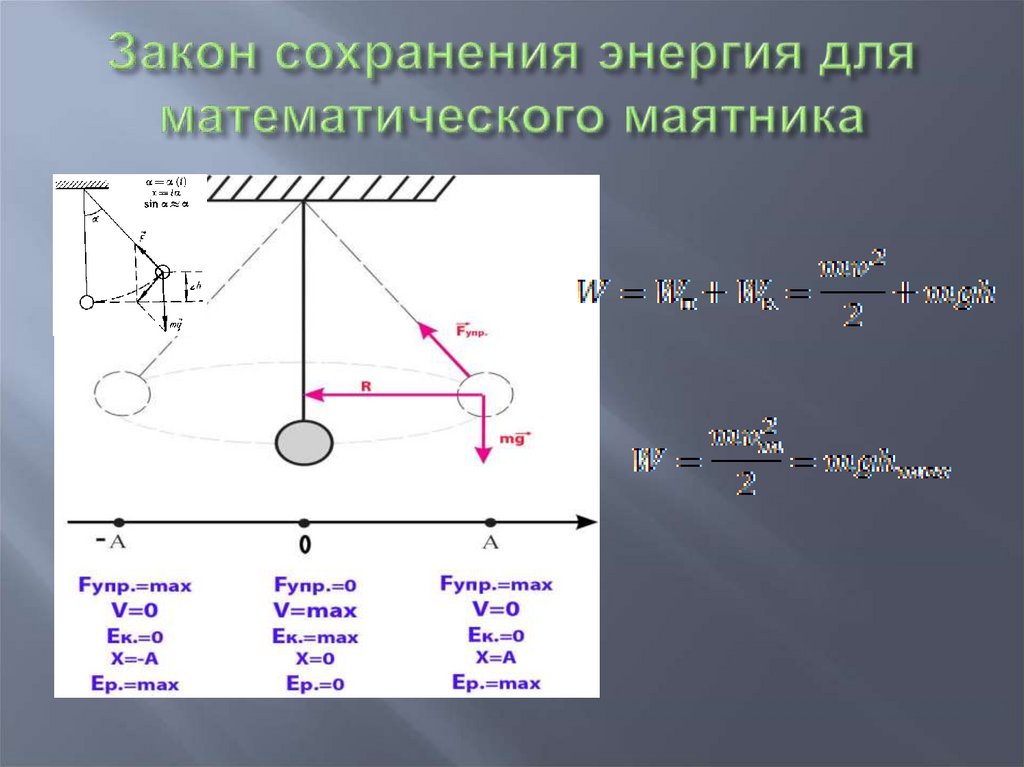
14. Закон сохранения энергия для математического маятника
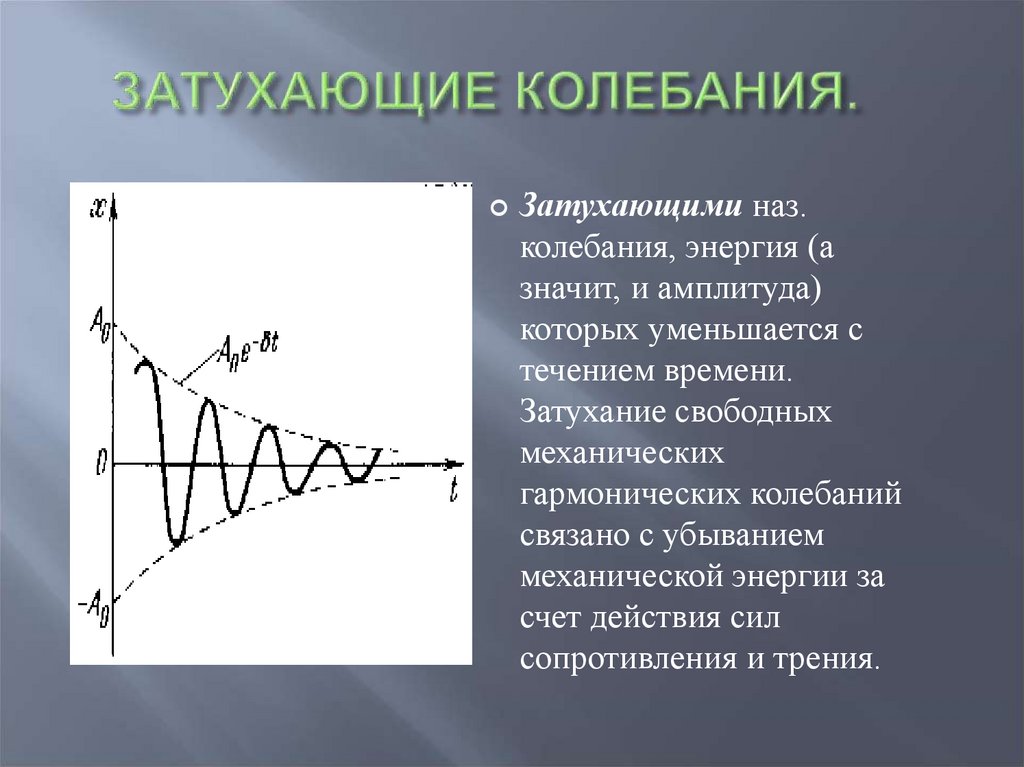
15. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ.
Затухающими наз.колебания, энергия (а
значит, и амплитуда)
которых уменьшается с
течением времени.
Затухание свободных
механических
гармонических колебаний
связано с убыванием
механической энергии за
счет действия сил
сопротивления и трения.
16.
17.
Резонанс – это резкое возрастаниеамплитуды вынужденных
колебаний.
Резонанс возникает только в том случае, когда
частота собственных колебаний совпадает с
частотой вынуждающей силы.
соб= вын








 Физика
Физика








