Похожие презентации:
О некоторых замечательных кривых. Циссоида. Диоклеса
1.
«О некоторыхзамечательных
кривых»
Доклады обучающихся
( к уроку « Функции ,их свойства и графики»)
2016г.
2.
ЦиссоидаДиоклеса
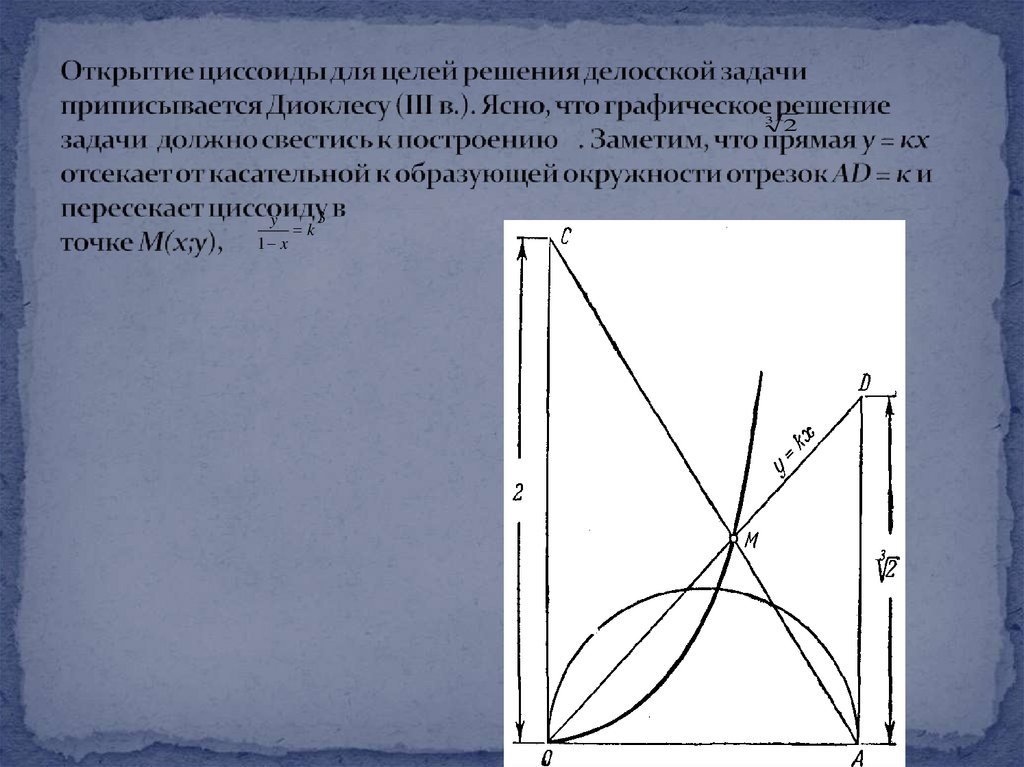
3.
4.
33
y
k
1 x
2
5.
Циклоиду можно определить кактраекторию точки, лежащей на окружности
круга единичного радиуса(производящего
круга),который без скольжения катится по
прямой(направляющей прямой)
6.
На направляющей горизонтальной прямой откладываютотрезок АА12 равной длине производящей окружности
радиуса r;
Строят производящую окружность радиуса r,там чтобы
направляющая прямая была касательной к ней в точке А;
Окружность и отрезок АА12 делят на несколько равных
частей, например на 12;
Из точек делений А1,А2…А12восстанавливаю
перпендикуляры до пересечения с продолжением
горизонтальной оси окружности в точках О1-О12;
Из точек деления окружности 1,2,…12 проводят
горизонтальные прямые на которых делают засечки дугами
окружности радиуса r;
Полученные точки А1,А2…А12 принадлежат циклоиде;
7.
8.
9.
x(t) = Asin(ωt + φ)Эту формулу называют законом (или
уравнением) гармонических
колебаний.
t – время, а х– отклонение
материальной точки от положения
равновесия
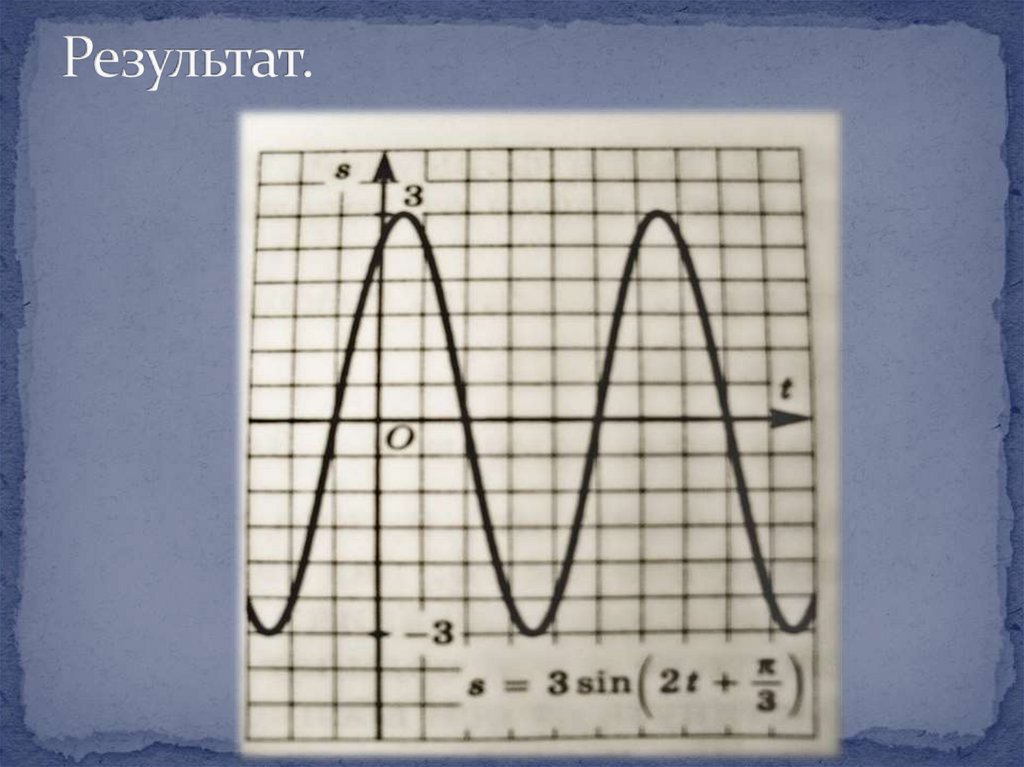
10.
11.
12.
Чтобы построить график такой функции,нужно над синусоидой S = sin t осуществить
следующие преобразования:
1) сжать её к оси ординат с коэффициентом 2;
2) растянуть от оси абсцисс с коэффициентом 3;
3) сжатую и растянутую полуволну сдвинуть
вдоль оси абсцисс
В результате получится полуволна искомого
графика, с помощью которой без труда можно
построить весь график
13.
14.
A – амплитуда колебаний (максимальноеотклонение от положения равновесия)
ω – частота колебаний
φ– начальная фаза колебаний
15.
16.
генератор гармонических колебанийпредназначен для применения в различных
радиотехнических устройствах с цифровым
управлением
17.
18.
19.
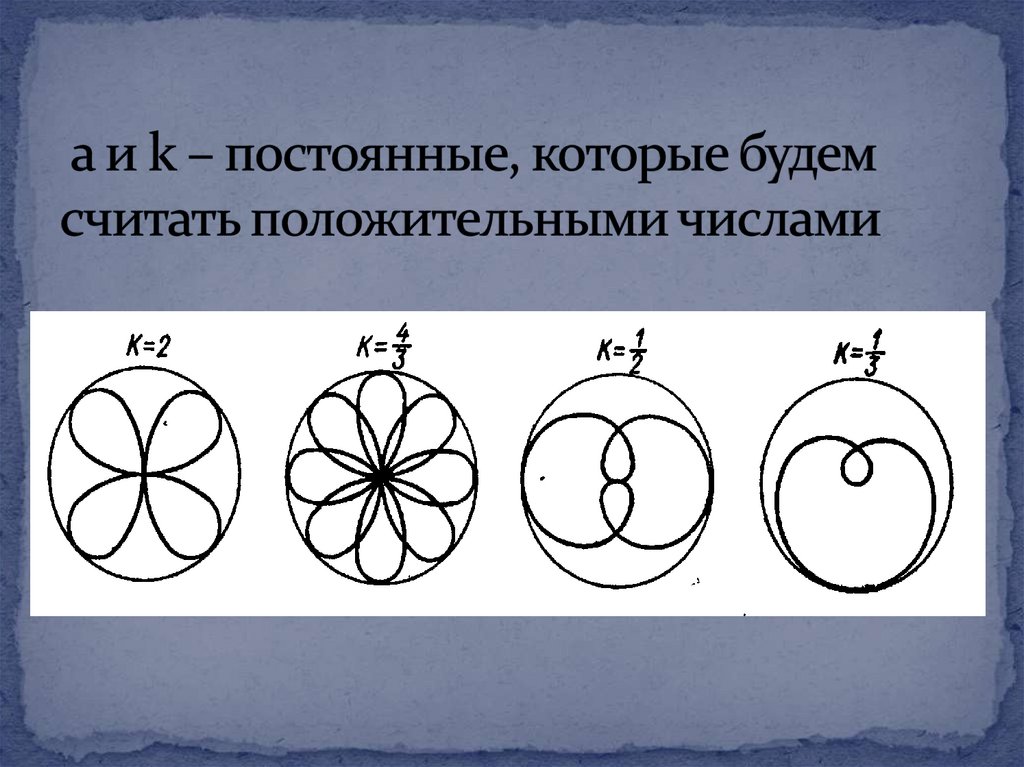
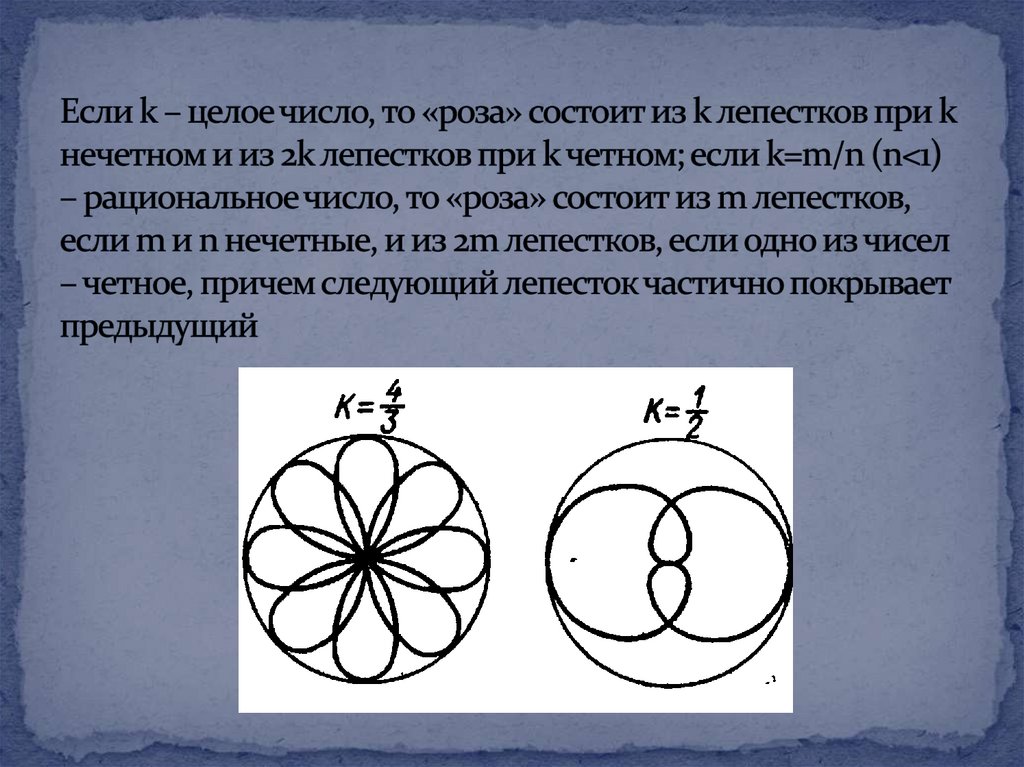
Обратимся к исследованию формы роз.Поскольку правая часть
уравнения не может превышать
величины a, то и вся роза, очевидно,
умещается внутри круга радиусом a.
Количество же лепестков розы зависит
от величины модуля k
20.
21.
Если модуль k – иррациональное число, то розасостоит из бесчисленного
множества лепестков, частично
накладывающихся друг на друга.
22.
23.
1 «Алгебра и начала анализа Самостоятельныеработы 10 класс»
Л.А
.Александрова изд. «Мнемозина» 2010г
2 «Алгебра и начала анализа 10-11 класс»
А. Г. Мордкович
изд.«Мнемозина» 2010г
«ЕГЭ Математика 2009»
Креславская О. А .изд.«Эксмо»
«ЕГЭ Математика 2003-2004»
Л. О. Денищева изд. «Просвещение»
Интернетресурсы.


















 Математика
Математика








