Некоторые замечательные кривые

1. Некоторые замечательные кривые

НЕКОТОРЫЕ
ЗАМЕЧАТЕЛЬНЫЕ
КРИВЫЕ
«Математика выявляет порядок, симметрию и
определенность, а это – важнейшие виды
прекрасного»
Аристотель

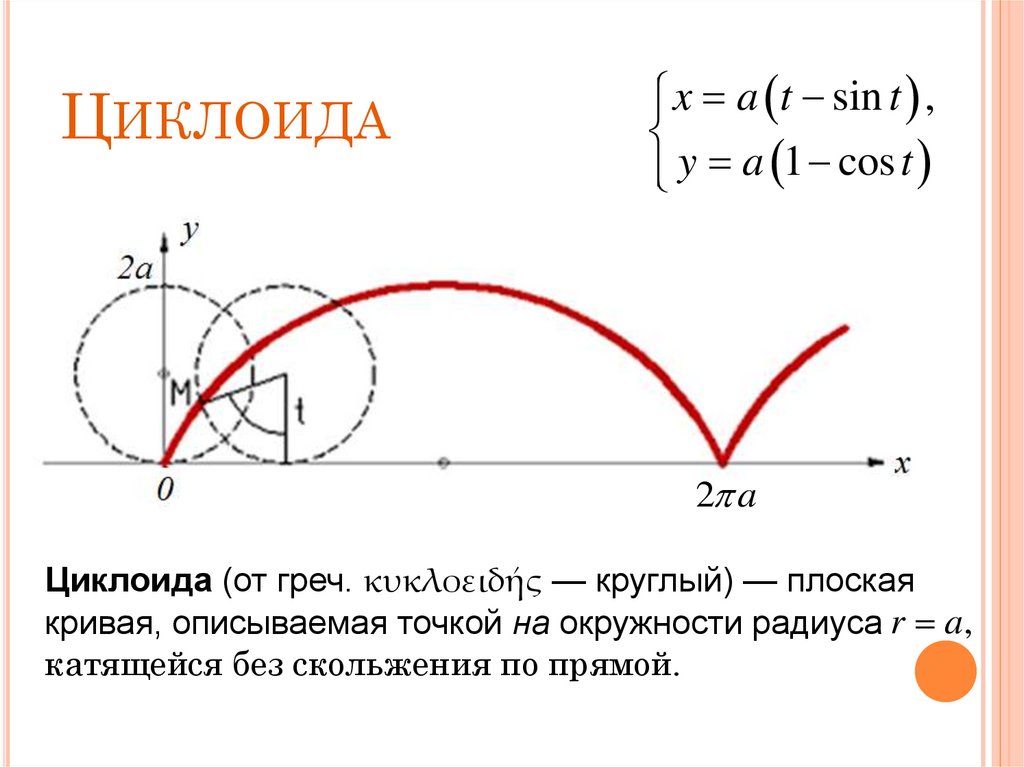
2. Циклоида

ЦИКЛОИДА
x a t sin t ,
y a 1 cos t
2 a
Циклоида (от греч. κυκλοειδής — круглый) — плоская
кривая, описываемая точкой на окружности радиуса r a,
катящейся без скольжения по прямой.

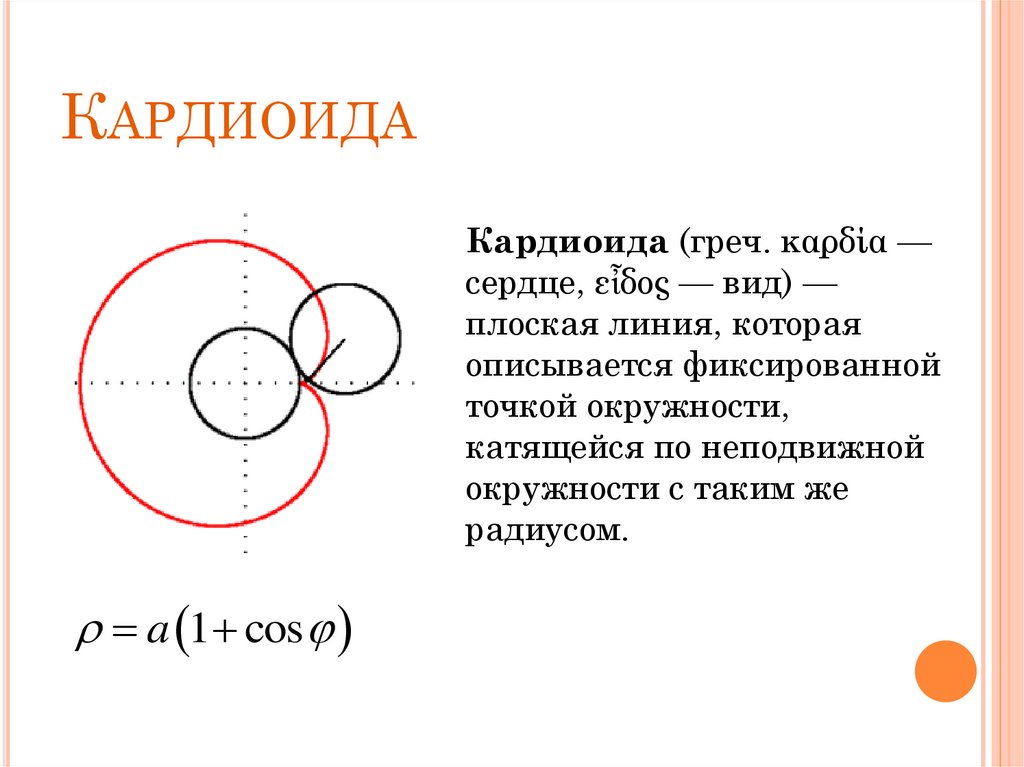
3. Кардиоида

КАРДИОИДА
Кардиоида (греч. καρδία —
сердце, εἶδος — вид) —
плоская линия, которая
описывается фиксированной
точкой окружности,
катящейся по неподвижной
окружности с таким же
радиусом.
a 1 cos

4. Астроида

.
АСТРОИДА
Астроида (от греч. αστρον звезда и ειδος - вид, то есть
звездообразная) — плоская
кривая, описываемая точкой
окружности радиуса r ,
катящейся по внутренней
стороне окружности радиуса R 4r
x a cos3 t ,
3
y
a
sin
t

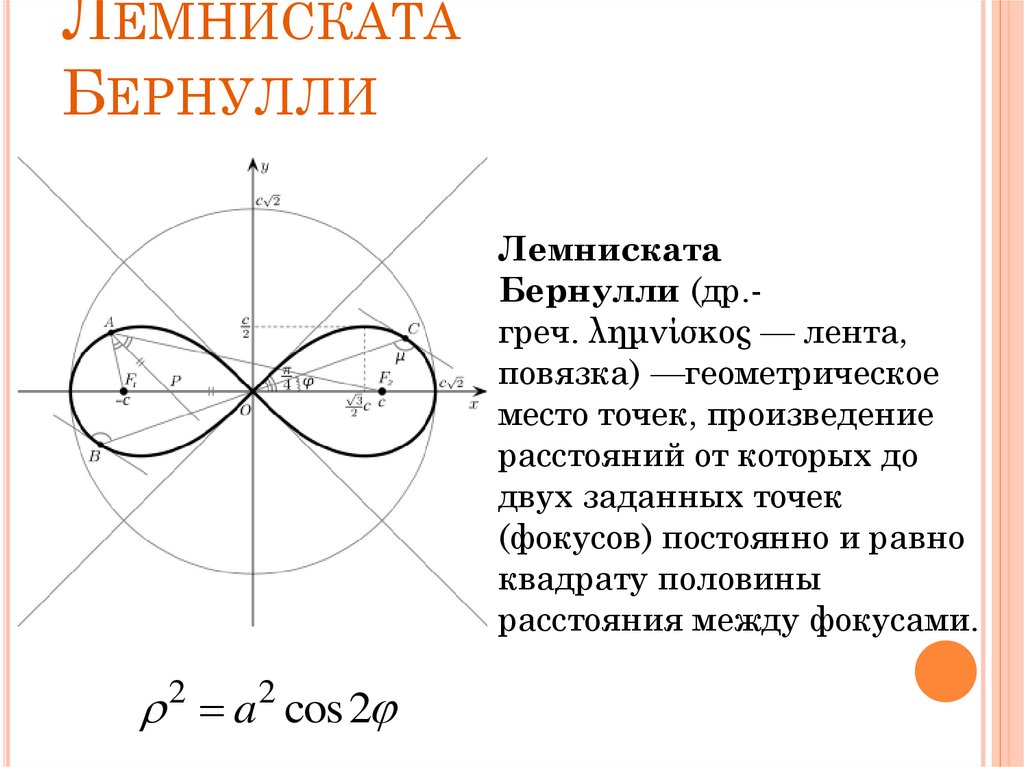
5. Лемниската Бернулли

ЛЕМНИСКАТА
БЕРНУЛЛИ
Лемниската
Бернулли (др.греч. λημνίσκος — лента,
повязка) —геометрическое
место точек, произведение
расстояний от которых до
двух заданных точек
(фокусов) постоянно и равно
квадрату половины
расстояния между фокусами.
2 a2 cos 2

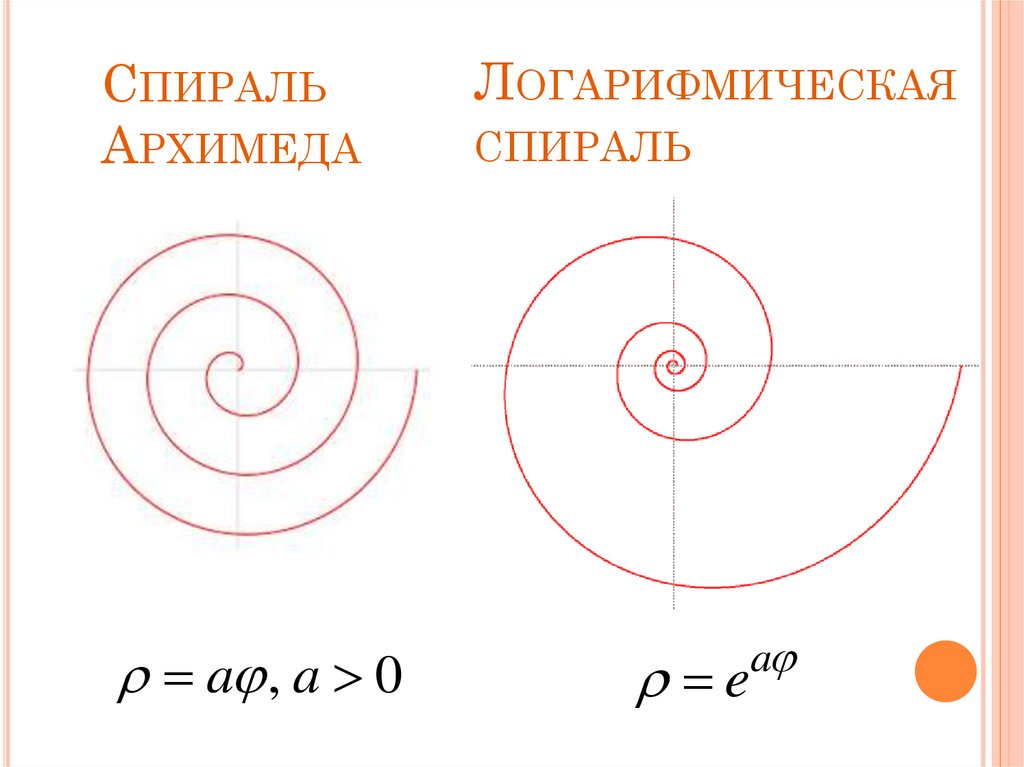
6. Спираль Архимеда

СПИРАЛЬ
АРХИМЕДА
a , a 0
ЛОГАРИФМИЧЕСКАЯ
СПИРАЛЬ
e
a

7. Цепная линия

ЦЕПНАЯ ЛИНИЯ
Цепная линия –
плоская кривая, форму
которой принимает
однородная гибкая
нерастяжимая тяжелая
нить, закрепленная на
концах и провисающая
под действием силы
тяжести.
x
x
a a
y e e a или
2
x
y ach
a

8. Цепная линия

ЦЕПНАЯ ЛИНИЯ

9. Цепная линия

ЦЕПНАЯ ЛИНИЯ

10. Цепная линия

ЦЕПНАЯ ЛИНИЯ

11. Кардиоида во фрактальном множестве Мандельброта занимает его центральную часть

КАРДИОИДА ВО ФРАКТАЛЬНОМ
МНОЖЕСТВЕ МАНДЕЛЬБРОТА ЗАНИМАЕТ
ЕГО ЦЕНТРАЛЬНУЮ ЧАСТЬ

12. Логарифмическая спираль в природе

ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ В
ПРИРОДЕ

13. Семена в цветке подсолнечника размещаются вдоль кривых, напоминающих спираль Ферма 

Спираль Ферма
СЕМЕНА
В
РАЗМЕЩАЮТСЯ
ЦВЕТКЕ
a
2
ПОДСОЛНЕЧНИКА
ВДОЛЬ
НАПОМИНАЮЩИХ СПИРАЛЬ
2
ФЕРМА
КРИВЫХ,

14.

«Инженер,
не
владеющий
математическими методами, - это не
инженер, а монтёр… Инженер в полном
смысле этого слова немыслим без знания
математики. Ничего нельзя сделать без
математики:
мост
построить
нельзя,
плотину – нельзя, гидростанцию – нельзя.»
Александр Данилович Александров