Сложение и вычитание дробей с разными знаменателями. Дипломная работа

1.

ДИПЛОМНАЯ РАБОТА
МЕТОДИКА ОБУЧЕНИЯ РЕШЕНИЮ
ИССЛЕДОВАТЕЛЬСКИХ ЗАДАЧ ПО ТЕМЕ
«СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С
РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ»
Выполнил:
Иванин Иван Викторович
студент 4 курса, 4 группы
очной формы обучения
Научный руководитель:
Малинникова Наталья Алексеевна
кандидат педагогических наук,
доцент

2.

Целью данной дипломной работы
является выявление особенностей
исследовательских заданий по теме:
«Сложение и вычитание дробей с
разными знаменателями».

3.

ЗАДАЧИ
1) Анализ научной литературы: сущность исследовательской деятельности
учащихся в процессе обучения математике; сущность исследовательского
задания, виды, методические приемы работы с исследовательским
заданием и т.д.;
2) Анализ математических заданий исследовательского характера по теме
«Сложение и вычитание дробей с разными знаменателями»;
3) Анализ школьных учебников с позиций возможности включения
учащихся в исследовательскую деятельность при изучении темы
«Сложение и вычитание дробей с разными знаменателями»;
4) Разработка методики работы с заданиями исследовательского характера
по теме «Сложение и вычитание дробей с разными знаменателями»;
5) Разработка дидактических материалов текстового и электронного
форматов: фрагменты уроков, электронные ресурсы, сопровождающие
фрагменты уроков.

4.

ГЛАВА 1. ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ МЕТОДИКИ
РЕШЕНИЯ ИССЛЕДОВАТЕЛЬСКИХ ЗАДАНИЙ ПО
МАТЕМАТИКЕ
§1. Сущность исследовательского задания
§2. Методика обучения решению исследовательских
заданий
§3. Логико-дидактический анализ темы «Сложение и
вычитание дробей с разными знаменателями»

5.

§1. СУЩНОСТЬ ИССЛЕДОВАТЕЛЬСКОГО
ЗАДАНИЯ
В данном параграфе были рассмотрены определения «исследовательского
задания» различных авторов ( У. С. Кисметова, Н. Г. Прокушева, И. Я.
Лернер, О. И. Федяев и др.).
Проанализировав данные определения можно выделить соответствующие
признаки исследовательского задания:
1.
Отсутствие алгоритма.
2.
Нестандартность формулировки проблемы.
3.
Нестандартность нахождения способов решения.
4.
Возможность составления новых заданий, вытекающих из решения
данной.
5.
Многовариантность гипотез.

6.

КЛАССИФИКАЦИЯ ИССЛЕДОВАТЕЛЬСКИХ
ЗАДАНИЙ
Ярков В. Г. классифицирует исследовательские задачи:
- задачи на существование математических объектов;
- задачи на сравнение математических понятий, на установление взаимосвязи между
математическими понятиями;
- задачи на доказательство;
- задачи на традиционное исследование;
- задачи на исследование математических предложений;
- задачи на обобщение и выделение частных случаев.
Л. М. Лоповок к задачам исследовательского характера относит следующие:
- задачи на моделирование;
- задачи с неполными данными условия;
- задачи на исследование;
- задачи, решения которых начинается исследованием;
- задачи на построение.

7.

При выполнении исследовательских задач на
уроках, можно считать, что на уроке
организована исследовательская
деятельность, так как она подразумевает
выполнение учащимися исследовательских
задач с заранее неизвестным решением,
направленных на создание представления об
объекте или окружающем мире.

8.

§2. МЕТОДИКА ОБУЧЕНИЯ РЕШЕНИЮ
ИССЛЕДОВАТЕЛЬСКИХ ЗАДАНИЙ
Этапы исследовательской деятельности
Этапы базовой методики
1.
Мотивация исследовательской
деятельности.
1. Анализ решения.
2.
Формулировка проблемы.
2. Поиск путей решения.
3.
Поиск путей решения проблемы:
3. Оформление решения.
а) сбор, систематизация и анализ
данных;
б) выдвижение гипотез;
в) проверка гипотез;
г) доказательство или опровержение
гипотез;
4. Реализация и проверка найденного
решения.
5.
Анализ полученных результатов и выводы.
4. Исследование задачи.

9.

ЭТАПЫ МЕТОДИКИ РЕШЕНИЯ
ИССЛЕДОВАТЕЛЬСКИХ ЗАДАНИЙ
1.
2.
3.
4.
5.
6.
Анализ условия.
Постановка проблемы.
Выдвижение гипотезы.
Проверка гипотезы.
Сбор материалов.
Выводы по решению задачи

10.

ДИДАКТИЧЕСКИЕ ПРИЕМЫ ПРИ РЕШЕНИИ
ИССЛЕДОВАТЕЛЬСКИХ ЗАДАНИЙ
• Прием использования таблицы;
• Прием использования заданий с пропусками;
• Прием использования диалоговых технологий

11.

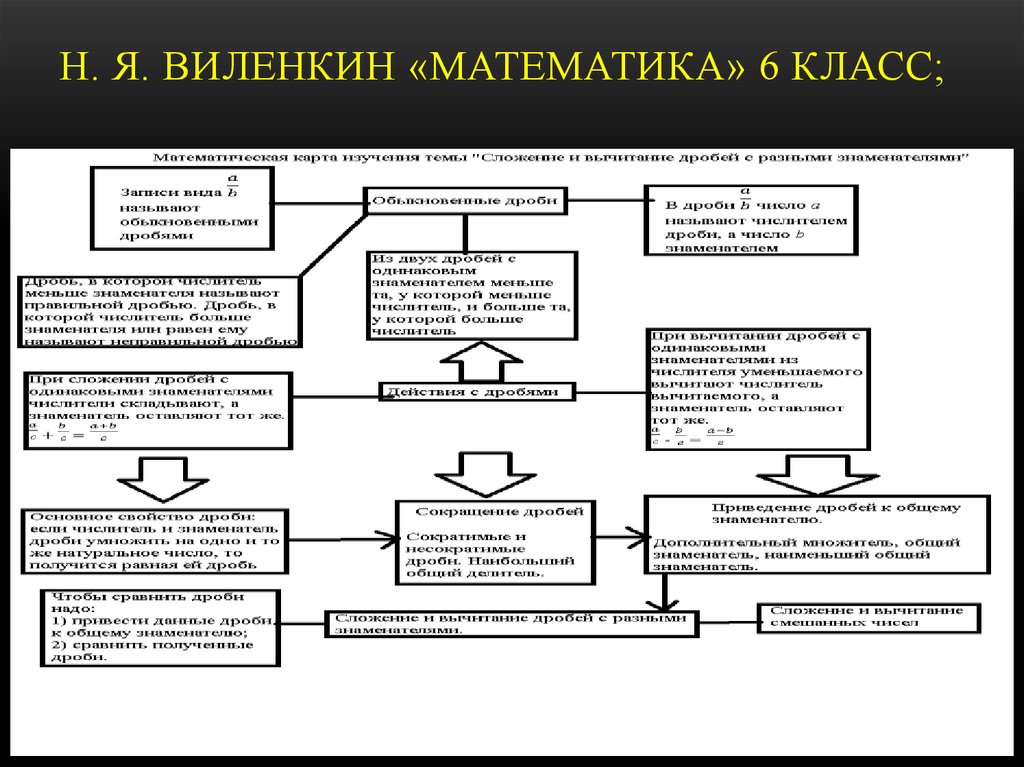
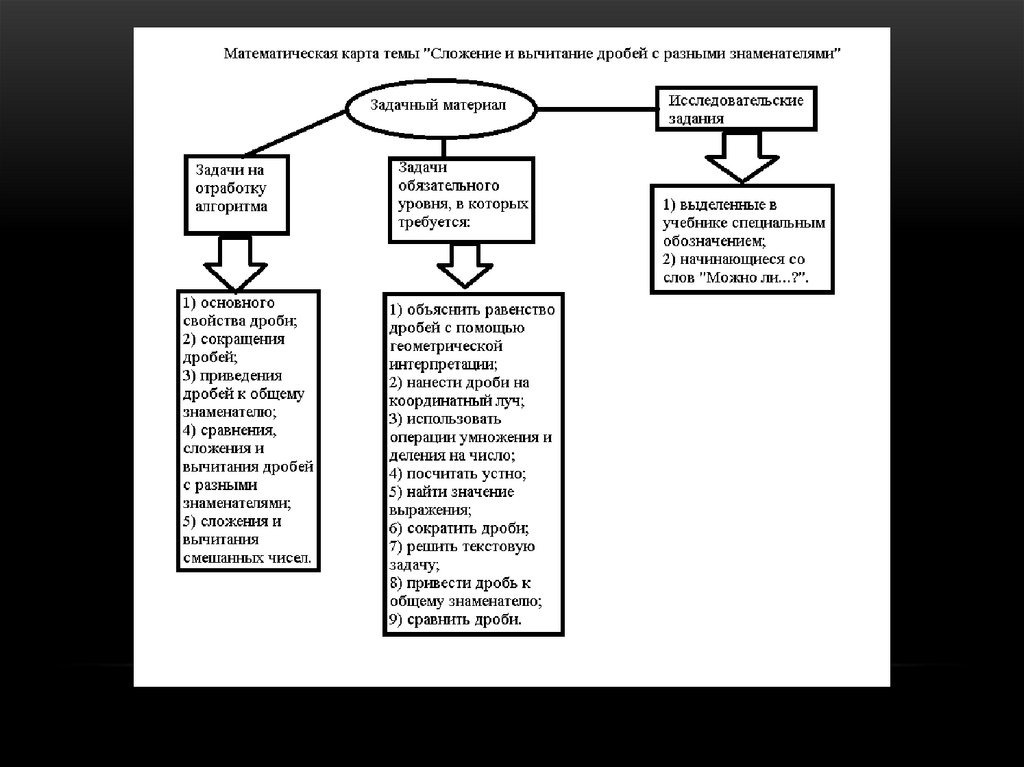
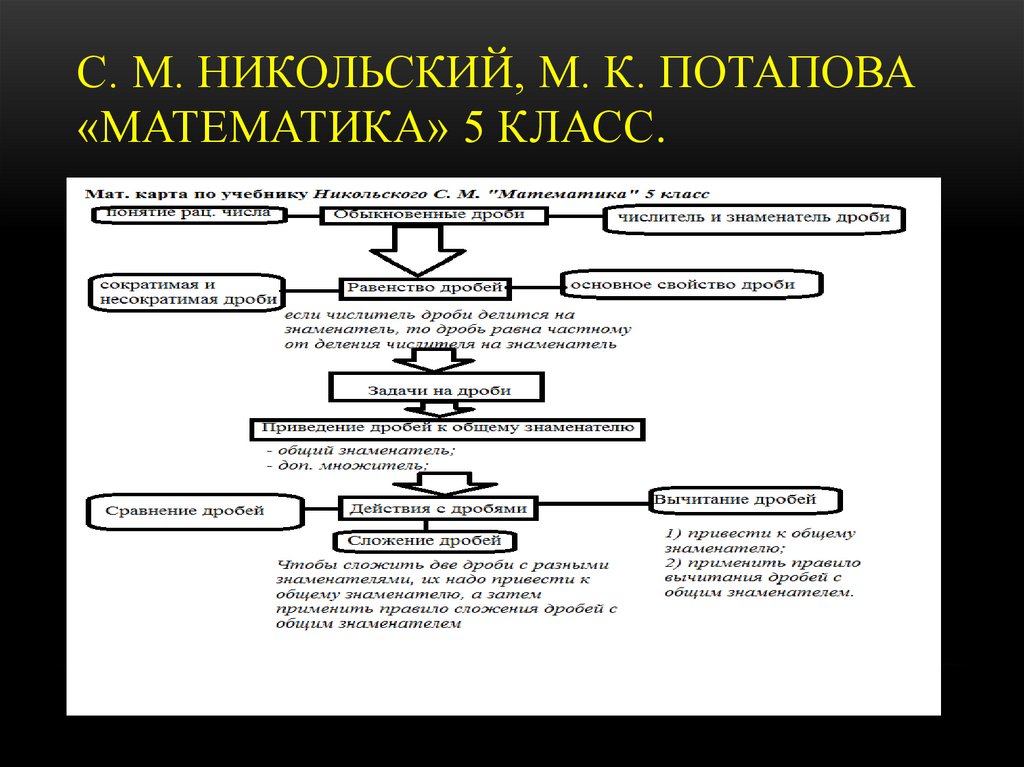
§3. ЛОГИКО-ДИДАКТИЧЕСКИЙ АНАЛИЗ ТЕМЫ
«СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С
РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ
1.Н. Я. Виленкин «Математика» 6
класс;
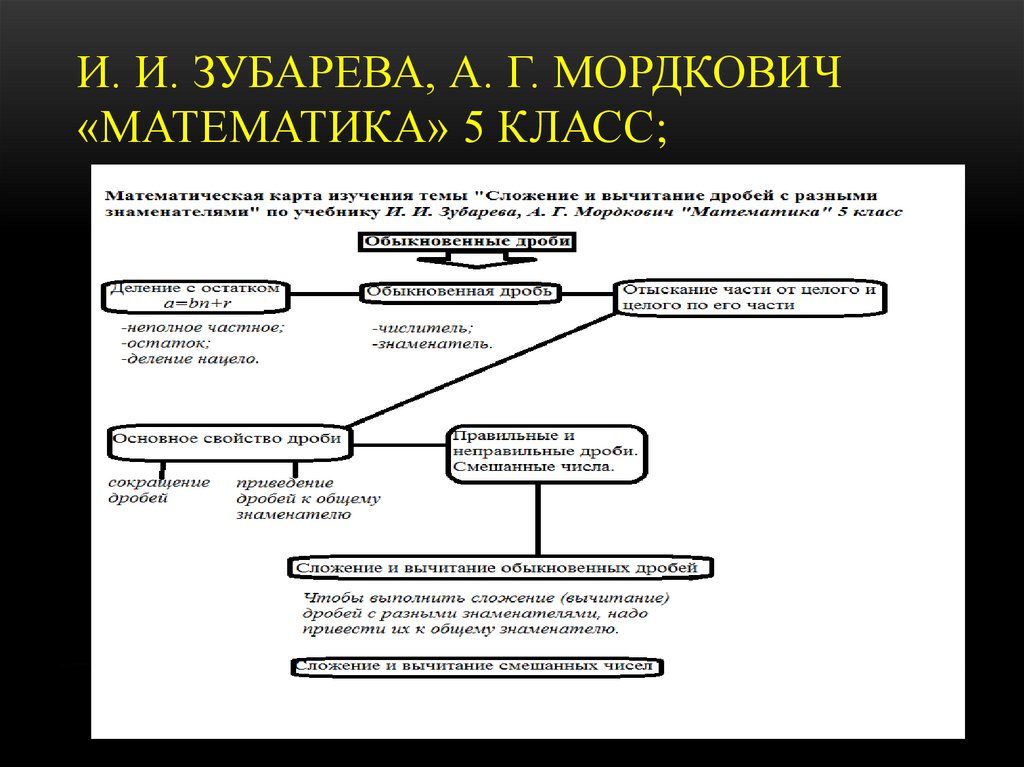
2.И. И. Зубарева, А. Г. Мордкович
«Математика» 5 класс;
3.С. М. Никольский, М. К. Потапова
«Математика» 5 класс.

12.

Н. Я. ВИЛЕНКИН «МАТЕМАТИКА» 6 КЛАСС;

13.

14.

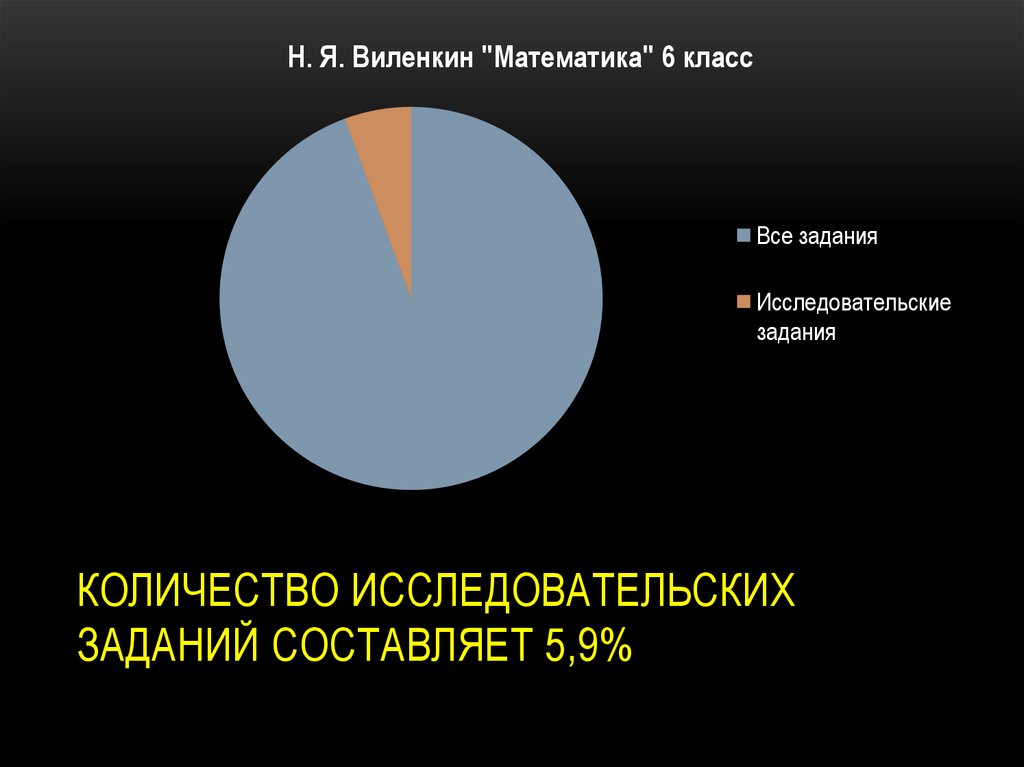
Н. Я. Виленкин "Математика" 6 класс
Все задания
Исследовательские
задания
КОЛИЧЕСТВО ИССЛЕДОВАТЕЛЬСКИХ
ЗАДАНИЙ СОСТАВЛЯЕТ 5,9%

15.

И. И. ЗУБАРЕВА, А. Г. МОРДКОВИЧ
«МАТЕМАТИКА» 5 КЛАСС;

16.

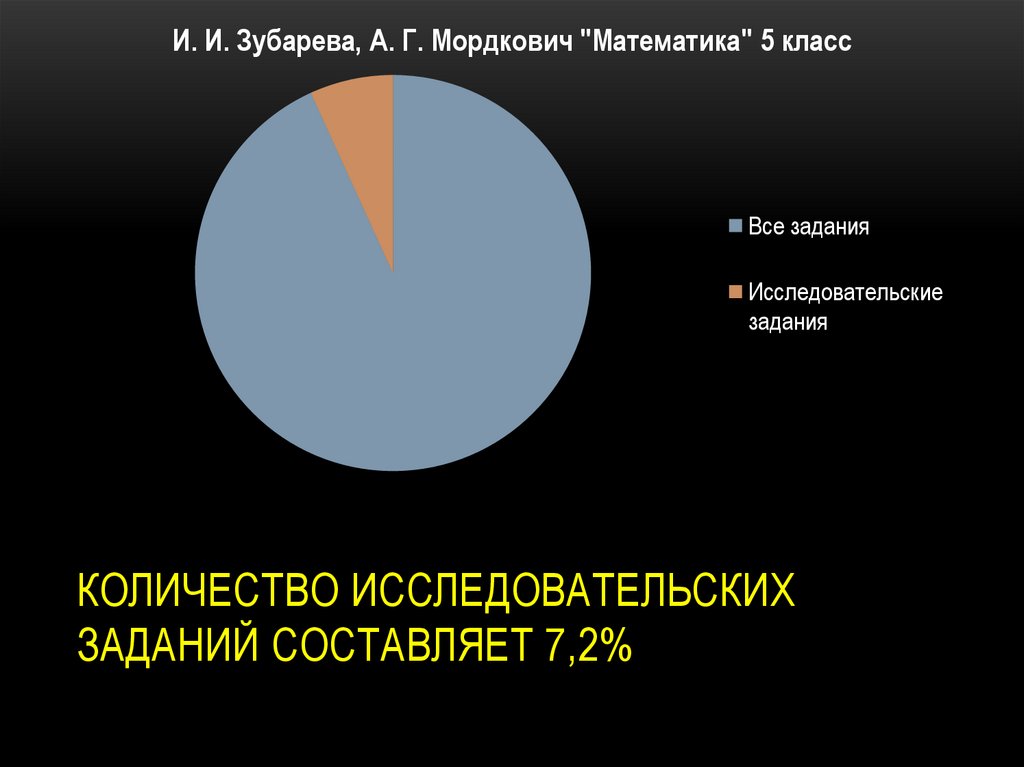
И. И. Зубарева, А. Г. Мордкович "Математика" 5 класс
Все задания
Исследовательские
задания
КОЛИЧЕСТВО ИССЛЕДОВАТЕЛЬСКИХ
ЗАДАНИЙ СОСТАВЛЯЕТ 7,2%

17.

С. М. НИКОЛЬСКИЙ, М. К. ПОТАПОВА
«МАТЕМАТИКА» 5 КЛАСС.

18.

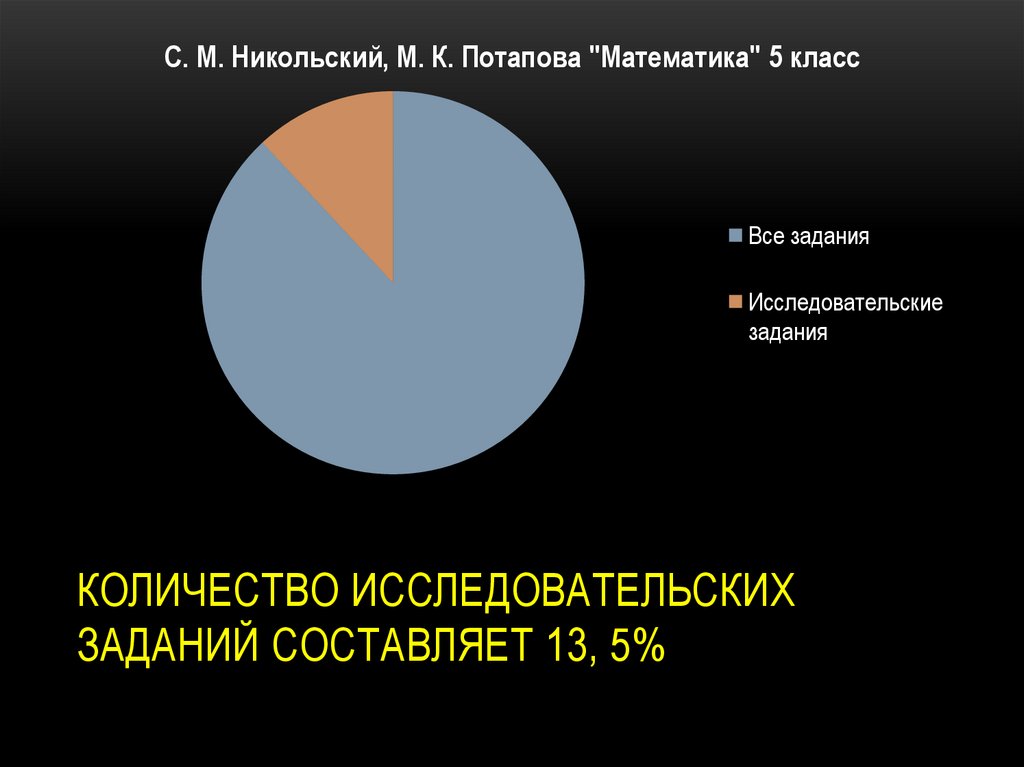
С. М. Никольский, М. К. Потапова "Математика" 5 класс
Все задания
Исследовательские
задания
КОЛИЧЕСТВО ИССЛЕДОВАТЕЛЬСКИХ
ЗАДАНИЙ СОСТАВЛЯЕТ 13, 5%

19.

ВЫВОДЫ ПО 1 ГЛАВЕ:
1.
2.
3.
4.
5.
6.
Исследовательская задача – это задача, процесс решения которой
предполагает самостоятельное осуществление учеником учебноисследовательской деятельности в полном её объеме или отдельных
её этапах.
Выделены признаки исследовательских заданий.
Выделены классификации исследовательских заданий.
Выделены этапы методики решения исследовательских заданий.
Обозначены дидактические приемы, использующиеся при решении
исследовательских заданий.
Выполнен логико-дидактический анализ темы, который показал, что
реализация исследовательской деятельности затруднена, из-за
недостаточного количества исследовательских заданий.

20.

ГЛАВА 2. ПРАКТИЧЕСКИЕ АСПЕКТЫ ПРИМЕНЕНИЯ
МЕТОДИКИ РЕШЕНИЯ ИССЛЕДОВАТЕЛЬСКИХ ЗАДАНИЙ ПО
ТЕМЕ «СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ
ЗНАМЕНАТЕЛЯМИ»
§1. Реализация исследовательской
деятельности через дидактические
приемы.
§2. Конспект нестандартного урока.
§3. Описание дидактических материалов
к урокам.

21.

§1. РЕАЛИЗАЦИЯ ИССЛЕДОВАТЕЛЬСКОЙ
ДЕЯТЕЛЬНОСТИ ЧЕРЕЗ
ДИДАКТИЧЕСКИЕ ПРИЕМЫ
В данном параграфе разработано 10 фрагментов урока,
содержащие перечисленные ранее дидактические
приемы.
Пример: учебник С. М. Никольского «Математика» 5
класс

22.

Для выполнения данного задания учащимся
раздаются карточки с заданием:
Задание 1: Найдите сумму двух правильных дробей.
Какая дробь получилась в результате суммы?
Обоснуйте ответ. Что помогло в обосновании ответа?
Сравните свое решение с предложенным ниже.

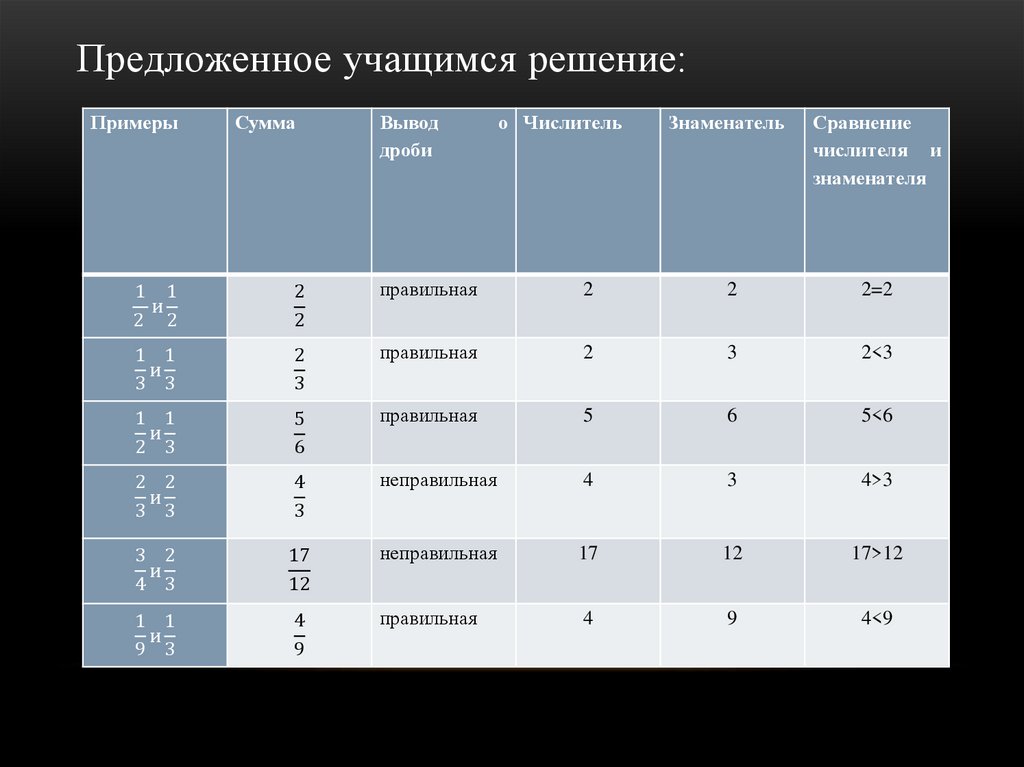
23.

Предложенное учащимся решение:
Примеры
Сумма
Вывод
дроби
о Числитель
Знаменатель
Сравнение
числителя и
знаменателя
1 1
и
2 2
2
2
правильная
2
2
2=2
1 1
и
3 3
2
3
правильная
2
3
2<3
1 1
и
2 3
5
6
правильная
5
6
5<6
2 2
и
3 3
4
3
неправильная
4
3
4>3
3 2
и
4 3
17
12
неправильная
17
12
17>12
1 1
и
9 3
4
9
правильная
4
9
4<9

24.

Затем учащиеся получают карточку с заданием №2.
Задание 2: Какова связь числителя и знаменателя правильной дроби;
неправильной дроби? Сформулируйте общий вывод по заданию.
Вывод, сформулированный учениками:
Дробь является правильной в том случае,
если у дроби, которая является суммой
двух обыкновенных дробей, числитель
меньше, либо равен знаменателю. Дробь
будет являться неправильной, если
числитель окажется больше знаменателя.

25.

§2. КОНСПЕКТ НЕСТАНДАРТНОГО
УРОКА
В данном параграфе разработан урок по теме:
«Старинные задачи на дроби».
Перед занятием, учащиеся должны подготовить доклад
на теме: «Об возникновении обыкновенных дробей».
Целью данного урока является повышение интереса
учащихся к изучению математике и углубление
понимания темы действия с дробями, а также
расширение умственного кругозора учащихся и
повышение их общей культуры.

26.

Спасибо за внимание!!!