Похожие презентации:
Значение логического выражения
1.
Высказывание – это форма мышления, в которой что-либоутверждается или отрицается о свойствах реальных предметов и
отношений между ними. Высказывание может быть либо
истинно, либо ложно
Высказывания обозначаются именами логических переменных,
которые могут принимать лишь два значения:
«Истина» (1) и «ложь» (0)
Например:
А= «Два умножить на два равно четырем»
В = «Два умножить на два равно пяти»
А=1, В=0
2.
Логическое умножение(конъюнкция):
&, *, · , ˄, И
Логическое сложение
(дизъюнкция): +, ˅, ИЛИ
Логическое
отрицание
(инверсия): НЕ, ̚ ,
Составное высказывание,
образованное в результате операции
логического умножения, истинно
тогда и только тогда, когда
истинны все входящие в него
простые высказывания
Составное высказывание,
образованное в результате
операции логического сложения,
истинно тогда, когда истинно
хоты бы одно из входящих в
него простых высказываний
Логическое отрицание
делает истинное
высказывание ложным
и, наоборот, ложное истинным
А
В
А*В
А
В
А+В
А
0
0
0
0
0
0
0
1
0
1
0
0
1
1
1
0
1
0
0
1
0
1
1
1
1
1
1
1
Приоритет действий: действия в скобках, отрицание, умножение, сложение
3.
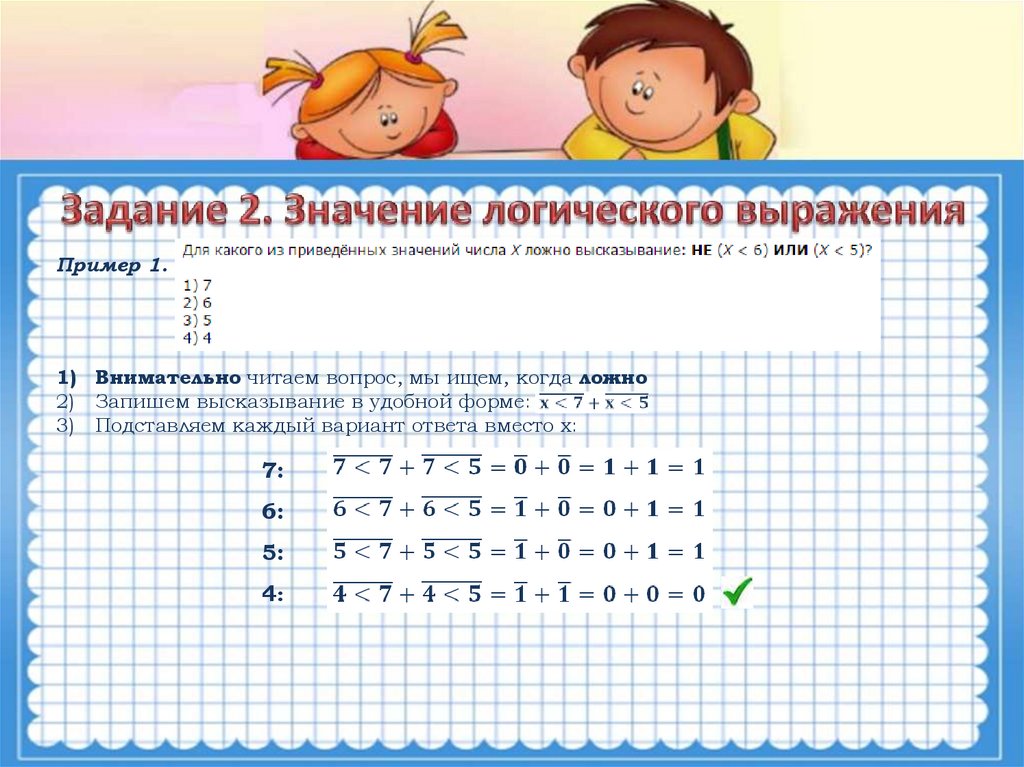
Пример 1.1) Внимательно читаем вопрос, мы ищем, когда ложно
2) Запишем высказывание в удобной форме:
3) Подставляем каждый вариант ответа вместо х:
7:
6:
5:
4:
4.
Пример 2.1) Внимательно читаем вопрос, мы ищем, когда истинно
2) Запишем высказывание в удобной форме:
3) Проверяем каждый вариант ответа
1234
6843
3561
4562
5.
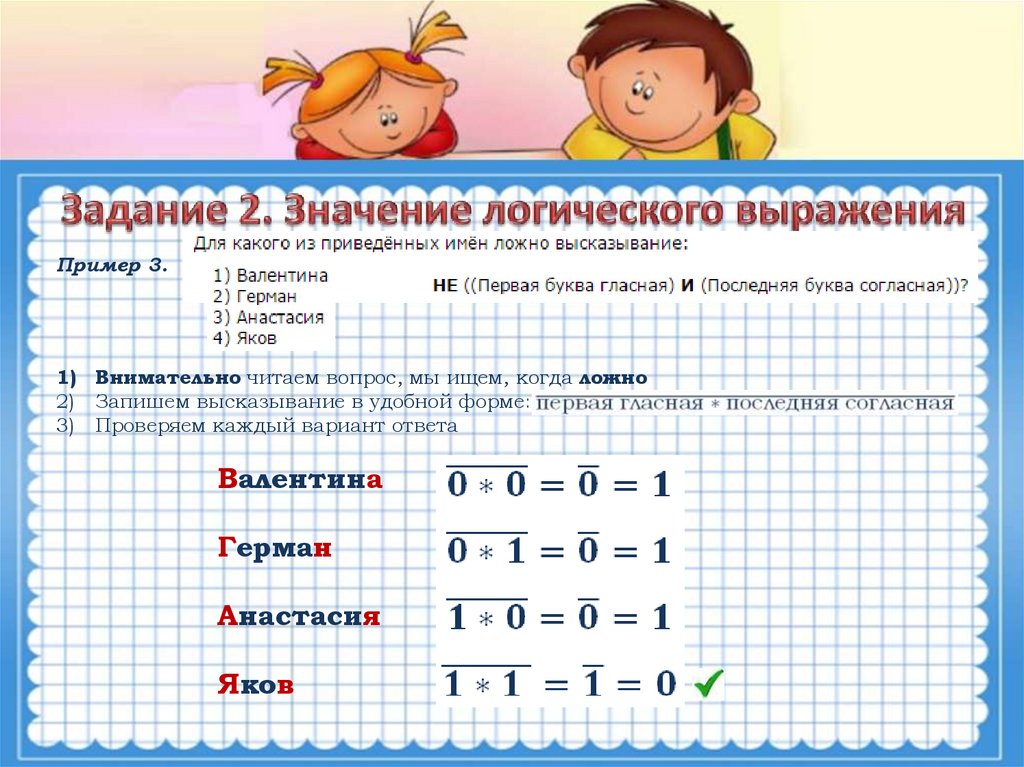
Пример 3.1) Внимательно читаем вопрос, мы ищем, когда ложно
2) Запишем высказывание в удобной форме:
3) Проверяем каждый вариант ответа
Валентина
Герман
Анастасия
Яков
6.
Пример 4. Сколько целых положительных чисел удовлетворяют следующемуусловию: (x ≤ 3) ИЛИ ((x ≤ 11) И (x > 8))?
1)6
2)11
3)3
4)7
Способ 1.
1) Внимательно читаем вопрос, мы ищем сколько, а не какое число, т.е. варианты
ответов – это количество чисел. Положительные числа – числа от 0 до ∞
2) Запишем высказывание в удобной форме: (x ≤ 3) + ((x ≤ 11) * (x > 8))
3) Не забываем, что сначала выполняем выражение в скобках, а затем сложение.
4) Скобку обозначим буквой А и запишем выражение (x ≤ 3) +А
(x ≤ 3) здесь для числе 1, 2, 3 будет истина, остальные – ложь. Мы знаем, что 1+0=1,
1+1=1, значит 1+А всегда истина. Эти числа нам подходят
5) Рассмотрим случаи, когда выражение (x ≤ 3) ложь, тогда в скобках ((x ≤ 11) * (x > 8))
обязательно должна быть истина. При умножении мы истину получаем, когда
истинны оба высказывания, значит мы ищем числа, удовлетворяющие условию
8<x ≤ 11. Это числа 9, 10, 11
Итак, нам подошли 6 чисел - 1, 2, 3, 9, 10, 11. Правильный ответ - 1
7.
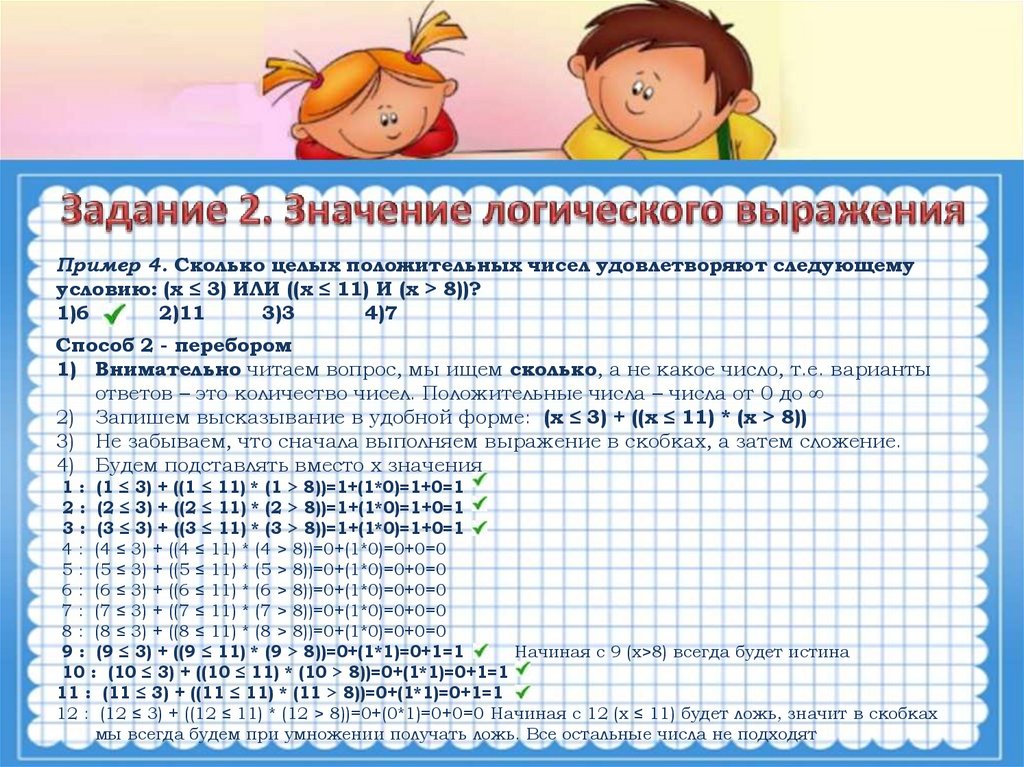
Пример 4. Сколько целых положительных чисел удовлетворяют следующемуусловию: (x ≤ 3) ИЛИ ((x ≤ 11) И (x > 8))?
1)6
2)11
3)3
4)7
Способ 2 - перебором
1) Внимательно читаем вопрос, мы ищем сколько, а не какое число, т.е. варианты
ответов – это количество чисел. Положительные числа – числа от 0 до ∞
2) Запишем высказывание в удобной форме: (x ≤ 3) + ((x ≤ 11) * (x > 8))
3) Не забываем, что сначала выполняем выражение в скобках, а затем сложение.
4) Будем подставлять вместо х значения
1 : (1 ≤ 3) + ((1 ≤ 11) * (1 > 8))=1+(1*0)=1+0=1
2 : (2 ≤ 3) + ((2 ≤ 11) * (2 > 8))=1+(1*0)=1+0=1
3 : (3 ≤ 3) + ((3 ≤ 11) * (3 > 8))=1+(1*0)=1+0=1
4 : (4 ≤ 3) + ((4 ≤ 11) * (4 > 8))=0+(1*0)=0+0=0
5 : (5 ≤ 3) + ((5 ≤ 11) * (5 > 8))=0+(1*0)=0+0=0
6 : (6 ≤ 3) + ((6 ≤ 11) * (6 > 8))=0+(1*0)=0+0=0
7 : (7 ≤ 3) + ((7 ≤ 11) * (7 > 8))=0+(1*0)=0+0=0
8 : (8 ≤ 3) + ((8 ≤ 11) * (8 > 8))=0+(1*0)=0+0=0
9 : (9 ≤ 3) + ((9 ≤ 11) * (9 > 8))=0+(1*1)=0+1=1
Начиная с 9 (х>8) всегда будет истина
10 : (10 ≤ 3) + ((10 ≤ 11) * (10 > 8))=0+(1*1)=0+1=1
11 : (11 ≤ 3) + ((11 ≤ 11) * (11 > 8))=0+(1*1)=0+1=1
12 : (12 ≤ 3) + ((12 ≤ 11) * (12 > 8))=0+(0*1)=0+0=0 Начиная с 12 (х ≤ 11) будет ложь, значит в скобках
мы всегда будем при умножении получать ложь. Все остальные числа не подходят




 Математика
Математика








