Похожие презентации:
Потери напора на местных гидравлических сопротивлениях
1. Местные гидравлические сопротивления
Лекция №12Местные гидравлические
сопротивления
Рассматриваемые вопросы:
1)Общая характеристика местных потерь
напора;
2)Резкое расширение. Формула Борда;
3)Отдельные случаи частных потерь.
2.
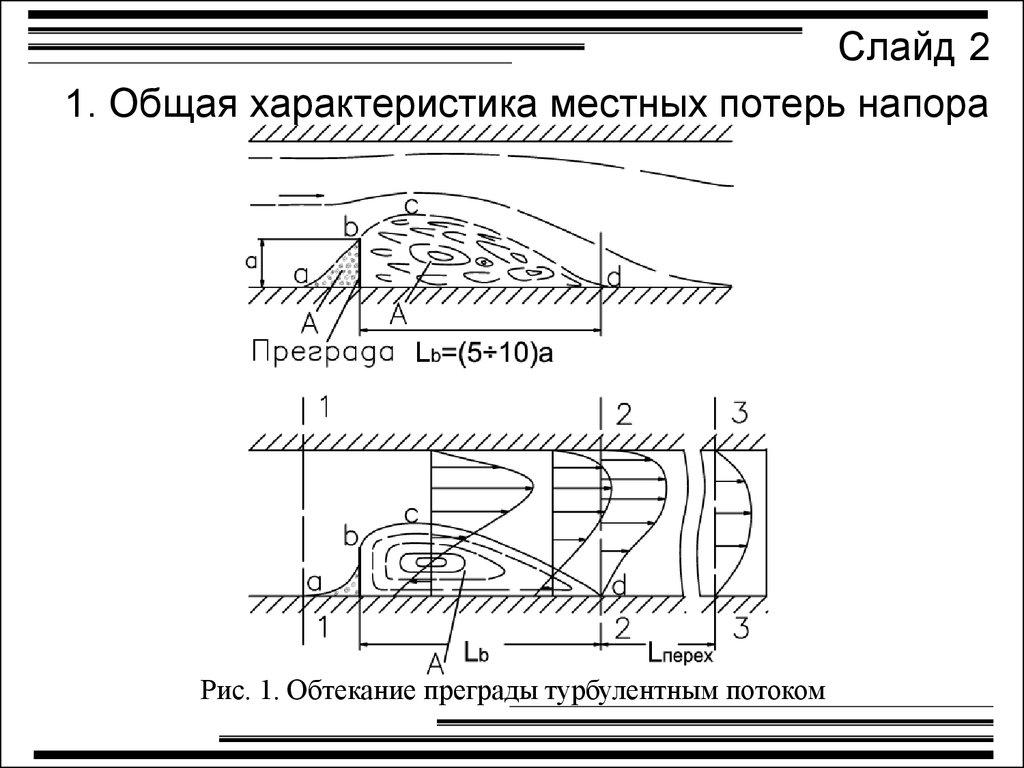
Слайд 21. Общая характеристика местных потерь напора
Рис. 1. Обтекание преграды турбулентным потоком
3.
Слайд 2.11. Общая характеристика местных потерь напора
Рис. Изменение эпюры скоростей за местным сопротивлением
4.
Слайд 32. Резкое расширение. Формула Борда
а)
б)
Рис. 2. К выводу формулы
Борда. Резкое расширение
трубопровода
5.
Слайд 42. Резкое расширение. Формула Борда
а)
Рис. 2. К выводу формулы Борда. Резкое расширение трубопровода
(h )
j p.p
6.
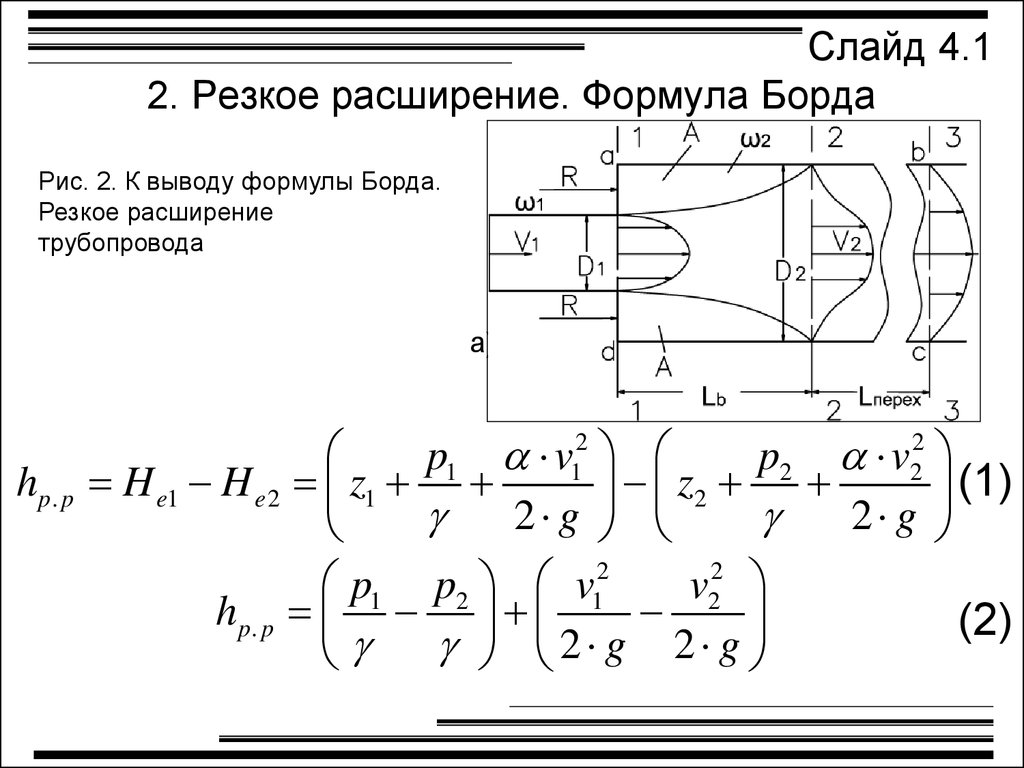
Слайд 4.12. Резкое расширение. Формула Борда
Рис. 2. К выводу формулы Борда.
Резкое расширение
трубопровода
а)
hp . p
p1 v12
p2 v22
(1)
H e1 H e 2 z1
z2
2 g
2 g
2
2
p1 p2
v1
v2
hp. p
(2)
2 g 2 g
7.
Слайд 52. Резкое расширение. Формула Борда
0 Q v2 v1 T0 S GS PS RS
0 1
(T )S = 0
GS 0
RS R
PS P1 P2
(3)
(1-е допущение)
8.
Слайд 62. Резкое расширение. Формула Борда
PS RS
Я
PS RS P1 P2 R P1 R P2
P1 R p1 2
(5)
P2 p2 2
PS RS p1 2 p2 2
(4)
(6)
(7)
Примем, что давление по всему сечению 1–1 (по площади ad,
охватывающей транзитную струю и водоворотную область)
распределяется также по гидростатическому закону
(2-е допущение)
9.
Слайд 72. Резкое расширение. Формула Борда
Учитывая (7), уравнение (3) переписываем виде
Q v2 v1 p1 2 p2 2
откуда, имея в
виду, что
g
v2
Q v2 v1 v2 v1
v2
2 g
g
p1
p2
(8)
Q
2
(11)
10.
Слайд 82. Резкое расширение. Формула Борда
Подставляя (11) в (2), имеем
hp. p
2 v2 v1
v12
v22
v2
2 g 2 g
2 g
v12 v22 2 v22 2 v1 v2
2 g
или
окончательно
hp. p
(12)
v1 v2
2 g
2
(13)
11.
Слайд 92. Резкое расширение. Формула Борда
Приведем выражение (13) к другому виду. Вынесем за
скобки v1 , тогда подучим
2
hp . p
2
v2 v
1 v12
1
1
v1 2 g 2 2 g
2
1
(14)
2
Обозначая
имеем
1
1 P. P
2
hp. p
2
1
v
p. p
2 g
(15)
(16)
12.
Слайд 103. Отдельные случаи частных потерь
а) Выход из трубопровода
hвых
потере «на выход»
2 1
вых 1,0
Рис. 3. Потери напора
на выход
hвых
2
1
v
2 g
(19)
(20)
13.
Слайд 113. Отдельные случаи частных потерь
б) Постепенное расширение
Рис. Диффузор
14.
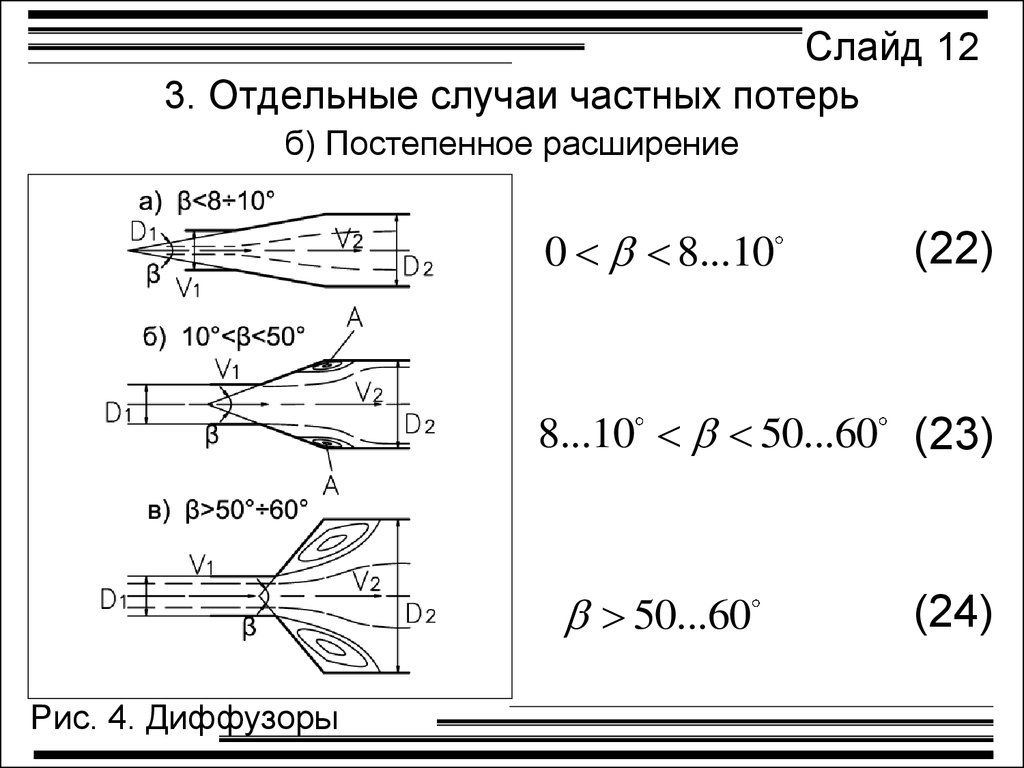
Слайд 123. Отдельные случаи частных потерь
б) Постепенное расширение
0 8...10
(22)
8...10 50...60 (23)
50...60
Рис. 4. Диффузоры
(24)
15.
Слайд 133. Отдельные случаи частных потерь
б) Постепенное расширение
hдифф у hp. p
(25)
коэффициент полноты
удара, определяемый
по графику рис. 5
Рис. 5. Коэффициент
полноты удара
16.
Слайд 143. Отдельные случаи частных потерь
б) Постепенное расширение
В настоящее время используются и
другие расчетные подходы
2
дифф
1
2,6 sin 1 45
2 2
2
дифф
1
1 45
2
(26)
17.
Слайд 153. Отдельные случаи частных потерь
в) Сужение и вход в трубопровод
Рис. 7. Сужение
трубопровода
18.
Слайд 163. Отдельные случаи частных потерь
в) Сужение и вход в трубопровод
Рис. 8. Наиболее резкое сужение трубопровода
19.
Слайд 173. Отдельные случаи частных потерь
в) Сужение и вход в трубопровод
hн. p.с
vС v2
2 g
2
2
2
2
2
v22
vC
v
1
1
v2
2 g C
2 g
2
2
1 v
1
2 g
2
2
(29)
или
hн. p.с
где коэффициент
сопротивления
наиболее резкого
сужения потока равен
н . p .с
2
2
v
н . р .с
2 g
1
1
(30)
2
(31)
20.
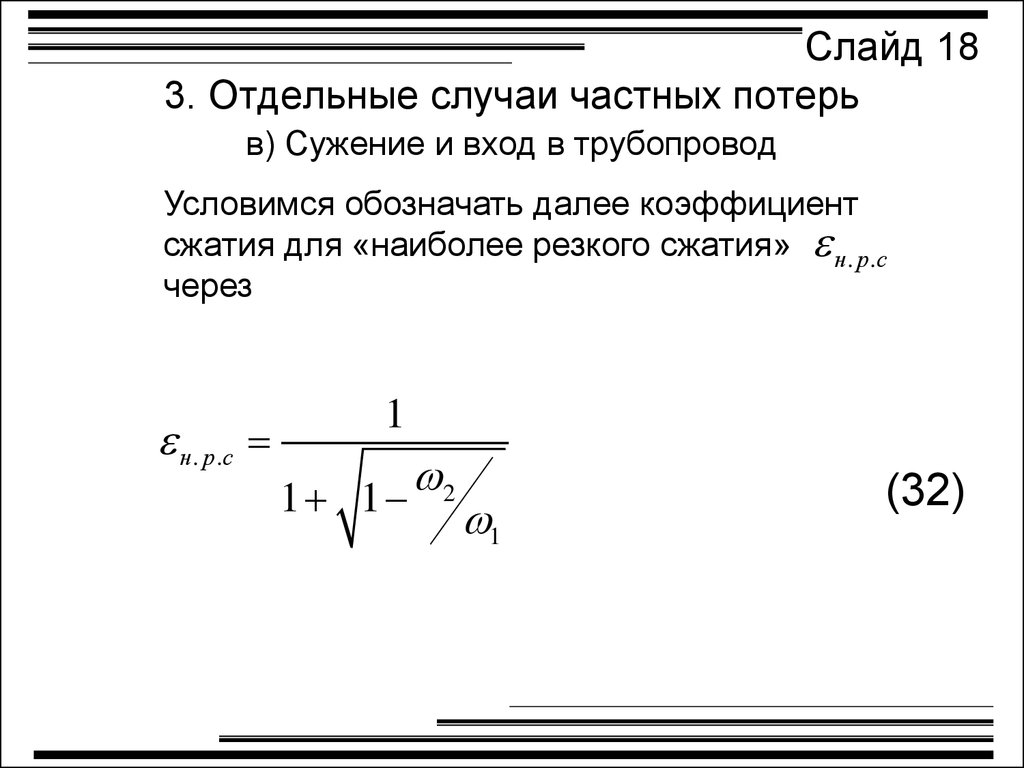
Слайд 183. Отдельные случаи частных потерь
в) Сужение и вход в трубопровод
Условимся обозначать далее коэффициент
сжатия для «наиболее резкого сжатия» н. р.с
через
н . р .с
1
1 1
2
1
(32)
21.
Слайд 193. Отдельные случаи частных потерь
в) Сужение и вход в трубопровод
2
2
v
hc c
2 g
c н . р .с
(33)
2
1
1
22.
Слайд 203. Отдельные случаи частных потерь
в) Сужение и вход в трубопровод
0,5
находится в зависимости от угла
и отношения a/D2
находится в зависимости от угла
и отношения r/D2
Рис. 7. Сужение
трубопровода
23.
Слайд 213. Отдельные случаи частных потерь
в) Сужение и вход в трубопровод
c н . р .с
1
вх 0,5
2
1
1
вх
для случая «резкое
сужение»
24.
Слайд 223. Отдельные случаи частных потерь
в) Сужение и вход в трубопровод
v2
hj j
2 g
(38)
формула Вейсбаха
Рис. 9. Протекание жидкости при наличии
задвижки (а) и при наличии поворота трубы (б)




















 Промышленность
Промышленность








