Графики тригонометрических функций

1.

Графики
тригонометрических
функций

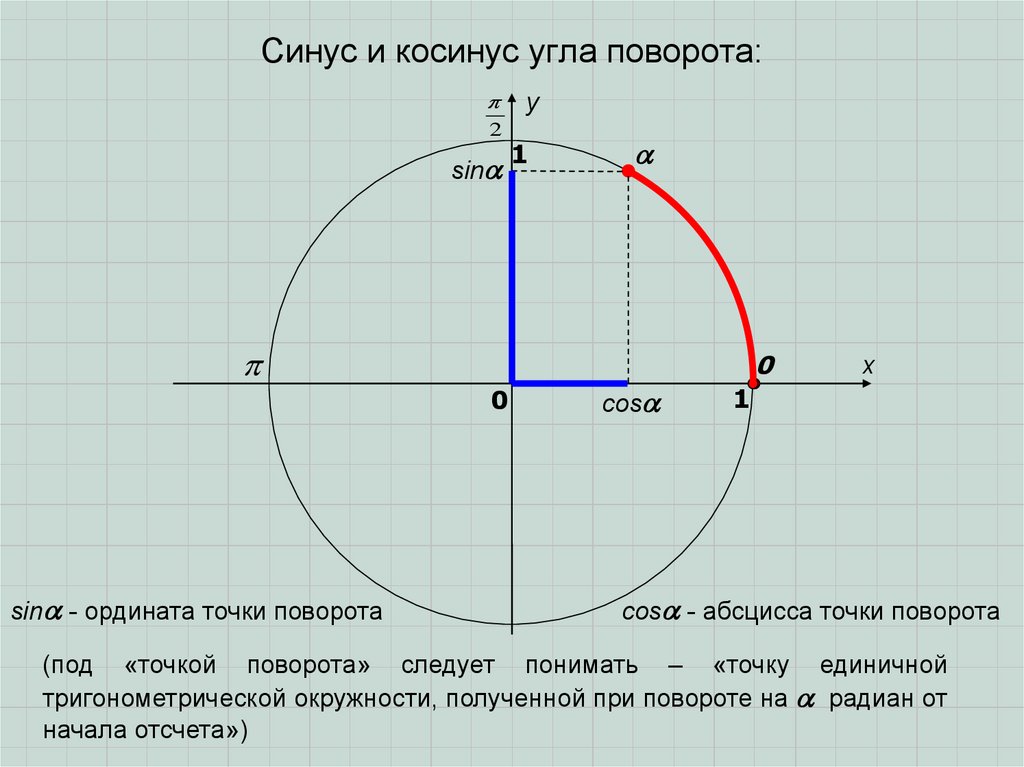
2. Синус и косинус угла поворота:

2
sin
1
0
0
sin - ордината точки поворота
y
cos
x
1
cos - абсцисса точки поворота
(под «точкой поворота» следует понимать – «точку единичной
тригонометрической окружности, полученной при повороте на радиан от
начала отсчета»)

3.

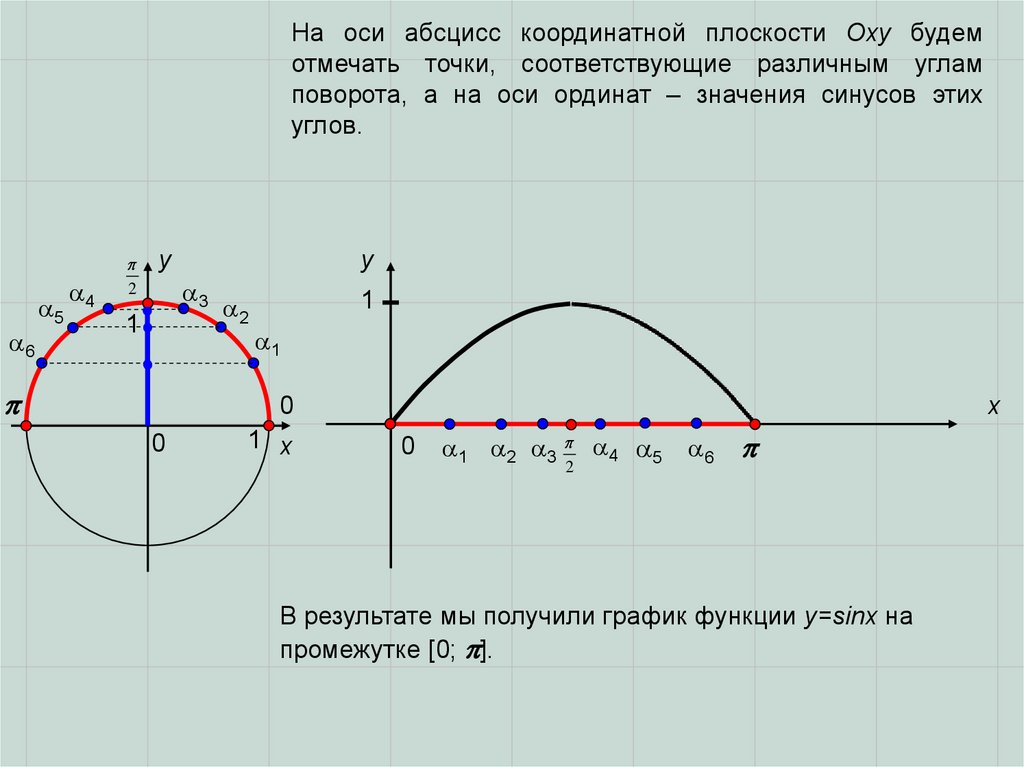
На оси абсцисс координатной плоскости Оху будем
отмечать точки, соответствующие различным углам
поворота, а на оси ординат – значения синусов этих
углов.
6
5
4
2
y
y
3
1
2
1
1
0
0
1 x
x
0
1 2 3 4 5
2
6
В результате мы получили график функции y=sinx на
промежутке [0; ].

4.

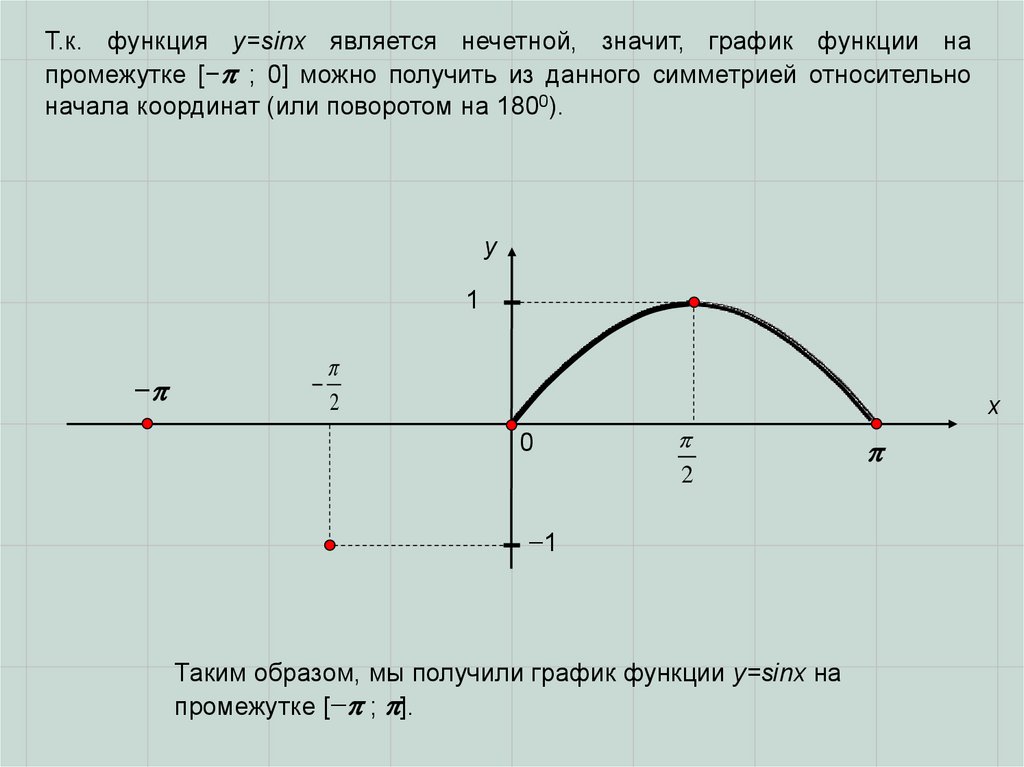
Т.к. функция y=sinx является нечетной, значит, график функции на
промежутке [− ; 0] можно получить из данного симметрией относительно
начала координат (или поворотом на 1800).
y
1
−
2
x
0
2
−1
Таким образом, мы получили график функции y=sinx на
промежутке [− ; ].

5.

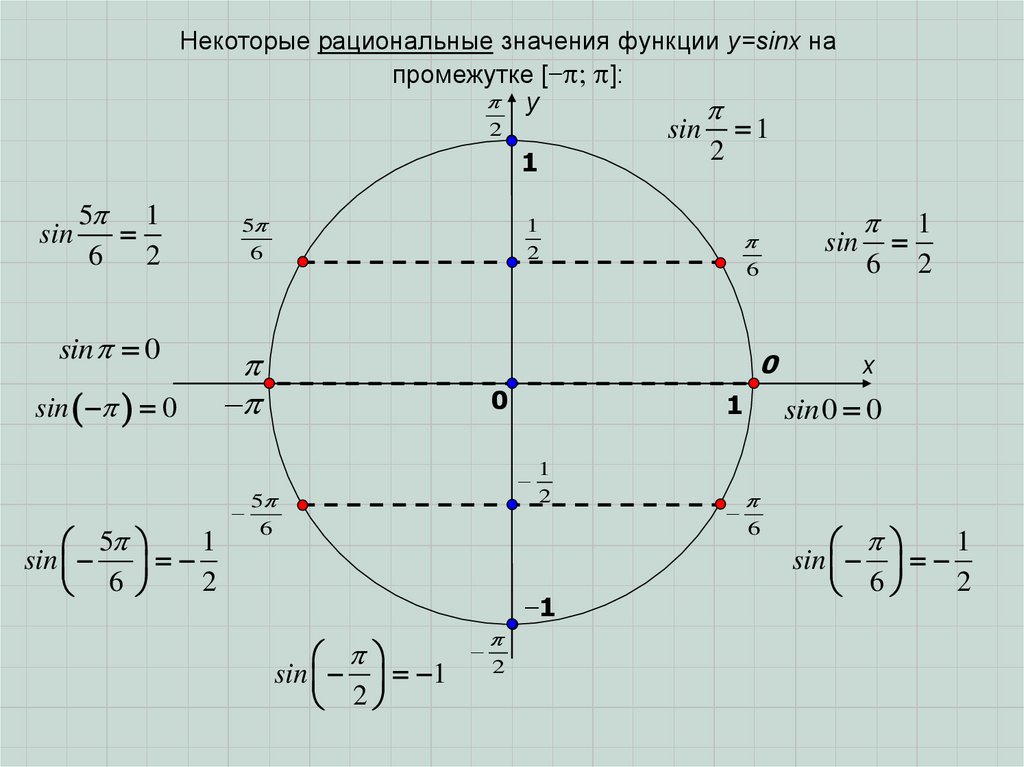
Некоторые рациональные значения функции у=sinx на
промежутке [− ; ]:
y
sin
2
1
sin
5 1
6
2
sin 0
sin 0
1
5
sin
2
6
5
6
1
2
2
1
sin
6
0
0
1
5
6
1
2
−1
sin 1
2
2
6
1
2
x
sin 0 0
6
1
sin
2
6

6.

На практике, для построения графика функции у=sinx на промежутке [0; ],
сначала отмечают точки с координатами (0; 0), ( /6; 0,5), ( /2; 1), ( 5 /6; 0,5)
и ( ; 0). Они образуют своеобразную «арку», которая периодически (с
периодом ) отображается симметрично оси Ох.
y
1
5
6
2
3
2
2
3
2
1
2
6
0
1
2
6
2
5
6
2
−1
После этого используют свойство периодичности функции у=sinx. Так как
наименьший положительный период функции y=sinx равен 2 , то
изображенный участок графика можно параллельно переносить влево и
вправо вдоль оси Ох на 2 n (n ) единичных отрезков.
График функции y=sinx называется синусоидой.
x

7.

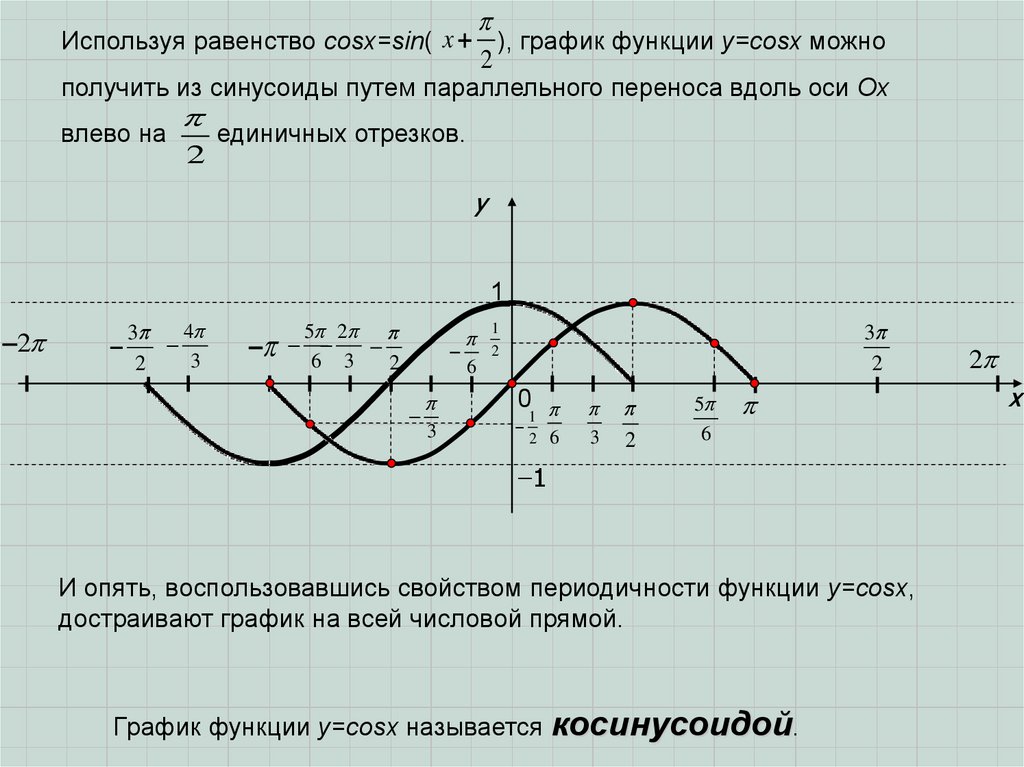
x
Используя равенство cosx=sin(
), график функции у=cosx можно
2
получить из синусоиды путем параллельного переноса вдоль оси Ох
влево на
2
единичных отрезков.
y
1
2
4
3
3
2
5 2
6 3
2
3
3
2
1
2
6
0
1
2
6
3
2
5
6
−1
И опять, воспользовавшись свойством периодичности функции y=cosx,
достраивают график на всей числовой прямой.
График функции y=cosx называется косинусоидой.
2
x

8.

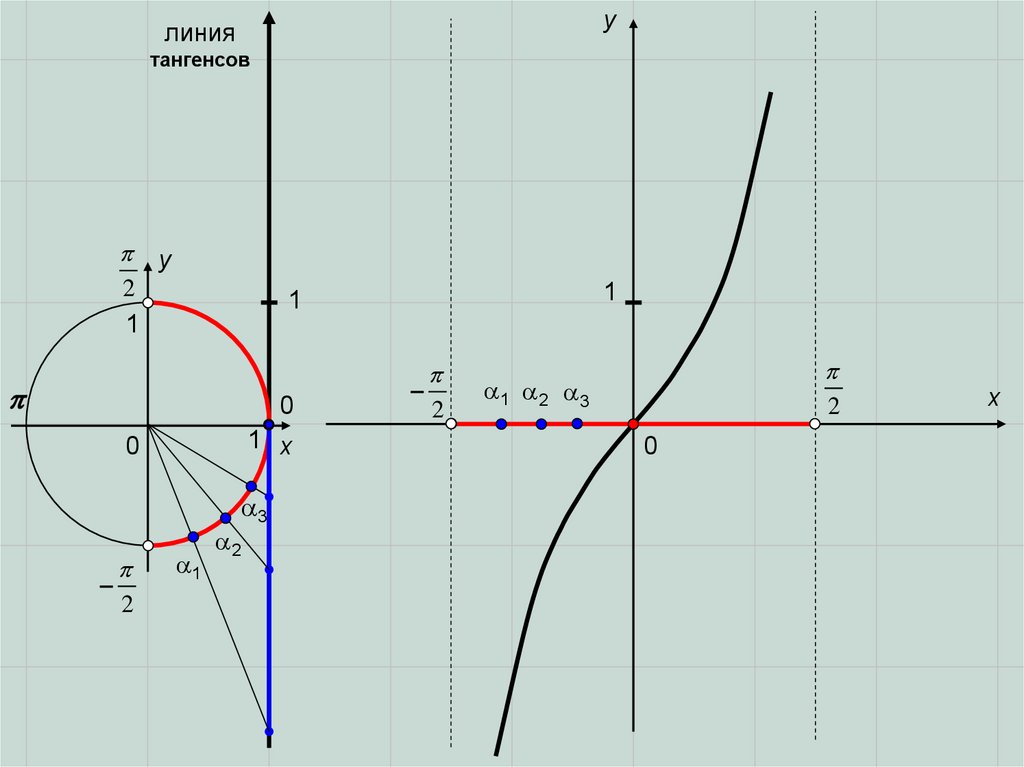
y
линия
тангенсов
y
2
1
0
1 x
0
2
1
1
1
2
3
2
2
1 2 3
0
x

9.

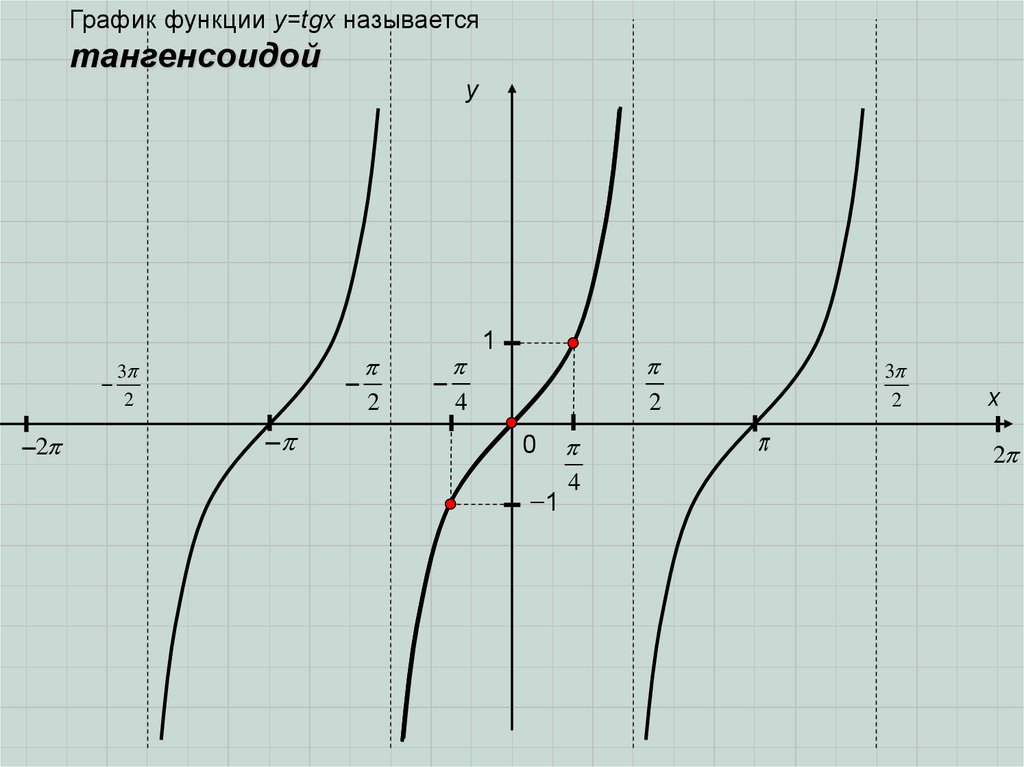
График функции y=tgx называется
тангенсоидой
y
2
3
2
2
1
2
4
0
−1
4
3
2
x
2

10.

График функции y=ctgx называется
котангенсоидой
y
1
2
3
2
0
2
4
2
3
4
−1
Масштаб :3
3
2
x
2

11.

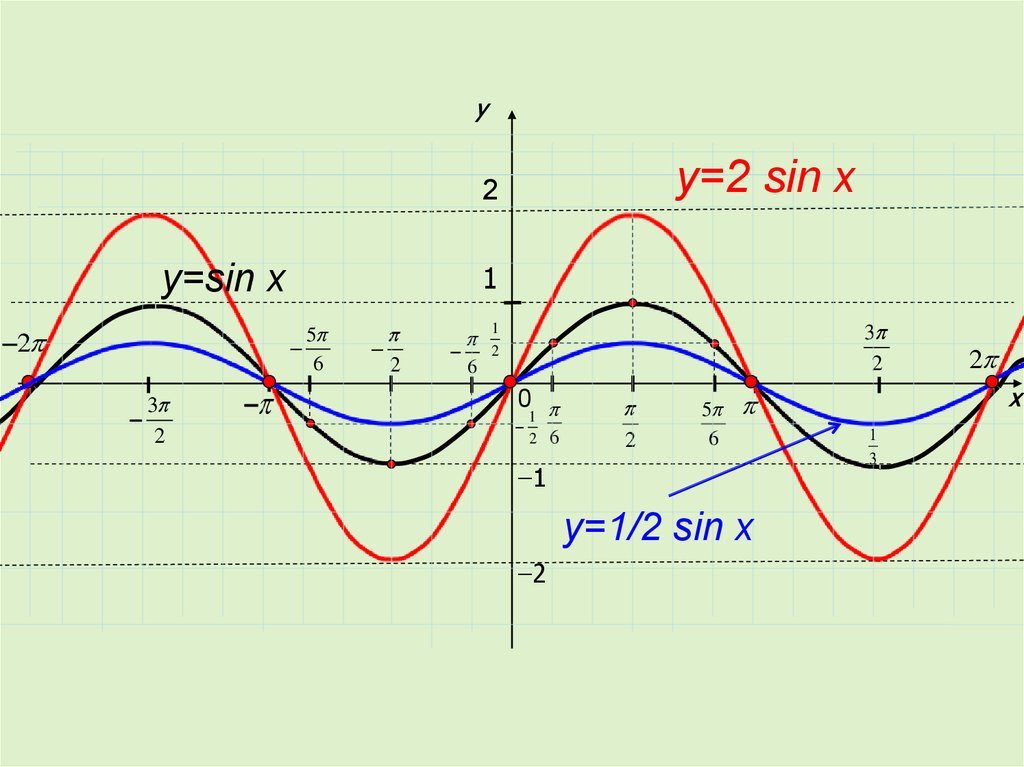
y
y=2 sin x
2
1
y=sin x
5
6
2
3
2
2
3
2
1
2
6
0
1
2
6
2
5
6
y=1/2 sin x
−2
x
−1
2
1
3

12.

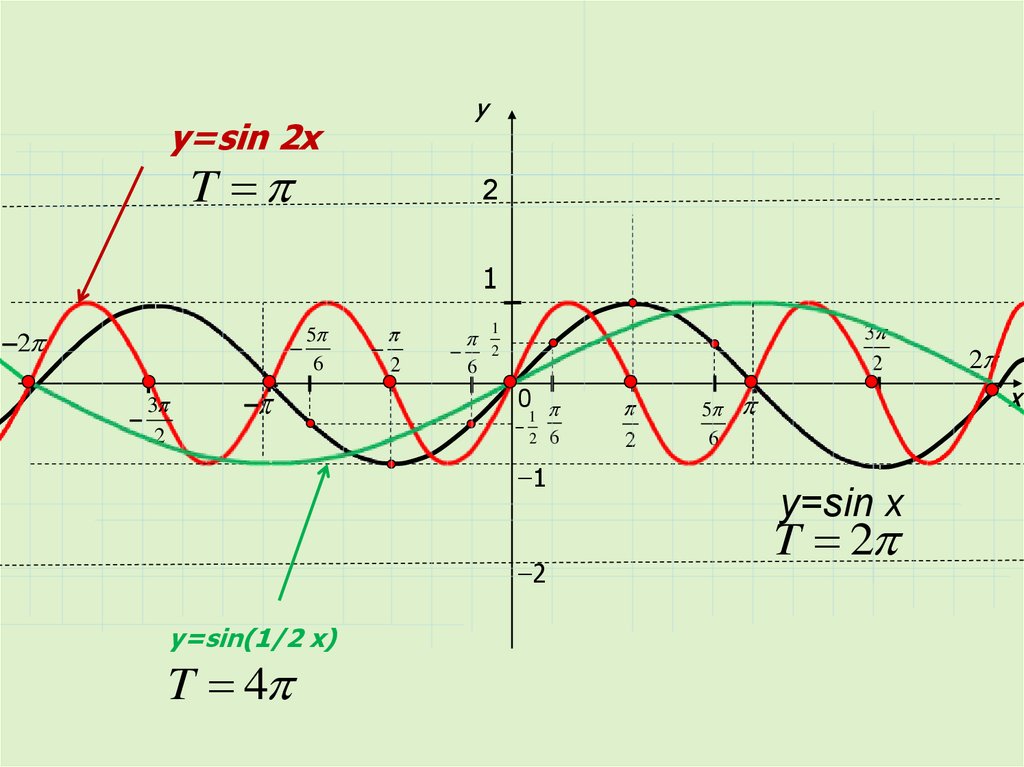
y
y=sin 2x
T
2
1
5
6
2
3
2
2
3
2
1
2
6
0
1
2
−1
−2
y=sin(1/2 x)
T 4
6
2
5
6
2
x
y=sin x
T 2

13.

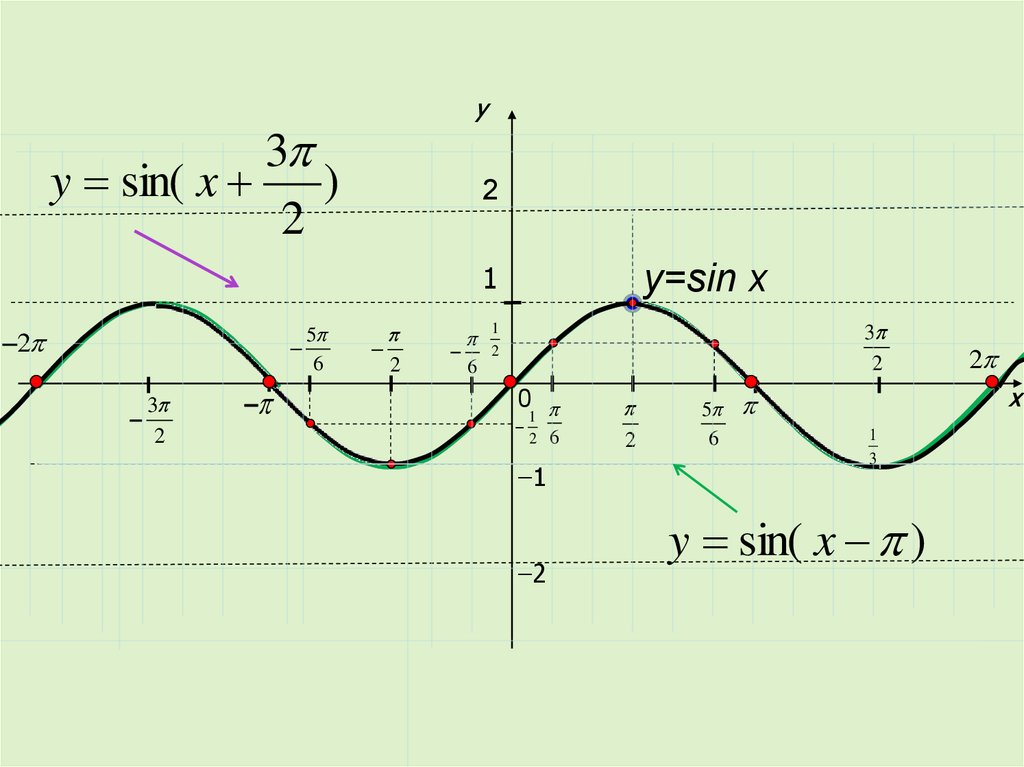
y
3
y sin( x )
2
2
1
5
6
2
3
2
2
y=sin x
3
2
1
2
6
0
1
2
−1
−2
6
2
5
6
2
x
1
3
y sin( x )