Построение графиков тригонометрических функций

1.

2.

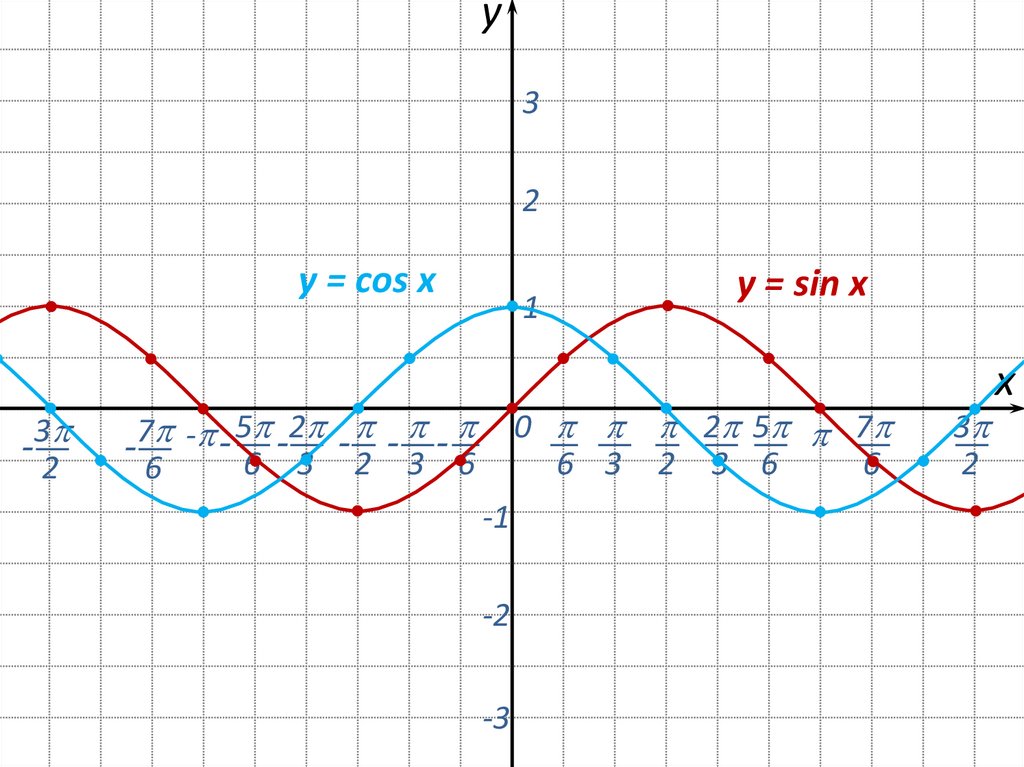
ОПРЕДЕЛЕНИЕ
Числовые функции, заданные формулами
y = sin x и y = cos x, называют
соответственно синусом и косинусом.

3.

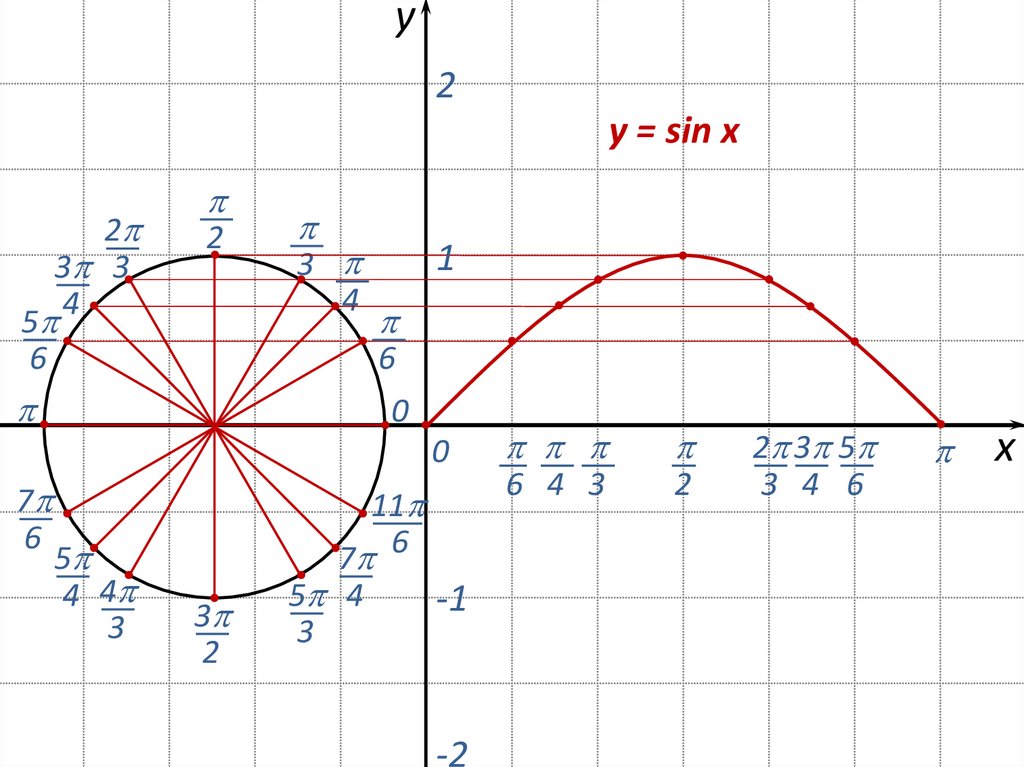
y
2
y = sin x
2
3 3
4
2
5
6
3
4
1
6
0
0
7
6
5
4 4
3
11
7 6
3
2
5 4
3
-1
-2
6 4 3
2
2 3 5
3 4 6
х

4.

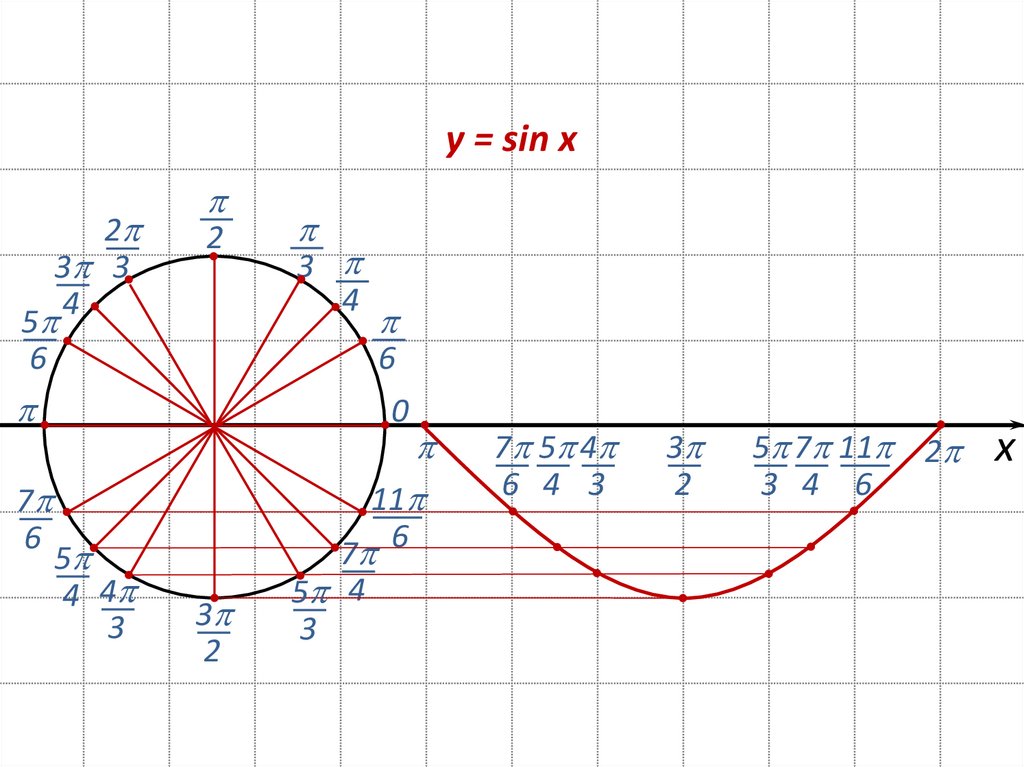
y = sin x
2
3 3
4
2
5
6
3
4
6
7
6
0
5
4 4
3
11
6
7
3
2
5 4
3
7 5 4
6 4 3
3
2
5 7 11 2
3 4 6
х

5.

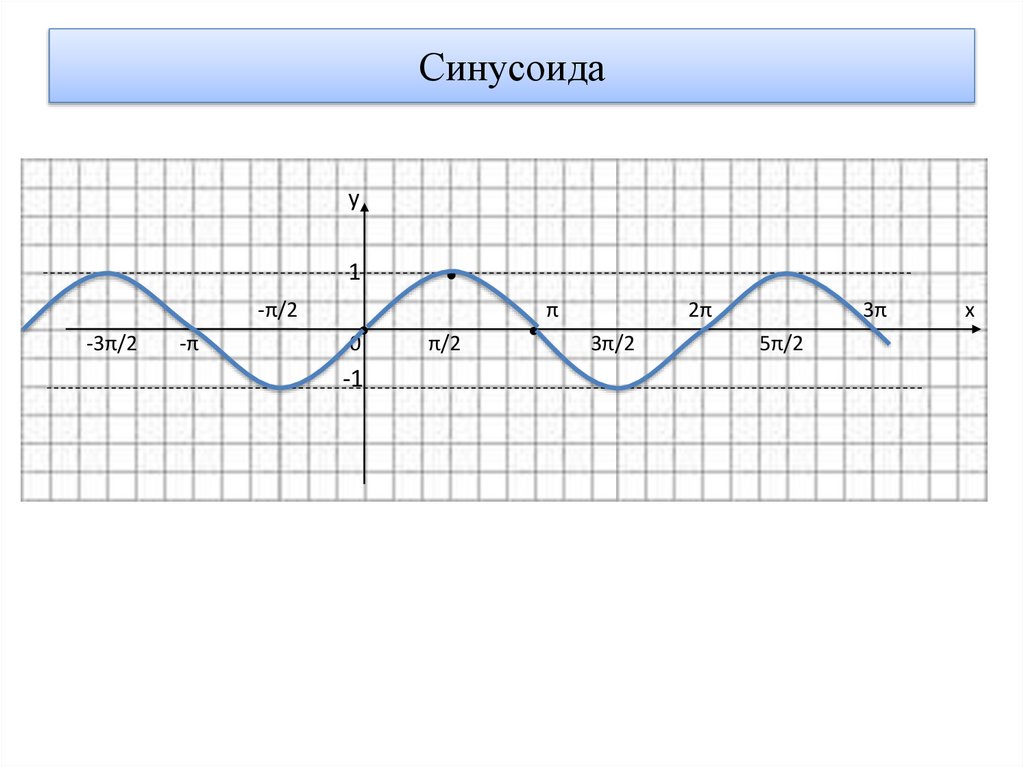
Синусоида
у
1
-π/2
-3π/2
-π
π
0
-1
π/2
2π
3π/2
3π
5π/2
х

6.

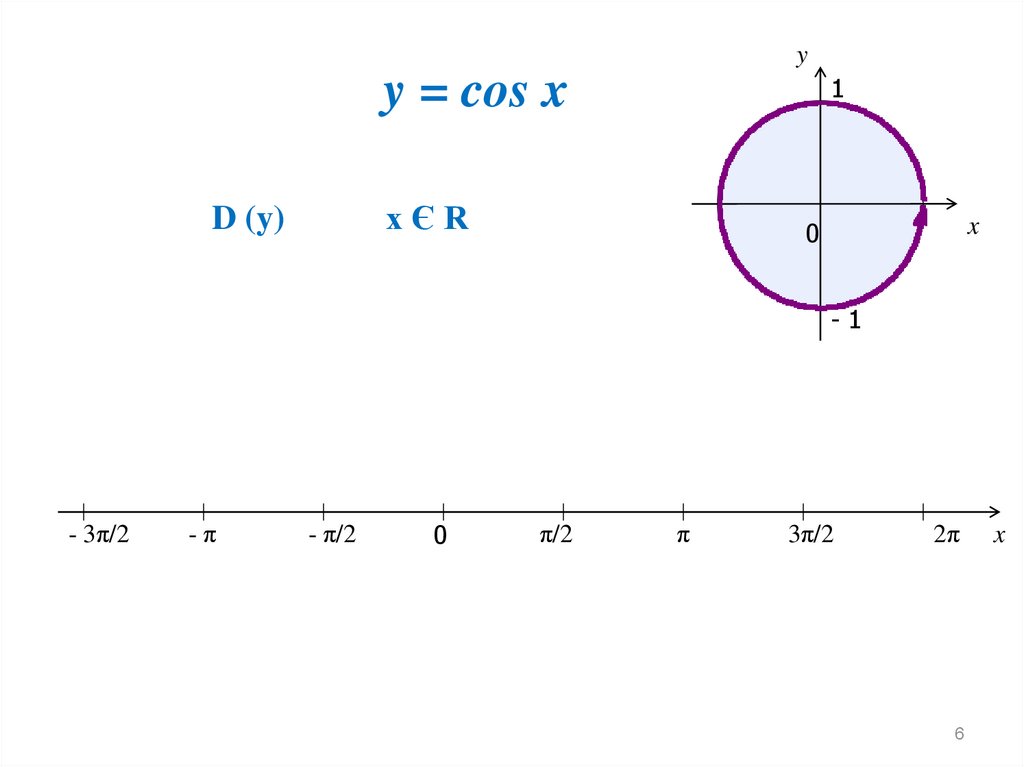
y
y = cos x
1
xЄR
D (y)
x
0
-1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
6
x

7.

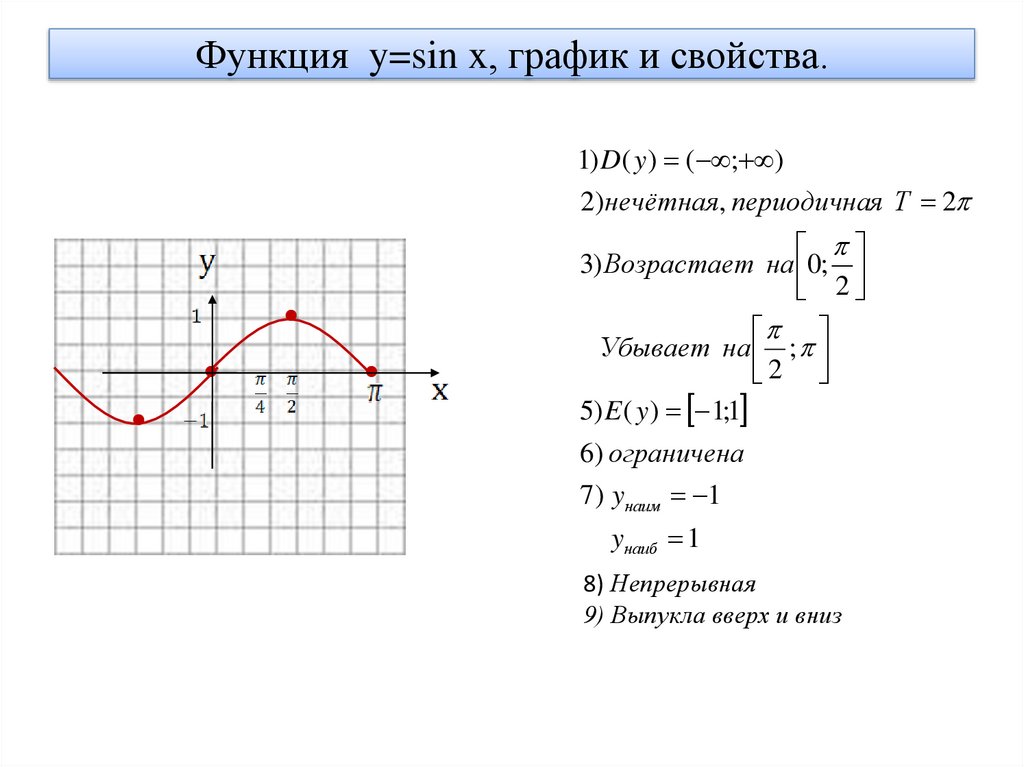
Функция y=sin x, график и свойства.
1) D( y ) ( ; )
2)нечётная, периодичная Т 2
3) Возрастает на 0;
2
Убывает на ;
2
5) E ( y ) 1;1
6) ограничена
7) yнаим 1
yнаиб 1
8) Непрерывная
9) Выпукла вверх и вниз

8.

y
y = cos x
E (y)
1
0
[ -1; 1]
y
x
-1
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
8
x

9.

y = сos x
y
1
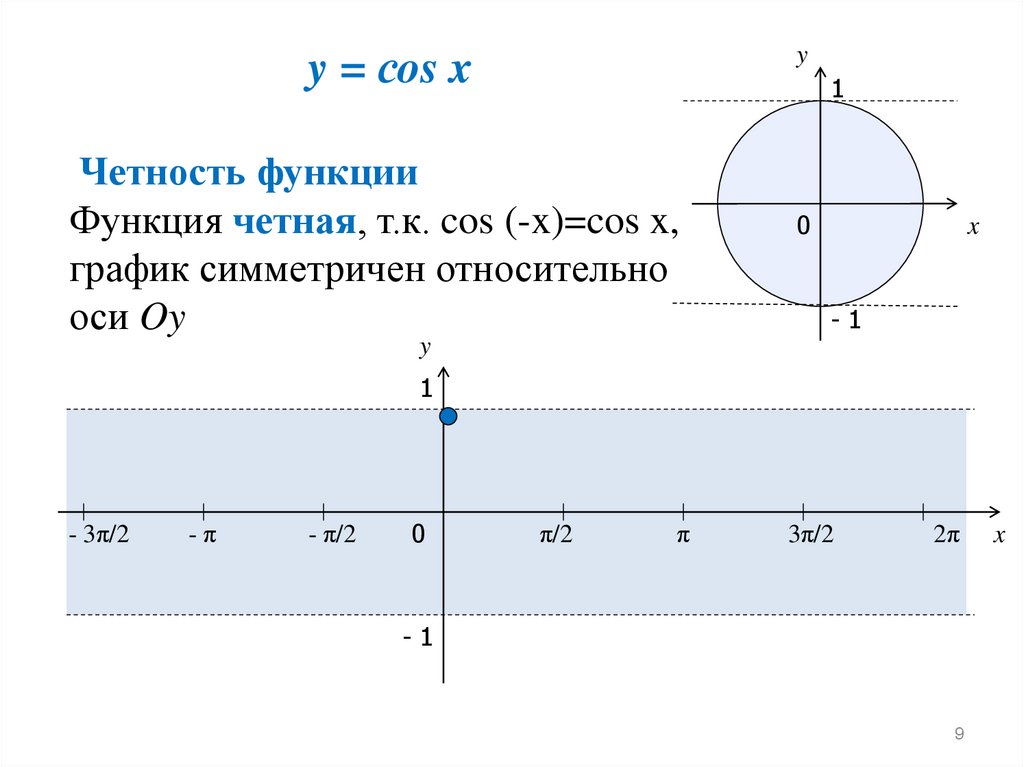
Четность функции
Функция четная, т.к. cos (-x)=cos x,
график симметричен относительно
оси Oy
0
x
-1
y
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
9
x

10.

y
y = cos x
1
Периодичность функции
0
Период функции Т=2π,
cos (x+2π)=cos x
x
-1
y
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
10
x

11.

y
y = cos x
1
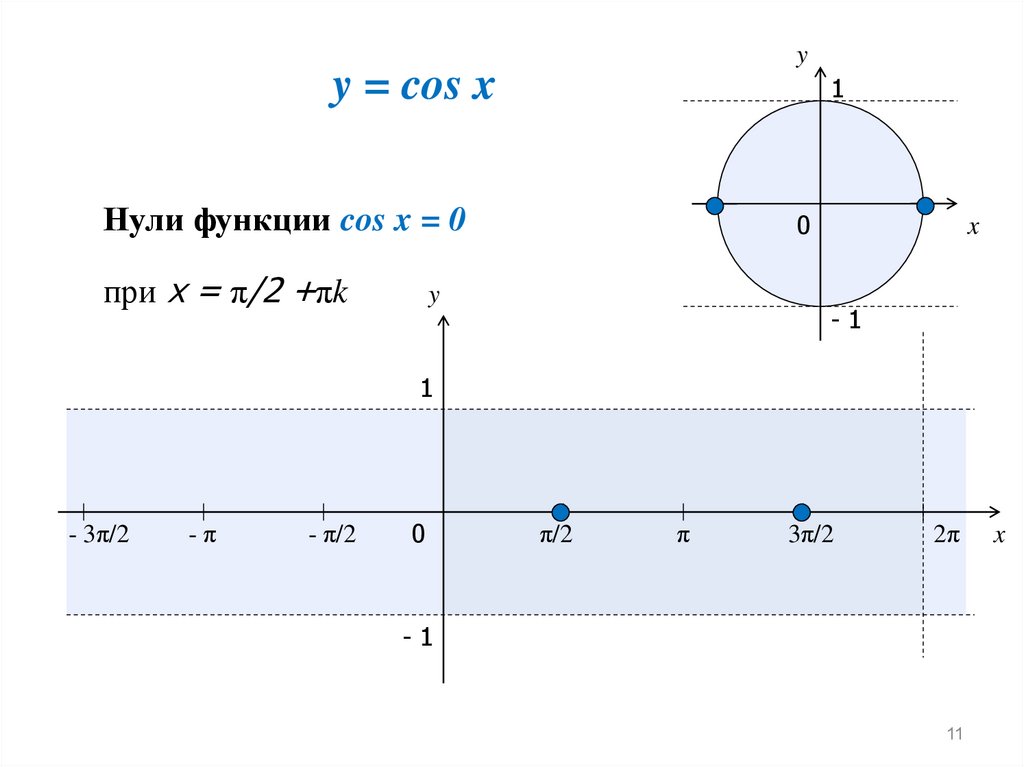
Нули функции cos x = 0
при x = π/2 +πk
0
y
x
-1
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
11
x

12.

y
y = cos x
1
-1
0
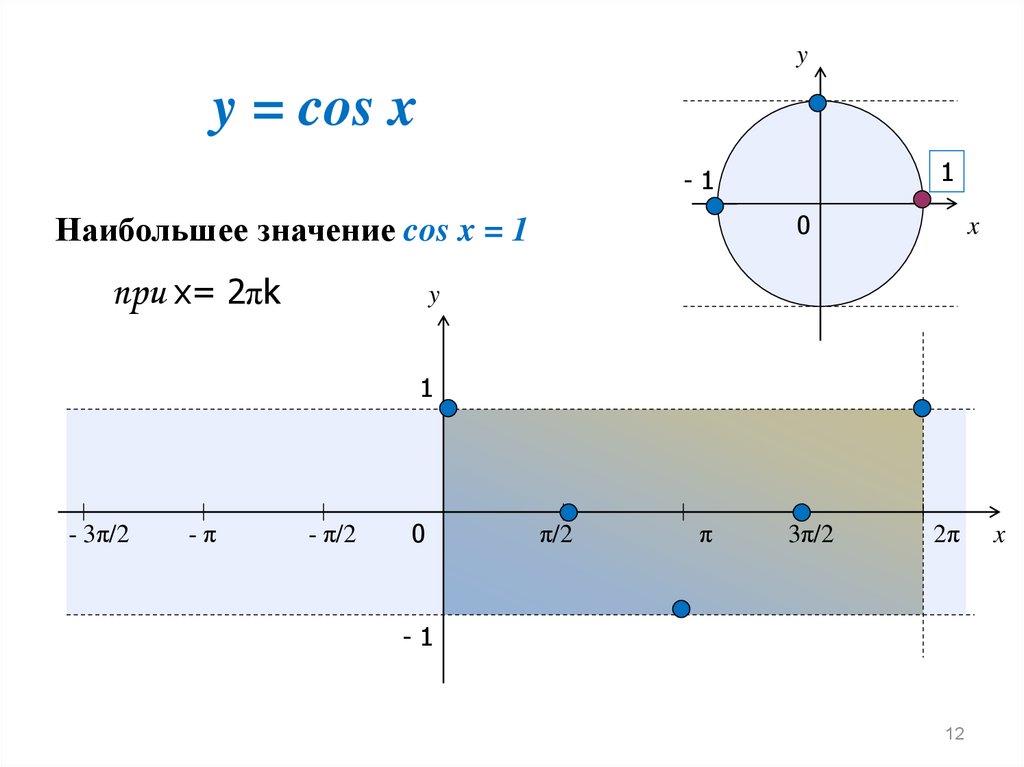
Наибольшее значение cos x = 1
при х= 2πk
x
y
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
12
x

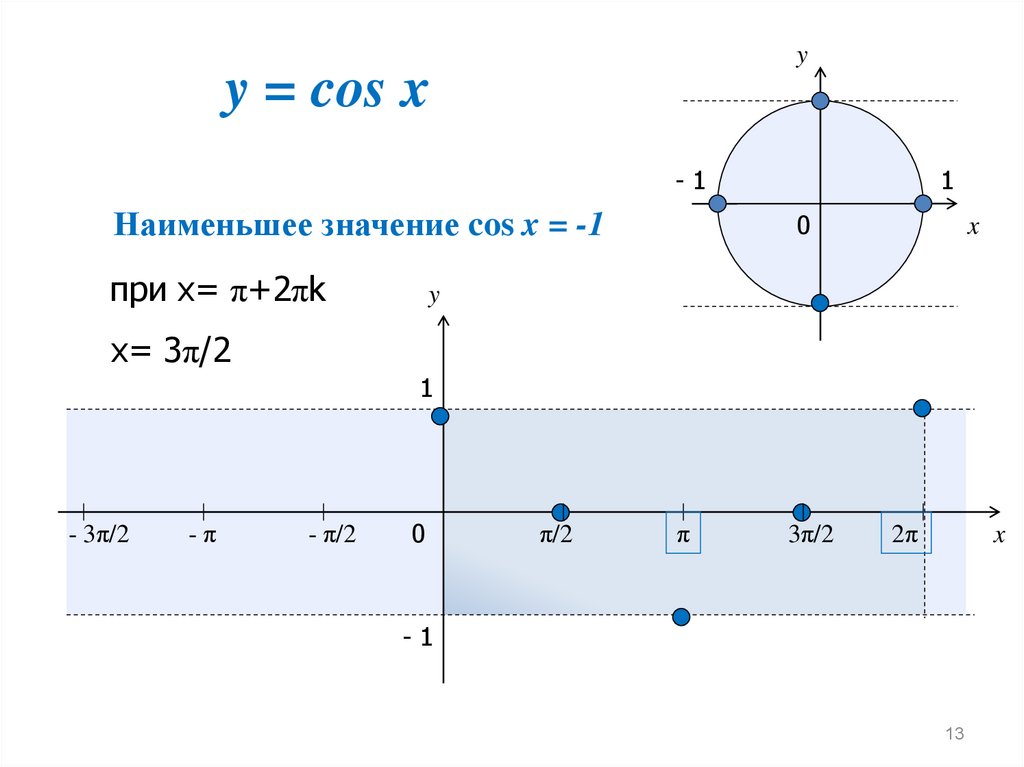
13.

y
y = cos x
-1
Наименьшее значение cos x = -1
при х= π+2πk
1
0
x
y
х= 3π/2
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
x
-1
13

14.

Построение графика функции
y = cos на отрезке
y
0, 2
3
4
6
cos(0)=1
x
cos(π/4) 0,7
y
cos(π/3) 0,5
1
- 3π/2
-π
- π/2
0
6
π/2
4 3
π
3π/2
2π
-1
14
x

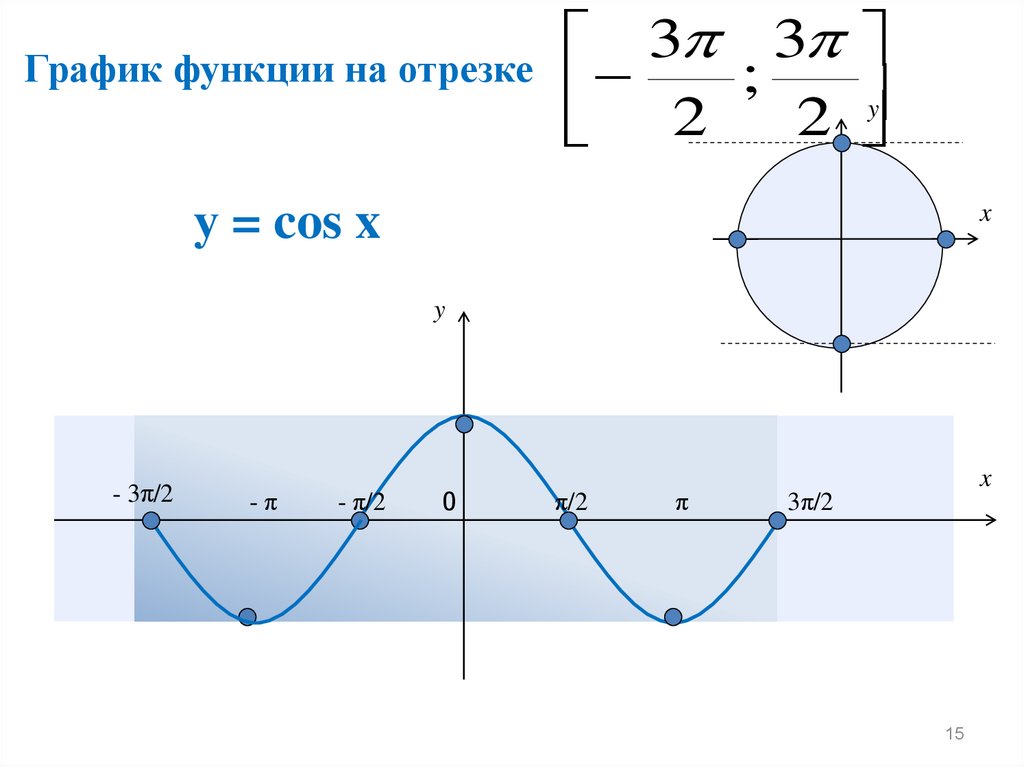
15.

3
3
График функции на отрезке
;
2
2 y
у = cos x
x
y
- 3π/2
-π
- π/2
0
π/2
π
x
3π/2
15

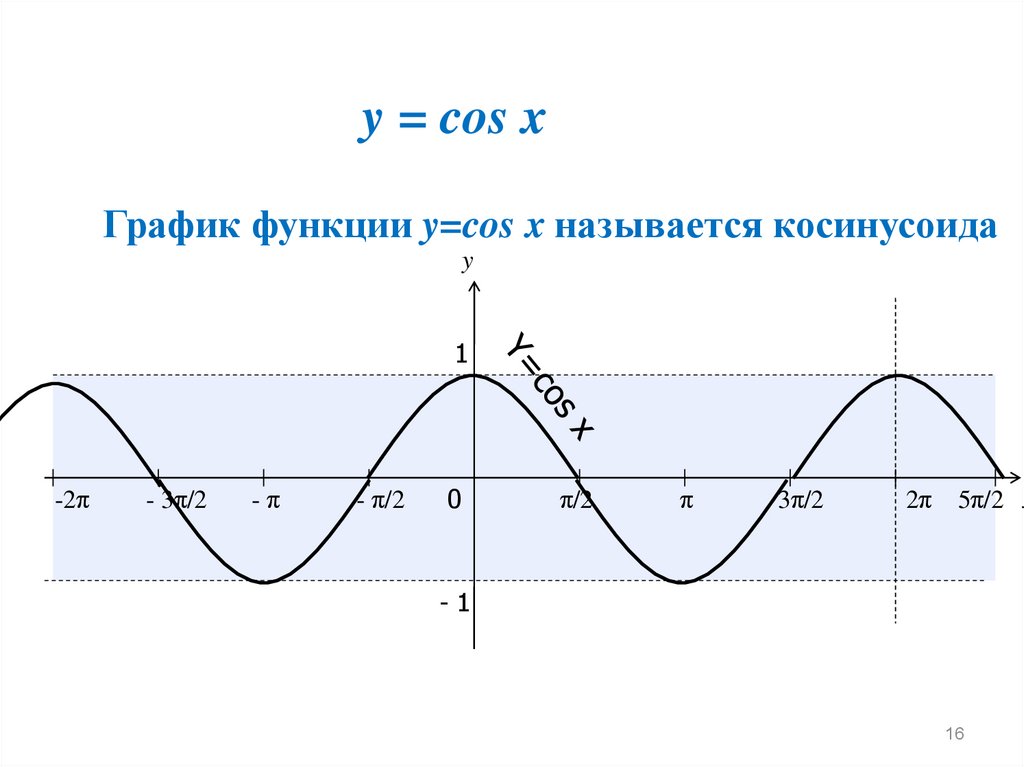
16.

y = cos x
График функции y=cos x называется косинусоида
y
1
-2π
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
5π/2 x
-1
16

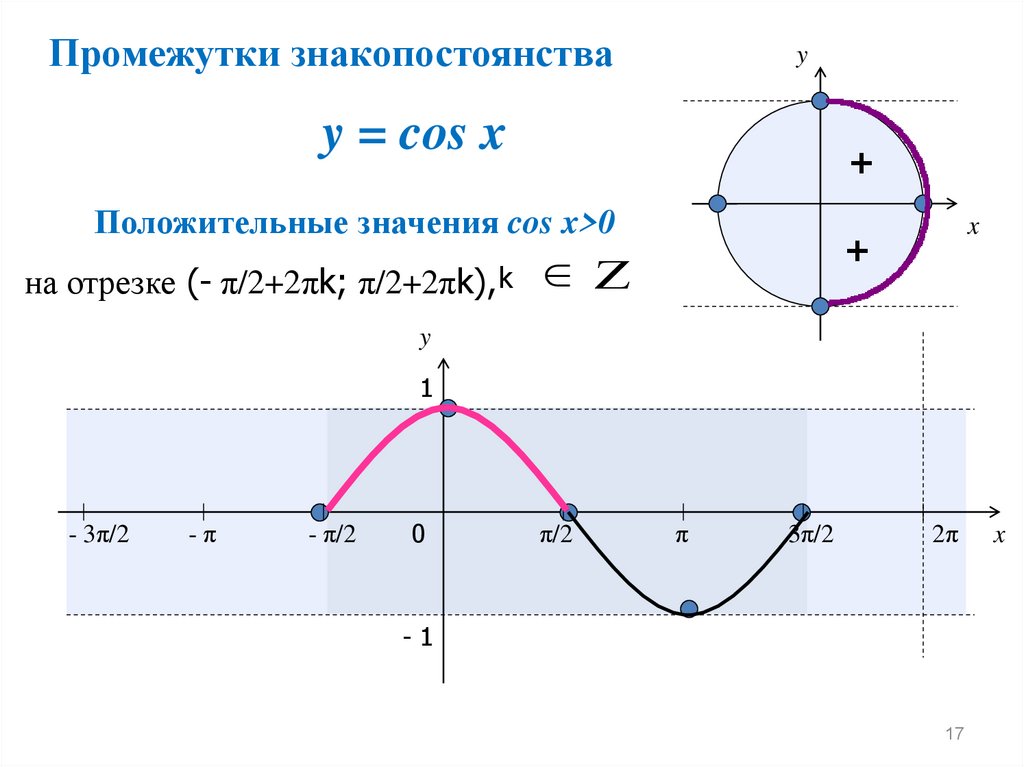
17.

Промежутки знакопостоянства
y
y = cos x
+
Положительные значения cos x>0
на отрезке (- π/2+2πk; π/2+2πk), k
x
+
y
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
17
x

18.

.
y
Промежутки знакопостоянства
y = cos x
–
Отрицательные значения cos x<0
x
–
на отрезке (π/2+2πk; 3π/2+2πk). k
y
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
18
x

19.

Промежутки возрастания
y
y = cos x
Функция возрастает
на отрезке [-π+2πk; 2πk]
x
y
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
x
2π
-1
19

20.

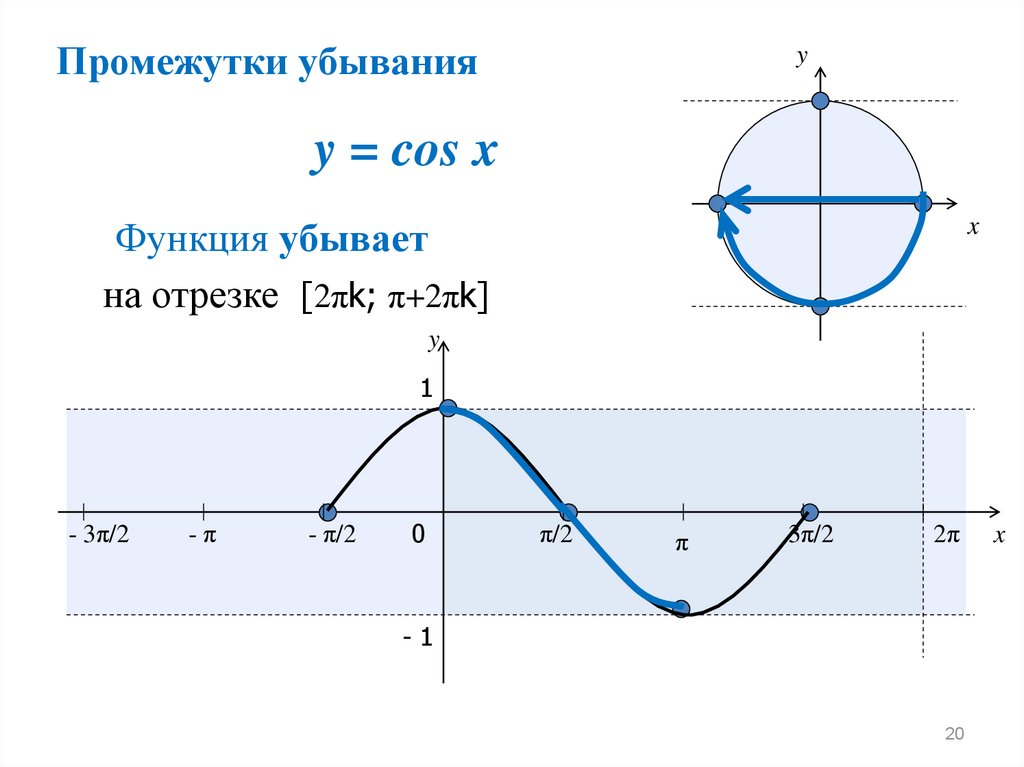
Промежутки убывания
y
y = cos x
Функция убывает
на отрезке [2πk; π+2πk]
x
y
1
- 3π/2
-π
- π/2
0
π/2
π
3π/2
2π
-1
20
x

21.

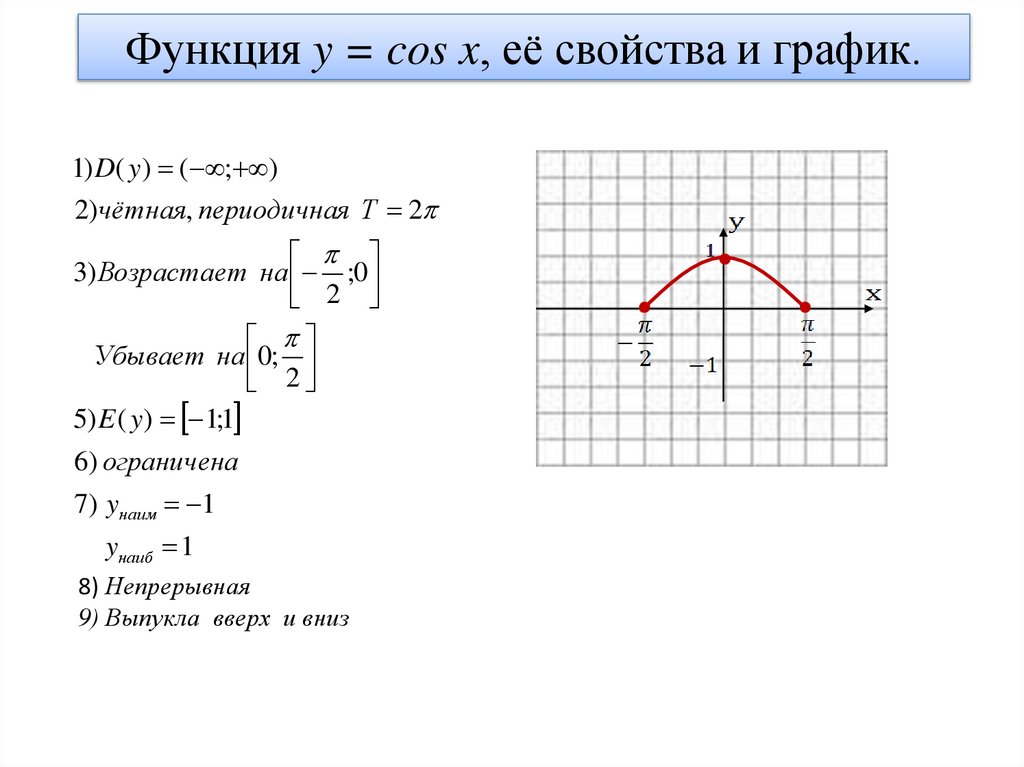
Функция y = cos x, её свойства и график.
1) D( y ) ( ; )
2)чётная, периодичная Т 2
3) Возрастает на ;0
2
Убывает на 0;
2
5) E ( y ) 1;1
6) ограничена
7) yнаим 1
yнаиб 1
8) Непрерывная
9) Выпукла вверх и вниз

22.

y = cos x
у
1
-π/2
-π
π
0
π/2
2π
3π/2
3π
х
5π/2
-1
График функции у=cos x
влево на π/2
получен при смещении синусоиды

23.

y
3
2
y = соs x
-3
2
y = sin x
1
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
х

24.

Некоторые преобразование
Сдвиг вдоль оси ординат
графика
y = cos x
4,5
y = cos x + 3
4
Построить график 3,5
3
функции
2,5
3
2
у=cosх+3
1,5
y = cos x
1
+
0,5
вверх
0
2
-0,5
-1
-1,5
y = cos x
1,5
Построить график
функции
у=cosх-3
1
0,5
0
-0,5
-1
y = cosx - 3
-1,5
-2
-2,5
-3
- вниз
-3,5
-3
-4
-4,5
24

25.

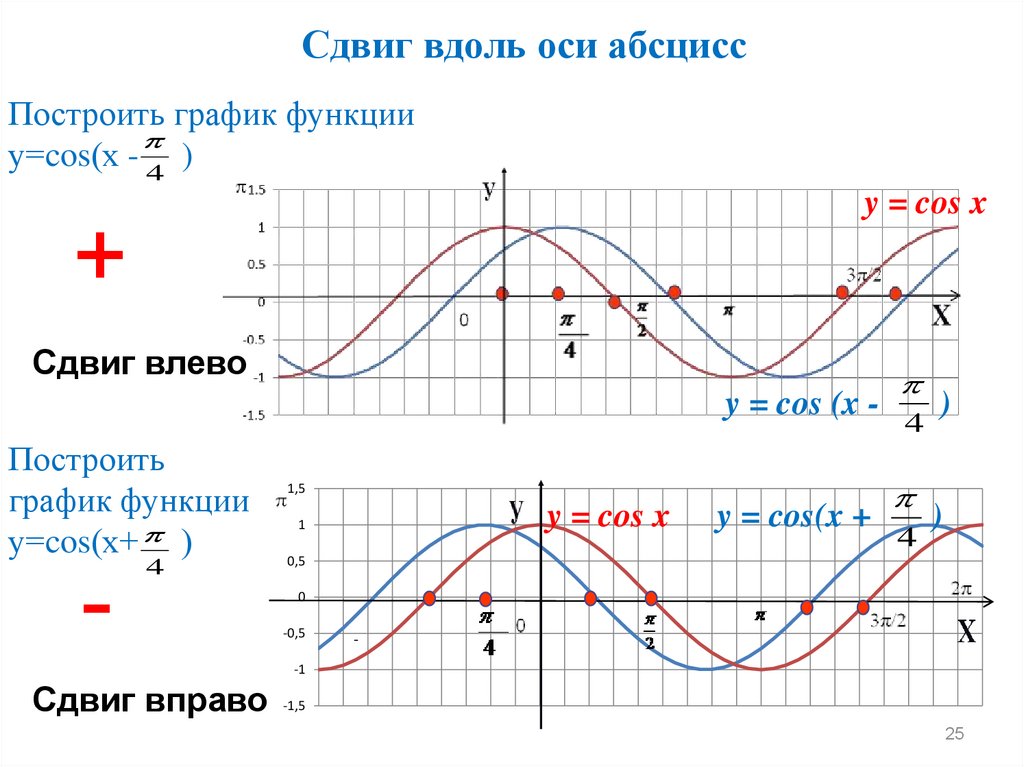
Сдвиг вдоль оси абсцисс
Построить график функции
у=cos(х - 4 )
y = cos x
+
Сдвиг влево
y = cos (x Построить
график функции
у=cos(х+ )
-
4
1,5
y = cos x
1
y = cos(x +
4
4
)
)
0,5
0
-0,5
-
-1
Сдвиг вправо -1,5
25

26.

Сжатие и растяжение к оси абсцисс
Построить график
функции у= 3 cosх
y = 3 cos x
y = cos x
K >1
растяжение
Построить график
функции у=1/ 3 cosх
y = cos x
у = 1/3 cos x
0< K <1
сжатие
26

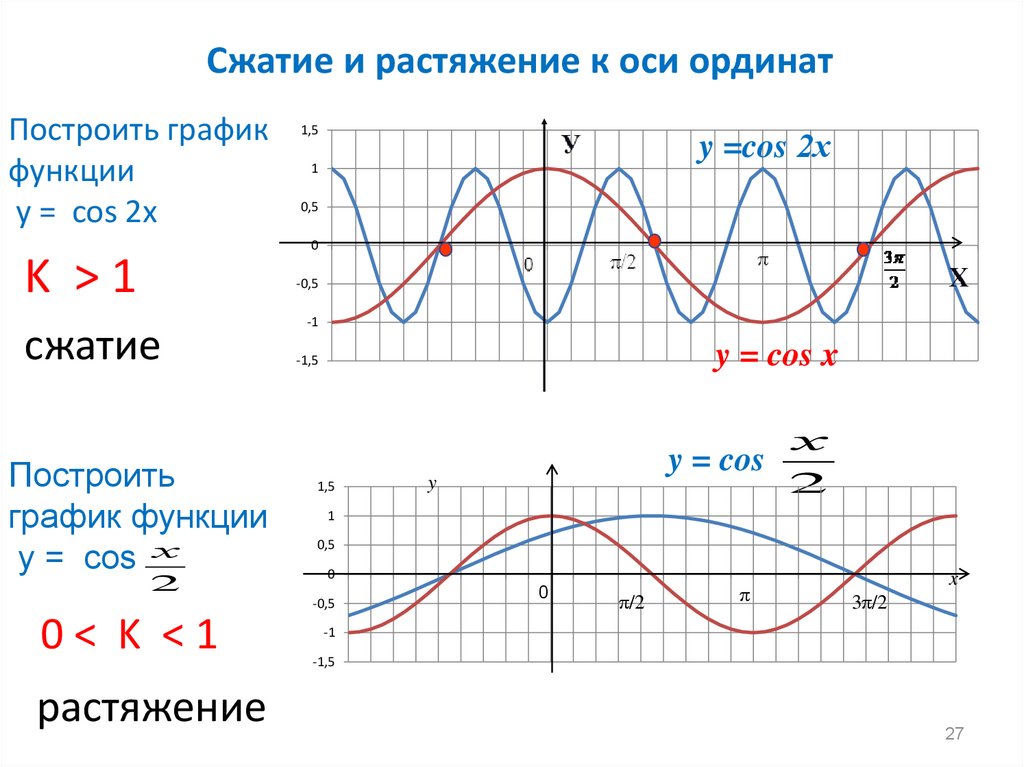
27.

Сжатие и растяжение к оси ординат
Построить график
функции
у = cos 2х
1,5
y =cos 2х
1
0,5
0
K >1
-0,5
сжатие
Построить
график функции
у = cos х
2
-1
y = cos x
-1,5
1,5
растяжение
y
х
2
1
0,5
0
-0,5
0< K <1
y = cos
0
π/2
π
x
3π/2
-1
-1,5
27

28.

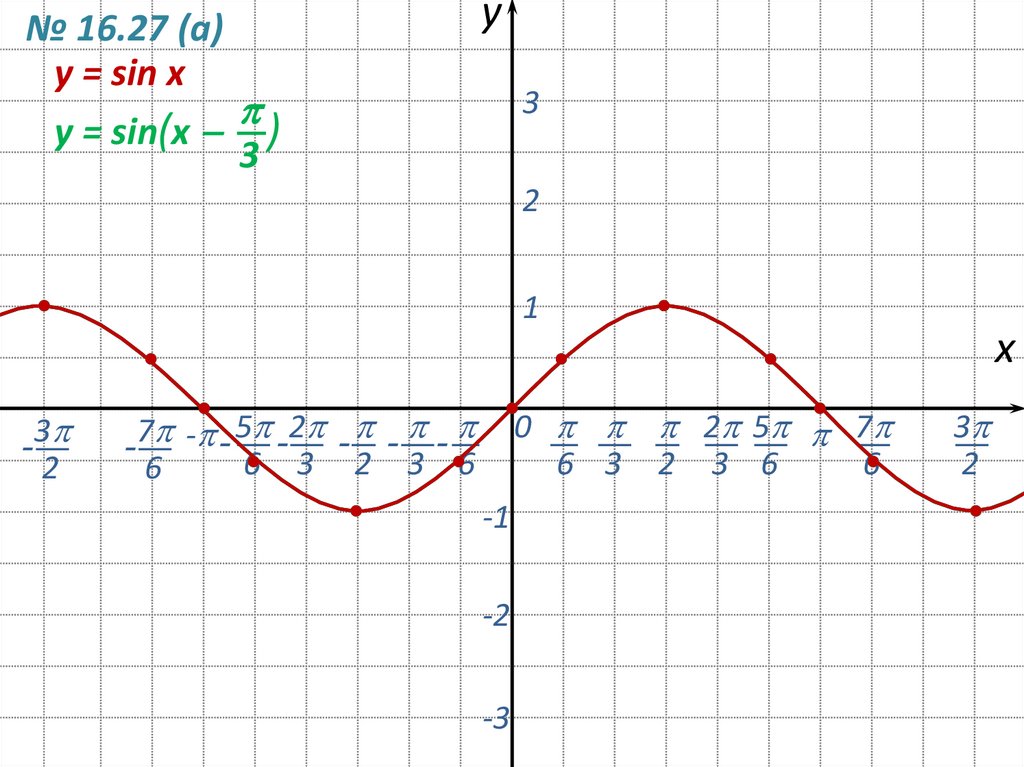
№ 16.27 (а)
y = sin x
y = sin(x )
3
y
3
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2

29.

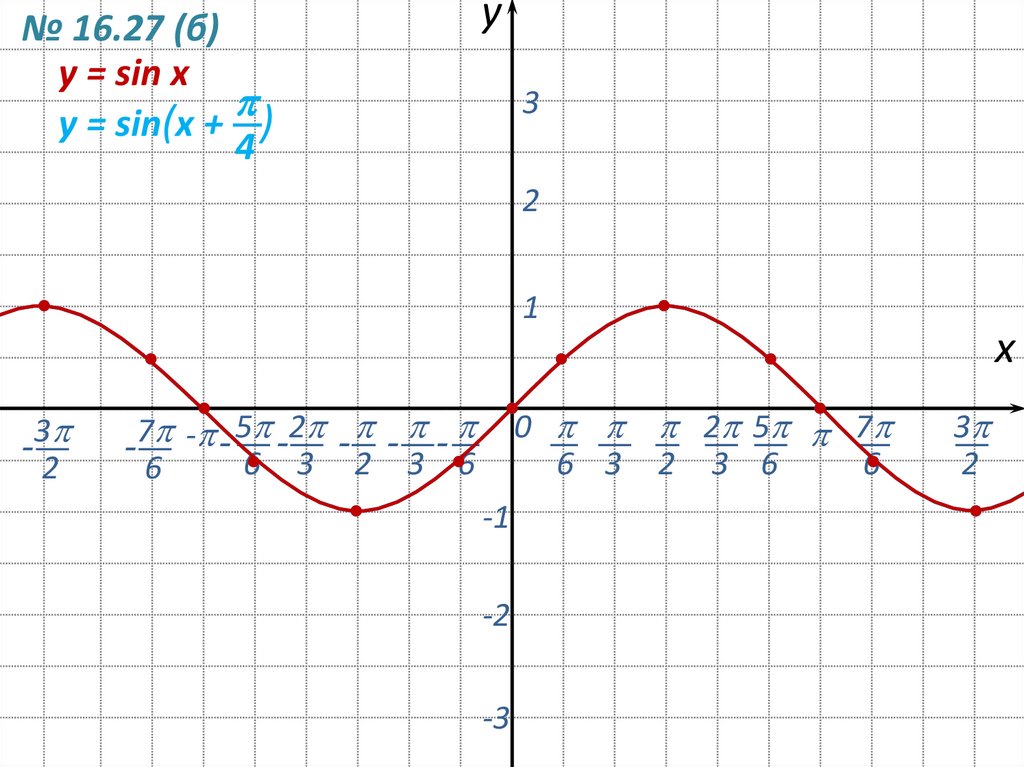
№ 16.27 (б)
y = sin x
y = sin(x + )
4
y
3
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2

30.

№ 16.28 (а)
y = sin x
y = sin x 2
y
3
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2

31.

№ 16.28 (б)
y = sin x
y = sin x + 1
y
3
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2

32.

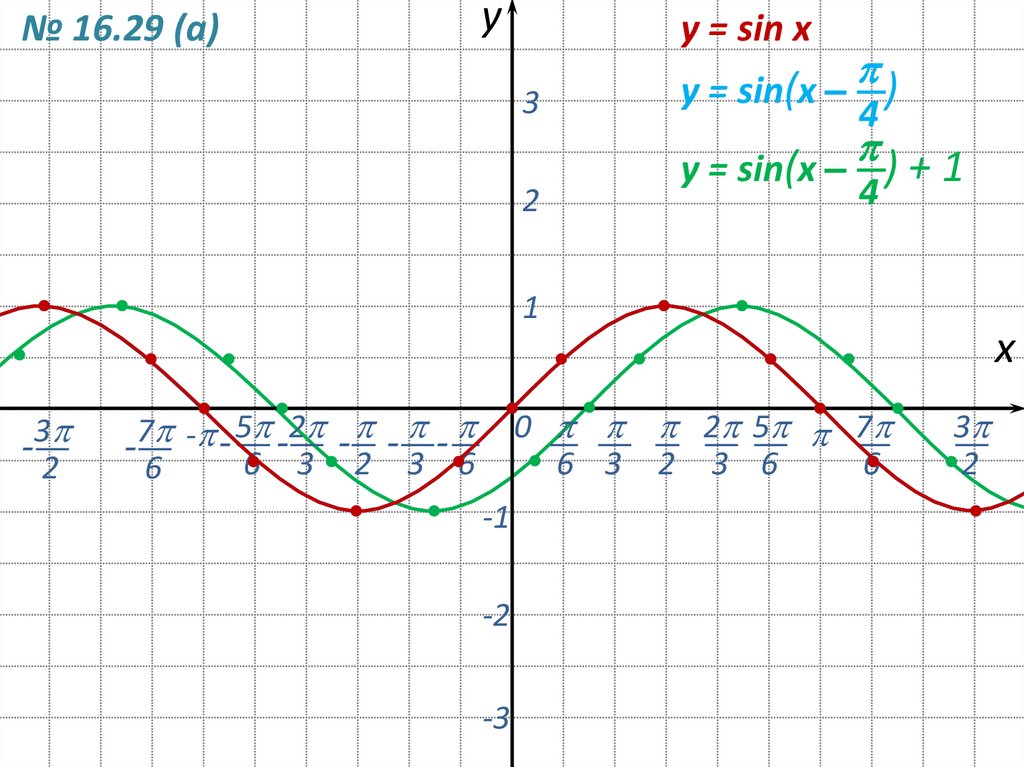
№ 16.29 (а)
y
y = sin x
y = sin(x – )
4
y = sin(x – ) + 1
4
3
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2

33.

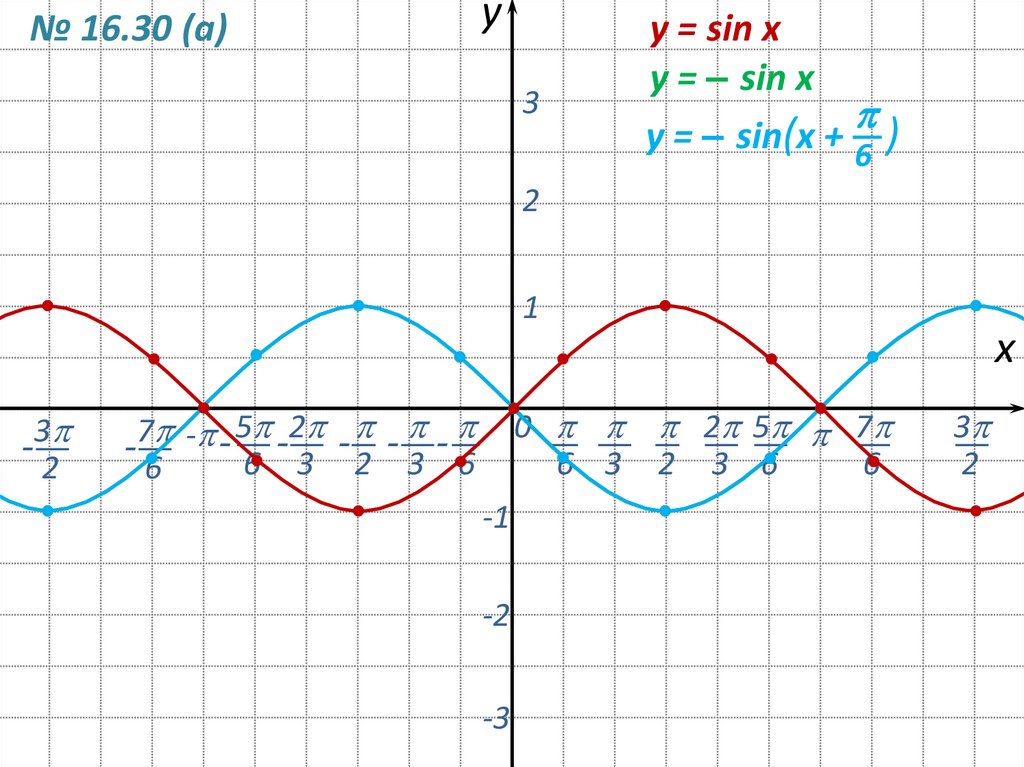
№ 16.30 (а)
y
3
y = sin x
y = – sin x
y = – sin(x + 6 )
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2

34.

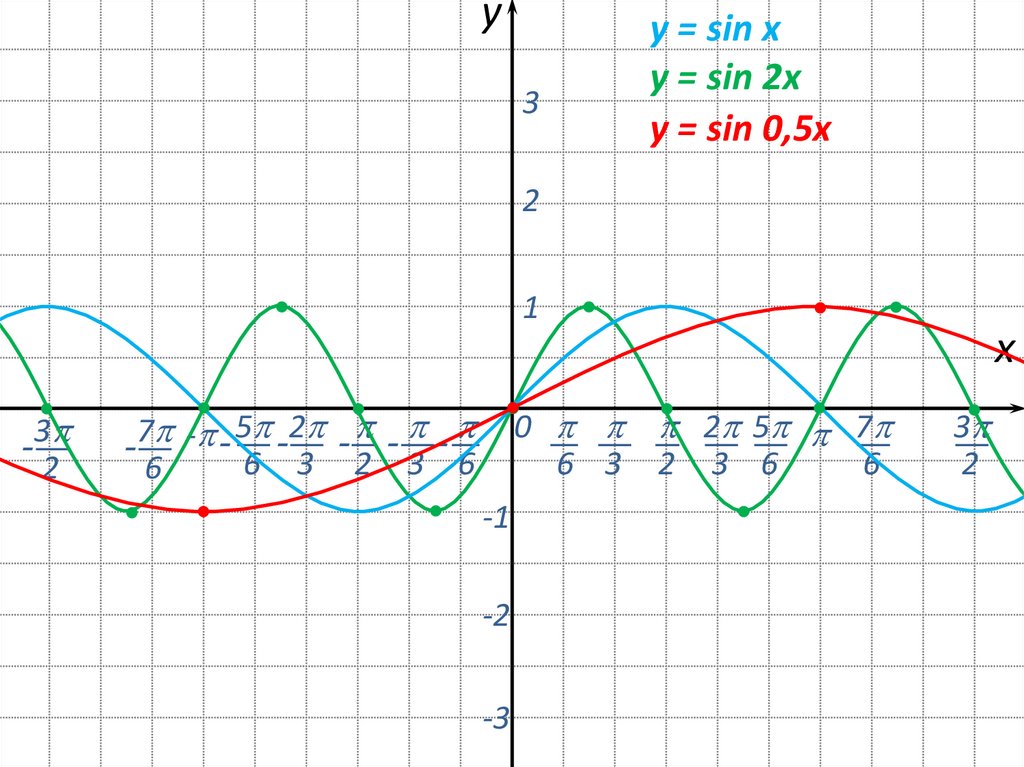
y
3
y = sin x
y = sin 2x
y = sin 0,5x
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2

35.

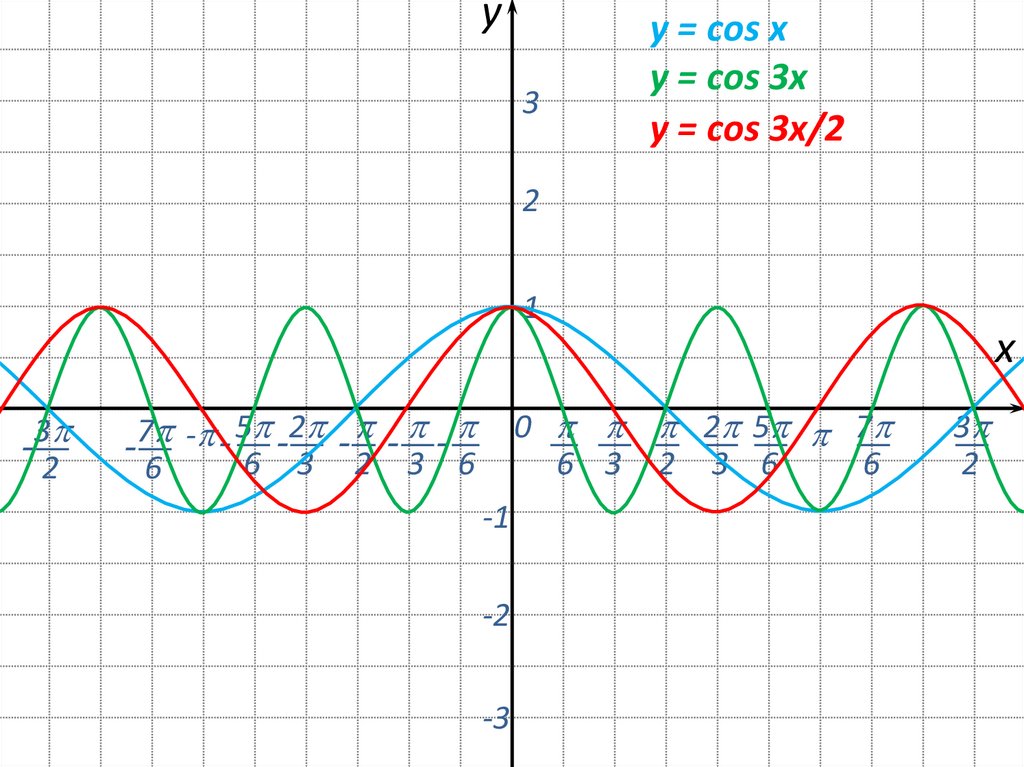
y
3
y = соs x
y = соs 3x
y = соs 3x/2
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2

36.

y
3
y = 3sin x
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
y = sinx
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2