Синус, косинус, тангенс гострого кута прямокутного трикутника

1.

Епіграф до уроку
Природа
формує свої
закони мовою
математики.
Г.Галілей

2.

3.

Дитяча школа Гауді в Барселоні

4.

5.

6.

7.

Тригонометрія у перекладі з грецької означає
«вимірювання трикурників» Тригонометрія (від
грец. trigwnon - трикутник и metrew - виміряю)
Тригонометрія була викликана до життя
необхідністю вимірювати кути.
Першими кроками тригонометрії було
встановлення зв’язків між величиною кута та
відношенням специально побудованих відрізків
прямих.

8.

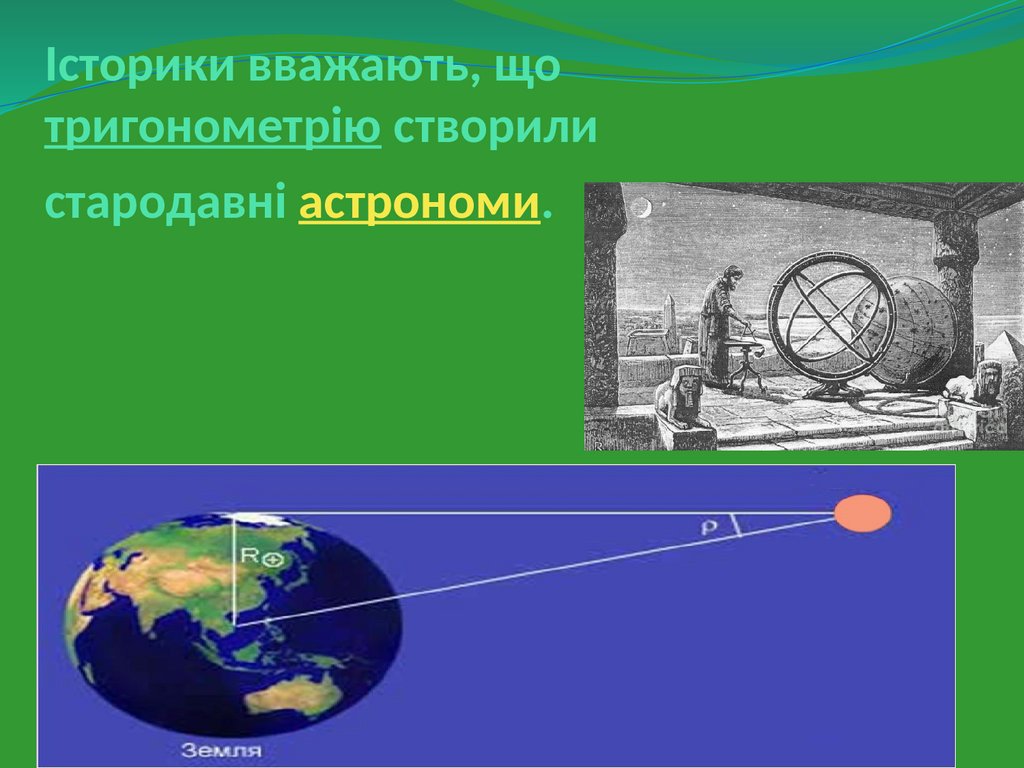
Історики вважають, що
тригонометрію створили
стародавні астрономи.

9.

історія тригонометрії
За допомогою зірок
обчислювали
місцезнаходження
корабля в морі.
Давні люди обчислювали
висоту дерева,
порівнюючи довжину
його тіні з довжиною тіні
від шеста, висота якого
була відома.

10.

За допомогою
співвідношень
між кутами та
сторонами
прямокутного
трикутника люди
вимірювали
висоту споруд.
С
А
Н

11.

Синус, косинус,
тангенс гострого
кута
прямокутного
трикутника

12.

13.

B
BC
sin A
AB
AC
cos A
AB
BC
tg A
AC
C
A
sin B ?
cos B ?
tg B ?

14.

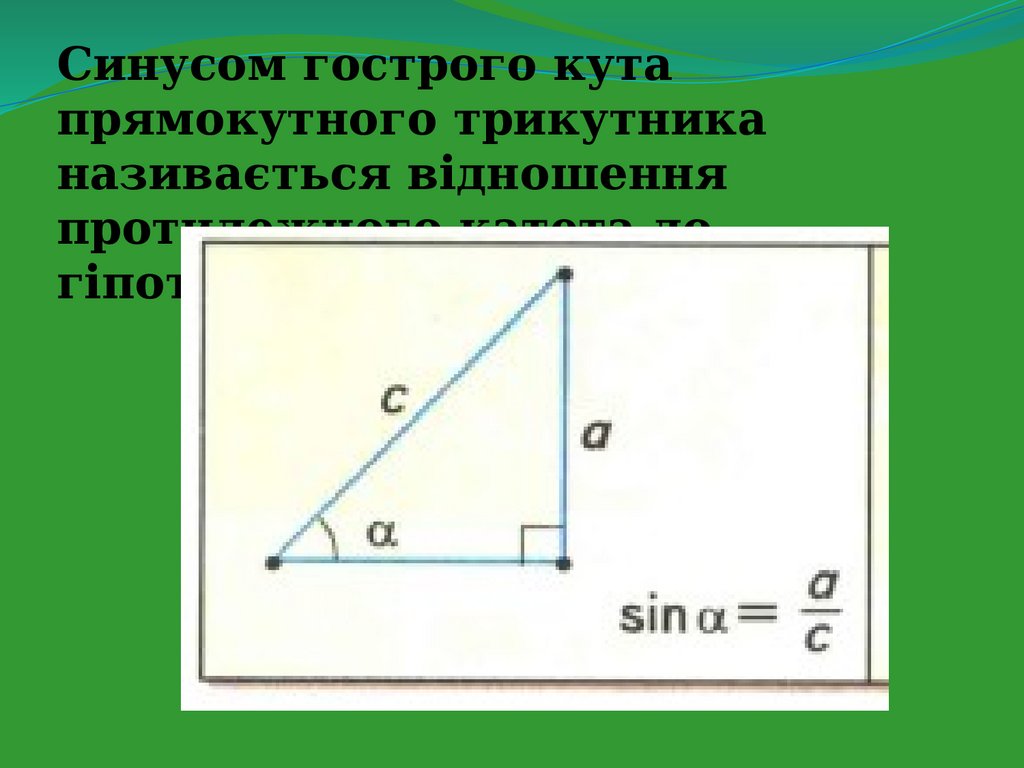
Синусом гострого кута
прямокутного трикутника
називається відношення
протилежного катета до
гіпотенузи.

15.

Історія синусів
Індійськіські математики слово синус
записали як «джива» - тятива лука.
Арабські математики переводити з
індійської мови не захотіли і записав його
по буквам «д-ж-и-в-а». Потім подумали:
«Що тут написано? «Джиба»? Мабуть
«Джайб»?» «Джайб» - це пазуха.
Європейські математики слово пазуха
перевели на латинь як синус (впадина,
кривизна).
Помилку помітили лине в 19 сторіччі, але
міняти нічого не стали. Адже це нікому не
заважало.

16.

Видатний індійський астроном і
математик АРІАБХАТА вперше
ввів потяття «джива»
Пам'ятник
Аріабхаті на
території
університету
в Пуне

17.

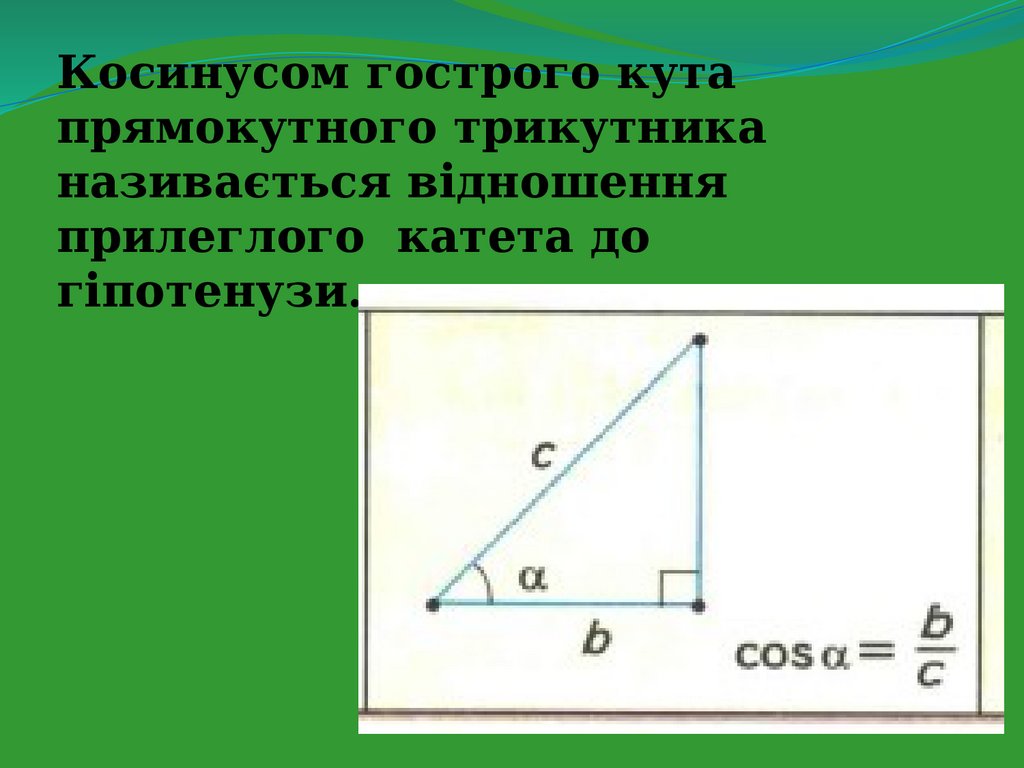
Косинусом гострого кута
прямокутного трикутника
називається відношення
прилеглого катета до
гіпотенузи.

18.

Косинус – від
латинського
«компліментарі синус» додатковий синус.

19.

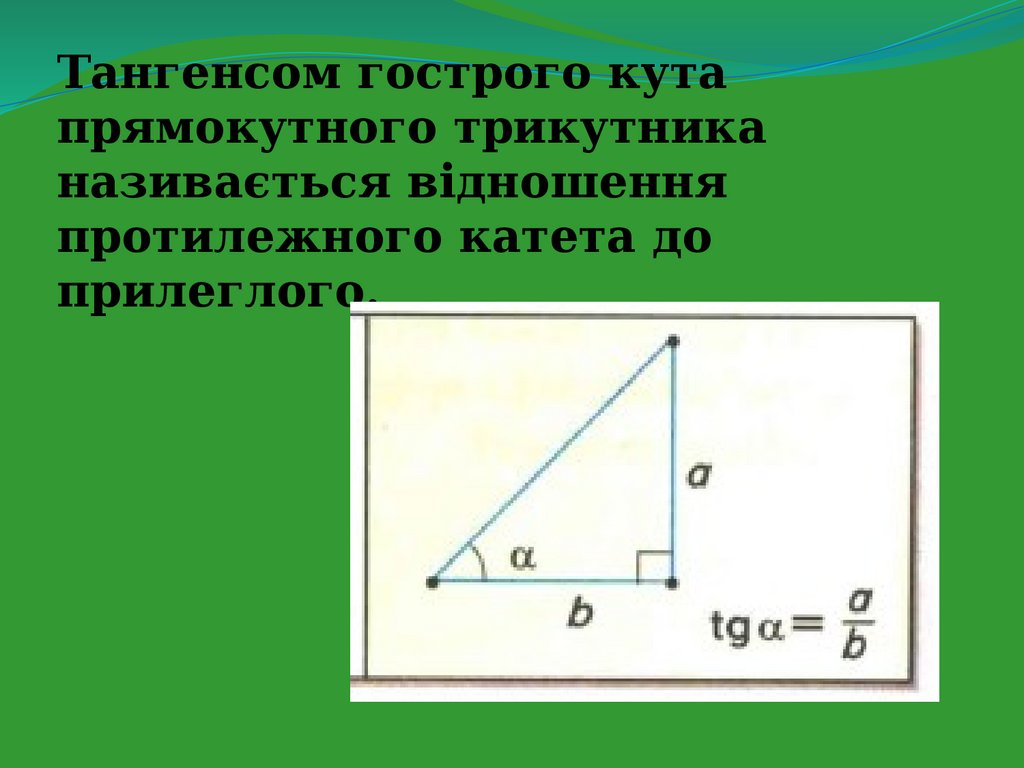
Тангенсом гострого кута
прямокутного трикутника
називається відношення
протилежного катета до
прилеглого.

20.

Тангенс – у перекладі з латинської
«дотичний»
Сучасні позначення sin, cos, tg уперше застосував
швейцарський математик Й. Бернулі в листі до
Леонарда Ейлера (1739).
Ейлер визнав їх найзручнішими. Авторитет Ейлера
сприяв тому, що ці позначення стали
загальноприйнятими.

21.

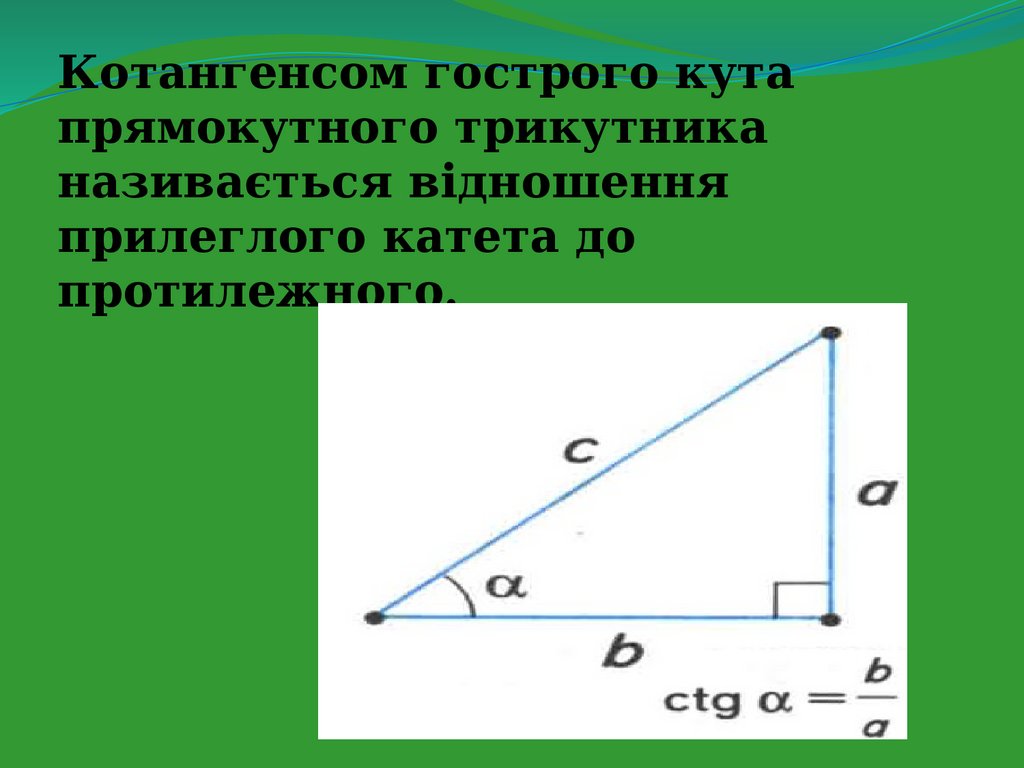
Котангенсом гострого кута
прямокутного трикутника
називається відношення
прилеглого катета до
протилежного.

22.

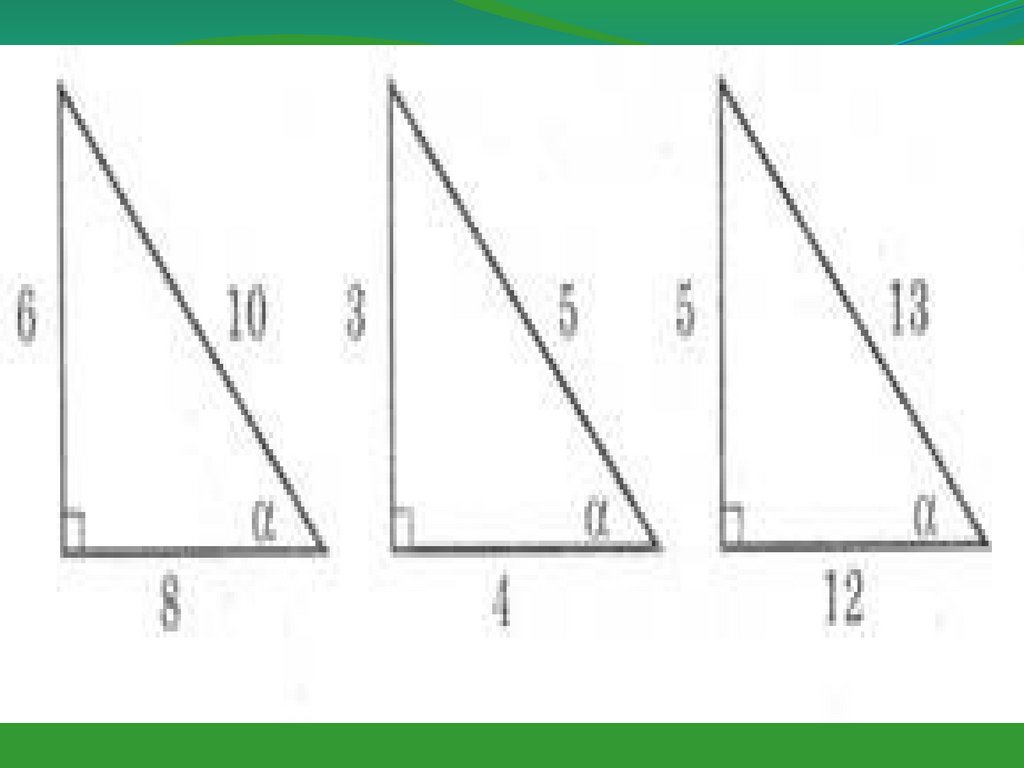
Розв’язування задач
(усно)

23.

24.

25.

26.

Побудова кута за його
тригонометричними функціям
и

27.

Побудова кута за його тригонометричними
функціями
3
Задача 1. Побудувати кут, синус якого
5
дорівнює
Побудова
За допомогою довільного розхилу циркуля
будуємо два відрізки 3:5.
3
5
Кут α - шуканий кут
5
3
α
Будуємо прямокутний трикутник за даною
гіпотенузою та катетом

28.

Побудова кута за його тригонометричними
функціями
5
Задача 1. Побудувати кут, тангенс якого
4
дорівнює
Побудова
За допомогою довільного розхилу циркуля
будуємо два відрізки 4:5.
4
5
α
Кут α - шуканий кут
4
5
Будуємо прямокутний трикутник за
даними катетами

29.

Розмірковуємо
1. Чи правильна нерівність sinα > 1?
Відповідь пояснити.
2. Чи правильна нерівність cosα > 1?
Відповідь пояснити.
3. Чи правильна нерівність tgα > 1?
Відповідь пояснити.
Висновок
Значення sinα , cosα не може бути більше
одиниці, тому, що катет завжди менший від
гіпотенузи.
Значення tgα , сtgα може бути більше
одиниці і менше одиниці, тому, що катети
можуть бути і менше і більше один одного.

30.

Розв’язування задач
Задача 1.
Знайдіть синус, косинус,
тангенс найменшого кута
єгипетського трикутника.

31.

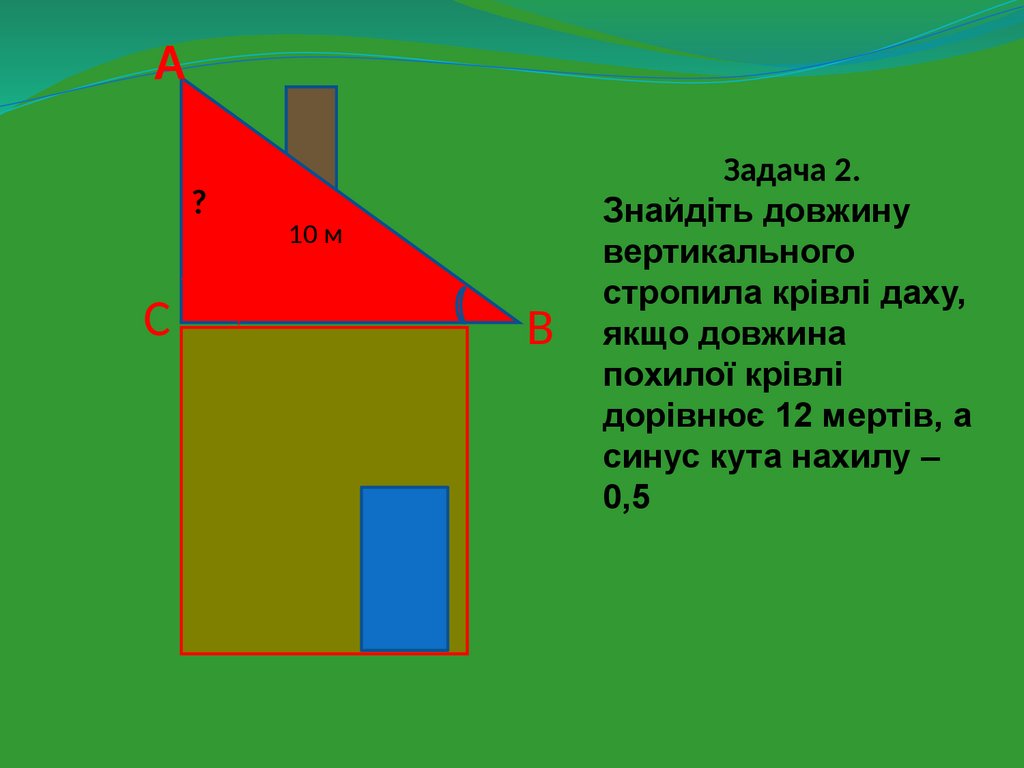
А
?
С
10 м
В
Задача 2.
Знайдіть довжину
вертикального
стропила крівлі даху,
якщо довжина
похилої крівлі
дорівнює 12 мертів, а
синус кута нахилу –
0,5

32.

Розв’язування задач
Задача 3. (№ 668)
Катети прямокутного
трикутника дорівнюють 8см і
15 см. Обчисліть синус, косинус
і тангенс найменшого кута
трикутника.

33.

Розв’язування задач
Задача 4 .
У прямокутному трикутнику
АВС ( кут С = 900) катет а=5
см, гіпотенуза с = 13 см.
Знайдіть синус, косинус,
тангенс кута В.

34.

Розв'язування вправ. Робота з
підручником. (стр. 177)
Розв'язання
BC
8
sin
; sin 0,5;
AВ
17
AС
cos
;
AВ
15
cos 0,9;
17
BC
tg
,
AС
8
tg 0,5.
15

35.

Рефлексія

36.

За допомогою графіків синуса та
косинуса описується робота
серця людини.

37.

Рух риб у воді
відбувається за законом
синуса або косинуса.
Під час плавання тіло
риби приймає форму
схожу на графік
тангенса

38.

Під час польоту птаха траекторія помаху крил нагадує
графік синуса

39.

Теорія Веселки
Веселка виникає в результаті того, що
сонячне світло зазнає заломлення в
крапельках води, зважених у повітрі за
законом заломлення:
n1 – показник заломлення першого
середовища
n2 – показник заломлення другого
середовища
α-кут падіння, β-кут заломлення світла
sin α / sin β = n1 / n2

40.

Крівля дитячої школи Гауді в Барселоні
нагадує графіки синуса або косинуса

41.

42.

Домашнє завдання
Домашнє завдання
Опрацювати параграф 19.1
Розв'язати:
№665 (середній рівень)
№ 667 (достатній рівень)
№676 (високий рівень)

43.

Дякую за
співпрацю!