Похожие презентации:
Тригонометричні функції числового аргументу. Означення синуса, косинуса, тангенса і котангенса кутів повороту. Урок 1-2
1. Урок 1-2 Тригонометричні функції числового аргументу.Означення синуса, косинуса, тангенса і котангенса кутів повороту.
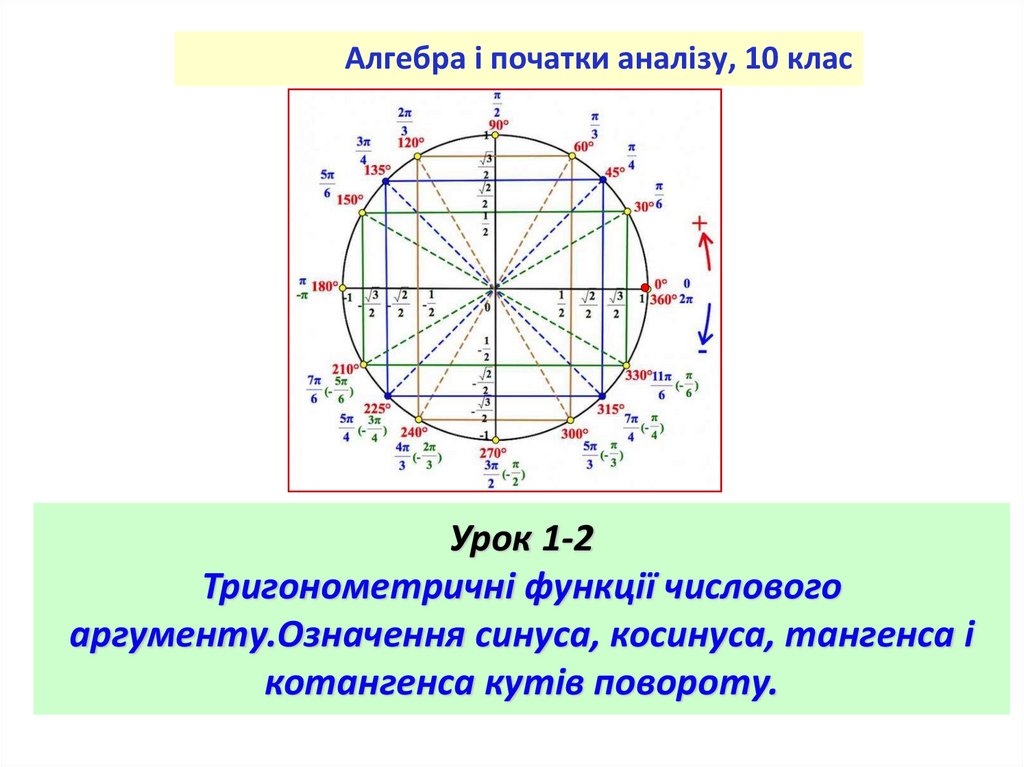
Алгебра і початки аналізу, 10 класУрок 1-2
Тригонометричні функції числового
аргументу.Означення синуса, косинуса, тангенса і
котангенса кутів повороту.
2.
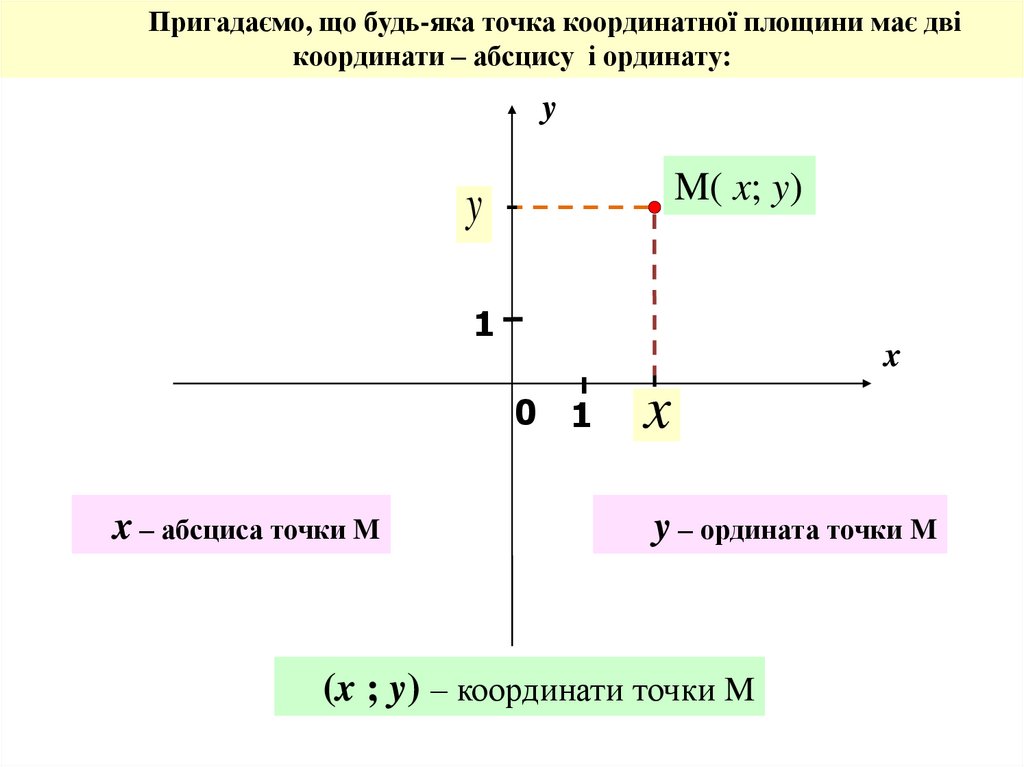
Пригадаємо, що будь-яка точка координатної площини має двікоординати – абсцису і ординату:
y
M( x; y)
y
1
x
0 1
x – абсциса точки M
x
y – ордината точки M
(x ; y) – координати точки M
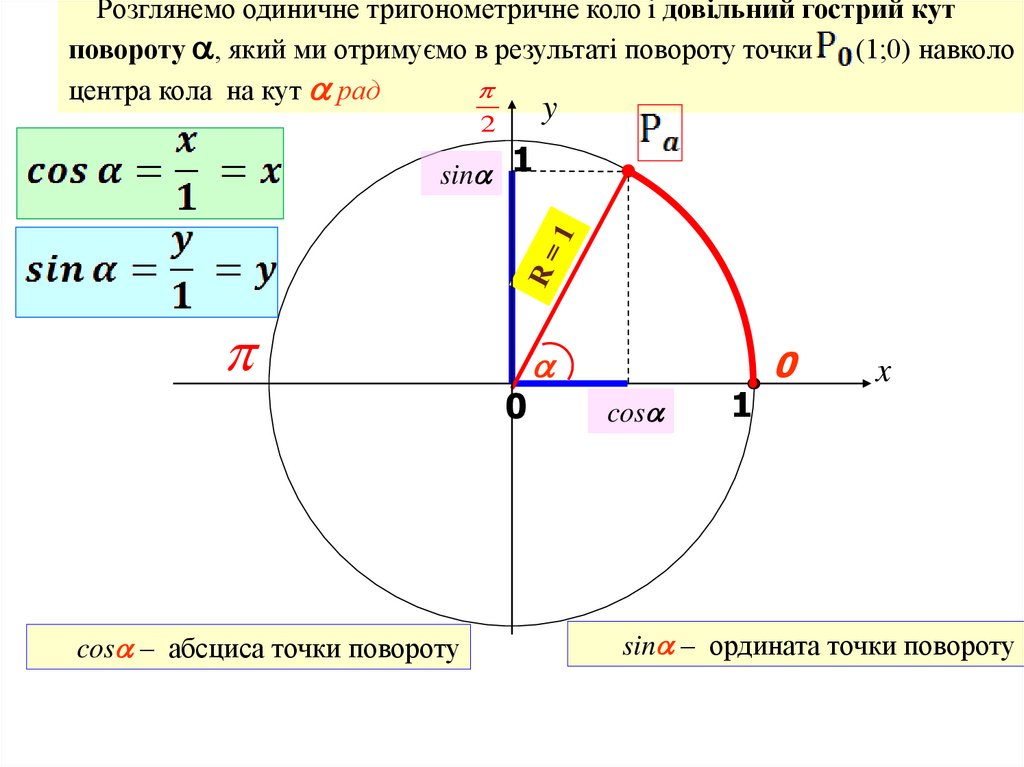
3.
Розглянемо одиничне тригонометричне коло і довільний гострий кутповороту , який ми отримуємо в результаті повороту точки (1;0) навколо
центра кола на кут рад
y
2
sin 1
0
cos – абсциса точки повороту
cos
1
0
x
sin – ордината точки повороту
4.
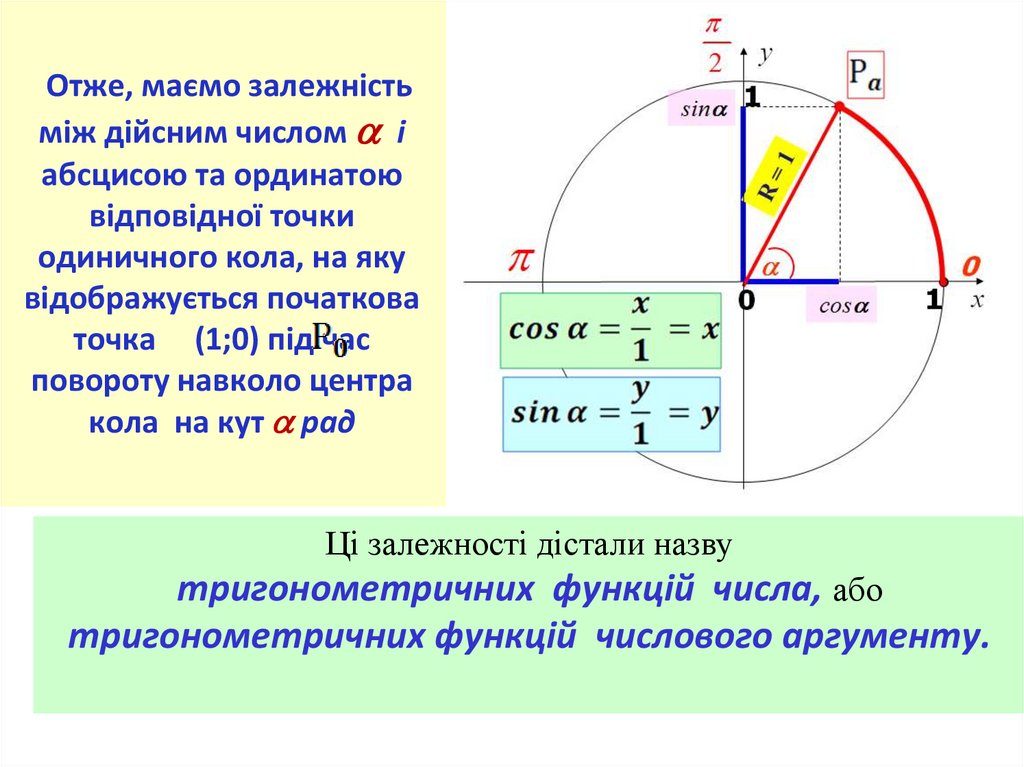
Отже, маємо залежністьміж дійсним числом і
абсцисою та ординатою
відповідної точки
одиничного кола, на яку
відображується початкова
точка (1;0) під час
повороту навколо центра
кола на кут рад
Ці залежності дістали назву
тригонометричних функцій числа, або
тригонометричних функцій числового аргументу.
5.
Синусом числа називаєтьсяордината точки
одиничного кола, в яку
переходить початкова точка (1;0) під час
повороту навколо центра кола на кут
рад, і позначається sin .
Косинусом числа називається абсциса точки
одиничного кола, в яку переходить початкова точка
(1;0) під час повороту навколо центра кола на
кут рад, і позначається cos .
Тангенсом числа називається відношення
а
котангенсом числа відношення
, і позначаються вони
відповідно tg і ctg .
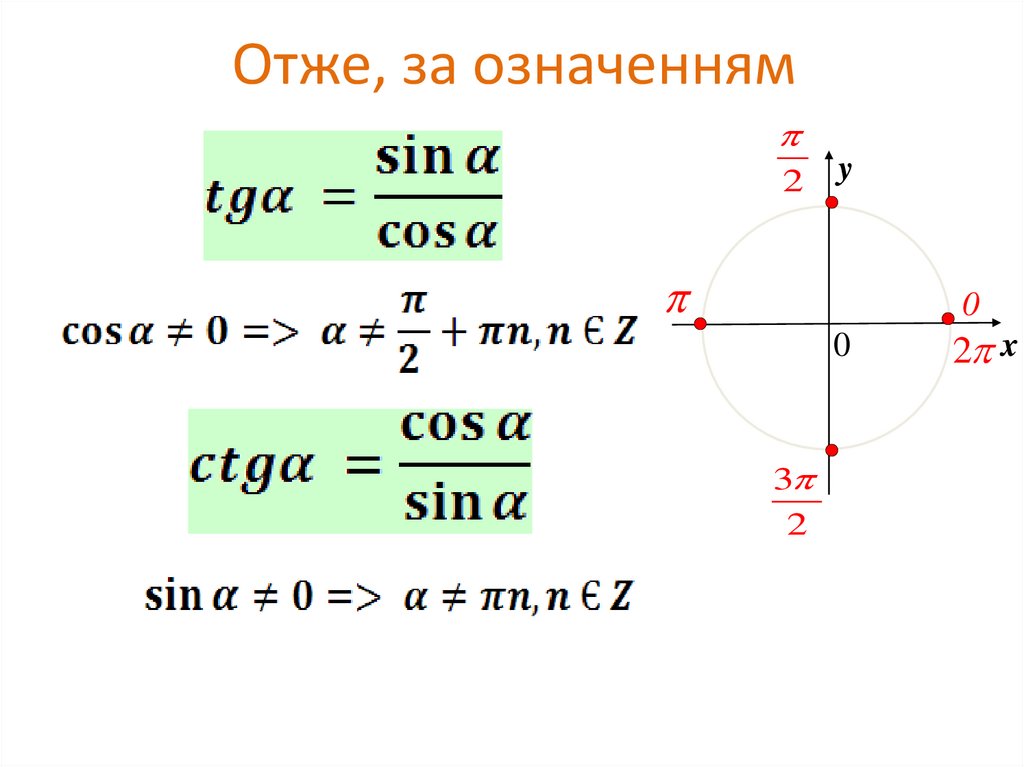
6. Отже, за означенням
2y
0
0
3
2
2 x
7.
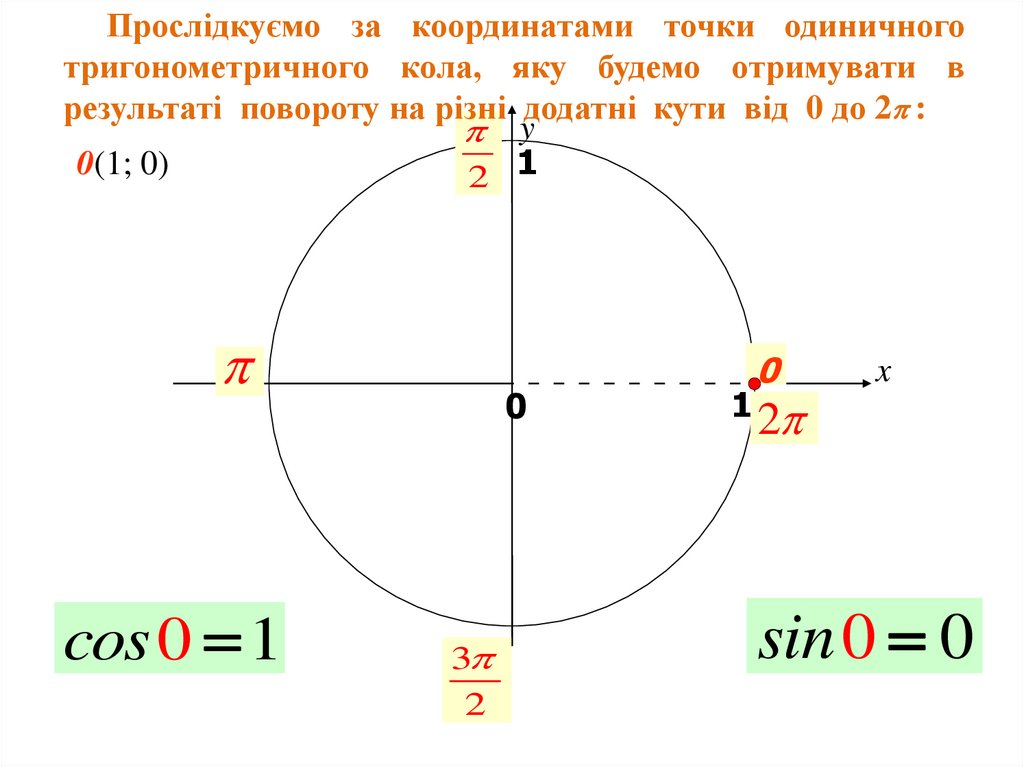
Прослідкуємо за координатами точки одиничноготригонометричного кола, яку будемо отримувати в
результаті повороту на різні додатні кути від 0 до 2 :
y
0(1; 0)
2 1
cos 0 1
0
3
2
1
0
2
x
sin 0 0
8.
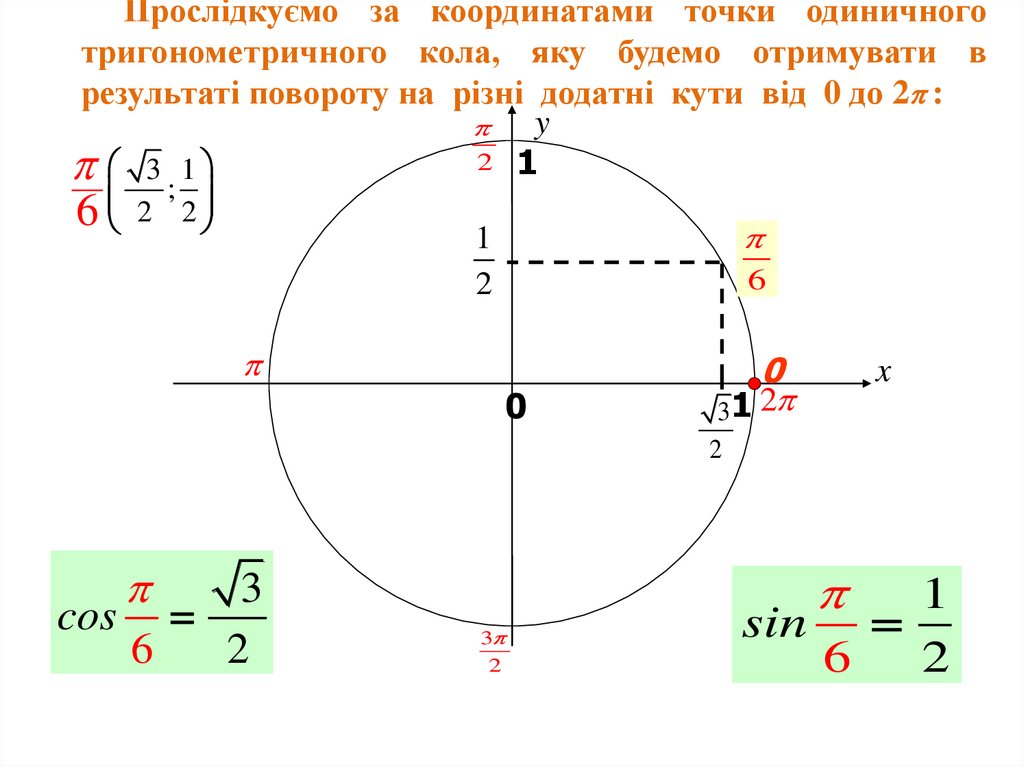
Прослідкуємо за координатами точки одиничноготригонометричного кола, яку будемо отримувати в
результаті повороту на різні додатні кути від 0 до 2 :
y
2 1
3 1
;
6 2 2
1
2
6
0
0
3 1 2
x
2
3
cos
6
2
3
2
1
sin
6
2
9.
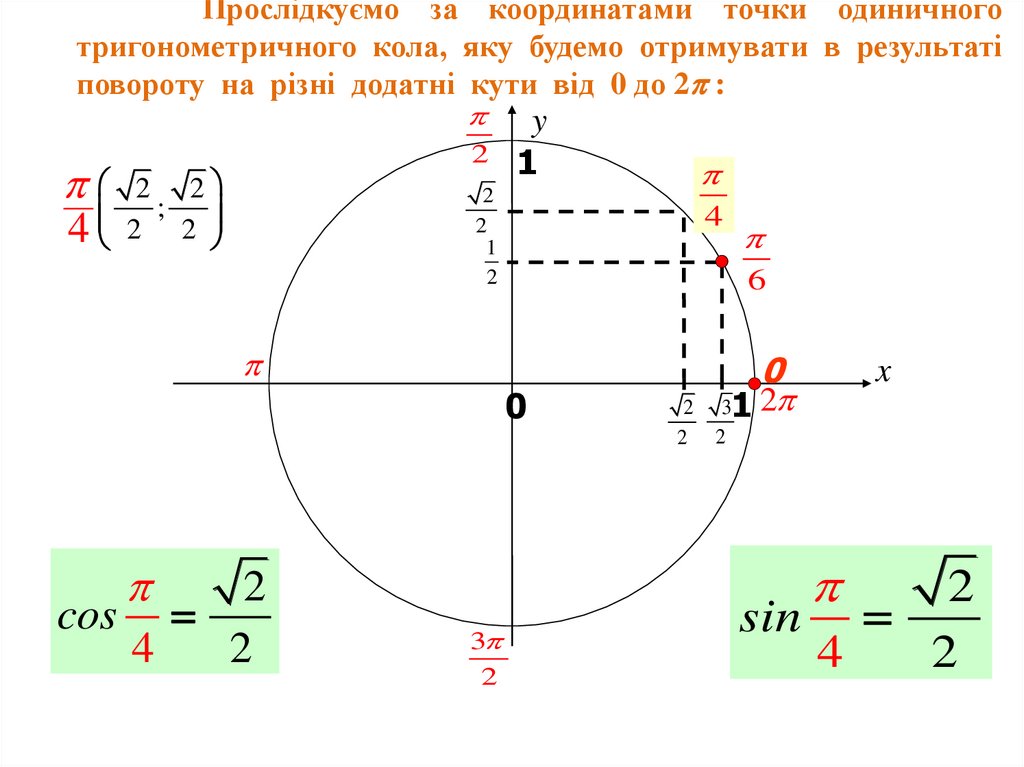
Прослідкуємо за координатами точки одиничноготригонометричного кола, яку будемо отримувати в результаті
повороту на різні додатні кути від 0 до 2 :
2
2 ; 2
4 2
y
1
2
2
1
2
2
4
6
0
2
2
0
31 2
x
2
2
cos
4
2
3
2
2
sin
4
2
10.
Прослідкуємо за координатами точки одиничноготригонометричного кола, яку будемо отримувати в
результаті повороту на різні
додатні кути від 0 до 2 :
2 y
3 1
1 3
3
;
2
2
3
2
2
2
1
2
4
6
0
1
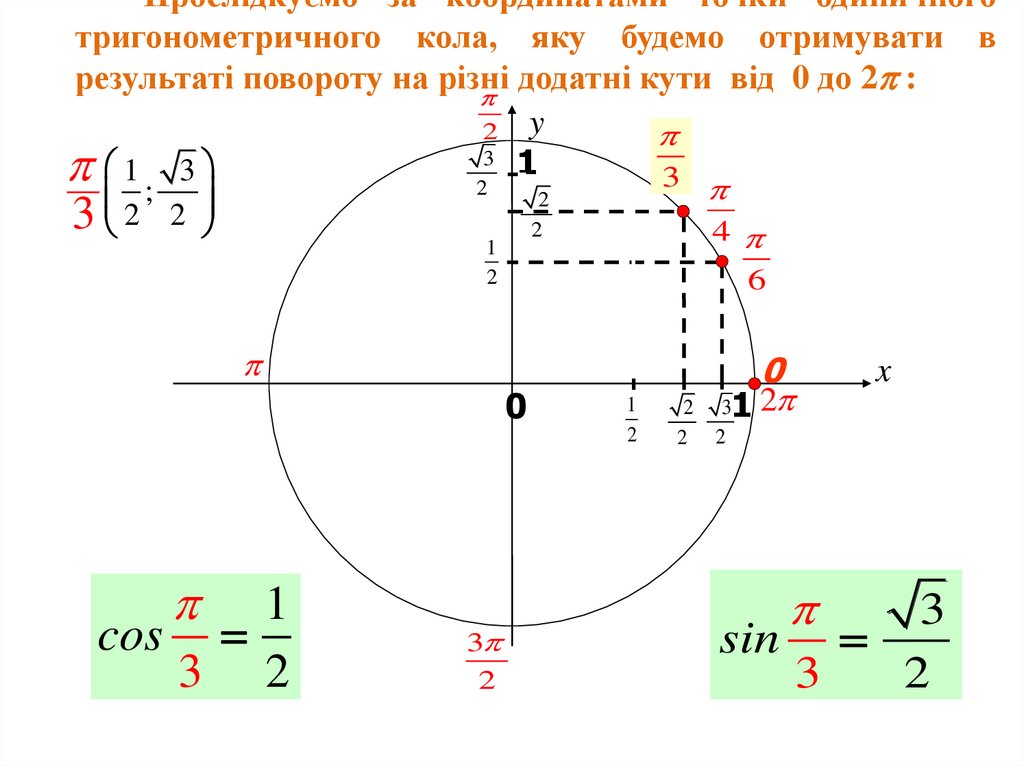
cos
3 2
3
2
1
2
2
2
0
31 2
x
2
3
sin
3
2
11.
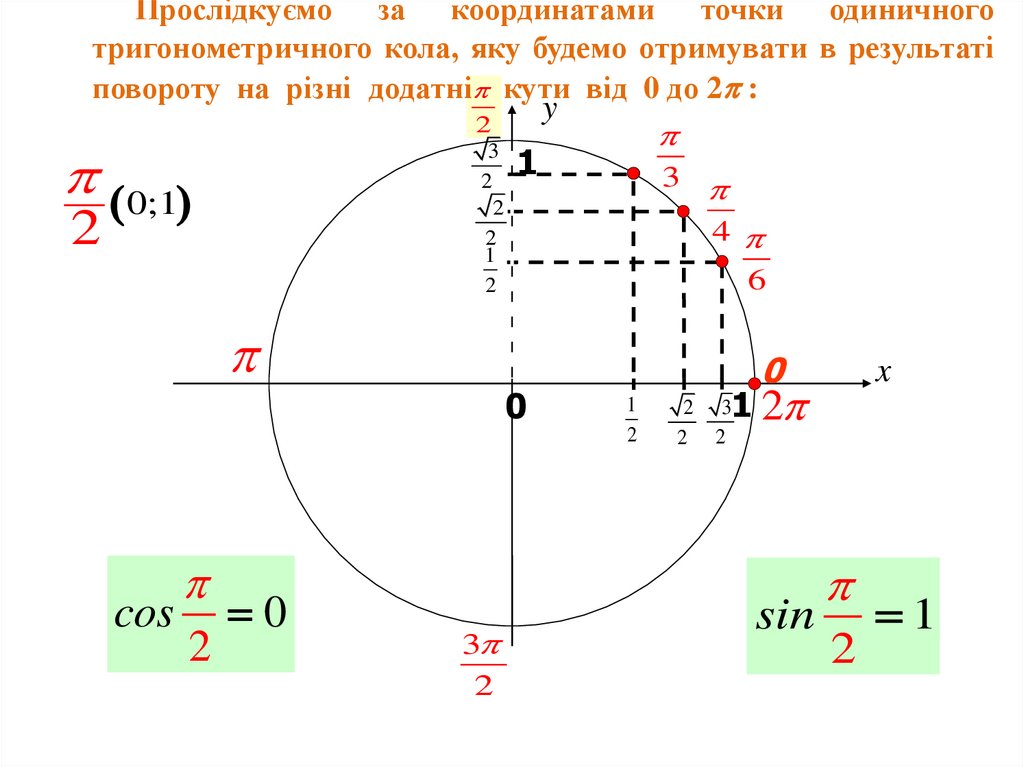
Прослідкуємо за координатами точки одиничноготригонометричного кола, яку будемо отримувати в результаті
повороту на різні додатні кути від 0 до 2 :
y
2
0;1
3
2
2
2
1
2
2
1
3
4
6
0
cos
2
0
3
2
0
1
2
2
2
x
1 2
3
2
sin
2
1
12.
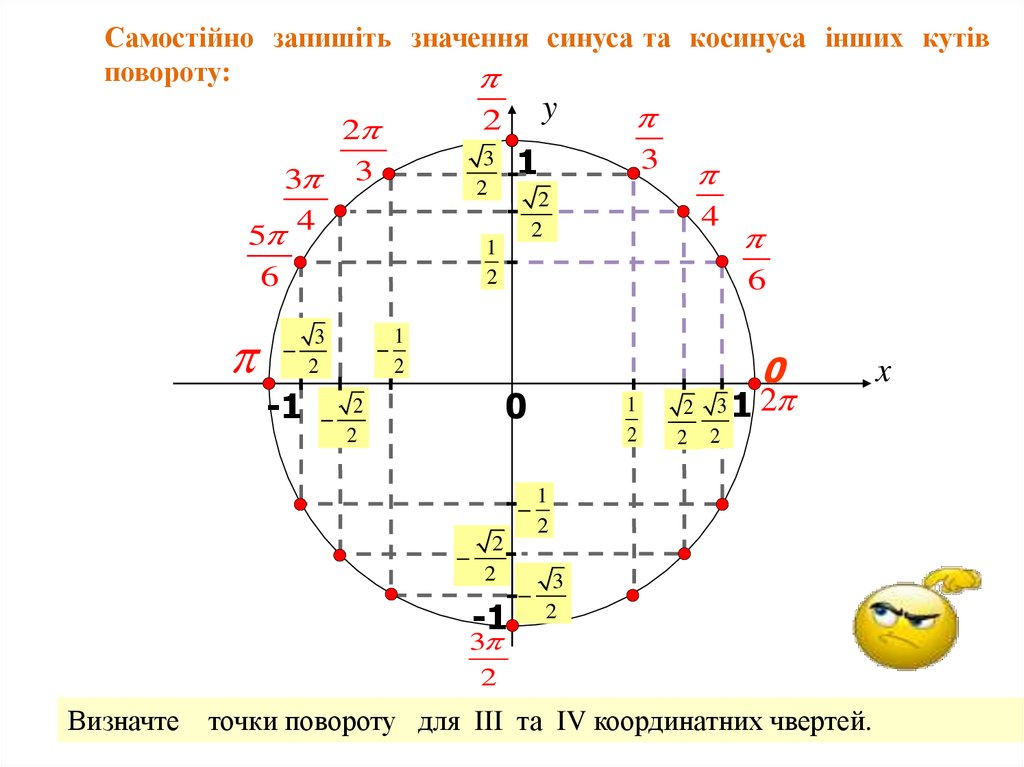
Самостійно запишіть значення синуса та косинуса інших кутівповороту:
2
3 3
4
3
4
0
1
2
2
2
2
-1
3
2
6
1
2
-1 2
2
2
1
2
3
2
1
3
2
5
6
y
2
1
2
3
2
0
2 3 1 2
2
2
Визначте точки повороту для III та IV координатних чвертей.
x
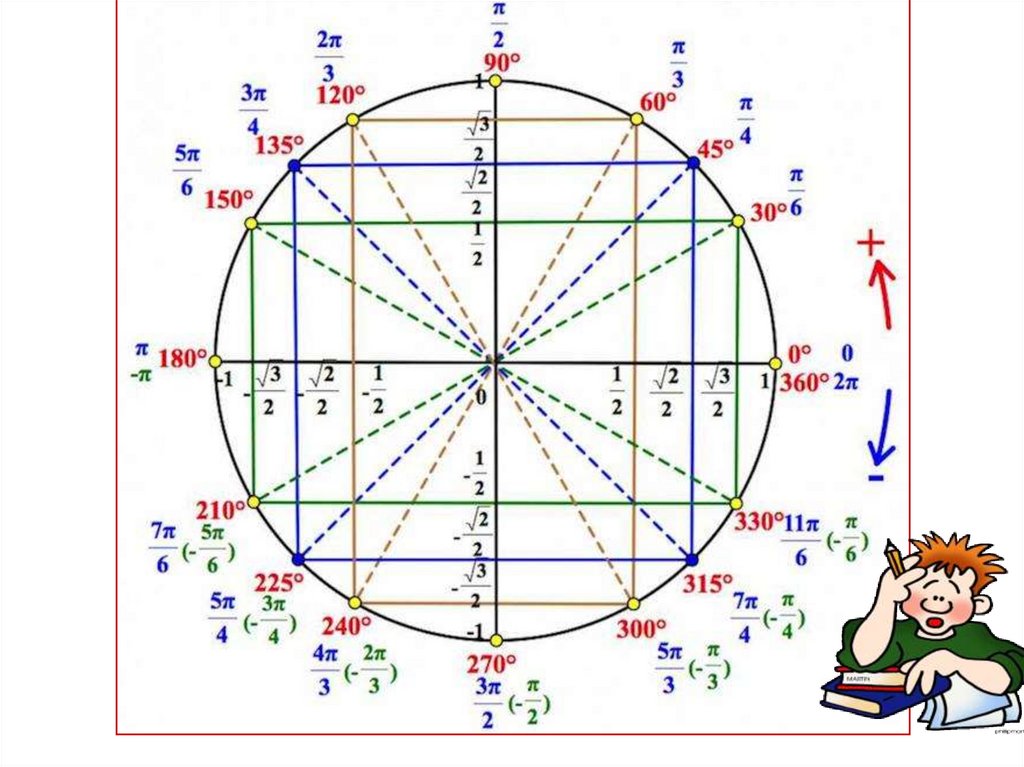
13. Перевірте:
36 2
2 2
4 2
1
2 1 3
3 2
3
4 2
6 2
0
7 3
6 2
5
2
2
4 2
4 1
3
3 2
3
1
2
5 1
3
3 2
7 2
2
4 2
11 3
6 2
0 0
2
1
3
3 2 2
3
2 2 5
14.
15.
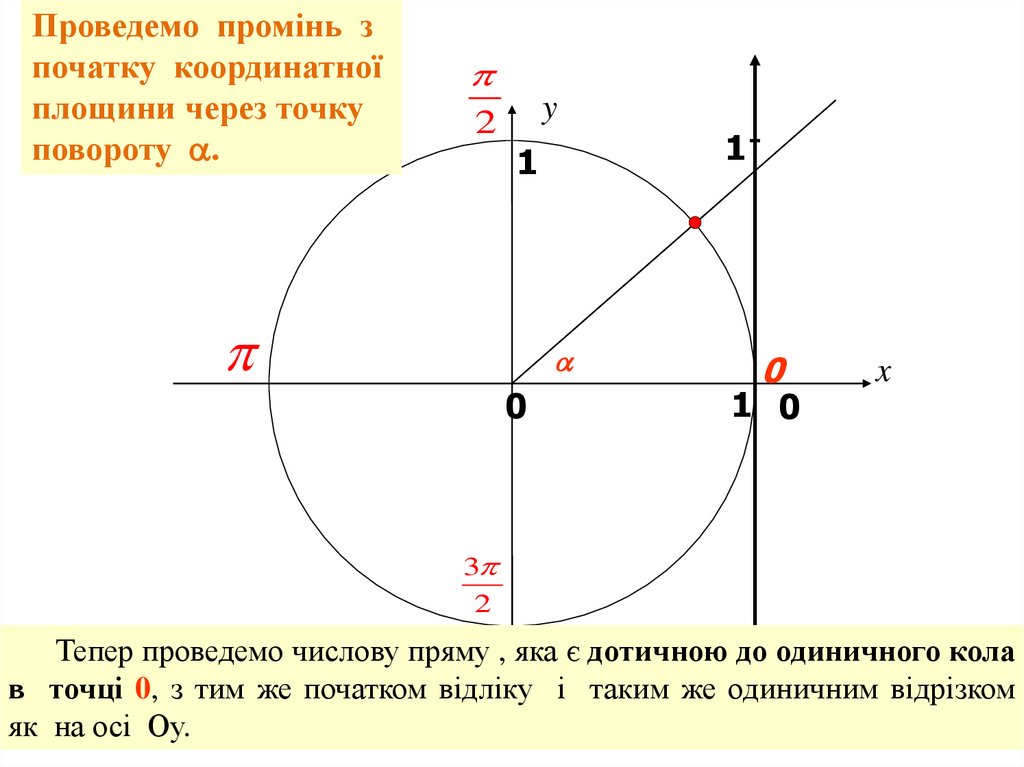
Проведемо промінь зпочатку координатної
площини через точку
повороту .
y
2
1
0
1
0
1 0
x
3
2
Тепер проведемо числову пряму , яка є дотичною до одиничного кола
в точці 0, з тим же початком відліку і таким же одиничним відрізком
як на осі Оу.
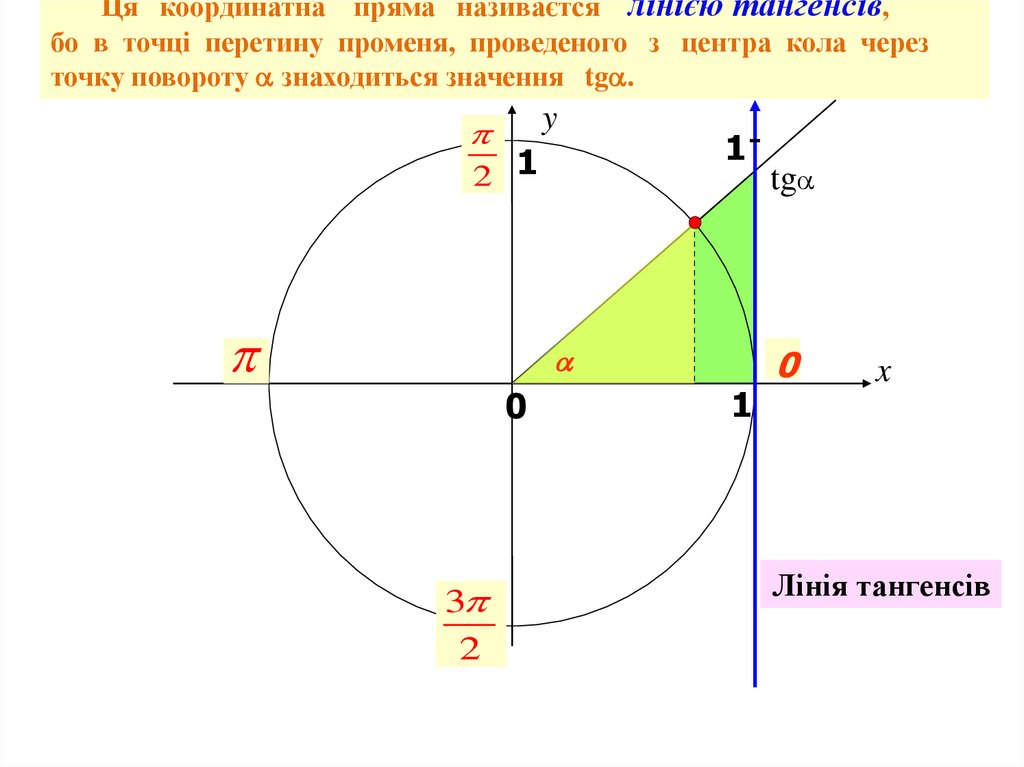
16.
Ця координатна пряма називаєтся лінією тангенсів,бо в точці перетину променя, проведеного з центра кола через
точку повороту знаходиться значення tg .
y
2 1
1
0
3
2
1
tg
0
x
Лінія тангенсів
17.
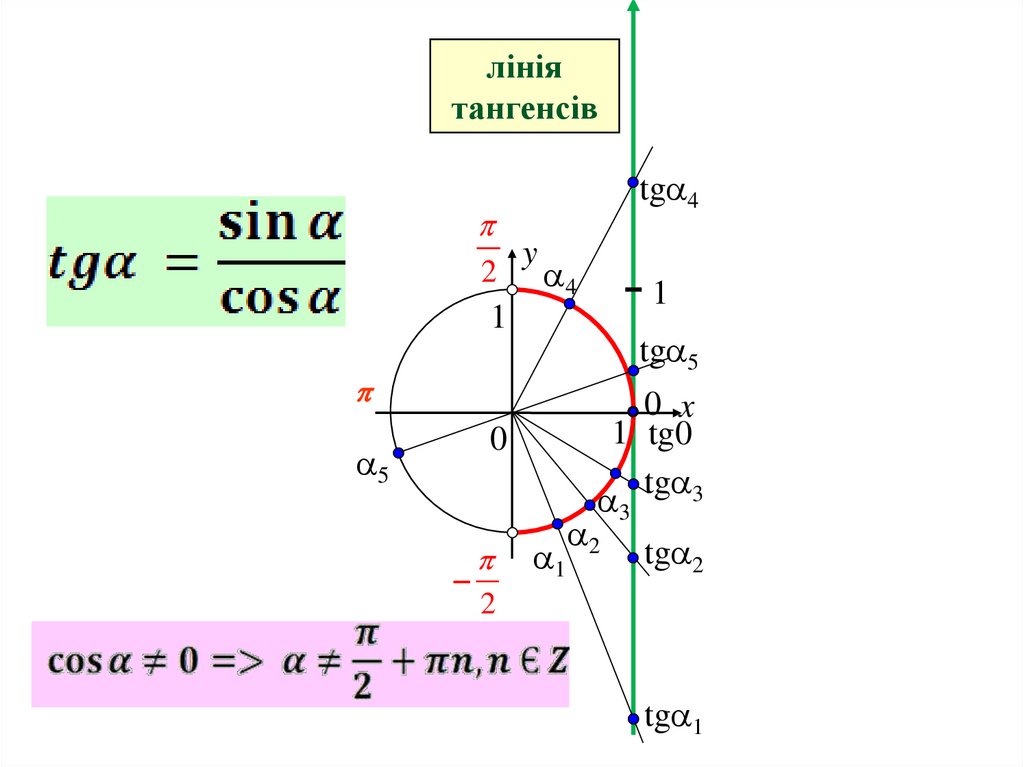
лініятангенсів
tg 4
y
2 4
1
1
tg 5
0 x
1 tg0
tg 3
3
0
5
1
2
tg 2
2
tg 1
18.
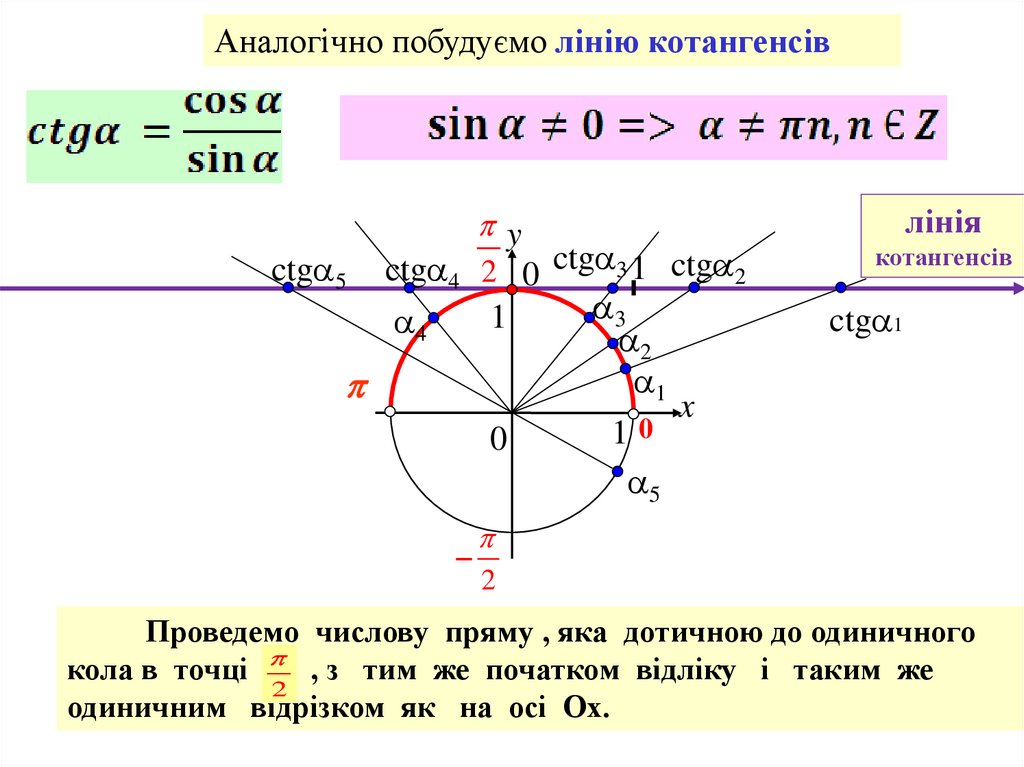
Аналогічно побудуємо лінію котангенсівy
ctg 5 ctg 4 2 0 ctg 3 1 ctg 2
3
1
4
2
1
x
10
0
5
лінія
котангенсів
ctg 1
2
Проведемо числову пряму , яка дотичною до одиничного
кола в точці , з тим же початком відліку і таким же
2
одиничним відрізком як на осі Ох.
19.
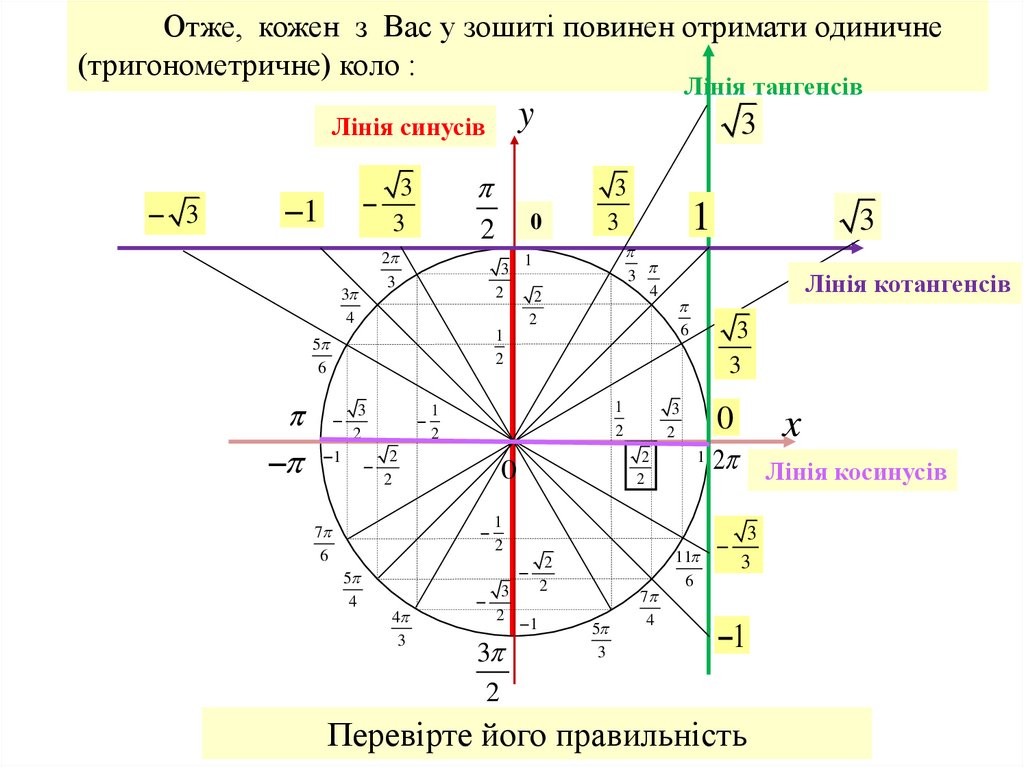
Отже, кожен з Вас у зошиті повинен отримати одиничне(тригонометричне) коло :
y
Лінія синусів
3
1
3
4
3
3
2
2
3
Лінія тангенсів
3
0
3
2
3
3
1
3
4
1
2
2
1
2
5
6
1
23
2
1 22
7
6
1
2
5
4
4
3
3
2
3
2
1
3
3
3
2
1
2
Лінія котангенсів
6
0
2
2
0
3
1
2 Лінія косинусів
3
11
3
2
2
5
3
7
4
x
6
1
Перевірте його правильність
20.
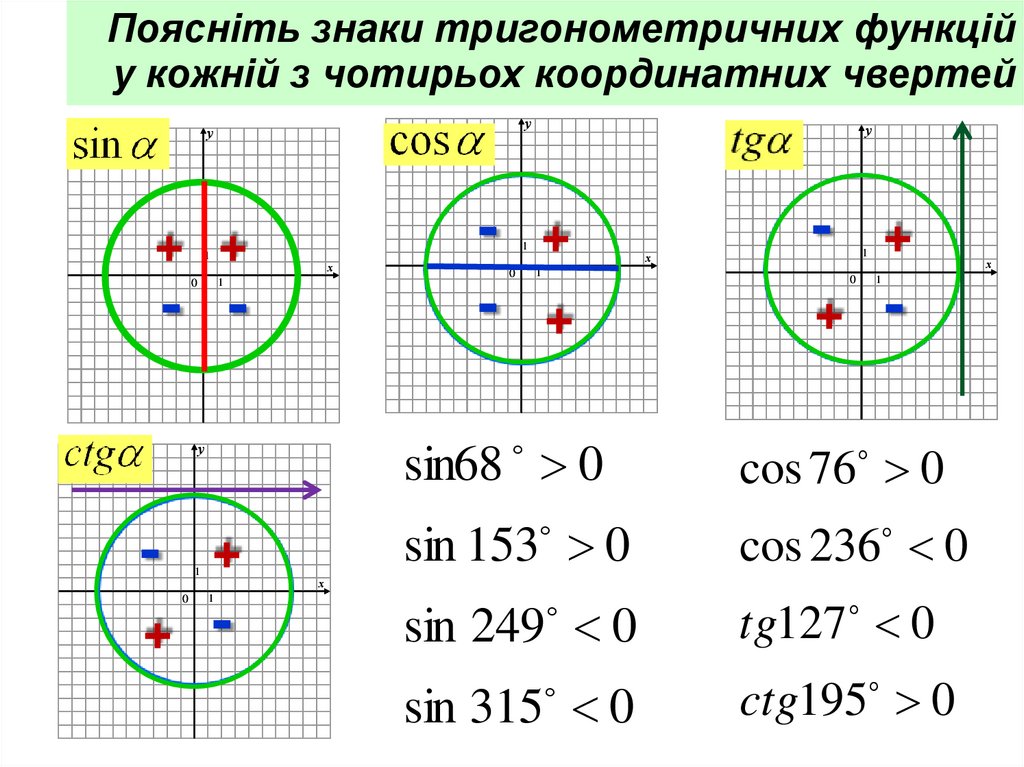
Поясніть знаки тригонометричних функційу кожній з чотирьох координатних чвертей
у
у
+ +
х
1
- -
0
1
- +
+ 1
1
х
- +
+ 1
0
1
sin68 0
cos 76 0
sin 153 0
cos 236 0
sin 249 0
tg127 0
sin 315 0
ctg195 0
у
0
- +
- +
1
1
0
у
х
х
21.
Який знак має вираз :ІІІ чверть
-
ІV чверть +
ІІ чверть
+
ІІІ чверть
+
ІІ чверть
-
І чверть
+
2
ІІ
ІІІ
3
2
y
І
ІV
0
2
22.
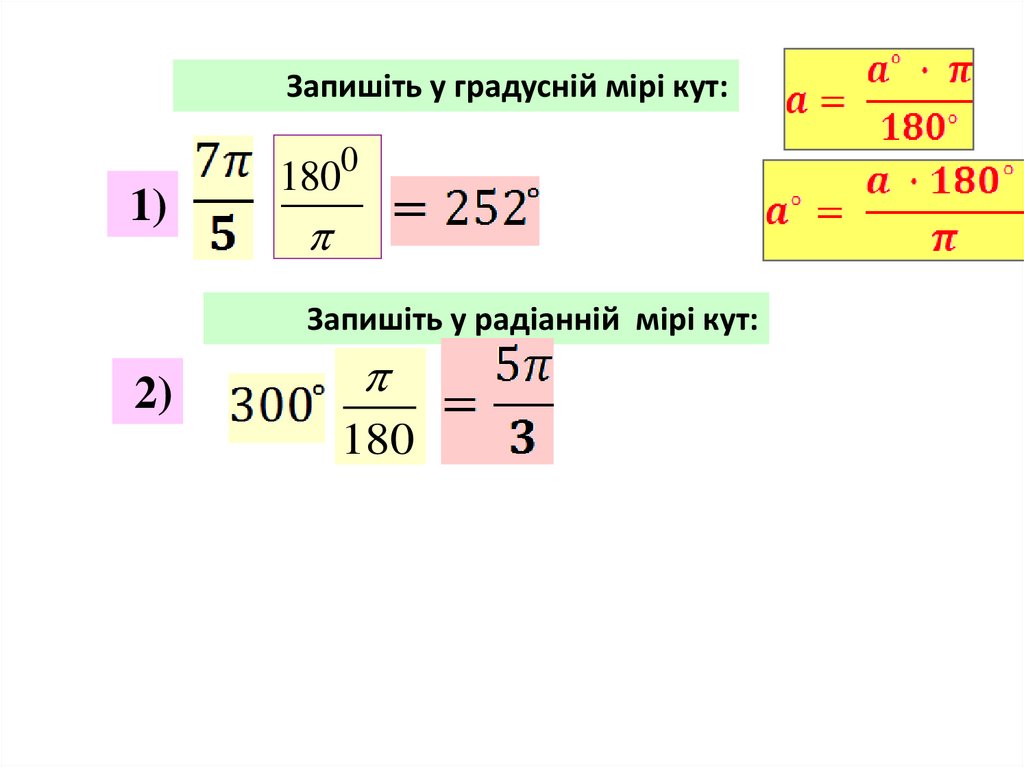
Запишіть у градусній мірі кут:1)
1800
Запишіть у радіанній мірі кут:
2)
180
23.
Який знак має вираз :4)
y
2
0
2 x
-1
5)
Знайдіть значення виразу:
3
2
24.
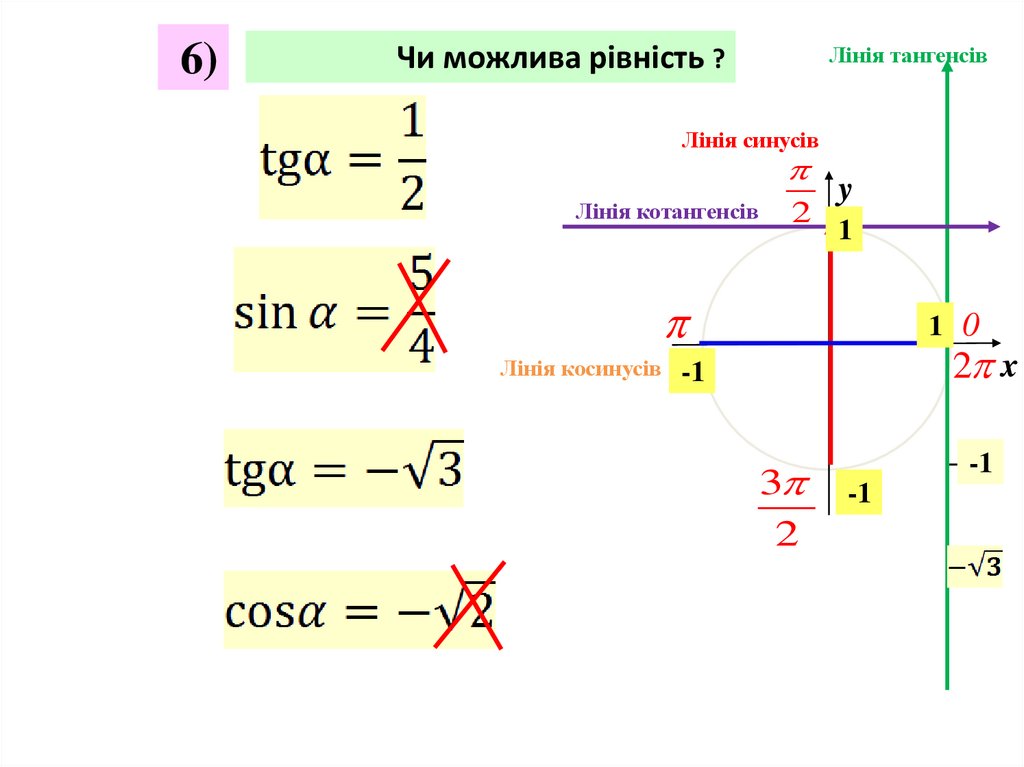
6)Чи можлива рівність ?
Лінія тангенсів
Лінія синусів
Лінія котангенсів
2
y
1
Лінія косинусів
1 0
2 x
-1
3
2
- -1
-1
25. Домашнє завдання
ПідручникМатематика 10 клас
Г.П. Бевз, В.Г. Бевз (2018р)
Сторінка 57 № 227, № 231(б,г)





 Математика
Математика








