Похожие презентации:
Понятие вектора в пространстве
1.
Понятие вектора впространстве
2.
Понятие вектора в пространствеВектор(направленный отрезок) –
отрезок, для которого указано какой из его
концов считается началом, а какой – концом.
В
А
AB
a
M
MM 0
Длина вектора AB – длина отрезка AB.
AB AB
0 0
3.
Коллинеарные векторыДва ненулевых вектора называются коллинеарными,
если они лежат на одной прямой или параллельных
прямых.
Среди коллинеарных различают:
• Сонаправленные векторы
• Противоположно направленные векторы
4.
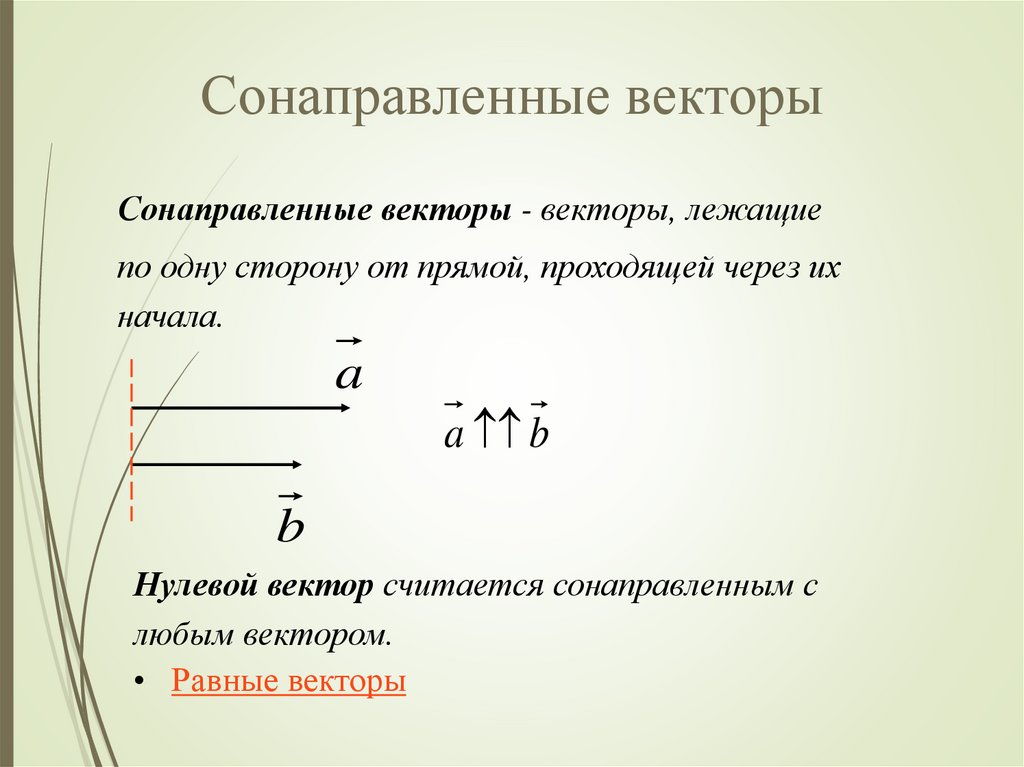
Сонаправленные векторыСонаправленные векторы - векторы, лежащие
по одну сторону от прямой, проходящей через их
начала.
a
a b
b
Нулевой вектор считается сонаправленным с
любым вектором.
• Равные векторы
5.
Равные векторыРавные векторы - сонаправленные векторы,
длины которых равны.
a
a b a b, a b
b
От любой точки можно отложить вектор,
равный данному, и притом только один.
6.
Противоположно направленныевекторы
Противоположно направленные векторы –
векторы, лежащие по разные стороны от прямой,
проходящей через их начала.
a
a b
b
Противоположные векторы
7.
Противоположные векторыПротивоположные векторы – противоположно
направленные векторы, длины которых равны.
a
a b a b, a b
b
Вектором, противоположным нулевому,
считается нулевой вектор.
8.
Признак коллинеарностиЕсли существует такое число k при котором
выполняется равенство a k b и при том
вектор b 0 , то векторы a и b коллинеарн ы.
Доказательство
9.
Доказательство признакаколлинеарности
Два вектора a и b коллинеарн ы тогда и
только тогда, когда имеет место равенство
a kb
вектор k a b, если k 0
( следует из определения
вектор k a b, если k 0
произведения вект ора на число)
Значит вектор b и k a коллинеарн ы,
т.к. сонаправленные и противоложно
направленные векторы лежат на одной
или параллельных прямых.
ч.т.д.








 Математика
Математика








