Наибольшее и наименьшее значение функции

1.

Работу выполнила:
Козачёк Л.П.
учитель математики

2.

Алгоритм решения задач
Этапы
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
критических точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее или
наибольшее
Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3x2 – 27
3
-3
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
x = 3 [0; 4]
x = –3 [0; 4]
3) y(0) = 0
y(4) = 43– 27 4 = – 44
y(3) = 33– 27 3 = –54
В 11
- 5 4
3
10 х
х

3.

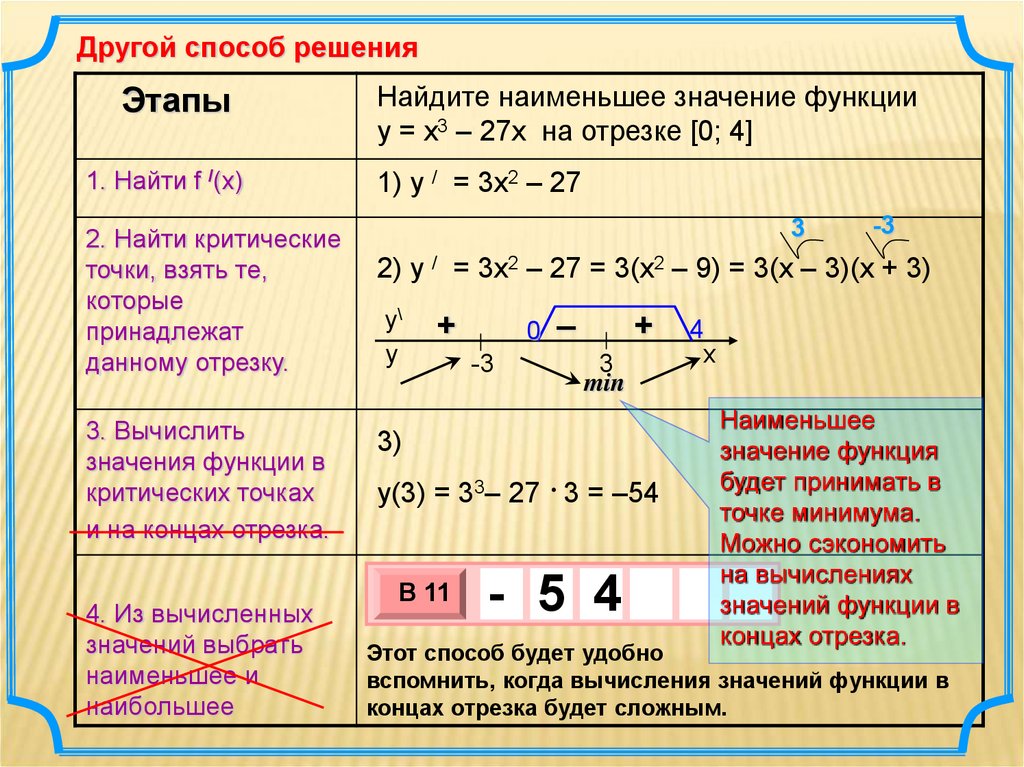
Другой способ решения
Этапы
1. Найти f /(x)
2. Найти критические
точки, взять те,
которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
критических точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее и
наибольшее
Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3x2 – 27
3
-3
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
y\
y
+
0
-3
–
+
3
min
4
x
3)
y(3) = 33– 27 3 = –54
В 11
- 5 4
3
10 х
х
Наименьшее
значение функция
будет принимать в
точке минимума.
Можно сэкономить
на вычислениях
значений функции в
концах отрезка.
Этот способ будет удобно
вспомнить, когда вычисления значений функции в
концах отрезка будет сложным.

4.

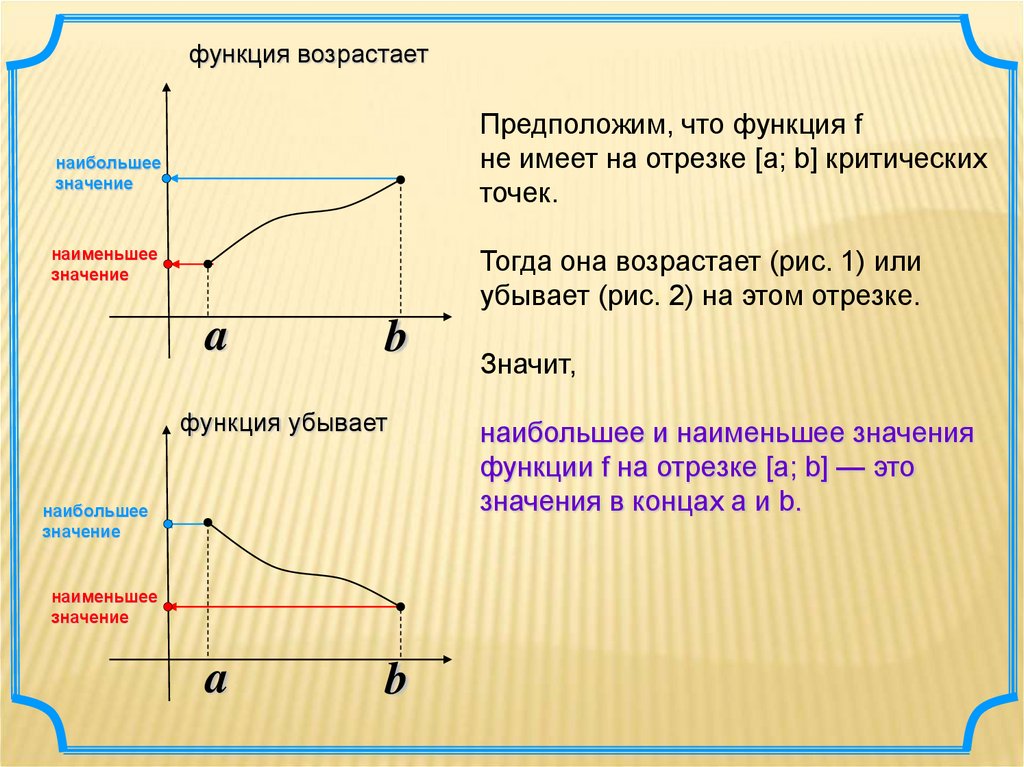
функция возрастает
Предположим, что функция f
не имеет на отрезке [а; b] критических
точек.
наибольшее
значение
наименьшее
значение
Тогда она возрастает (рис. 1) или
убывает (рис. 2) на этом отрезке.
a
b
функция убывает
наибольшее
значение
наименьшее
значение
a
b
Значит,
наибольшее и наименьшее значения
функции f на отрезке [а; b] — это
значения в концах а и b.

5.

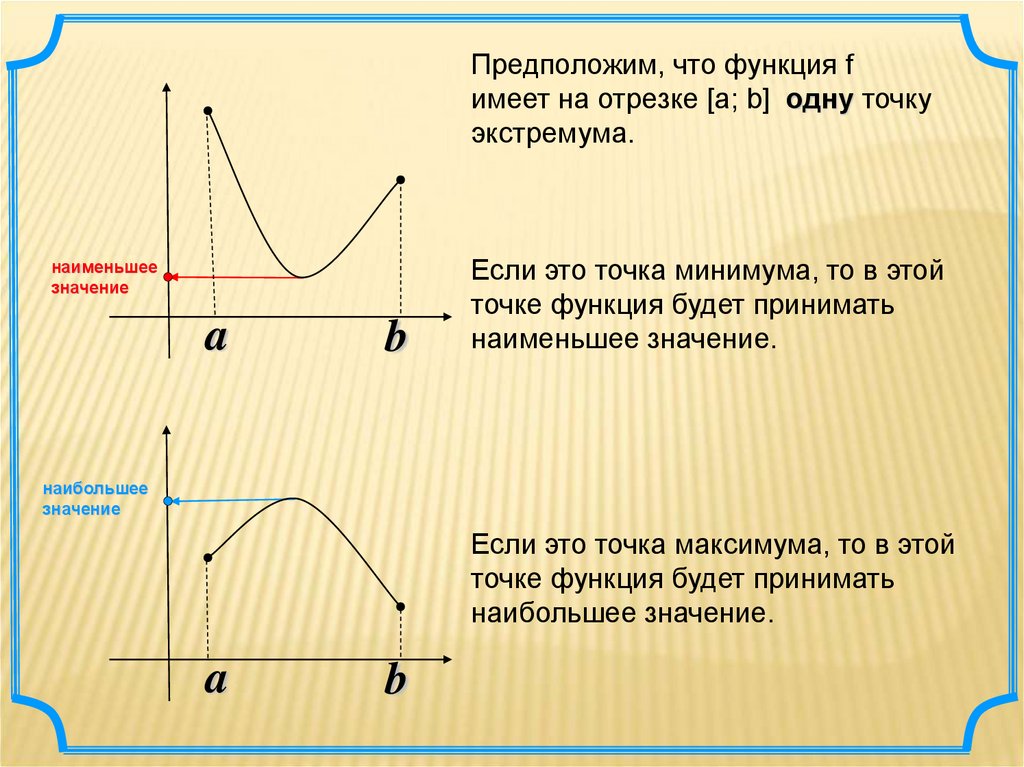
Предположим, что функция f
имеет на отрезке [а; b] одну точку
экстремума.
наименьшее
значение
a
b
Если это точка минимума, то в этой
точке функция будет принимать
наименьшее значение.
наибольшее
значение
Если это точка максимума, то в этой
точке функция будет принимать
наибольшее значение.
a
b

6.

7.

СЛОЖНАЯ ФУНКЦИЯ – функция, представленная как композиция
нескольких функций. Сложная функция – функция от функции.
(
)
Сложная функция u v (x) представлена в виде цепочки простых
функций. v (x) – промежуточный аргумент, x – независимая переменная.
Производная сложной функции равна произведению
производной данной функции по промежуточному
аргументу на производную промежуточного аргумента.
[ u (v (x))] /= u /(v (x ))
v /(x)

8.

Чтобы найти производную сложной функции,
нужно:
1. Определить, какая функция является
внешней и найти по таблице производных
соответствующую производную.
2. Определить промежуточный аргумент.

9.

Функция квадратного корня
у = 5 4х х2
Функция промежуточного аргумента – квадратичная функция
Показательная функция
у=2
х 2 2 х 5
Функция промежуточного аргумента – квадратичная функция
Логарифмическая функция
(
)
у = log 5 4 2 x x 2 3
Функция промежуточного аргумента – квадратичная функция
Степенная функция
у = sin 4 x
Функция промежуточного аргумента – тригонометрическая функция sinx

10.

1. Найдите наименьшее значение функции y = e2x – 6ex + 3 на
отрезке [1; 2]
4– 6e2+ 3
2 – 6e + 3;
y(2)
=
e
1)
y(1)
=
e
Значения функции в
концах отрезка.
– 6ex + 0 = 2ex(ex – 3)
[ u v)] /= u /(v) v / (e2x)/ = e2x (2x)/ = e2x 2 >0
= 2e2x
2) y / =
(
(ex)/
=
ex
(kx)/ = k
0
1) производная
для внешней функции:
x(ex – 3) = 0
2e
(ex)/ = ex x
e –3=0
Наименьшее значение
функция будет принимать в
Найдем критические точки,
точке минимума.
Проверим, принадлежит ли
которые принадлежат Можно сэкономить на
х=ln3 промежутку [1; 2]
заданному отрезку.
вычислениях значений
ln 3отрезка.
2
функции в1концах
(С)/ = 0
ln e ln 3 ln e 2
\
2
y
e 3 e верно
y
e 2,7
Найдем значение
функции в критической
точке.
2 ln 3
у(ln 3) = e
x = ln3 [1; 2]
–
+
ln3
min
6eln3 3 = 9 6 3 3 = 6
x

11.

2. Найдите наибольшее значение функции у =
D(y): 5 – 4х – х2
f /(g (x)) = f /(g (x)) g /(x)
/
( х) =
у =
2 х
Вычислим производную, используя
формулу для вычисления
производной сложной функции.
Найдем критические точки,
которые принадлежат D(у).
1
/
1
=
2 5 4х х2
1
2 5 4х х2
x=–2
(
0
)
5 4х х2 / =
2(2 х )
=( 4 2 х)
2 5 4х х2
D(y)
y\
y
Наибольшее значение
функция примет в точке
максимума.
у ( 2)
5 4х х2
–
+
-2
max
x
= 5 4 ( 2) ( 2) 2 = 5 8 4 = 9 = 3
В 14
3
3
10 х
х

12.

При решении некоторых заданий на вычисление наибольшего и
наименьшего значений функции можно найти ответ и без
вычисления производной.
Сложная функция f (g(x)) представлена в виде цепочки простых
функций.
Где g(x) – промежуточный аргумент, квадратичная функция
g(x) = ax2 +bx + c
Если внешняя функция является монотонно возрастающей на всей области
определения, значит, наибольшее значение она будет иметь, когда функция
промежуточного аргумента, т.е. квадратичная функция будет иметь
наибольшее значение.
А наименьшее значение она будет иметь, когда функция промежуточного
аргумента, т.е. квадратичная функция будет иметь наименьшее значение.
Рассмотрим примеры.

13.

2 способ
2. Найдите наибольшее значение функции у =
Решим задание без вычисления производной.
5 4х х2
D(y): 5 – 4х – х2
0
Функция квадратного корня монотонно возрастает на всей области
определения, значит, наибольшее значение она будет иметь, когда функция
промежуточного аргумента, т.е. квадратичная функция – х2 – 4х + 5 будет
иметь наибольшее значение.
Старший коэффициент квадратного трехчлена равен – 1< 0, значит, ветви
параболы направлены вниз. И наибольшее значение квадратичная функция
будет иметь в вершине.
х0 = b
2a
х0 = -4
D(y)
2*(-1) = -2
Итак, наибольшее значение функция квадратного корня примет, когда
промежуточная квадратичная функция примет наибольшее значение, т.е. в
точке х = – 2. Вычислим его:
у ( 2) = 5 4 ( 2) ( 2) 2 = 5 8 4 = 9 = 3
В 14
3
3
10 х
х

14.

4. Найдите наименьшее значение функции
f /(g (x)) = f /(g (x)) g /(x)
(a )
х
/
= a х ln a
у =2
/
х 2 2 х 5
Вычислим производную, используя
формулу для вычисления
производной сложной функции.
у=2
D(y): x R
(
)
ln 2 x 2 2 x 5 / =
=2
х 2 2 х 5
ln 2 (2 x 2)
x = - 1 D(y)
Найдем критические точки,
которые принадлежат D(у).
–
y\
y
Наименьшее значение
функция примет в точке
минимума.
х 2 2 х 5
+
-1
min
( 1) 2 2 ( 1) 5
у( 1) = 2
В 14
x
= 21 2 5 = 24 = 16
1 6
3
10 х
х

15.

2 способ
4. Найдите наименьшее значение функции
Решим задание без вычисления производной.
х 2 2 х 5
у=2
D(y): x R
Показательная функция с основанием 2>1 монотонно возрастает на всей
области определения. Значит, наименьшее значение она будет иметь, когда
функция промежуточного аргумента, т.е. квадратичная функция х2 + 2х + 5
будет иметь наименьшее значение.
Старший коэффициент квадратного трехчлена равен +1> 0, значит, ветви
параболы направлены вверх. И наименьшее значение квадратичная
функция будет иметь в вершине.
х0 = 2
2* 1
х0 = b
2a
= – 1 D(y)
Итак, наименьшее значение показательная функция примет, когда
промежуточная квадратичная функция примет наименьшее значение, т.е. в
точке х = – 1. Вычислим его:
( 1) 2 2 ( 1) 5
1 2 5
4
у( 1) = 2
=2
В 14
1 6
=2
3
10 х
х
= 16

16.

6. Найдите наибольшее значение функции
(
)
у = log 5 4 2 x x 2 3
Решим задание без
вычисления производной.
D(y): 4 – 2х – х2
>0
Логарифмическая функция с основанием 5 является монотонно
возрастающей на всей области определения. Значит, наибольшее значение
она будет иметь, когда функция промежуточного аргумента, т.е.
квадратичная функция 4 – 2х – х2 будет иметь наибольшее значение.
Старший коэффициент квадратного трехчлена равен –1<0, значит, ветви
параболы направлены вниз. И наибольшее значение квадратичная функция
будет иметь в вершине.
х0 = -2 = -1
2(-1)
х0 = b
2a
(
1
)
у( 1) = log 5 4 2 ( 1) ( 1) 3 = log 5 (4 2 1) 3 = log 5 5 3
2
=4
В 14
4
3
10 х
х