Нахождение наибольшего и наименьшего значений функции на отрезке с помощью производной

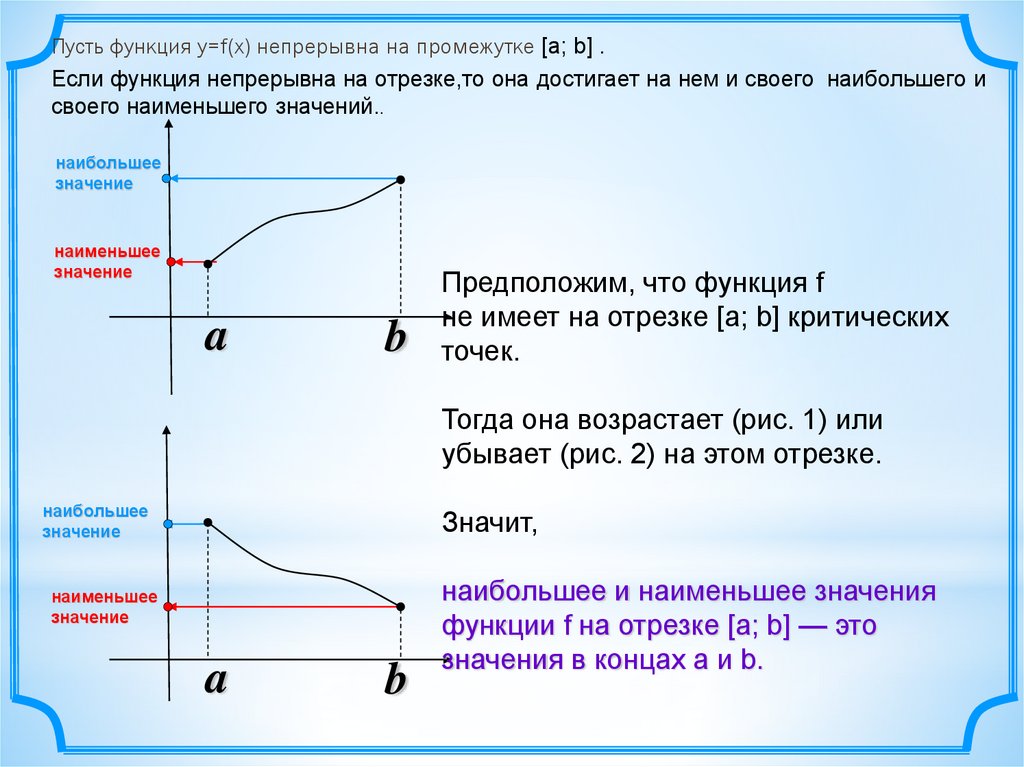
Пусть функция у=f(х) непрерывна на промежутке [а; b] .
Если функция непрерывна на отрезке,то она достигает на нем и своего наибольшего и
своего наименьшего значений..
наибольшее
значение
наименьшее
значение
a
b
Предположим, что функция f
не имеет на отрезке [а; b] критических
точек.
Тогда она возрастает (рис. 1) или
убывает (рис. 2) на этом отрезке.
наибольшее
значение
Значит,
наименьшее
значение
a
b
наибольшее и наименьшее значения
функции f на отрезке [а; b] — это
значения в концах а и b.

3.

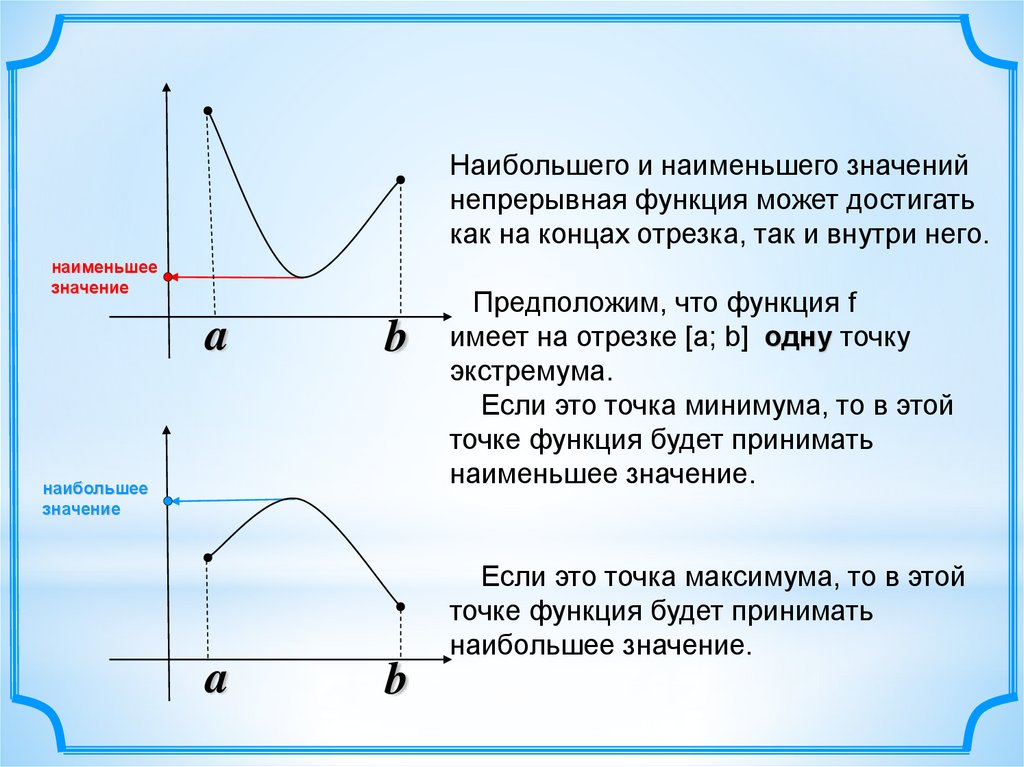
Наибольшего и наименьшего значений
непрерывная функция может достигать
как на концах отрезка, так и внутри него.
наименьшее
значение
a
b
наибольшее
значение
Предположим, что функция f
имеет на отрезке [а; b] одну точку
экстремума.
Если это точка минимума, то в этой
точке функция будет принимать
наименьшее значение.
Если это точка максимума, то в этой
точке функция будет принимать
наибольшее значение.
a
b

4.

5.

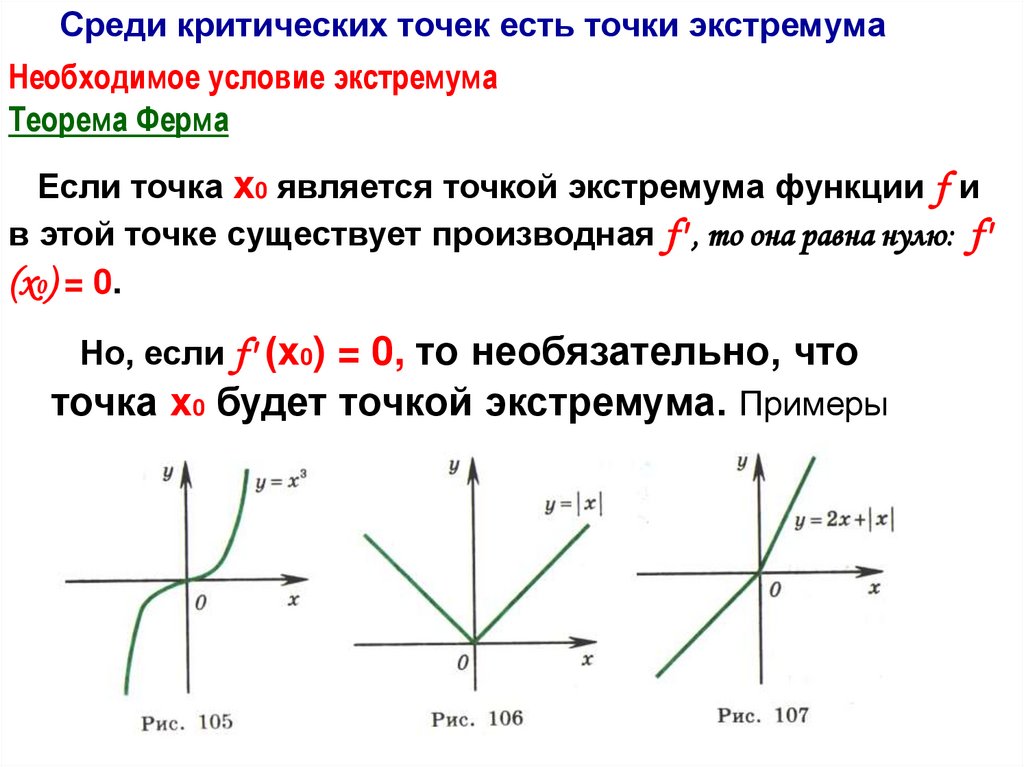
Среди критических точек есть точки экстремума
Необходимое условие экстремума
Теорема Ферма
Если точка х0 является точкой экстремума функции f и
в этой точке существует производная f' , то она равна нулю: f'
(х0) = 0.
Но, если f' (х0) = 0, то необязательно, что
точка х0 будет точкой экстремума. Примеры

6.

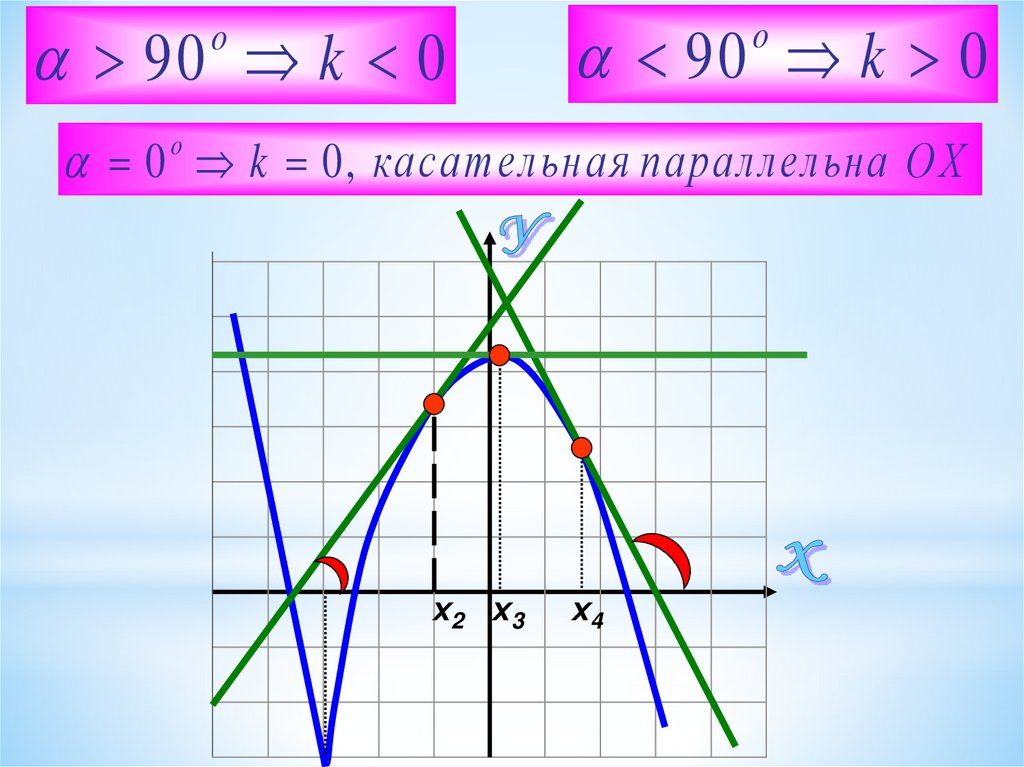
90 k 0
o
90 k 0
o
0 k 0 , касательна я параллельн а ОХ
o
х2 х3
х4

7.

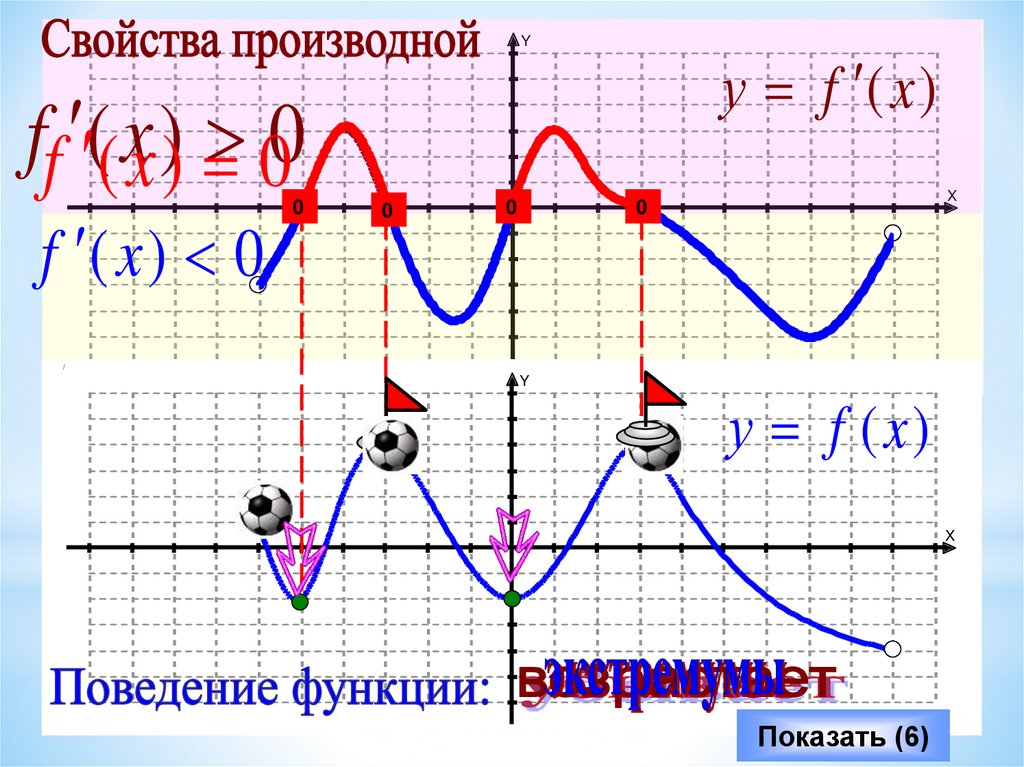
Y
ff ((xx )) 00
f ( x ) 0
0
0
0
у f ( x )
X
0
Y
у f ( x)
X
Показать (6)

8.

9.

Алгоритм решения задач
Этапы
1. Найти f /(x)
2. Найти
стационарные
точки, взять те,
которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
стационарных
точках и на концах
отрезка.
4. Из вычисленных
значений выбрать
наименьшее или
наибольшее
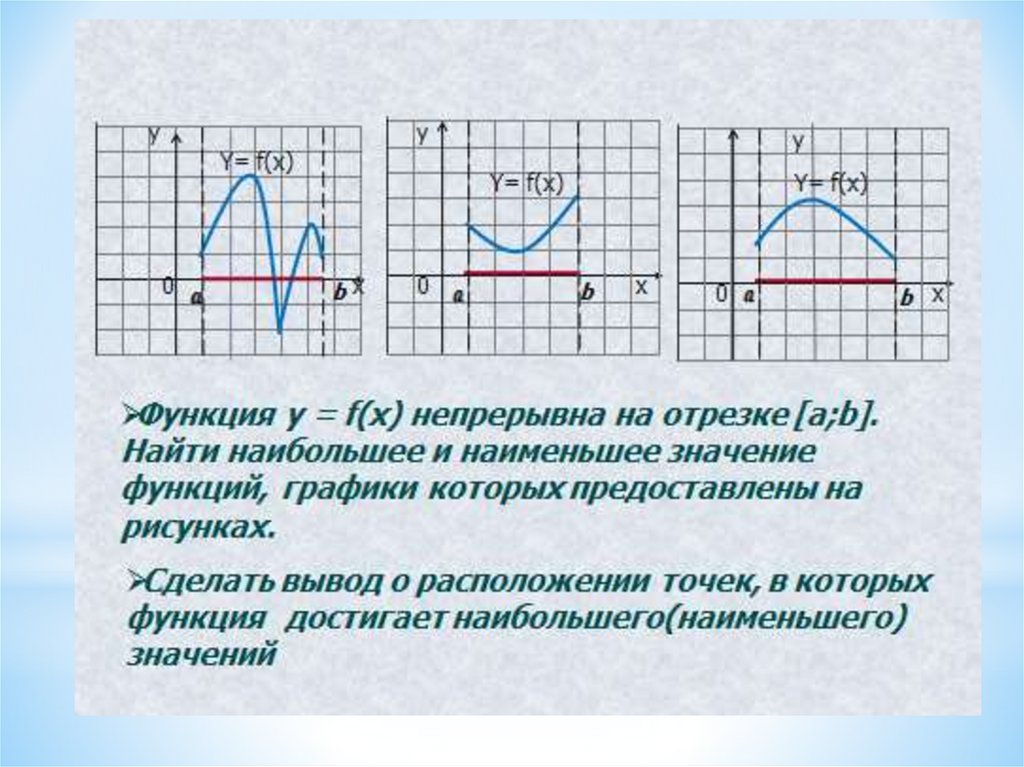
Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3x2 – 27
3
-3
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
x = 3 [0; 4]
x = –3 [0; 4]
3) y(0) = 0
y(4) = 43– 27 4 = – 44
y(3) = 33– 27 3 = –54
- 5 4
3
10 х
х

10.

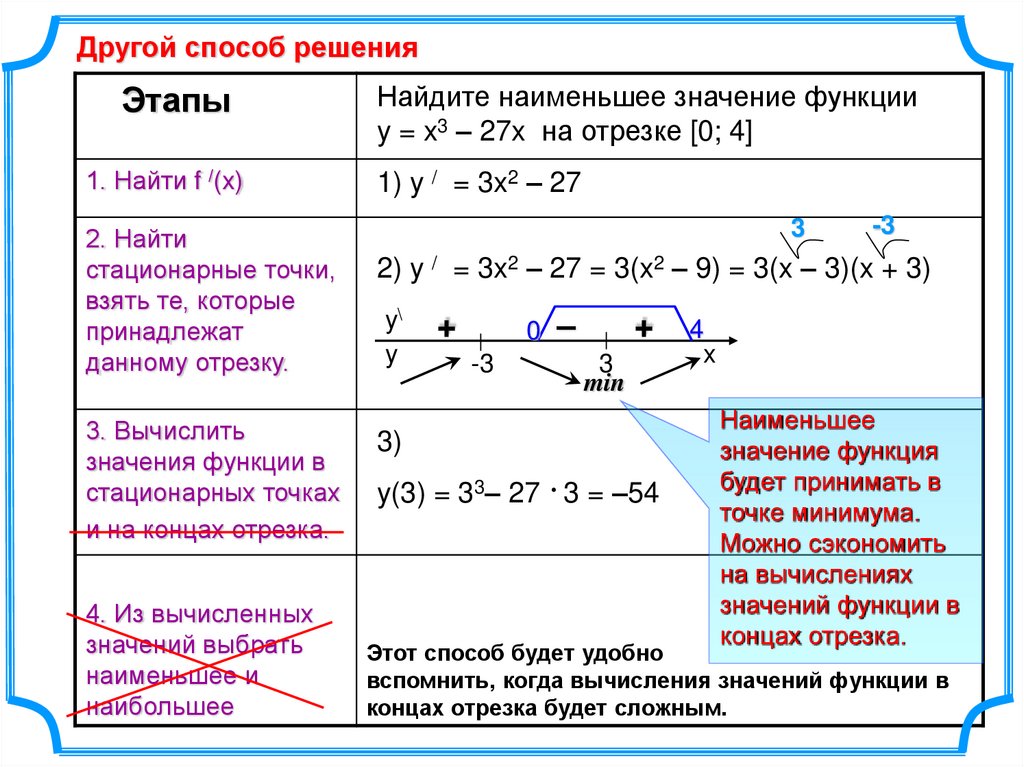
Другой способ решения
Этапы
1. Найти f /(x)
2. Найти
стационарные точки,
взять те, которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
стационарных точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее и
наибольшее
Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3x2 – 27
3
-3
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
y\
y
+
0
-3
–
+
3
min
3)
y(3) = 33– 27 3 = –54
4
x
Наименьшее
значение функция
будет принимать в
точке минимума.
Можно сэкономить
на вычислениях
значений функции в
концах отрезка.
Этот способ будет удобно
вспомнить, когда вычисления значений функции в
концах отрезка будет сложным.

11.

2. Найдите наибольшее значение функции у
D(y): 5 – 4х – х2
f /(g (x)) f /(g (x)) × g /(x)
/
( х)
у
2 х
Вычислим производную, используя
формулу для вычисления
производной сложной функции.
Найдем критические точки,
которые принадлежат D(у).
2 5 4х х2
1
2 5 4х х2
x=–2
y\
y
Наибольшее значение
функция примет в точке
максимума.
у ( 2)
1
/
1
5 4х х2
(
0
)
5 4х х2 /
2(2 х )
( 4 2 х)
2 5 4х х2
D(y)
+
–
-2
max
x
5 4 ( 2) ( 2) 2 5 8 4 9 3

12.

Найдите наибольшее значение функции
Решим задание без вычисления производной
Функция наименьшее значение будет иметь тогда , когда функция
промежуточного аргумента, т.е. квадратичная функция -х2 - 4х + 5 будет
иметь наименьшее значение.
Старший коэффициент квадратного трехчлена равен -1 меньше 0, значит,
ветви параболы направлены вниз. И наибольшее значение квадратичная
функция будет иметь в вершине.
х0 b
2a
Х=4/(-2)=-2

13.

Найти наибольшее и наименьшее значение функции y= x2 - 3x + 5 + |1-x| на
отрезке [0;4].
Решение: Раскроем модуль и преобразуем нашу функцию:
y= x2 - 3x + 5 + 1 - x, при x ≤ 1.
y= x2 - 3x + 5 - 1 + x, при x ≥ 1.
Тогда наша функция примет вид:
f(x)={ x2−4x+6,приx≤1
x2−2x+4,приx≥1
f(x)={ x2−4x+6,приx≤1
x2−2x+4,приx≥1
Найдем критические точки:
Найдем наибольшее и наименьшее значения функции, для этого вычислим
значения функции в стационарных точках и на концах отрезка:
Ответ: Функция достигает наименьшего значения в стационарной точке x= 1,
yнаим.= 3. Функция достигает наибольшего значения на конце отрезка в точке
x= 4, yнаиб.= 12.

14.

7.
/
1
1
÷
2
х
х
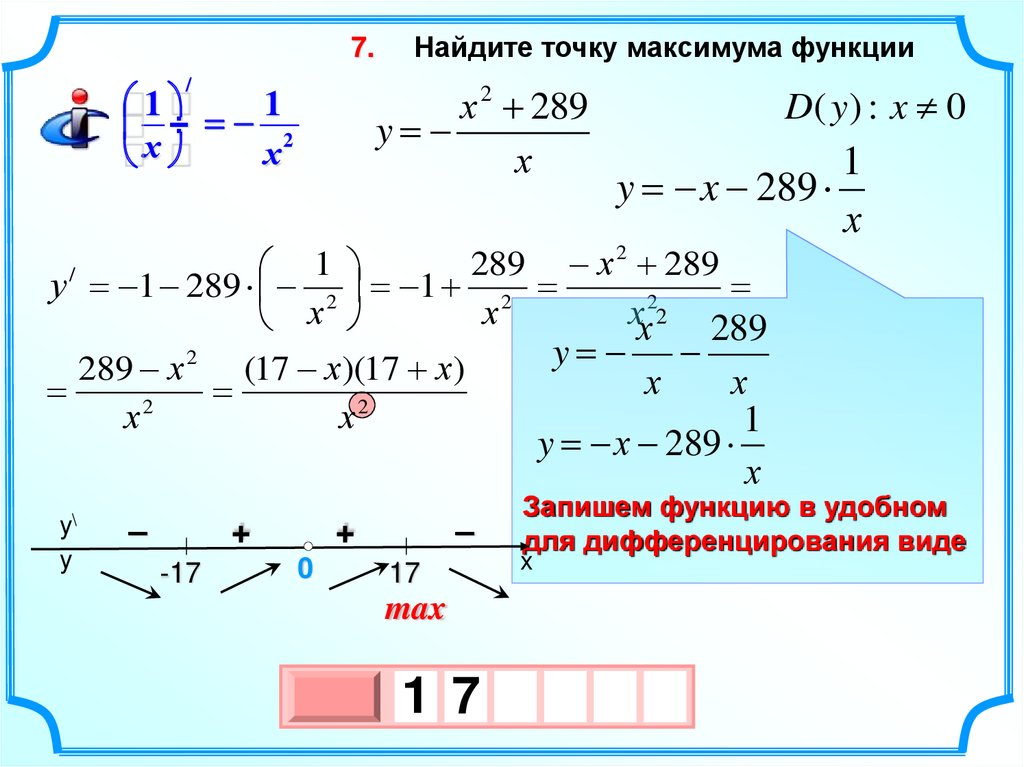
Найдите точку максимума функции
х 2 289
y
х
D( y ) : x 0
1
y x 289
х
2
1
289
х
289
/
у 1 289 2 1 2
2
х
хх 2 289
х
y
289 х 2 (17 х )(17 х )
х
х
2
2
х
х
1
y х 289
y\
y
–
+
-17
–
+
0
17
Запишем функцию в удобном
для дифференцирования виде
x
max
1 7
х
3
10 х
х

15.

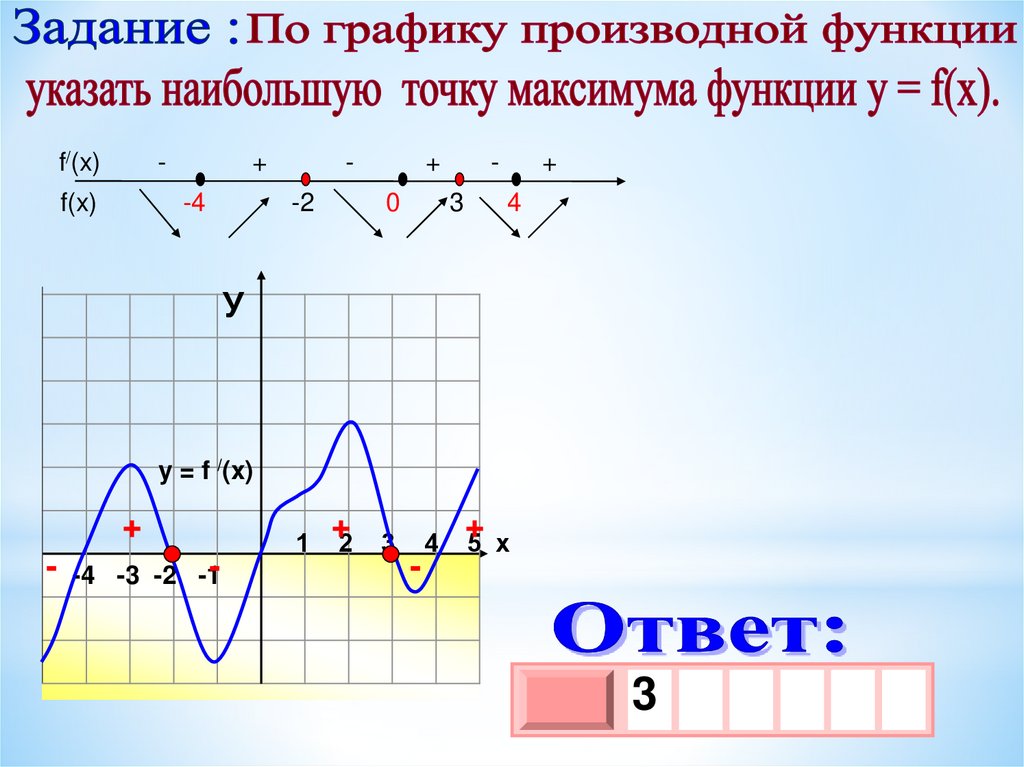
f/(x)
-
f(x)
+
-4
-2
+
0
3
+
4
У
y = f /(x)
+
-
-4 -3 -2 -1-
1
+2
3
-
4
+
5
х
3
3
10 х
х

16.

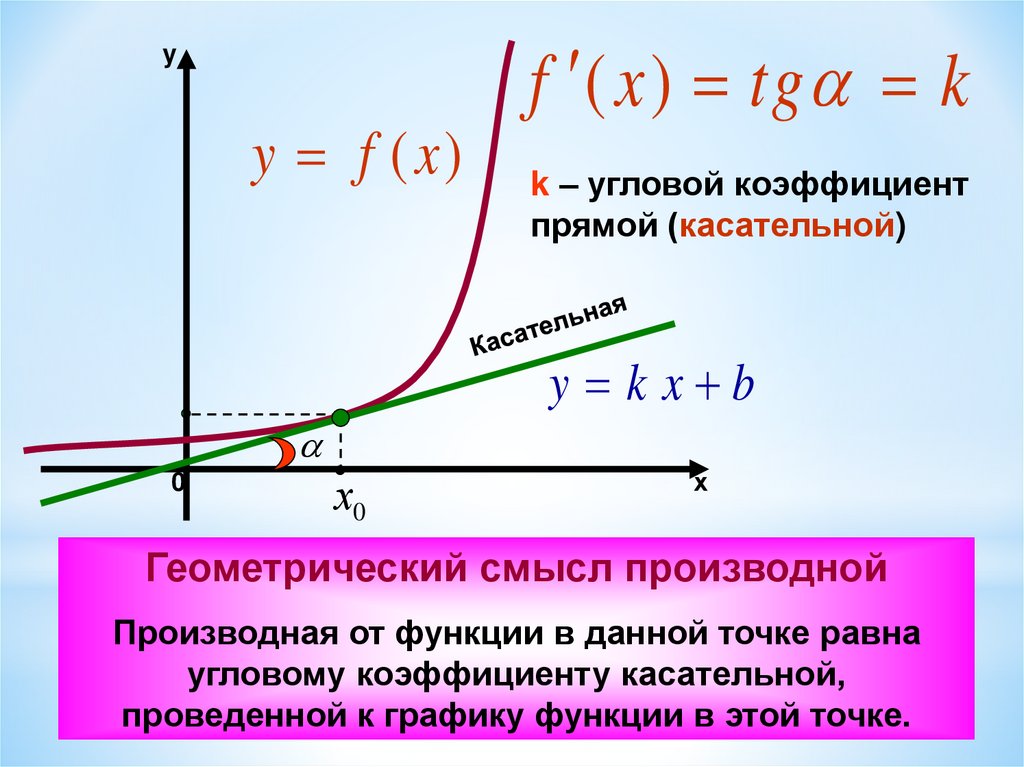
y
y f ( x)
f ( x ) tg k
k – угловой коэффициент
прямой (касательной)
y k x b
0
х0
х
Геометрический смысл производной
Производная от функции в данной точке равна
угловому коэффициенту касательной,
проведенной к графику функции в этой точке.

17. Написать конспект и задачи, выполняя чертежи. Высылать в личном сообщении в вк или на почту [email protected] Перед

НАПИСАТЬ КОНСПЕКТ И ЗАДАЧИ,
ВЫПОЛНЯЯ ЧЕРТЕЖИ.
ВЫСЫЛАТЬ В ЛИЧНОМ
СООБЩЕНИИ В ВК ИЛИ НА ПОЧТУ
[email protected]
ПЕРЕД КАЖДЫМ ЗАДАНИЕМ В
ТЕТРАДИ ПИШЕМ ФИО, ДАТА, ТЕМА
УРОКА

English Русский Правила