Поперечная волна. Практическое занятие №1

1.

ФИЗИКА
2-й курс, 4-й семестр
Практическое занятие №1
Авторы курса: Гринкруг Мирон Соломонович,
Ткачёва Юлия Ильинична,
Новгородов Никита Александрович

2.

ЗАДАЧА №1
Разность
хода двух интерферирующих
волн монохроматического
равнадлины
четверти
длины
волны. Определите
градусахфаз
разность фаз
Разность хода
двух интерферирующих
волн монохроматического
света равнасвета
четверти
волны.
Определите
в градусах вразность
Разность
хода
двух
интерферирующих
волн
монохроматического
света
равна
четверти
длины
волны.
Определите
в
градусах
разность
фаз
Разность
хода
двух
интерферирующих
волн
монохроматического
света
равна
четверти
длины
волны.
Определите
в
градусах
разность
фаз
колебаний.
колебаний.
колебаний.
колебаний.
Дано: Для
Решение.
Для получения
интерференционной
картины
волны
должны
быть когерентными,
т.е. иметь
одну
Дано:
Решение.
получения
устойчивойустойчивой
интерференционной
картины волны
должны
быть
когерентными,
т.е. иметь одну
частоту
и частоту и
Дано:
Решение.
Для
получения
устойчивой
интерференционной
картины
волны
должны
быть
когерентными,
т.е.
иметь
одну
частоту
Дано:
Решение.
должны быть 2
когерентными,
т.е. иметь одну частотуии
Для получения устойчивой интерференционной картины волны
x
2
x
х волны
длину
волны
(в точке наложения).
бегущей
.
х длину
y волны:
y sin y
t y02sin
(в точке
наложения).
Уравнение Уравнение
бегущей волны:
2 x x t.
хх 4 длину
sin t t . .
длину4волны
волны(в(вточке
точкеналожения).
наложения).Уравнение
Уравнениебегущей
бегущейволны:
волны: yy yy000sin
?φ – ?
?φ – 4?4
?φ
?φ––? ?
2 x 2 x2 x 2 2 x 2 0 900 .
из волн
Фаза
каждой
Фаза каждой
из волн
xx 22 90 0.0
t 22 x x t. 22 .
90
Фаза
90 . . 2
Фазакаждой
каждойизизволн
волн t t . . 4 2 4
0
4
2
4
2
Ответ: ?φОтвет:
= 9000.0 ?φ = 90 .
Ответ:
Ответ:?φ
?φ==90
90. .
© Гринкруг М.С., Ткачева Ю.И., Новгородов Н.А., 2022

3.

ЗАДАЧА №2
Поперечная волна распространяется вдоль упругого шнура со скоростью 15 м/с. Период колебаний точек шнура 1,2 с, амплиту
колебаний А = 2 см. Определите длину волны, фазу и смещение точки, отстоящей на расстоянии 45 м от источника колебаний, через 4 с.
Поперечная
волна
распространяется
вдоль
упругого
шнура
сососкоростью
Поперечная
скоростью
1515м/с.
м/с.
Период
колебаний
точек
шнура
1,2
с,с,амплитуда
амплитуда
Поперечнаяволна
волнараспространяется
распространяетсявдоль
вдольупругого
упругогошнура
шнурасо
скоростью15
м/с.Период
Периодколебаний
колебанийточек
точекшнура
шнура1,2
1,2с,
амплитуда
колебаний
А
=
2
см.
Определите
длину
волны,
фазу
и
смещение
точки,
отстоящей
на
расстоянии
45
м
от
источника
колебаний,
через
с.
колебаний
А
=
2
см.
Определите
длину
волны,
фазу
и
смещение
точки,
отстоящей
на
расстоянии
45
м
от
источника
колебаний,
через
с.с.
λ = υ•Т = 15•1,2
= 18 м. Из
волныколебаний,
находим фазу
и44 4
смещение:
Дано: длину волны, фазу
Решение.
Длина
волны
колебаний А = 2 см. Определите
и смещение
точки,
отстоящей
на расстоянии
45уравнения
м от источника
через
–2
А = 2 см = 2•10 м;
18 м.xИз
уравнения волны находим фазу и смещение:
Дано:
Решение.
Длина
волны
= =υ•Т
υ•Т
15•1,2
yυ•Т
==A=15•1,2
15•1,2
sin == =18
t 18
м.м.Из
, уравнения
фаза
колебаний
рассматриваемой
точки:
Дано:
Решение.
Длина
волны
находим
Из
υ = 15 м/с;
Дано:
Решение.
Длинаволны
волныλλ λ=
уравнения
волны
находимфазу
фазуи исмещение:
смещение:
–2
–2–2
А
=
2
см
=
2•10
м;
x x
АА= =2 2смсм= =2•10
Т = 1,2 с; x
2•10 м;м;
= A
A45A sin
sin
tt
фаза
колебаний
рассматриваемой
точки:
,, ,фаза
==15
1515м/с;
м/с;
yyхy
υυ υ=
sin
t
фазаколебаний
колебаний
рассматриваемой
м;
м/с;
xрассматриваемой
2
x точки:
2точки:
45
Т
=
1,2
с;
t
t
4 5,23 рад. Смешение этой точки через 4 с: у = А•sinφ ? –1,73•10–2 м.
Т Т==1,2
t=4c
1,2с;с;
15
= =45
4545м;
м;м;
x x 22
2 xx x 22
2 45
4545 T 1,2
хх х=
–2
λ –
? t x
–2–2
t
4
5
,
23
рад.
Смешение
этой
точки
через
44 4с:
уу у=
А•sinφ
?? ?–1,73•10
м.
tt =
=t =44 4cc c
t
t
4
5
,
23
рад.
Смешение
этой
точки
через
с:
=
А•sinφ
–1,73•10
м.м.
t
t
4
5
,
23
рад.
Смешение
этой
точки
через
с:
=
А•sinφ
–1,73•10
φ – ?
T
1
,
2
15
T
1
,
2
15
T
1
,
2
15
λλ λ–– –?? ?
y–?
φ
–
?
φ φ– –? ?
yy y–– –?? ?
Ответ: λ = 18 м, φ = 5,23 рад, y = –1,73•10–2 м.
–2
–2 м.
Ответ:
= =18
1818м,
м,м,φ
φ φ=
= =5,23
5,23
рад,
= =–1,73•10
–1,73•10
Ответ:
Ответ:λλ λ=
5,23рад,
рад,yy y=
–1,73•10–2м.
м.
© Гринкруг М.С., Ткачева Ю.И., Новгородов Н.А., 2022

4.

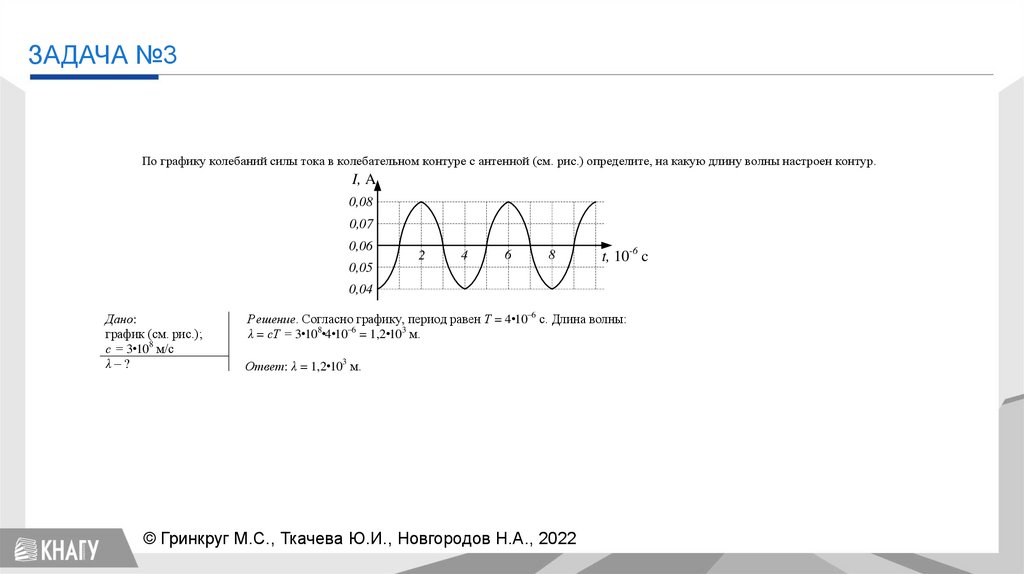
ЗАДАЧА №3
По графику колебаний силы тока в колебательном контуре с антенной (см. рис.) определите, на какую длину волны настроен контур.
I, A
0,08
0,07
0,06
2
4
6
8
0,05
Дано:
Дано:
график
(см.
рис.);
график
(см.
рис.);
8 8
с =с 3•10
м/см/с
= 3•10
λ –λ?– ?
t, 10-6 c
0,04 Решение. Согласно графику, период равен Т = 4•10–6 с. Длина волны:
Дано:
график (см. рис.);
λ = сТ = 3•108•4•10–6 = 1,2•103 м.
–6 –6
8 Согласно
Решение.
графику,
период
равен
Т =Т4•10
с. Длина
волны:
графику,
период
равен
= 4•10
с. Длина
волны:
сРешение.
= 3•10Согласно
м/с
8 8 –6 –6
3 3
λ =λλсТ
=
3•10
•4•10
=
1,2•10
м.
=
сТ
=
3•10
•4•10
=
1,2•10
м.
–?
Ответ: λ = 1,2•103 м.
3 3
Ответ:
λ =λ1,2•10
м. м.
Ответ:
= 1,2•10
© Гринкруг М.С., Ткачева Ю.И., Новгородов Н.А., 2022

5.

ЗАДАЧА №4
Колебательный контур радиоприемника настроен на частоту 15 МГц. Чему равна частота принимаемого сигнала, и во сколько раз
контур радиоприемника
настроен
частоту 15наМГц.
Чему
равна волны
частота5 м?
принимаемого сигнала, и во сколько раз
нужно Колебательный
изменить индуктивность
катушки в контуре,
чтобына
настроиться
сигнал
с длиной
Колебательный
контур
радиоприемника
настроен
на
частоту
15
МГц.
Чему
равна
частота
принимаемого
сигнала,
и во сколько
раз
нужно изменить индуктивность катушки
в контуре, чтобы
настроиться
на сигнал
с длиной
5 м?
8
Дано:
Колебательный
контур
радиоприемника
настроен
на волны
частоту
15 МГц.
Чему
равна
частота
принимаемого
сигнала, и во ск
c
3
10
6
нужно
изменить
индуктивность
катушки
в
контуре,
чтобы
настроиться
на
сигнал
с
длиной
волны
5
м?
8
Дано:
ν1 = 15 МГц = 15•10 Гц;
нужно изменить
катушки в контуре,
м? второго
20 м. 5Для
Решение.
Длина индуктивность
волны принимаемого
первом чтобы
случаенастроиться
сигнала: на
c с3 длиной
1086 волны
1 сигнал
Дано:
= 15
МГц = 15•106 Гц;
20
Решение.
Длина
волны
принимаемого
в
первом
случае
сигнала:
м.
Для
второго
15
10
λν21 =
5 м;
Дано:
1
c
3 10 6
1
6
c
3 108
8
6
νсλ12=
==3•10
15
МГц
=
15•10
Гц;
20
Решение.
Длина
волны
принимаемого
в
первом
случае
сигнала:
м.
Для
второго
15
10
5 м;
1
м/с
ν1 = 15 МГц = 15•10 Гц;
20 м. Для
сигнала: 1
8
c
c Решение.
3 108 Длина волны принимаемого 1в первом
1 15случае
106
λνс22=
=– 3•10
1 15 106
λ2 = 5 м; 2 c , 2 c 3 108 60 МГц.
?5 м;8 м/с
случая:
сν2=–3•10
5 8 60 МГц.
случая:
с = 3•108 м/с
c2 3 10
L2 ? м/с
2 c2 , 2
c
c 3 108
νL
5
,
60
случая:
МГц.
2 – ?– ?
2
2
ν
–
?
2
2
,
60 МГц.
случая:
2
2
2
2
1 2 1 2L2 51
5
LL21 – ?
, 1 L2 1 индуктивность
Но
надо
уменьшить в 16 раз.
2
2
L2
1
L1 – ?
– ? 2 1 LC ,
L
4
Но
индуктивность
надо
уменьшить в 16 раз.
2
1
L
1
L1
1 надо
L2 уменьшить
1
1
L1 2 LC , 12 L21 Но
4 индуктивность
Но
в 16 раз.
,
индуктивность
надо уменьшить в 16 раз.
L2 1
L
4
2
LC
2
1
L
4
2 LC
Ответ: ν2 = 60 МГц, L2 1 .
2
1
Ответ: ν2 = 60 МГц, LL1 16
1 .
L
1
Ответ: ν2 = 60 МГц, L21 16Ответ:
.
ν2 = 60 МГц, 2
.
L1
16
L1
16
© Гринкруг М.С., Ткачева Ю.И., Новгородов Н.А., 2022