Похожие презентации:
Плоская геометрическая фигура
1.
2.
1 группа• Любая плоская
геометрическая фигура
имеет площадь
• Площадь фигуры равна
сумме площадей частей, на
которые она разбивается
• Все высоты остроугольного
треугольника лежат внутри
треугольника
• Высоты тупоугольного
треугольника, проведенные
из вершин острых углов ,
лежат вне треугольника
2 группа
3 группа
• Эта площадь –
единственная
• Площадь любой
• Площадь треугольника
геометрической фигуры
равна половине
выражается
произведения его стороны
положительным числом
на высоту , опущенную на
эту сторону
• Площадь прямоугольного
треугольника равна
• Высоты прямоугольного
треугольника , проведенные половине произведения
его катетов
из вершин острых углов,
совпадают с катетами
• Высота, проведенная из
треугольника
вершины прямого угла,
лежит внутри
• Высота , проведенная из
треугольника
вершины тупого угла,
лежит внутри треугольника
3.
sin( ) sinsin
4.
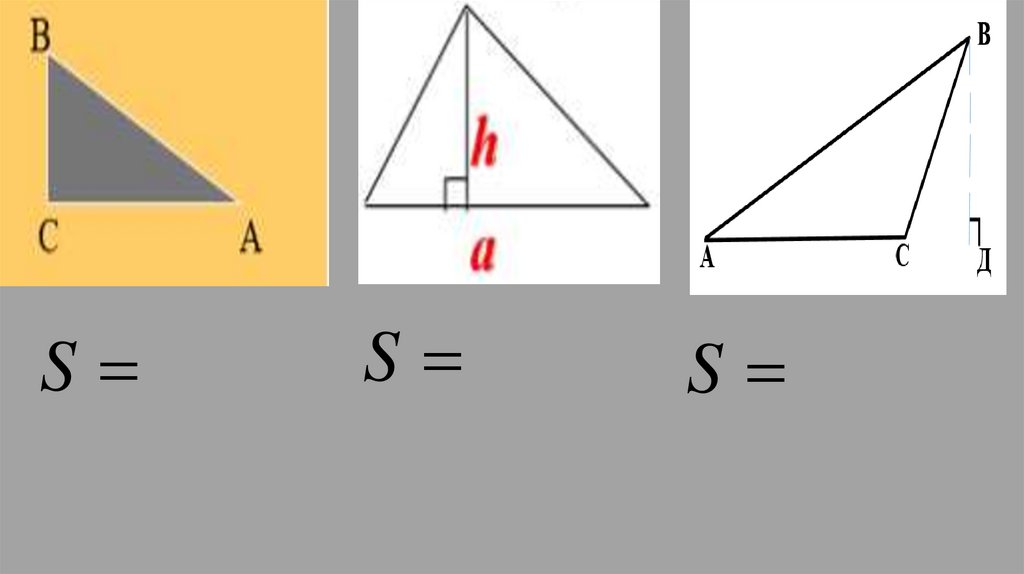
SS
S
5.
6.
Классная работаТЕОРЕМА О
ПЛОЩАДИ
ТРЕУГОЛЬНИКА
20.10.22
7.
ТЕОРЕМА О ПЛОЩАДИ ТРЕУГОЛЬНИКАПлощадь треугольника равна
половине произведения двух его
сторон на синус угла между ними.
8.
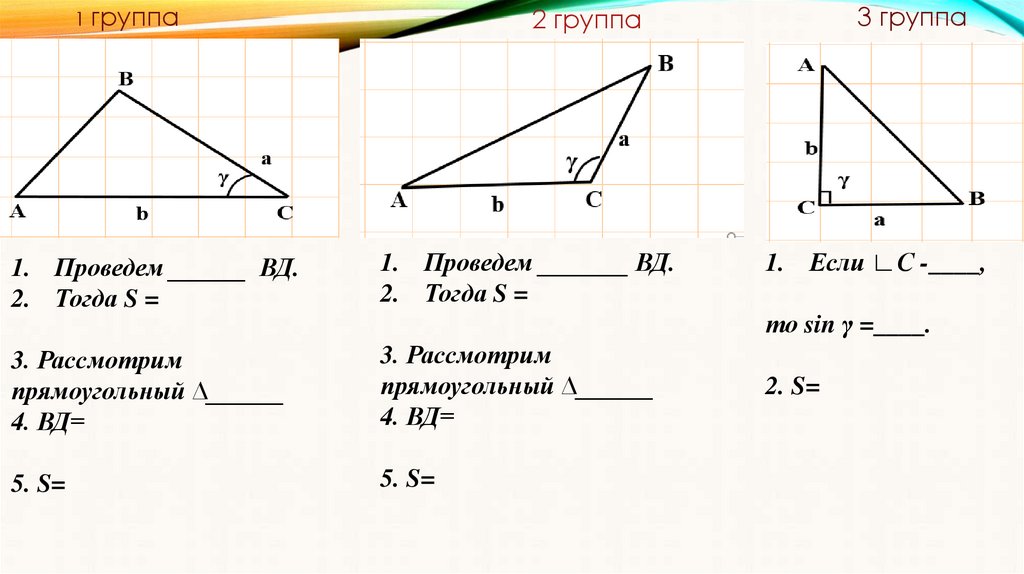
1 группа3 группа
2 группа
1. Проведем ______ ВД.
2. Тогда S =
1. Проведем _______ ВД.
2. Тогда S =
3. Рассмотрим
прямоугольный ∆______
4. ВД=
3. Рассмотрим
прямоугольный ∆______
4. ВД=
5. S=
5. S=
1. Если ∟С -____,
то sin γ =____.
2. S=
9.
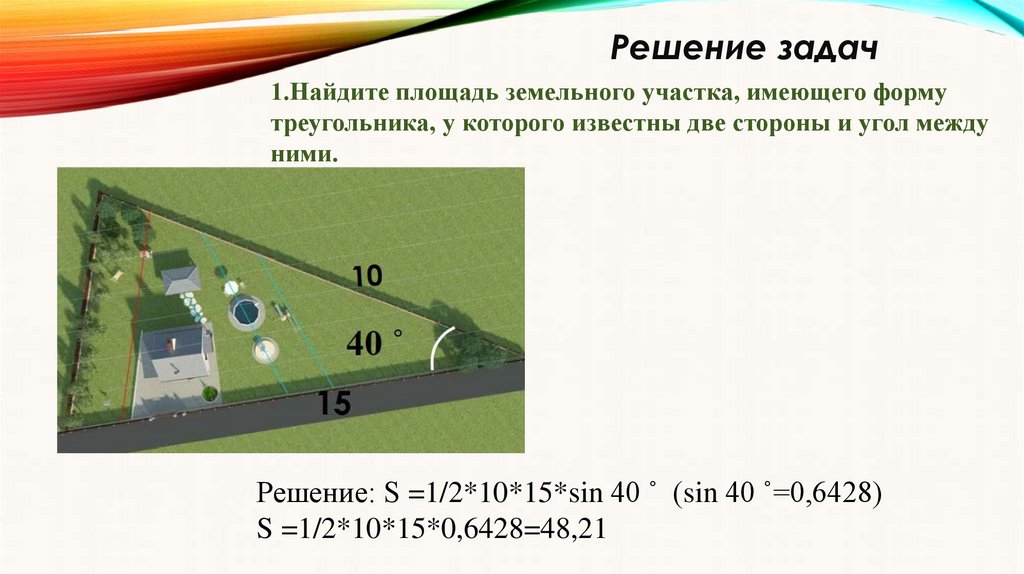
Решение задач1.Найдите площадь земельного участка, имеющего форму
треугольника, у которого известны две стороны и угол между
ними.
Решение: S =1/2*10*15*sin 40 ˚ (sin 40 ˚=0,6428)
S =1/2*10*15*0,6428=48,21
10.
17 задание ОГЭ1.В треугольнике одна из сторон равна 10, другая
равна 10√2, а угол между ними равен 135°. Найдите
площадь треугольник.


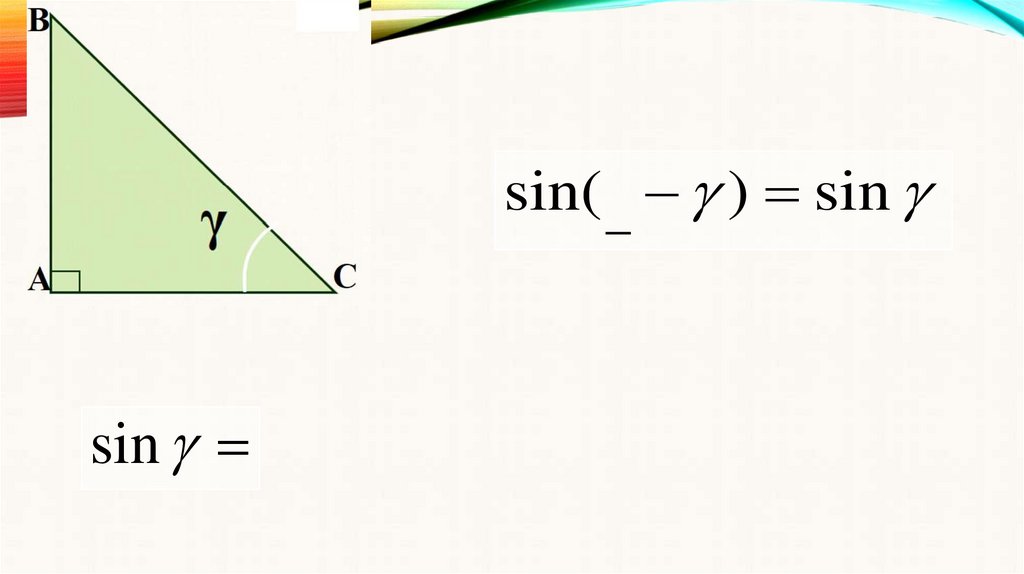




 Математика
Математика








