Алгебра из глубины веков… Урок-конференция

1. АЛГЕБРА ИЗ ГЛУБИНЫ ВЕКОВ…

Урок-конференция

2. План конференции

Исторический экскурс и теория решения
уравнений
Язык алгебры – уравнение. Перевод «с родного
языка на язык алгебры»
Решение исторических задач на составление
уравнения

3.

Алгебра – один из важнейших
разделов математики, который
помогает решать сложные задачи,
встречающиеся в науке, технике и
практической жизни.
Уравнения умели решать еще в
Вавилоне, Индии и Древней
Греции. Древнегреческий
математик Диофант умел решать
уравнения и даже применял буквы
для обозначения неизвестных.
Диофант Александрийский – III в.

4.

Но по-настоящему метод решения
уравнений был сформулирован
арабскими учеными.
Первым книгу о решении уравнений
написал на арабском языке Ал-Хорезми
Мухаммед бен-Муса (783-850).
Название у нее было очень странным –
«Краткая книга об исчислении алджабры и ал-мукабалы» («Китаб алджабр ва-л-мукабала». Трактат,
написанный в IX в., явился первым в
мире самостоятельным сочинением по
алгебре.
Ал-Хорезми Мухаммед бен-Муса (783-850)

5.

Для ал-Хорезми алгебра – это
искусство решения уравнений,
необходимое людям «в случае
наследования, наследованных
пошлин, раздела имущества,
торговли и во всех деловых
взаимоотношениях или же в случае
измерения земель, проведения
каналов, геометрических
вычислений и других предметов
различного рода».
В его трактате впервые прозвучало
хорошо известное нам слово
«алгебра». Что же означают слова
«ал-джабра» и «ал-мукабала»?
Ал-Хорезми Мухаммед бен-Муса (783-850)

6.

Ал-джабра
При решении уравнения
Если в части одной,
Безразлично какой,
Встретится член отрицательный,
Мы к обеим частям,
С этим членом сличив,
Равный член придадим,
Только с знаком другим
- И найдем результат нам желательный

7. Ал-мукабала

Дальше смотрим на уравнение,
Можно ль сделать приведенье,
Если члены в нем подобны,
Сопоставить их удобно,
Вычтя равный член из них,
К одному приводим их.

8. Ал-джабра

Таким образом, «ал-джабра» называлась операция
переноса отрицательных членов из одной части
уравнения в другую, но уже с положительным знаком.
По-русски это слово означает «восполнение».
В те времена отрицательные числа считались
абсурдными, фиктивными. Перенесение же их с
противоположным знаком в другую часть уравнения и
превращение их таким образом в положительные числа
как бы восстанавливало их, превращало в настоящие
числа.

9. Ал-мукабала

Слово «ал-мукабала» означало приведение
подобных членов. В отличие от слова «ал-джабра»,
которое в форме «алгебра» стало одним их самых
употребительных в математике, про «ал-мукабалу»
помнят только историки науки.
Какие же операции мы выполняем при решении
уравнения 6х – 13 = 2х -5 ?

10. Решение исторических задач с помощью уравнений

«Чтобы решить вопрос, относящийся к
числам или отвлеченным отношениям
величин, нужно лишь перевести задачу с
родного языка на язык алгебраический», писал великий Ньютон.
Как именно выполняется такой перевод,
Ньютон показал на примерах.
Вот одни из них.
Исаак Ньютон

11. Решение исторических задач с помощью уравнений

Купец имел некоторую сумму денег.
В первый год он истратил 100 фунтов.
К оставшейся части добавил третью ее часть.
В следующем году он вновь истратил 100
фунтов. И увеличил оставшуюся сумму на
третью ее часть. В третьем году он опять
истратил 100 фунтов. После того, как он добавил
к остатку третью его часть, капитал стал вдвое
больше первоначального.

12.

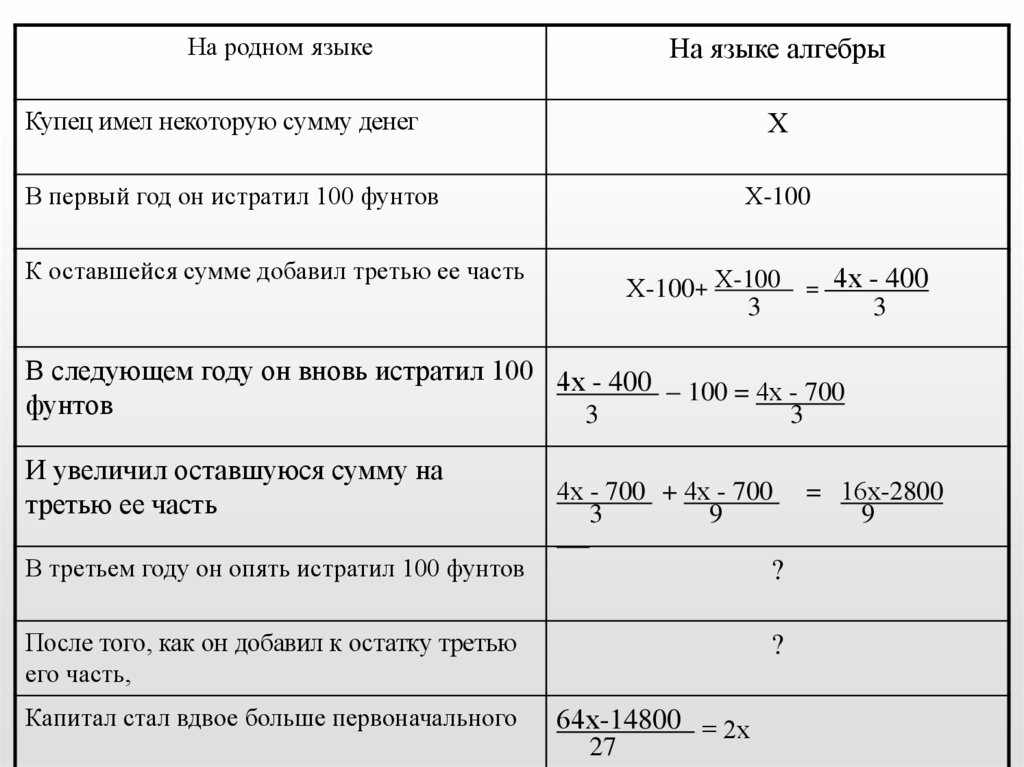
На родном языке
На языке алгебры
Купец имел некоторую сумму денег
Х
В первый год он истратил 100 фунтов
Х-100
К оставшейся сумме добавил третью ее часть
Х-100+ Х-100 = 4х - 400
3
3
В следующем году он вновь истратил 100 4х - 400 _
100 = 4х - 700
фунтов
3
3
И увеличил оставшуюся сумму на
третью ее часть
4х - 700 + 4х - 700
3
9
В третьем году он опять истратил 100 фунтов
?
После того, как он добавил к остатку третью
его часть,
?
Капитал стал вдвое больше первоначального
64х-14800 = 2х
27
= 16х-2800
9

13. Практически не сохранилось фактов биографии замечательного древнегреческого математика Диофанта. Все, что известно о нем,

получено из надписи на его надгробии, составленной в форме
математической задачи.
Диофант из Александрии
Путник! Здесь прах погребен Диофанта.
И числа поведать могут, о чудо,
сколь долог был век его жизни.
Часть шестую его представило
прекрасное детство.
Двенадцатая часть протекла еще жизни –
покрылся пухом тогда подбородок.
Седьмую в бездетном браке провел Диофант.
Прошло пятилетье, он был осчастливлен
Рожденьем прекрасного первенца сына,
Коему рок половину лишь жизни прекрасной
и светлой дал на земле по сравненью с отцом.
В печали глубокой старец земного удела
конец восприял, переживши года четыре
с тех пор, как сына лишился.
Скажи, сколько лет жизни достигнув,
смерть восприял Диофант.

14. В XI веке происходит захват и разорение мусульманами Северной Индии (Махмуд Газневи). Культурные центры переносятся в Южную

Индию. Научная жизнь на длительный период угасает. Из значительных
фигур этого периода можно выделить Бхаскару, автора астрономоматематического трактата «Сиддханта-широмани».
Задача Бхаскары
Из множества чистых цветков лотоса
были принесены в жертву:
Шиве – третью долю этого множества,
Вишпу – пятую,
Солнцу – шестую,
Четвертую долю получил Бхавани,
А остальные шесть цветков получил уважаемый учитель.
Сколько было цветков?
Решение. Пусть было х цветков, тогда

15. При огромном участии Петра I в России выходит первый отечественный учебник по математике. Идет 1703 год. Леонтий Филиппович

Магницкий издает "Арифметику".
"Арифметика, сиречь наука числительная.
С разных диалектов на славянский язык
переведенная, и воедино собрана и на две части
разделенная"
Труд Леонтия Филипповича не был
переводным, аналогов учебника в то время не
существовало. Это была уникальная книга.
"Арифметика или числительница, есть
художество честное, независтное, ..."
Леонтий Филиппович Магницкий

16. Из «Арифметики» Магницкого

Некий человек нанял работника на год, обещая ему
дати 12 рублей и кафтан. Но тот, проработав 7 месяцев,
востотел уйти и просил достойные платы с кафтаном; он
же дади ему по достоинству расчет 5 рублей и кафтан, и
ведательно есть, коликой цены оный кафтан был.
Решение. Пусть кафтан стоил х рублей, если бы работник
отработал год, то за 1 месяц оплата составила бы А так как он отработал 7 месяцев, то оплата за 1 месяц
составила –
Приравняв эти отношения, используем свойство пропорции
и решим уравнение

17. В рассказе «Репетитор» великий русский писатель А.П.Чехов приводит следующую задачу:

Купец купил 138 аршин черного и
синего сукна за 540 рублей.
Спрашивается, сколько аршин он купил
того и другого, если синее сукно стоило 5
рублей за аршин, а черное 3 рубля?
Решение. Пусть было х аршин синего
сукна, тогда черного -

18. Старинная русская задача

Вопросил некто некоего учителя: «Сколько имеешь
учеников у себя, так как я хочу отдать сына к тебе в
училище». Учитель ответил: «Если ко мне придет
учеников еще столько же, сколько имею, и полстолько, и
четвертая часть, и твой сын, тогда у меня учеников 100».
Сколько же было у учителя учеников?
Решение: Пусть у учителя было х учеников.