Похожие презентации:
Уравнение касательной
1.
КасательнаяУравнение касательной
2.
Используя формулы и правила дифференцирования,найдите производные следующих функций:
1. у 2 х10
у 20х 9
2. у 2 х
у
3. у 7 х 4
у 7
4. у tgx 5 x
у
5. у х 3 sin x
у 3х 2 cos x
1
х
1
5
2
cos x
3.
Сf'(1)=?
Я
f' (2)=?
Ю
f' (2)=?
Ф
f' (4)=?
К
f' (2)=?
И
f' (-1)=?
Л
f' (-2)=?
1
24
65
23
Ф л ю к
6
-18 -1/4
с и я
4. История возникновения названия
Немецкий математикЛейбниц
Английский ученый
Ньютон
5. Согласны ли вы с утверждением:
Касательная – это прямая,имеющая с данной кривой
одну общую точку
6.
yy = 2х - 1
y = x2
1
x
х =1
7.
1.Дать определение касательной.2.Ввести уравнение касательной.
3.Составить алгоритм нахождения
уравнения касательной к графику
функции.
4.Научится
решать
задачи
на
нахождение уравнения касательной.
8.
yy = 2х - 1
y = x2
1
x
х =1
Касательная – предельное
положение секущей
9.
y=kx+bk- угловой коэффициент
k = tgα
f´(x) = tgα
10.
yy=kx+b
M(a;f(a))
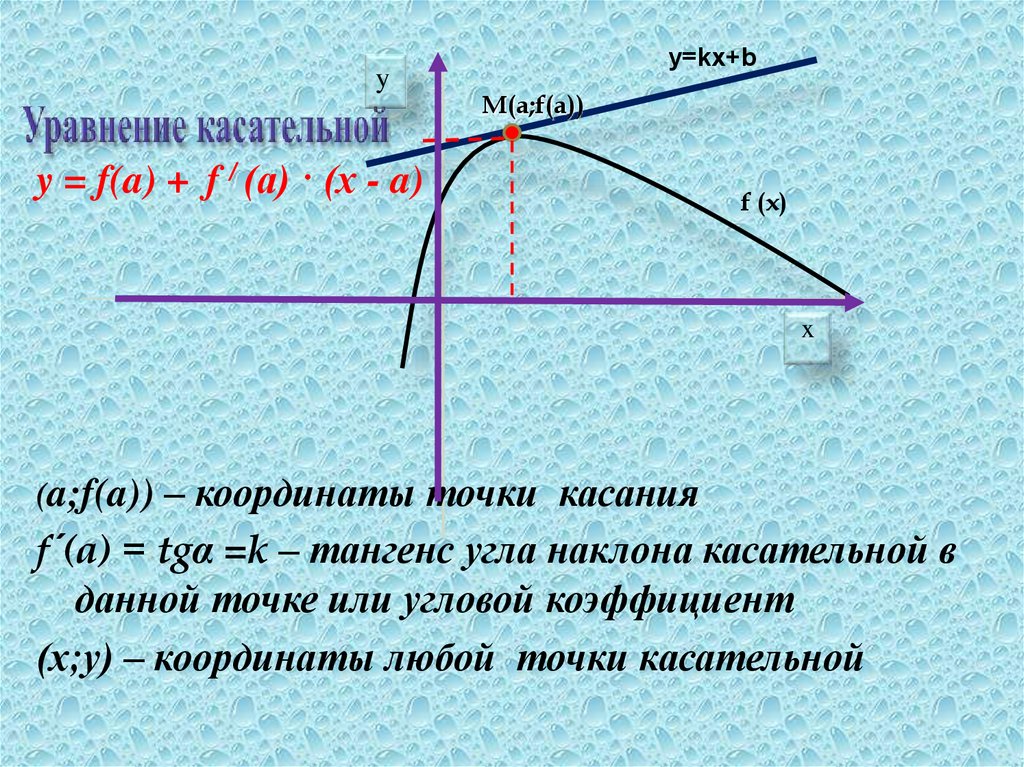
y = f(a) + f / (a) · (x - a)
f (x)
x
(a;f(a)) – координаты точки касания
f´(a) = tgα =k – тангенс угла наклона касательной в
данной точке или угловой коэффициент
(х;у) – координаты любой точки касательной
11. Алгоритм
1. Обозначим абсциссу точки касаниябуквой а
2. Вычислим f(а)
3. Найдем f´(x) и вычислим f´(а)
4. Подставим найденные значения в общее
уравнение касательной:
y = f(a) + f / (a) · (x - a)
5. Запишем уравнение в виде y kx b
12. Потренируемся:
1. Составить уравнение касательной к4
3
графику
функции f ( x) x 7 x 12 x 45
в точке с абсциссой а = 0.
Образец оформления и решения
смотрите ниже
13.
14. Потренируемся:
Решить самостоятельно2. Составить уравнение касательной к
графику функции f(x)=x²-3x+5 в точке
с абсциссой x = -1.
15. Напишите уравнение касательной к графику функции у=f(x) в точке с абсциссой а:
3. f(x) = х²+ х+1, а=1.4. f(x)= х-3х², а=2.








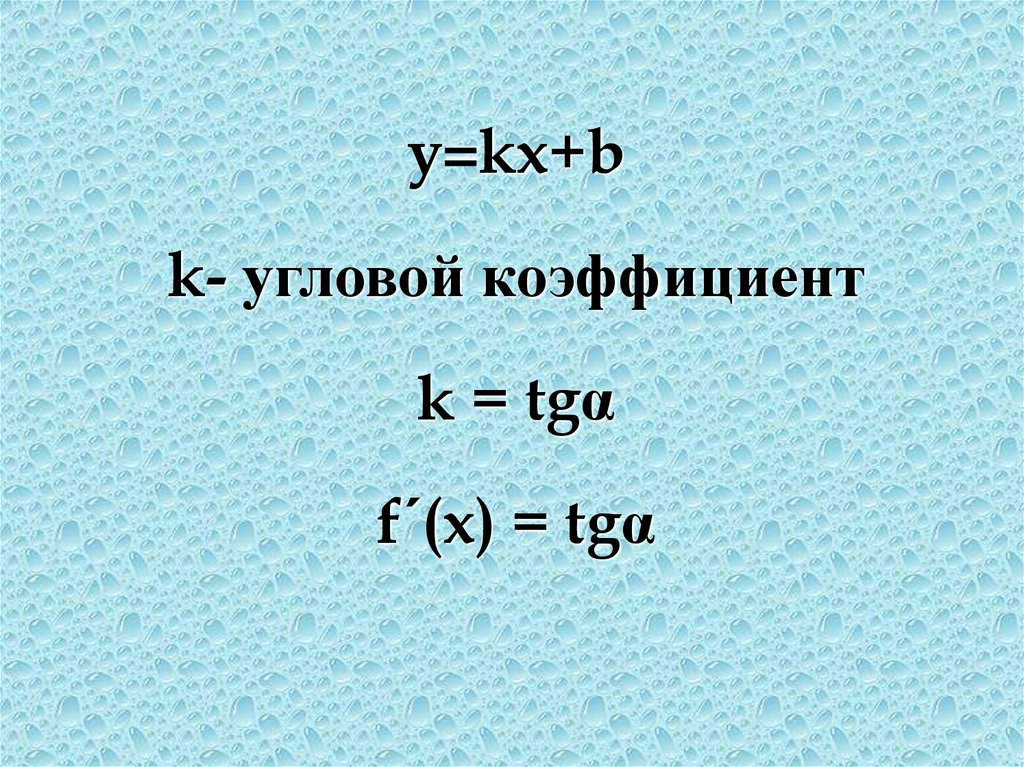





 Математика
Математика








