Похожие презентации:
Исследование функций
1. Лекция Исследование функций
1 План исследования функций2 Возрастание и убывание. Точки экстремума
3 Выпуклость и вогнутость, точки перегиба
4 Асимптоты графика функций
5 Построение графиков функций
19 февраля 2024 г.
2. Эпиграф
Следует помнить, что в каком-тосмысле высшая математика проще
элементарной.
Исследовать,
например,
лесную
чащу пешком очень трудно, с
самолета это делается проще.
У.Сойер
Английский математик и педагог
Иванов О.В., Кудряшова Л.В., 2005
2
3. 1. План исследования функций
Подход к исследованию функций19 февраля 2024 г.
4. Цели исследования функций
Исследование функции проводят для того, чтобы описать припомощи текста и (или) графически поведение функции для всех
возможных значений аргумента.
Исследование функций проводят в несколько стадий.
Иванов О.В., Кудряшова Л.В., 2005
4
5. План исследования функций
1. Найти область определения функции.2. Исследовать функцию на четность-нечетность.
3.Найти
точки
пересечения
с
осями
координат,
промежутки
знакопостоянства функции.
4. Найти асимптоты графика функции.
5. Найти экстремумы, интервалы возрастания и убывания.
6.Исследовать направление выпуклости графика функции, найти точки
перегиба.
7.Сводная таблица.
8. Эскиз графика.
Иванов О.В., Кудряшова Л.В., 2005
5
6. 2. Возрастание и убывание. Точки экстремума
Понятие возрастания (убывания) функцииНеобходимое и достаточное условия монотонности
Понятие экстремума
Необходимое и достаточное условия экстремума
19 февраля 2024 г.
7. Возрастание (убывание) функции
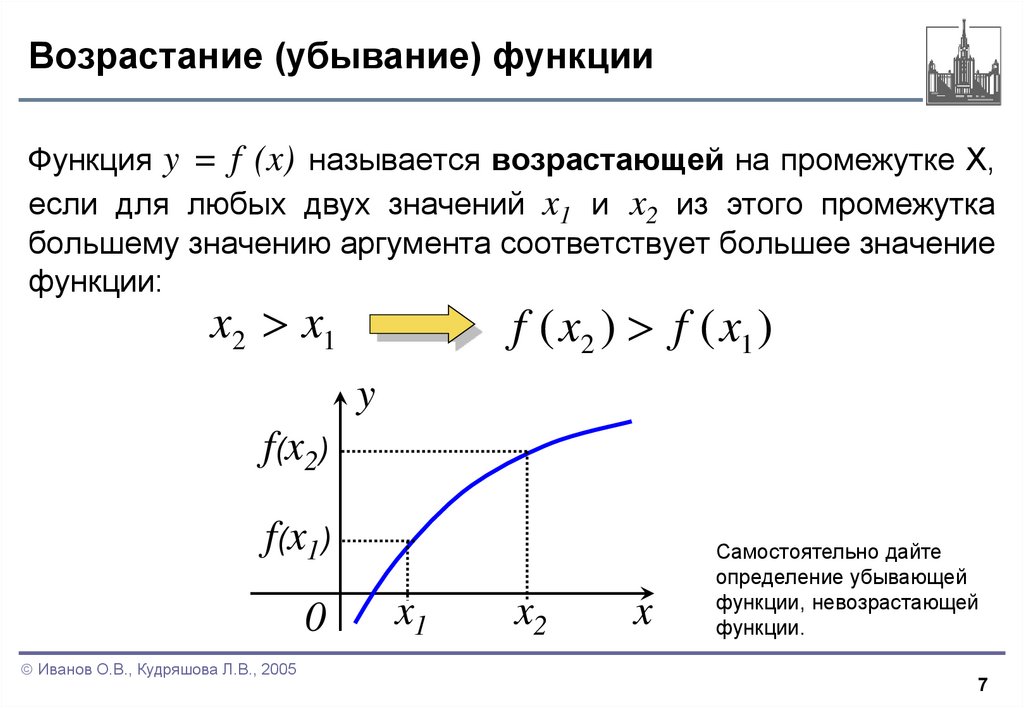
Функция y = f (x) называется возрастающей на промежутке X,если для любых двух значений x1 и x2 из этого промежутка
большему значению аргумента соответствует большее значение
функции:
x2 x1
f ( x2 ) f ( x1 )
y
f(x2)
f(x1)
0
Иванов О.В., Кудряшова Л.В., 2005
x1
x2
x
Самостоятельно дайте
определение убывающей
функции, невозрастающей
функции.
7
8. Достаточное условие монотонности
Теорема. Если производная дифференцируемой функцииположительна внутри некоторого промежутка X, то функция
возрастает в этом промежутке.
Доказательство. Выберем в этом промежутке два значения:
x2 x1
Для функции выполняются условия теоремы Лагранжа, поэтому:
f ( x2 ) f ( x1 ) f ( )( x2 x1 )
Поскольку производная положительна, то
И это означает, что
Иванов О.В., Кудряшова Л.В., 2005
f ( x2 ) f ( x1 ) 0
f ( x2 ) f ( x1 )
X
Самостоятельно
докажите, что если
производная
отрицательна, то
функция убывает.
8
9. Необходимое условие монотонности
Если функция возрастает на некотором промежутке X, топроизводная неотрицательна на этом промежутке:
f ( x ) 0
Если функция убывает на некотором промежутке X, то
производная неположительна на этом промежутке:
f ( x ) 0
Иванов О.В., Кудряшова Л.В., 2005
9
10. Экстремум функции
Точка x0 называется точкой максимума функции f (x), если внекоторой окрестности точки x0 выполняется неравенство:
f ( x ) f ( x0 )
Точка x1 называется точкой минимума функции f (x), если в
некоторой окрестности точки x1 выполняется неравенство:
f ( x ) f ( x1 )
Значения функции в точках минимума и максимума называются
минимумом и максимумом функции, или ее экстремумом.
Иванов О.В., Кудряшова Л.В., 2005
10
11. Почему надо находить экстремумы
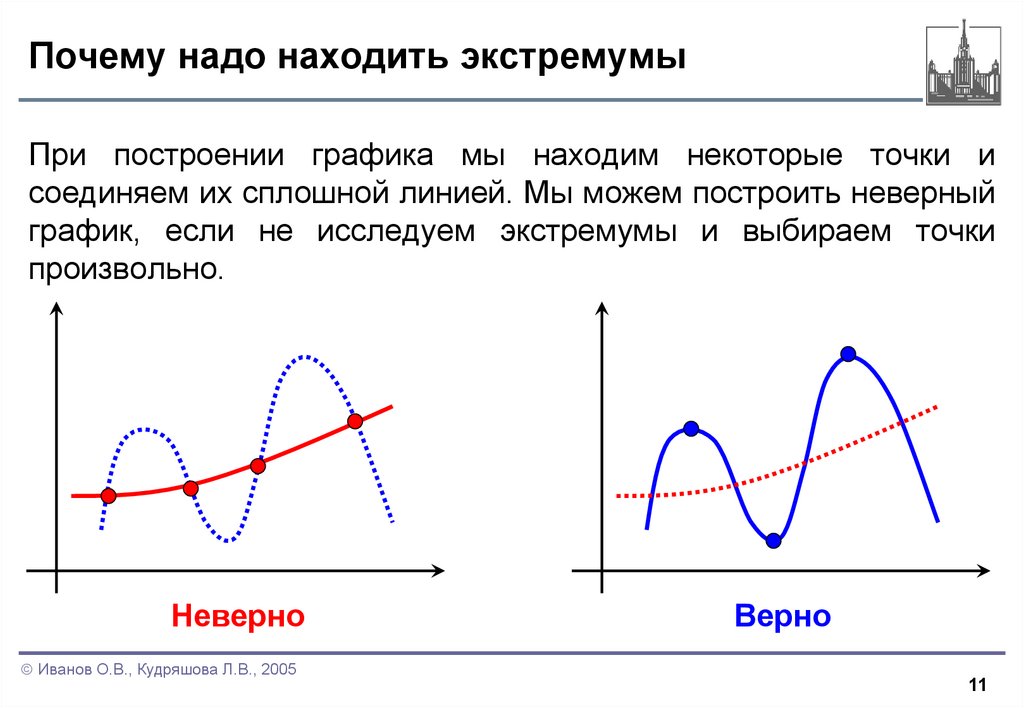
При построении графика мы находим некоторые точки исоединяем их сплошной линией. Мы можем построить неверный
график, если не исследуем экстремумы и выбираем точки
произвольно.
Неверно
Иванов О.В., Кудряшова Л.В., 2005
Верно
11
12. Необходимое условие экстремума
Теорема. Для того, чтобы функция f (x) имела экстремум вточке x0, необходимо, чтобы ее производная в этой точке
равнялась нулю или не существовала.
y 3 x2
y x3 1
y
Производная
существует и
равна нулю, а
экстремума нет
Точка экстремума
есть, а производная
не существует
x
Иванов О.В., Кудряшова Л.В., 2005
12
13. Достаточное условие экстремума
Теорема. Если при переходе через точку x0 производнаядифференцируемой функции y = f (x) меняет свой знак с плюса
на минус, то точка x0 есть точка максимума функции, а если с
минуса на плюс, – то точка минимума.
Доказательство. Пусть в некотором интервале (a, x0)
производная положительна, а в некотором интервале (x0, b)
отрицательна. Тогда функция в первом интервале возрастает, а
во втором убывает. Это означает, что f (x) f (x0) для всех x
(a, b). Следовательно, это точка максимума. Для минимума
доказательство аналогично.
Иванов О.В., Кудряшова Л.В., 2005
13
14. Схема исследования экстремумов
1. Находим производную.2.Определяем критические точки функции (в которых
производная равна нулю или не существует).
3.Отмечаем на числовой оси критические точки и находим знак
производной в каждом из интервалов области
определения. Находим точки экстремума.
4.Вычисляем экстремумы (значение функции в точках
экстремума).
–
+
max
Иванов О.В., Кудряшова Л.В., 2005
+
min
–
+
max
14
15. 3. Выпуклость графика функции. Точки перегиба
Понятие выпуклостиДостаточное условие выпуклости
Точки перегиба
Достаточное условие перегиба
19 февраля 2024 г.
16. Выпуклость графика функции
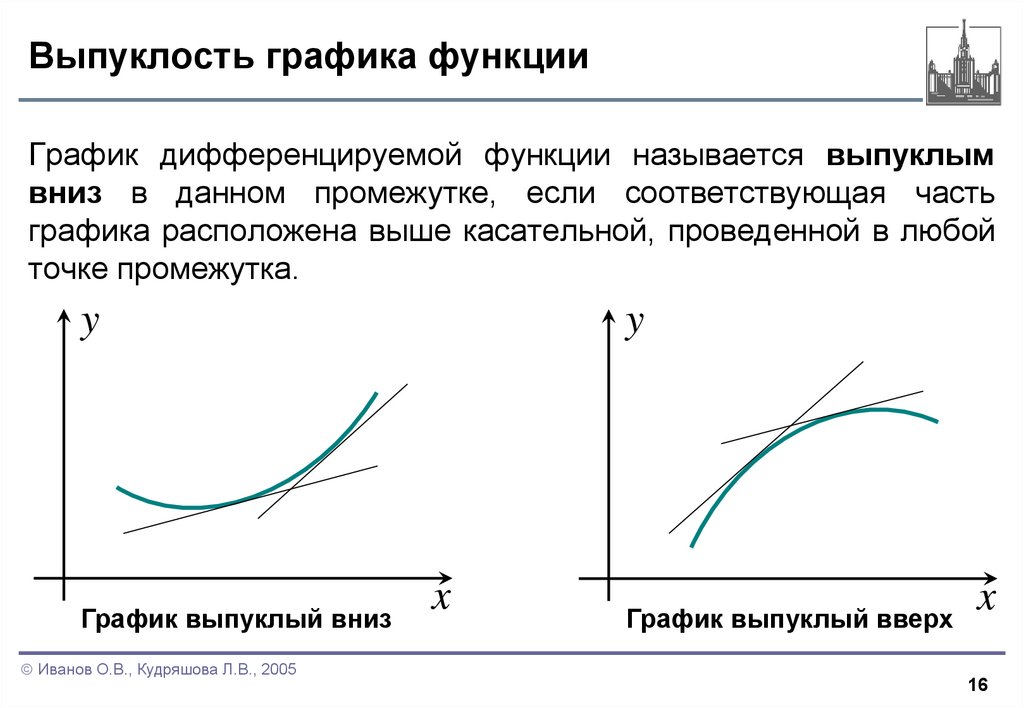
График дифференцируемой функции называется выпуклымвниз в данном промежутке, если соответствующая часть
графика расположена выше касательной, проведенной в любой
точке промежутка.
y
График выпуклый вниз
Иванов О.В., Кудряшова Л.В., 2005
y
x
x
График выпуклый вверх
16
17. Достаточное условие выпуклости
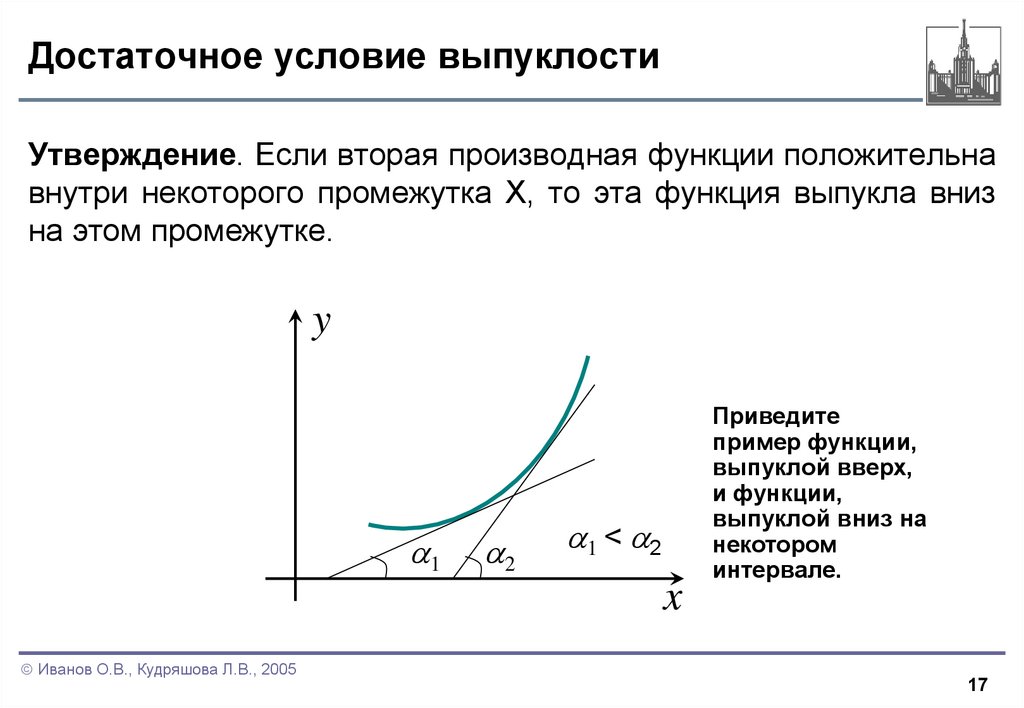
Утверждение. Если вторая производная функции положительнавнутри некоторого промежутка X, то эта функция выпукла вниз
на этом промежутке.
y
1
2
1 < 2
x
Иванов О.В., Кудряшова Л.В., 2005
Приведите
пример функции,
выпуклой вверх,
и функции,
выпуклой вниз на
некотором
интервале.
17
18. Точка перегиба
Точкой перегиба (inflection point) графика непрерывнойфункции называется точка, разделяющая интервалы, в которых
функция выпукла вниз и вверх.
Теорема
(необходимое
условие
перегиба).
Вторая
производная дважды дифференцируемой функции в точке
перегиба равна нулю:
f ( x ) 0
Иванов О.В., Кудряшова Л.В., 2005
18
19. Достаточное условие перегиба
Теорема.Если
вторая
производная
дважды
дифференцируемой функции при переходе через некоторую
точку x0 меняет знак, то x0 есть точка перегиба графика.
Точка перегиба
Отметим также, что если критическая
точка дифференцируемой функции
не является точкой экстремума, то
она есть точка перегиба.
Иванов О.В., Кудряшова Л.В., 2005
19
20. Схема исследования на выпуклость
1. Находим вторую производную функции.2.Определяем точки, в которых вторая производная равна нулю
или не существует.
3.Определяем знак второй производной в каждом из
интервалов. Находим точки перегиба.
4.Находим значение функции в точках перегиба.
–
Иванов О.В., Кудряшова Л.В., 2005
перегиб
+
+
перегиб
20
21. 4. Асимптоты графика функций
Вертикальные асимптотыГоризонтальные асимптоты
Наклонные асимптоты
19 февраля 2024 г.
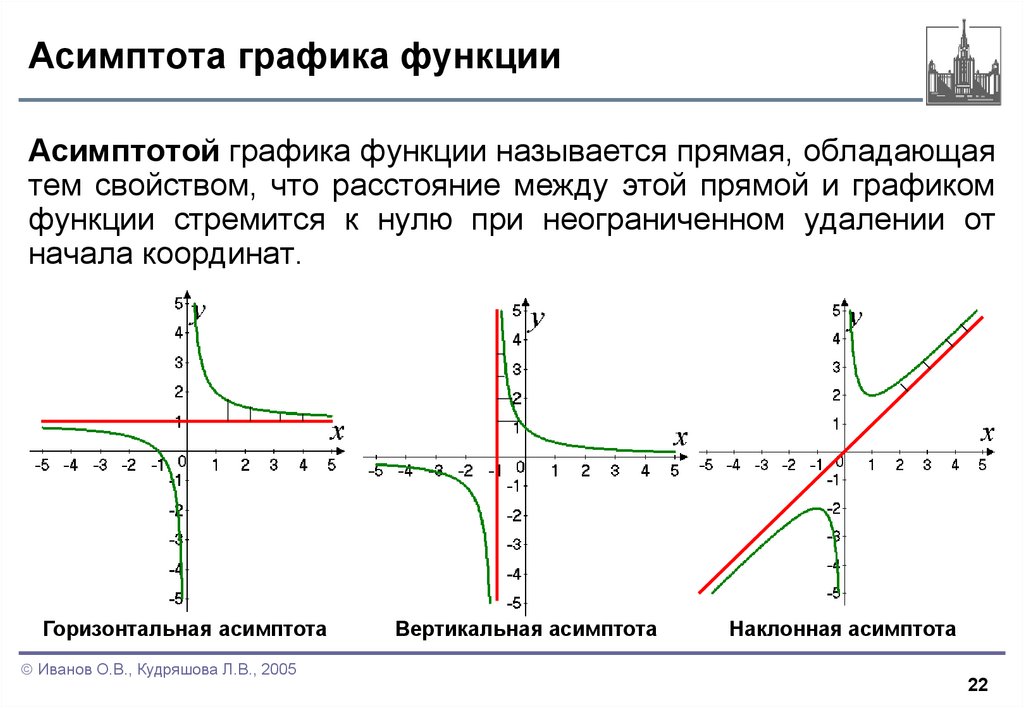
22. Асимптота графика функции
Асимптотой графика функции называется прямая, обладающаятем свойством, что расстояние между этой прямой и графиком
функции стремится к нулю при неограниченном удалении от
начала координат.
Горизонтальная асимптота
Иванов О.В., Кудряшова Л.В., 2005
Вертикальная асимптота
Наклонная асимптота
22
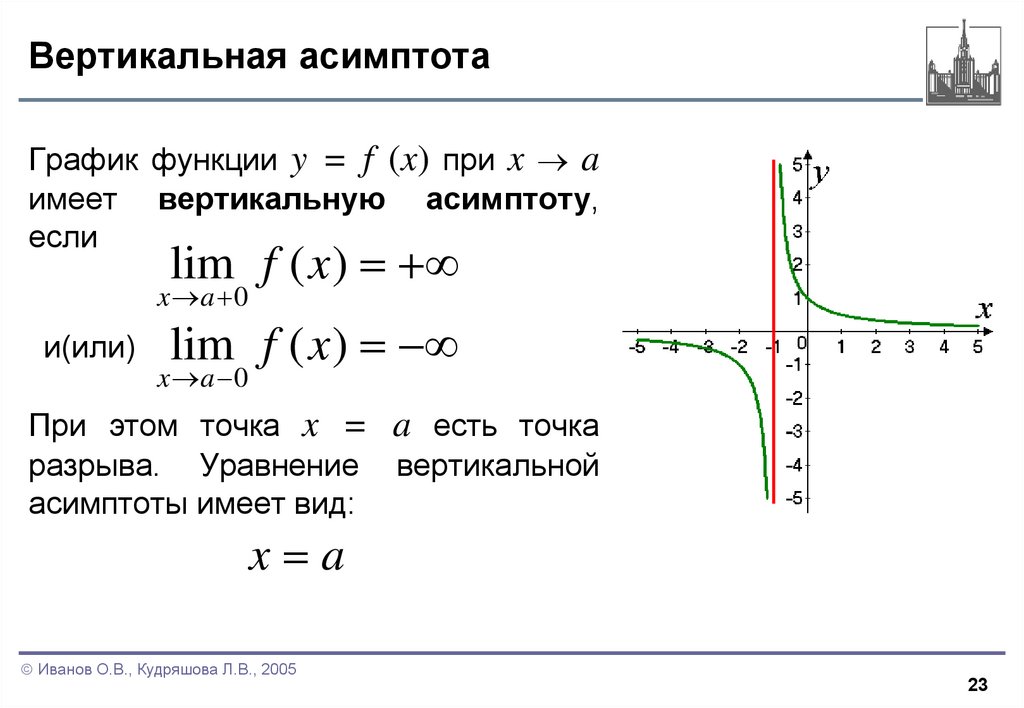
23. Вертикальная асимптота
График функции y = f (x) при x aимеет вертикальную асимптоту,
если
lim f ( x )
x a 0
и(или)
lim f ( x )
x a 0
При этом точка x = a есть точка
разрыва. Уравнение вертикальной
асимптоты имеет вид:
x a
Иванов О.В., Кудряшова Л.В., 2005
23
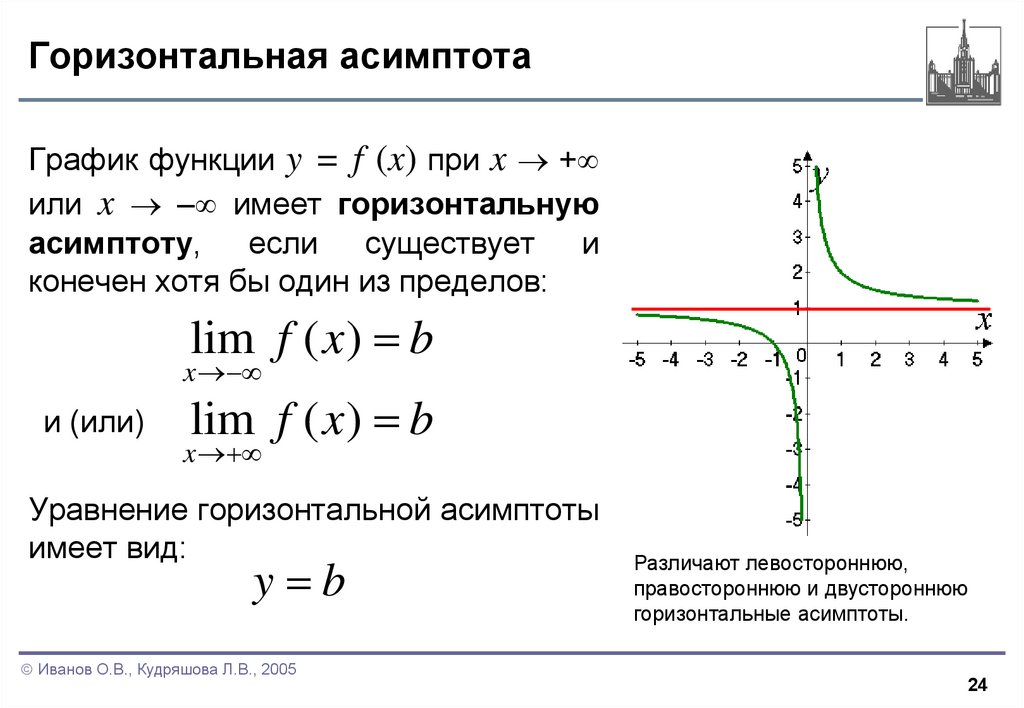
24. Горизонтальная асимптота
График функции y = f (x) при x +или x – имеет горизонтальную
асимптоту, если существует и
конечен хотя бы один из пределов:
lim f ( x) b
x
и (или)
lim f ( x) b
x
Уравнение горизонтальной асимптоты
имеет вид:
y b
Иванов О.В., Кудряшова Л.В., 2005
Различают левостороннюю,
правостороннюю и двустороннюю
горизонтальные асимптоты.
24
25. Наклонная асимптота
Наклонной асимптотойфункции называется
задаваемая уравнением
графика
прямая,
y kx b
Для ее существования необходимо,
чтобы
существовали
конечные
пределы:
f ( x)
lim
k
x
x
lim f ( x ) kx b
x
Иванов О.В., Кудряшова Л.В., 2005
Различают левостороннюю,
правостороннюю и двустороннюю
наклонные асимптоты.
25
26. Схема отыскания асимптот
1. Вертикальные асимптоты. Если в точке разрыва функцииили граничной точке области определения хотя бы один
односторонний предел бесконечен, то в этой точке есть
вертикальная асимптота.
2. Горизонтальные асимптоты. Если предел функции в
конечен, то получаем уравнение горизонтальной асимптоты.
3. Наклонные асимптоты. Если в в конечного предела нет,
то ищем пределы для наклонной асимптоты. Если
соответствующие пределы конечны, то получаем уравнение
наклонной асимптоты.
Иванов О.В., Кудряшова Л.В., 2005
26
27. 5. Построение графиков
Примеры построения графиков19 февраля 2024 г.
28. Исследование функции
y x 3x 13
Исследование функции
2
1) Область определения
D f ;
2) Точки пересечения с осями координат
x 0 y 1
3) Функция ни четная, ни нечетная
4) Экстремумы и монотонность
2
y 3x 6 x
3x 6 x 0
x2 2x 0
x x 2 0
x 0; x 2
2
Иванов О.В., Кудряшова Л.В., 2005
-
+
0
f max 0 1
+
2
f min 2 3
28
29. Построение графика функции
y x 3x 13
2
y
1
0
Иванов О.В., Кудряшова Л.В., 2005
1
x
29
30. Исследование функции
1 4y x 4x2 6
2
Исследование функции
D f ;
1) Область определения
2) Точки пересечения с осями координат
x 0 y 6
3) Функция четная
4) Экстремумы и монотонность
y 2 x 3 8 x
2 x3 8x 0
x3 4 x 0
x x 2 x 2 0
x 0; x 2; x 2
Иванов О.В., Кудряшова Л.В., 2005
-
-
+
-2
0
f min 2 2
+
2
f max 0 6
30
31. Построение графика функции
1 4y x 4x2 6
2
y
1
0
Иванов О.В., Кудряшова Л.В., 2005
1
x
31
32. Пример
Дана функцияНеобходимо исследовать эту функцию и
построить ее график
Иванов О.В., Кудряшова Л.В., 2005
32
33. Решение
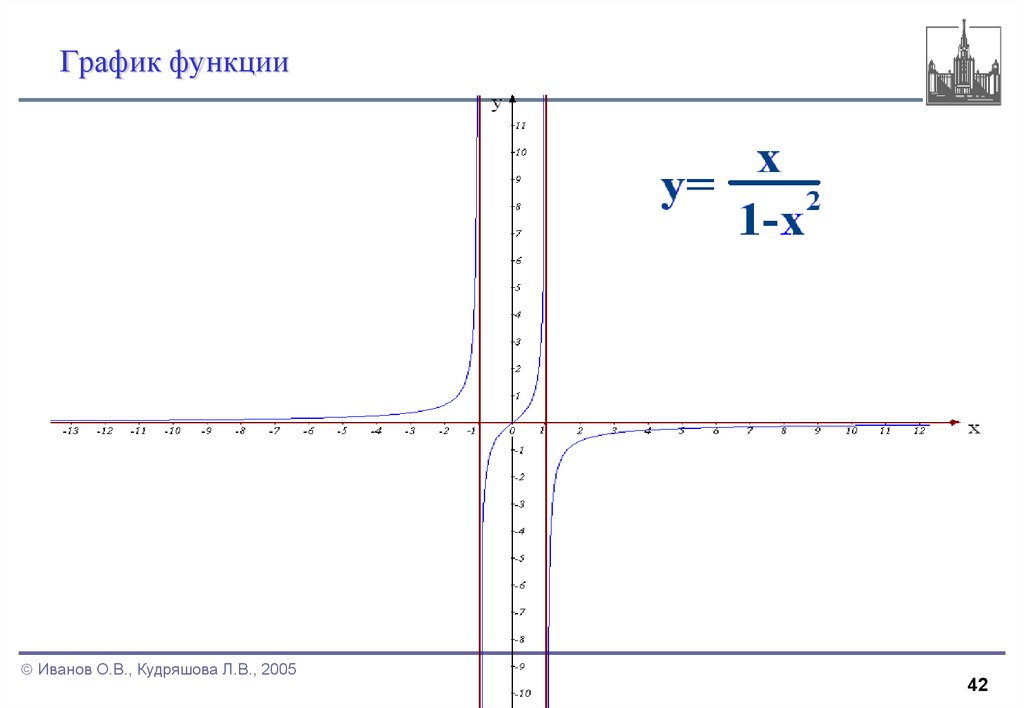
1. Найти область определения функцииФункция не определена при x = 1 и x = -1.
Область ее определения состоит из трех
интервалов (-∞; -1), (-1; 1), (1; +∞), а график из
трех ветвей.
Иванов О.В., Кудряшова Л.В., 2005
33
34. 2. Выяснить, является ли функция четной, нечетной или общего вида
Функция является нечетной, т.к.Следовательно, график ее симметричен относительно начала
координат.
Для построения графика достаточно исследовать ее при x ≥ 0
Иванов О.В., Кудряшова Л.В., 2005
34
35. 3. Найти (если это можно) точки пересечения графика функции с осями координат
Если x = 0, то y = 0. График пересекает ось Oy в точке O(0;0).Если y = 0, то x = 0. График пересекает ось Ox в точке O(0;0).
Иванов О.В., Кудряшова Л.В., 2005
35
36. Найти интервалы знакопостоянства функции (промежутки, на которых f(x)>0 или f(x)<0)
Найти интервалы знакопостоянства функции(промежутки, на которых f(x)>0 или f(x)<0)
Функция знакоположительна (y>0) на интервалах (-∞; -1) и
(0; 1).
Функция знакоотрицательна (y<0) на интервалах (-1; 0) и (1;
+∞).
Иванов О.В., Кудряшова Л.В., 2005
36
37. 4. Найти асимптоты графика функции
Прямые x = 1 иасимптотами.
x = -1 являются ее вертикальными
Прямая у = 0 является ее горизонтальной асимптотой.
Иванов О.В., Кудряшова Л.В., 2005
37
38. 5. Найти интервалы монотонности функции
Находим интервалы возрастания и убывания функции. Т.к.,
то
> 0 в области определения, и функция является возрастающей на
каждом интервале области определения.
Иванов О.В., Кудряшова Л.В., 2005
38
39. Найти экстремумы функции
Находим,
интервалы
возрастания
и
убывания
функции.
Т.к.
то критическими точками являются точки
x1 = 1 и x2 = -1 (
не
существует), но они не принадлежат области определения функции.
Функция экстремумов не имеет.
Иванов О.В., Кудряшова Л.В., 2005
39
40. 6. Найти интервалы выпуклости и точки перегиба графика функции
Исследуем функцию на выпуклость. НаходимИванов О.В., Кудряшова Л.В., 2005
:
40
41.
Вторая производная равна нулю или не существует в точках x1= 0, x2 = -1 и x3 = 1.
Точка О(0; 0) – точка перегиба графика функции.
График выпуклый вверх на интервалах (-1; 0) и (1; +∞);
выпуклый вниз на интервалах (-∞; -1) и (0; 1).
Иванов О.В., Кудряшова Л.В., 2005
41
42. График функции
Иванов О.В., Кудряшова Л.В., 200542
43. Первый пример
Исследовать функциюРешение.
1. ОДЗ
2
x
y
x 3
x ( ;3) (3; )
2. Функция общего вида (не является четной, нечетной)
Иванов О.В., Кудряшова Л.В., 2005
43
44. Решение
2x
y
x 3
3. Пересечение с осями в единственной точке (0; 0)
4. Вертикальная асимптота:
x 3
Горизонтальных асимптот нет.
Иванов О.В., Кудряшова Л.В., 2005
44
45. Решение
Наклонная асимптота:2
x
x
y
k lim
1
x 3
x x ( x 3)
x2
b lim
x 3
x x 3
2
y kx b x 3
8. Строим график
Иванов О.В., Кудряшова Л.В., 2005
45
46. Решение
2x
y
x 3
5. Интервалы монотонности, экстремумы
x
2 x ( x 3) x 2 x ( x 6)
y
2
( x 3)
( x 3) 2
x 3
2
–
–
+
0
Иванов О.В., Кудряшова Л.В., 2005
3
+
6
46
47. 6. Точки перегиба, интервалы выпуклости и вогнутости графика функции.
Иванов О.В., Кудряшова Л.В., 200547
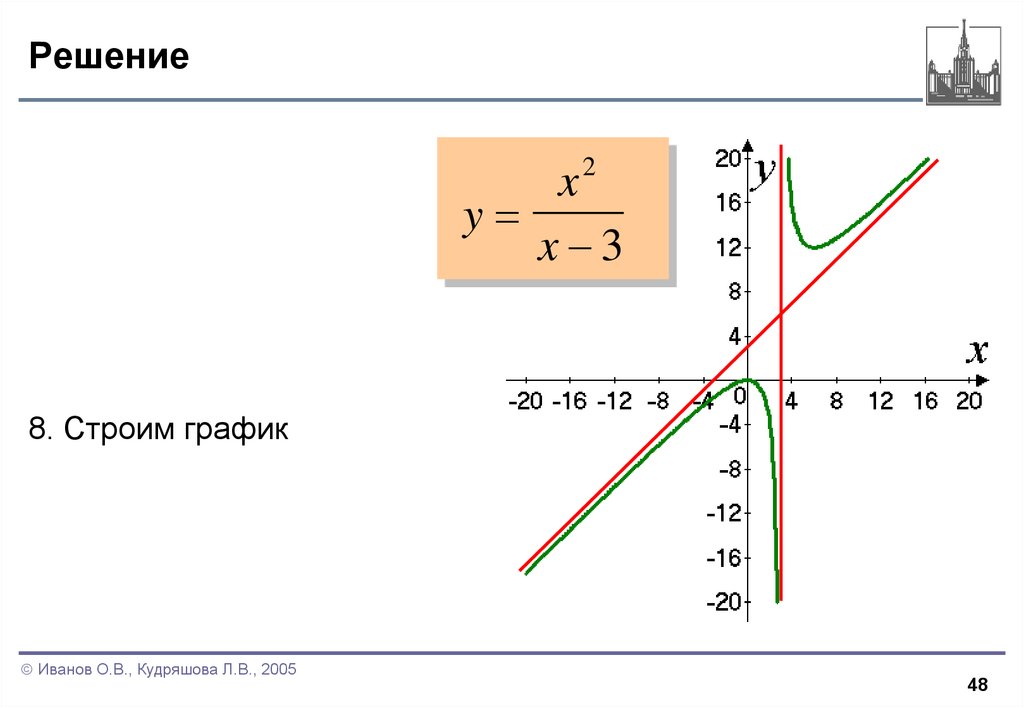
48. Решение
2x
y
x 3
8. Строим график
Иванов О.В., Кудряшова Л.В., 2005
48
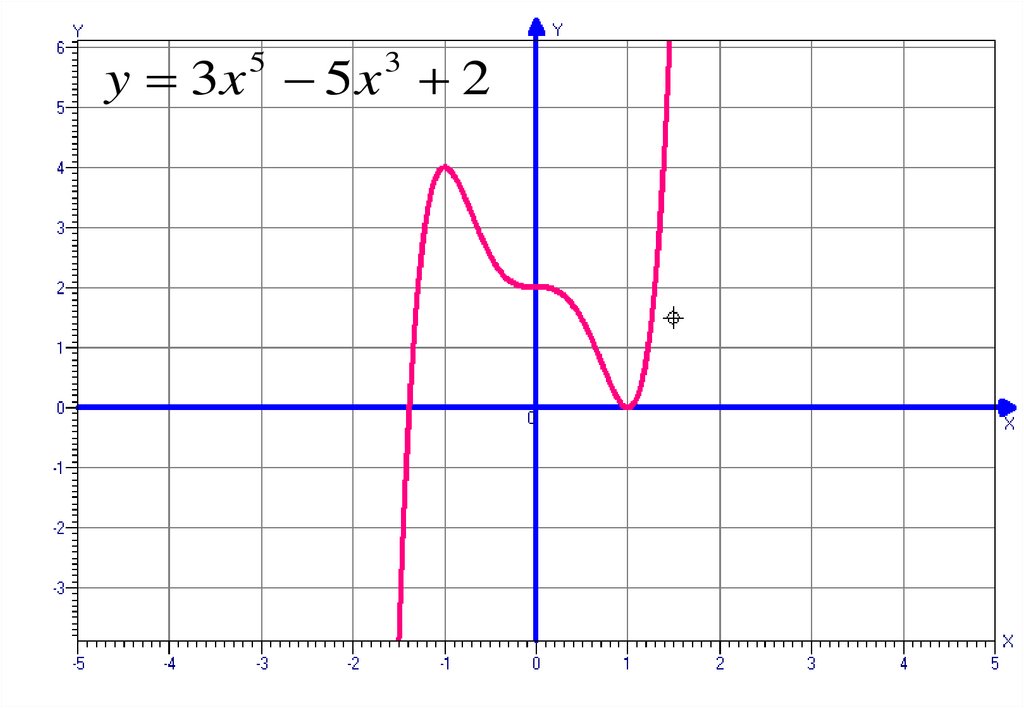
49.
y 5 x 3 3x 5Иванов О.В., Кудряшова Л.В., 2005
49
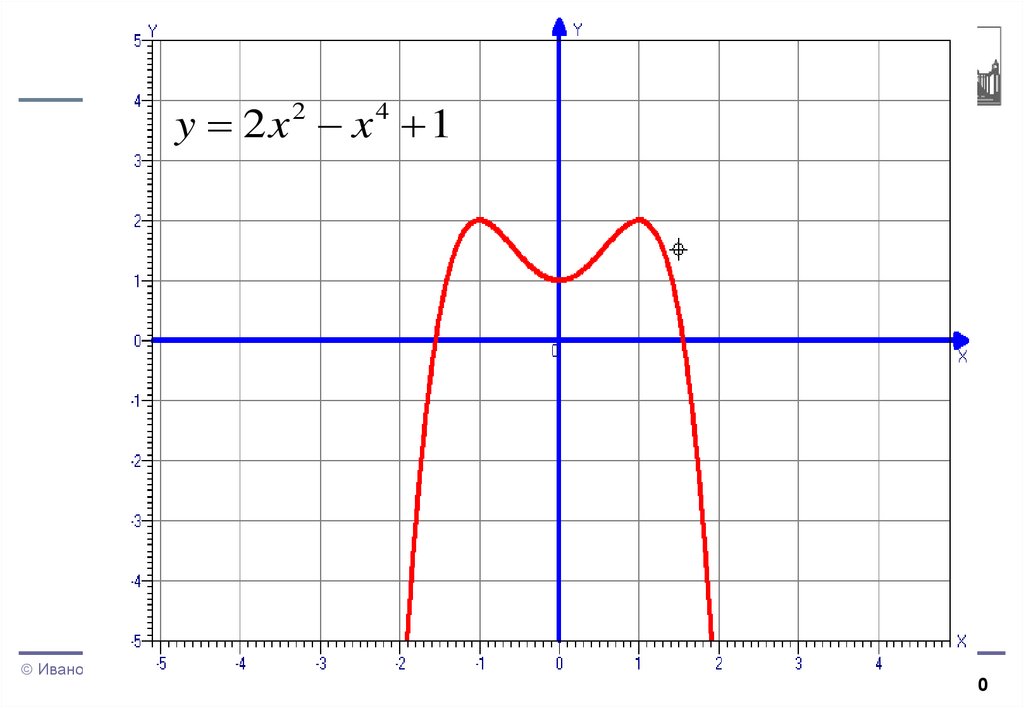
50.
y 2x x 12
Иванов О.В., Кудряшова Л.В., 2005
4
50
51.
y 3x x2
Иванов О.В., Кудряшова Л.В., 2005
3
51
52.
y 3x 5 x 25
Иванов О.В., Кудряшова Л.В., 2005
3
52
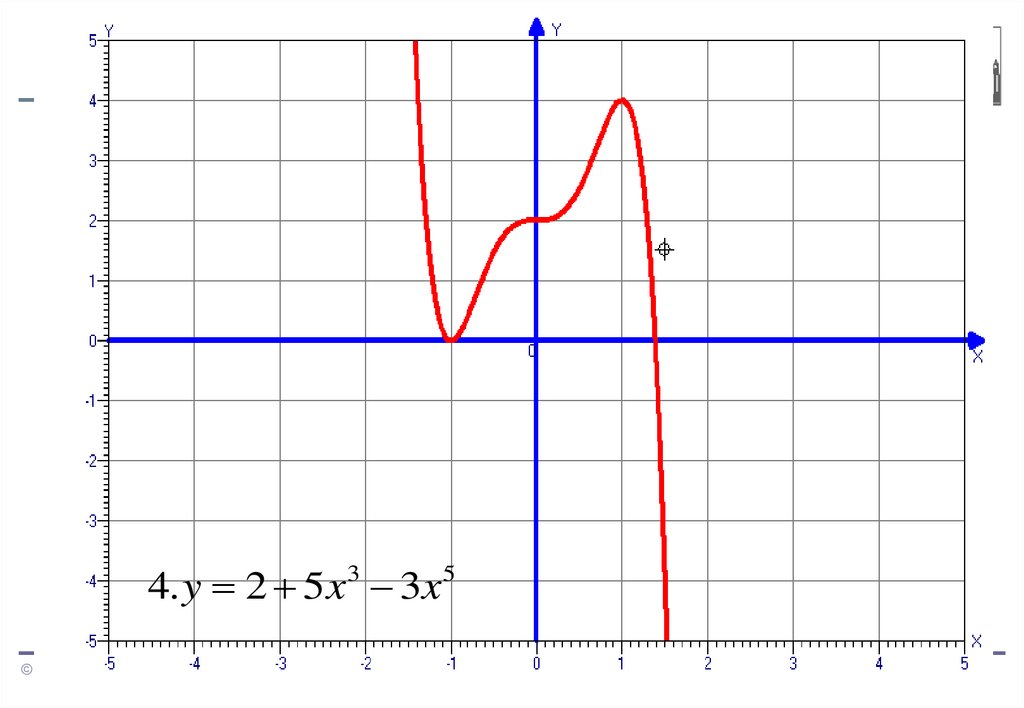
53.
4. y 2 5 x3 3x 5Иванов О.В., Кудряшова Л.В., 2005
53
54.
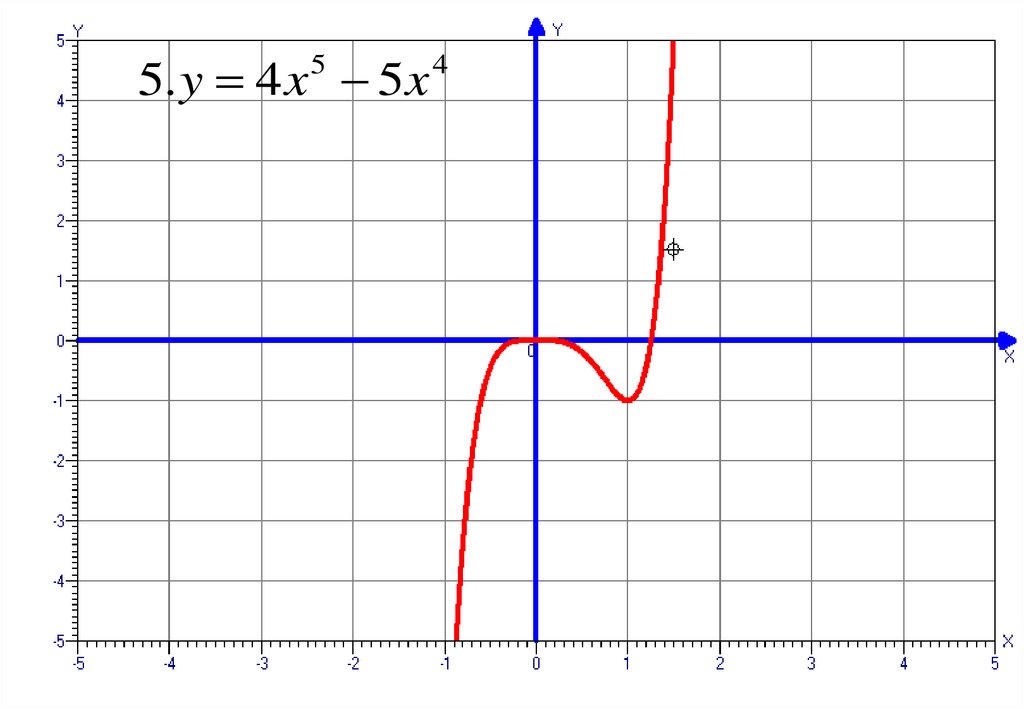
5. y 4 x 5 x5
Иванов О.В., Кудряшова Л.В., 2005
4
54
55.
2xy
2
1 x
Иванов О.В., Кудряшова Л.В., 2005
55
56.
5y
x 10
Иванов О.В., Кудряшова Л.В., 2005
56
57.
1y 2x 2
x
Иванов О.В., Кудряшова Л.В., 2005
57
58.
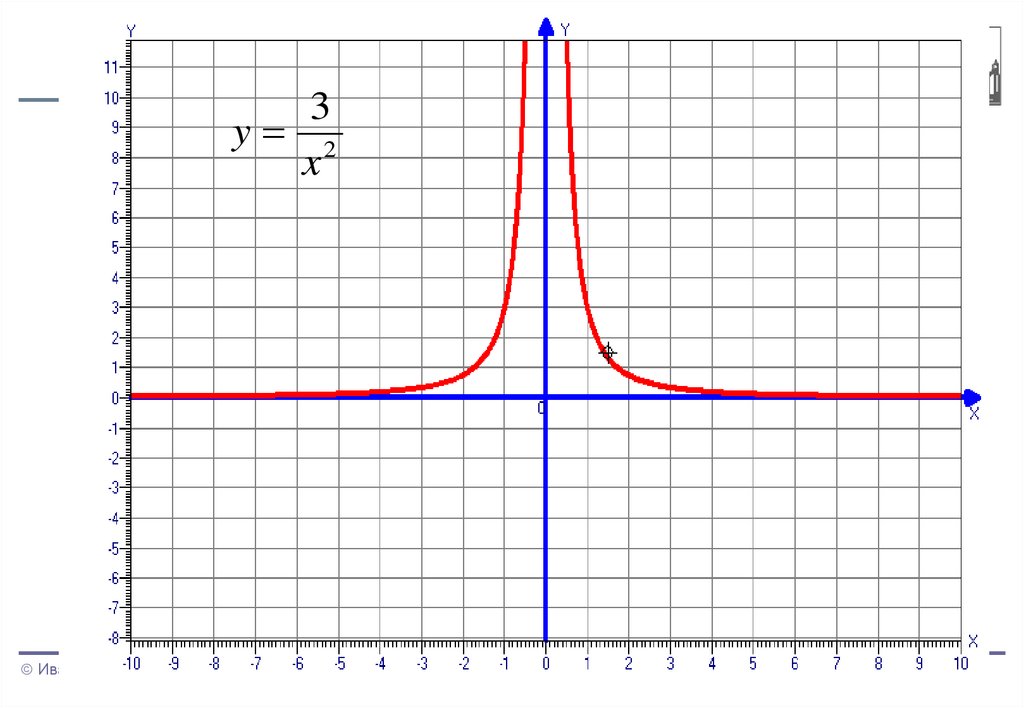
3y 2
x
Иванов О.В., Кудряшова Л.В., 2005
58
59. Новое лекарство. Врачи в клиниках
Будон Р. Место беспорядка. Критика теории социального изменения.1998.
Исследование процесса диффузии фармакологических новинок проведенное
Колеманом и его сотрудниками, выявило одно интересное обстоятельство.
Если рассматривать группу врачей работающих в больницах, то можно
обнаружить, что процесс диффузии принимает специфический характер.
Вначале он весьма неспешен - число медиков, воспринявших новацию,
растет медленно. С течением времени процесс ускоряется - число
«обращенных» возрастает все более и более высокими темпами. Скорость
процесса достигает максимума в тот момент, когда уже примерно половина
медиков стала сторонниками новинки. Начиная с этого момента темп
процесса последовательно замедляется с тем, чтобы полностью сойти на нет
к тому времени, когда почти все сообщество превратится в сторонников
новшества ...
Ссылка: Coleman J., Katz E., Menzel H. Medical Innovation. Diffusion Study. N.Y. 1996.
Иванов О.В., Кудряшова Л.В., 2005
59
60. Новое лекарство. Частные врачи
Будон Р. Место беспорядка. Критика теории социального изменения.1998.
… эта структура, характерная для врачей, работающих в больницах,
неприменима к их коллегам, занятым частной практикой на дому. В
последнем случае число принимающих новацию специалистов резко
возрастает в самом начале. Затем скорость, с которой новация находит
новых сторонников, начинает монотонно снижаться. Скорость все более и
более падает по мере того, как новые врачи становятся сторонниками
новинки, и, наконец, падает до нуля, когда почти все станут таковыми. Если
представить этот процесс в декартовой системе координат, отмечая
временные интервалы на оси абсцисс, а численность сторонников новинки в
каждый последующий момент времени — на оси ординат, то получим фигуру,
напоминающую уже не 8-образную линию, а вытянутую в форме дуги.
Иванов О.В., Кудряшова Л.В., 2005
60
61. Формулы кривых
Кривая насыщения:S (t ) A0 e
или
t
S (t ) A0 1 / t
Логистическая кривая:
t
S (t ) A0 / (1 e )
Обе кривые часто используются для
моделирования социокультурных процессов.
Иванов О.В., Кудряшова Л.В., 2005
описания
или
61















































 Математика
Математика








