Похожие презентации:
Построение графиков функций и уравнений, содержащих модули
1. «Построение графиков функций и уравнений, содержащих модули.»
Г.П.Байло2021 г.
2. Литература:
И.И. Гайдуков «Абсолютная величина»Просвещение, 1968 г.
Ю.Н. Макарычев, Н.Г. Миндюк
«Дополнительные главы к школьному
учебнику»
Просвещение, 2019 г.
3. АБСОЛЮТНАЯ ВЕЛИЧИНА
a, если а > 0,|a|= 0, если а = 0,
-а, если а < 0.
Примеры: 1. |8| = 8
2. |-8| = 8
4. y = f|x|
|x| = |-x|f|-x| = f|x|
y = f|x| - чётная и
график симметричен относительно оси Oy.
5. y = 1/4x2 - |x| - 3
21/4x -
y=
|x| - 3
y
Y
y = 1/4x2 - |x| - 3
16
13
10
7
y = 1/4x2 - x - 3 y = 1/4x2 + x - 3
4
-11
-7
-3
O
1
1
5
9
13
17
21
25
29
33
X
o
x
-2
-5
-8
6. y = 1/2|x|+1/2
yY
y = 1/2|x| + 1/2
16
13
10
7
y = 1/2x + 1/2 y = -1/2x + 1/2
4
-11
-7
-3
O
1
1
5
9
13
17
21
25
29
33
X
o
x
-2
-5
-8
7. y = |f(x)|
f(x), где f(x) > = 0,y=
-f(x),где f(x) < 0.
8. y = |x2 – x – 6|
y=Y
2
|x
– x – 6|
Построение:
y
16
а) График y = x2 -x – 6 .
13
б) Участок графика ,
где y<0, отображаем
симметрично
относительно оси Ox.
10
7
4
-11
-7
-3
O
1
1
o
5
9
13
x
-2
-5
17
21
25
29
9. y = |f|x||
Правило построения:а)Строим график функции y = f|x|.
б) Участки графика , где y<0,
отображаем симметрично
относительно оси Ox.
10. y = |2|x| - 3|
yПостроение:
Y
а) График y = 2x – 3 для x>0.
б) График y = -2x – 3 для x<0.
в) Кривые симметричные
относительно оси Ox для
f(x)<0.
16
13
10
7
4
-11
-7
-3
O
1
1
5
9
13
17
21
25
29
33
X
o
x
-2
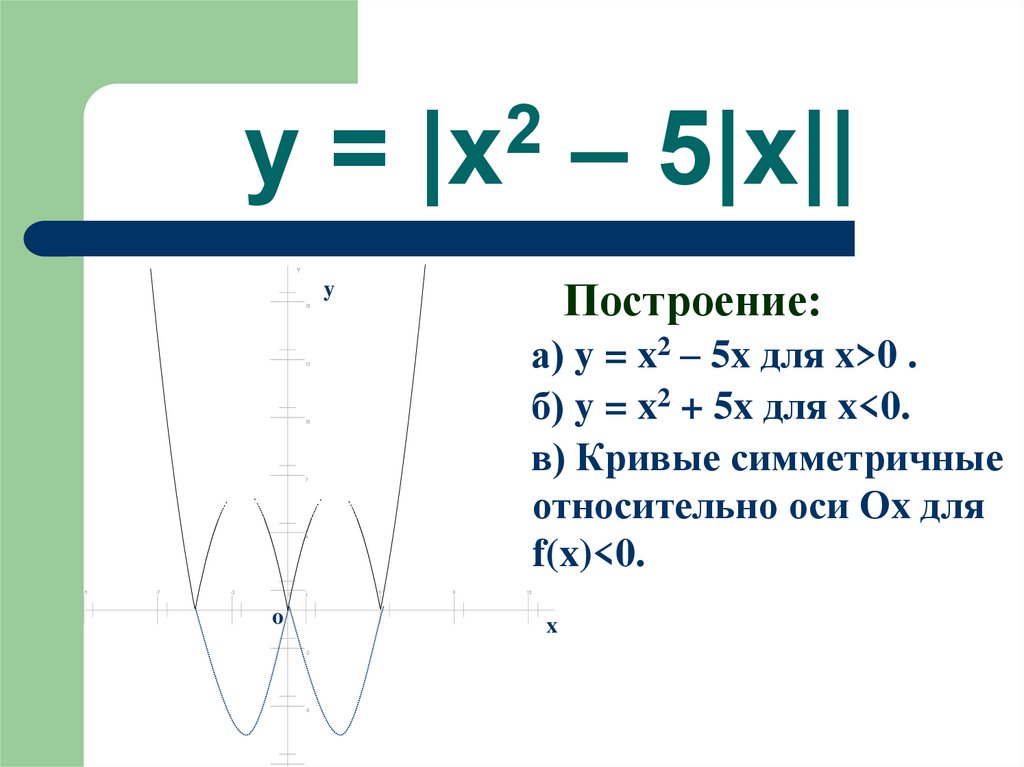
11. y = |x2 – 5|x||
y=– 5|x||
2
|x
y
Y
Построение:
y
16
а) y = x2 – 5x для x>0 .
б) y = x2 + 5x для x<0.
в) Кривые симметричные
относительно оси Ox для
f(x)<0.
13
10
7
4
-11
-7
-3
O
1
1
5
9
13
17
21
25
29
33
X
o
x
-2
-5
12. |y| = f(x), где f(x) >= 0
|y| = f(x), где f(x) >= 0y = +-f(x), где f(x) > = 0
График симметричен относительно оси Ox
13. Правило построения:
а) Установить область определенияфункции из условия: f(x)> =0.
б) Построить y = f(x).
в) Построить кривые симметричные y = f(x)
относительно оси Ox.
14. |y| = 1/2x + 1
Построение:Y
а) Область определения
для 1/2x + 1> =0
x> = -2 .
б) График y = 1/2x +1,
для x> = -2.
y
16
13
10
7
4
-11
-7
-3
O
1
1
5
9
13
17
21
25
29
33
X
-2
o
x
-2
-5
-8
-11
в) Кривая симметричная
Ox.
15. |y| = |f(x)|
y = +-|f(x)|график симметричен относительно
осей Ox и Oy.
Правило построения:
а) y = |f(x)| (весь в верхней полуплоскости).
б) y = -|f(x)| (кривая симметричная y = |f(x)|).
16. |y| = |x2 – 2x|
– 2x|2
|x
|y| =
y
Y
Построение:
16
13
а) y = |x2 – 2x| для y>0
б) y = -|x2 – 2x| для y<0
10
7
4
-11
-7
-3
O
1
1
5
9
13
17
21
25
29
33
X
x
-2
-5
-8
-11
-14
17. |y| + |x| = a
a>=0|x|<=a и |y|<=a, т. е. Д(f): -a<= x <=a
и E(f): –a <= y <=a
т. к. |-y|=|y| и |-x|=|x| график симметричен
относительно осей координат.
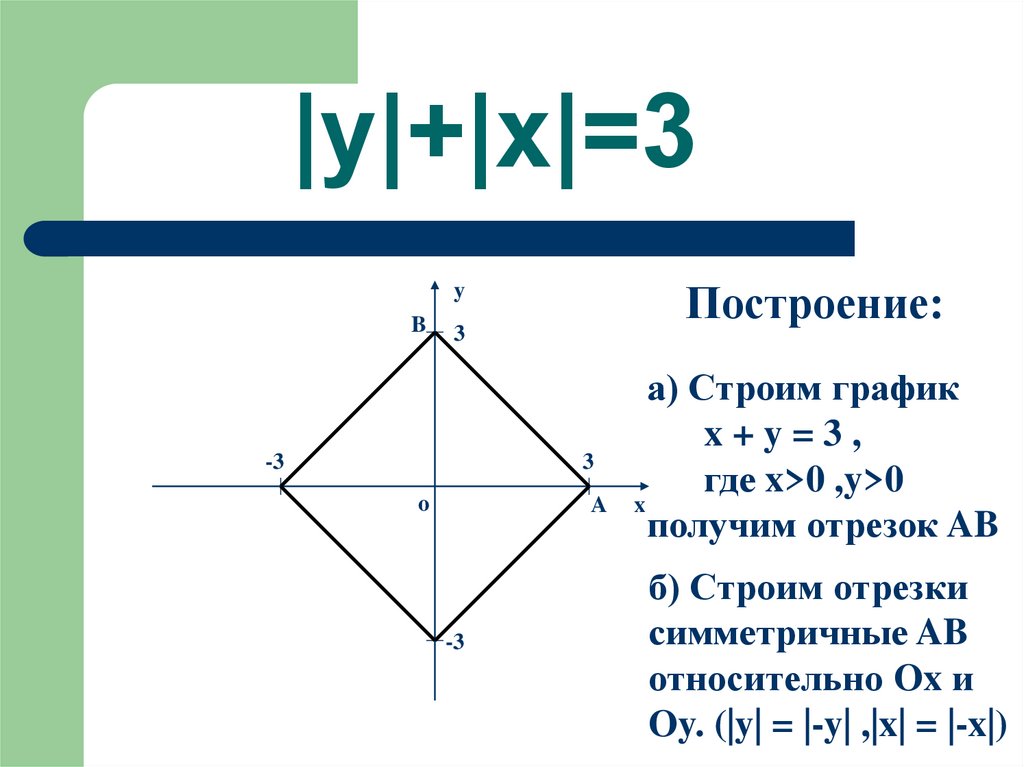
18. |y|+|x|=3
Построение:y
B
3
-3
3
o
A
-3
а) Строим график
x+y=3,
где x>0 ,y>0
x
получим отрезок AB
б) Строим отрезки
симметричные AB
относительно Ox и
Oy. (|y| = |-y| ,|x| = |-x|)






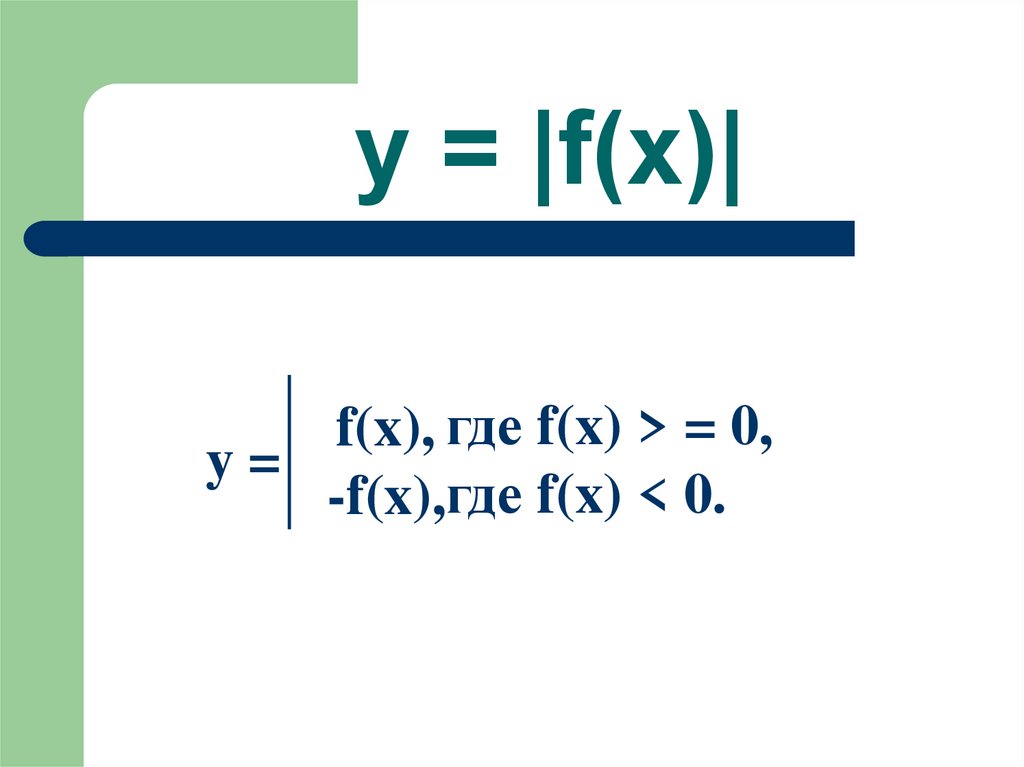









 Математика
Математика








