Похожие презентации:
Параллельные прямые. Исторический отдел
1.
В геометрии истинность каждогоутверждения необходимо доказывать,
нельзя полагаться только на
наблюдения
2.
Параллельные прямыеЦель:
● Познакомиться с различными способами
построения параллельных прямых;
● Научиться строить параллельные прямые.
3.
4.
Исторический отделГреческое слово «параллелой»
означает «рядом идущее», «друг подле
друга проведенные». Стало
употребляться как геометрический
термин еще 2500 лет назад в школе
Пифагора. В «Началах» Евклида учения
о параллельных излагается в одной из
его 13 книг. Символ «параллельности»
известен с античных времён, его
использовали Герон и Папп
Александрийский. Сначала символ
был похож на нынешний знак
равенства, но с появлением
последнего, во избежание путаницы,
символ был повёрнут вертикально.
Евкли́д — древнегреческий
математик, геометр, автор
первого из дошедших до нас
теоретических трактатов по
математике.
5.
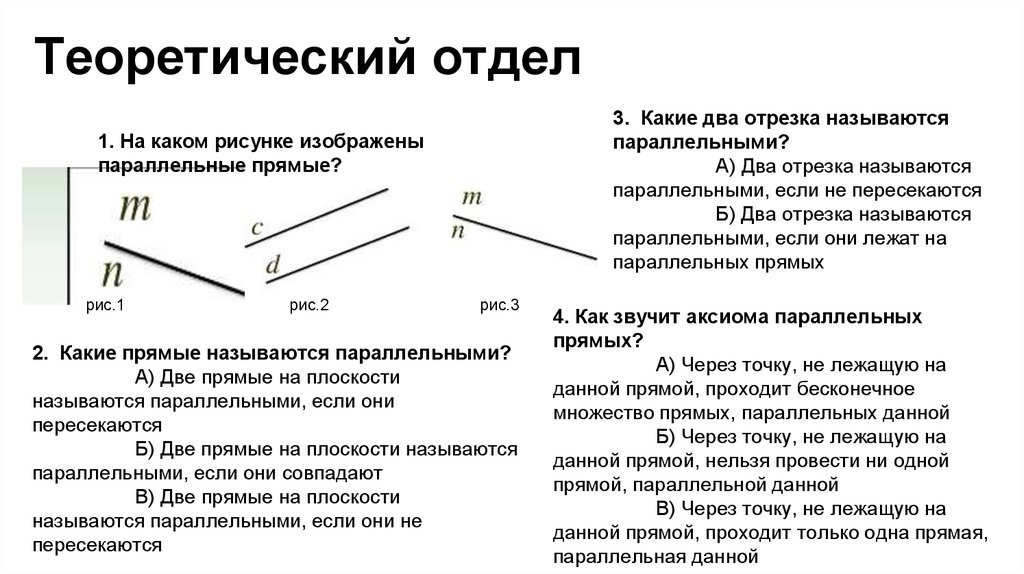
Теоретический отдел3. Какие два отрезка называются
параллельными?
А) Два отрезка называются
параллельными, если не пересекаются
Б) Два отрезка называются
параллельными, если они лежат на
параллельных прямых
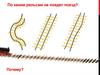
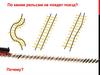
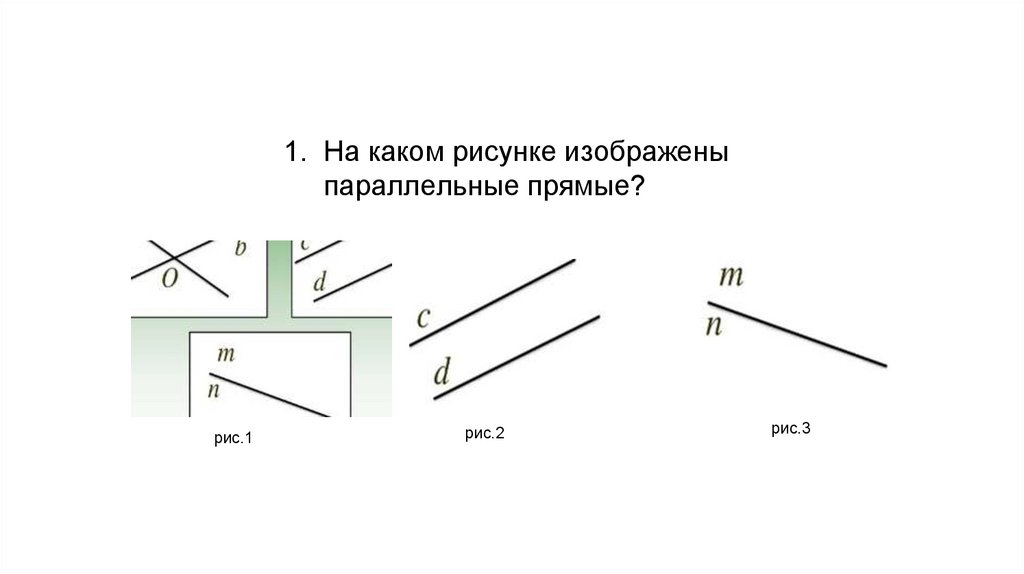
1. На каком рисунке изображены
параллельные прямые?
рис.1
рис.2
рис.3
2. Какие прямые называются параллельными?
А) Две прямые на плоскости
называются параллельными, если они
пересекаются
Б) Две прямые на плоскости называются
параллельными, если они совпадают
В) Две прямые на плоскости
называются параллельными, если они не
пересекаются
4. Как звучит аксиома параллельных
прямых?
А) Через точку, не лежащую на
данной прямой, проходит бесконечное
множество прямых, параллельных данной
Б) Через точку, не лежащую на
данной прямой, нельзя провести ни одной
прямой, параллельной данной
В) Через точку, не лежащую на
данной прямой, проходит только одна прямая,
параллельная данной
6.
1. На каком рисунке изображеныпараллельные прямые?
рис.1
рис.2
рис.3
7.
2. Какие прямые называются параллельными?А) Две прямые на плоскости называются
параллельными, если они пересекаются
Б) Две прямые на плоскости называются
параллельными, если они совпадают
В) Две прямые на плоскости называются
параллельными, если они не пересекаются
8.
3. Какие два отрезка называются параллельными?А) Два отрезка называются параллельными, если
не пересекаются
Б) Два отрезка называются параллельными, если
они лежат на параллельных прямых
9.
4. Как звучит аксиома параллельных прямых?А) Через точку, не лежащую на данной прямой, проходит
бесконечное множество прямых, параллельных данной
Б) Через точку, не лежащую на данной прямой, нельзя провести
ни одной прямой, параллельной данной
В) Через точку, не лежащую на данной прямой, проходит только
одна прямая, параллельная данной
10.
4 верных ответа – оценка «5»3 верных ответа – оценка «4»
2 верных ответа – оценка «3»
Меньше 2 верных ответа – оценка «2»
11.
Отдел исследований12.
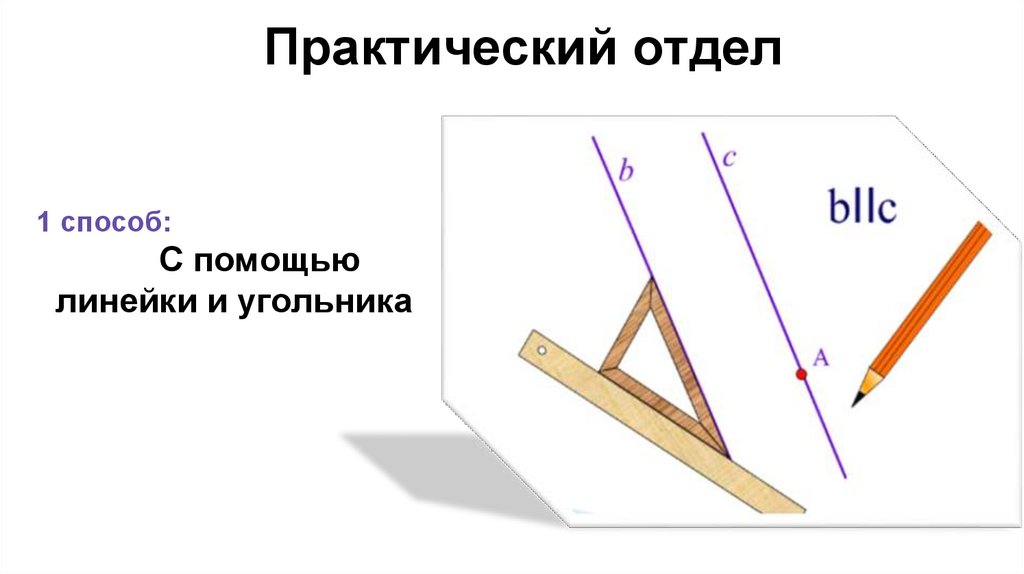
Практический отдел1 способ:
С помощью
линейки и угольника
13.
Практическая работаЗадание: через точку А провести
прямую параллельную прямой с.
с
В
а
А
14.
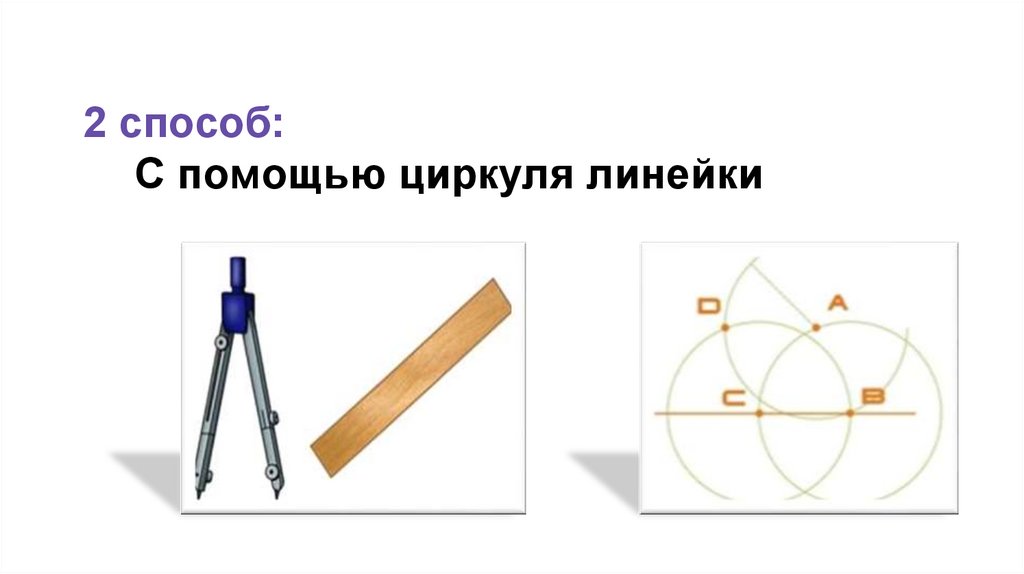
2 способ:С помощью циркуля линейки
15.
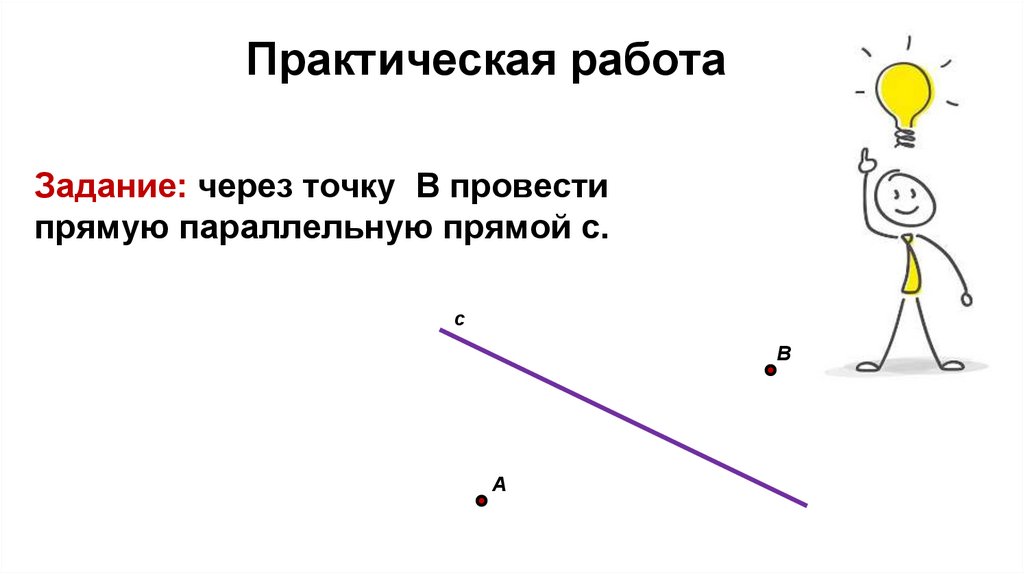
Практическая работаЗадание: через точку В провести
прямую параллельную прямой с.
с
В
А
16.
Алгоритм построения с помощью циркуля илинейки:
1. Выберем произвольную точку на данной прямой и назовем ее C.
2. С помощью циркуля начертим окружность радиуса ВC с центром в точке C.
3. На пересечении окружности и прямой отметим точку и назовем ее E.
4. С тем же радиусом ВC построим окружность с центром в точке E.
5. С прежним радиусом BC построим третью окружность с центром в точке B.
6. Отметим точку пересечения второй и третьей построенных окружностей
и назовем ее O.
7. Через точки B и О проведем прямую, которая будет параллельной заданной.
17.
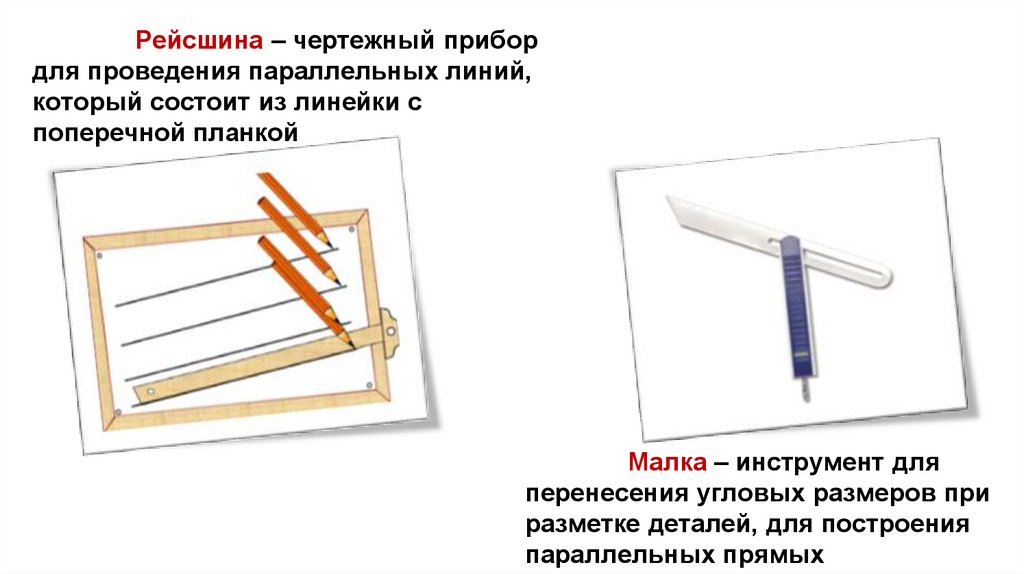
Рейсшина – чертежный прибордля проведения параллельных линий,
который состоит из линейки с
поперечной планкой
Малка – инструмент для
перенесения угловых размеров при
разметке деталей, для построения
параллельных прямых
18.
Теорема: Две прямые, параллельные третьей,параллельны
а
b
с
А
a║c
ቋ =>a ║ b
b║c
В
19.
Доказательство:а
с
b
а
О
с
Аксиома: Через точку,
не лежащую на данной прямой
можно провести только одну
прямую, параллельную данной
b













 Математика
Математика