Параллельные прямые

1.

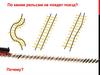
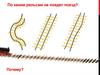
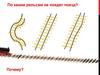
По каким рельсам не поедет поезд?
Почему?

2. Параллельные прямые.

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ.
ПЛАН:
1. Какие две прямые называют параллельными?
2. Каким символом обозначают параллельность
прямых?
3. Как читают запись m║n?
4. Какие отрезки называют параллельными?
5. Каково взаимное расположение двух прямых,
перпендикулярных третьей прямой?
6. Сформулируйте аксиому параллельности прямых.
7. Каково взаимное расположение двух прямых,
параллельных третьей прямой?
8.
Если прямая пересекает одну из двух параллельных
прямых, то как эта прямая расположена
относительно второй из параллельных Прямых?
9. Построение параллельных прямых.
10. Решение задач.

3. Параллельные прямые

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Продолжите предложения:
Прямые, имеющие одну общую точку - ……………………
Какие две прямые называют
Прямые, не имеющие
параллельными?
общих точек - ……………………
Прямые, имеющие две общие точки - ……………………

4.

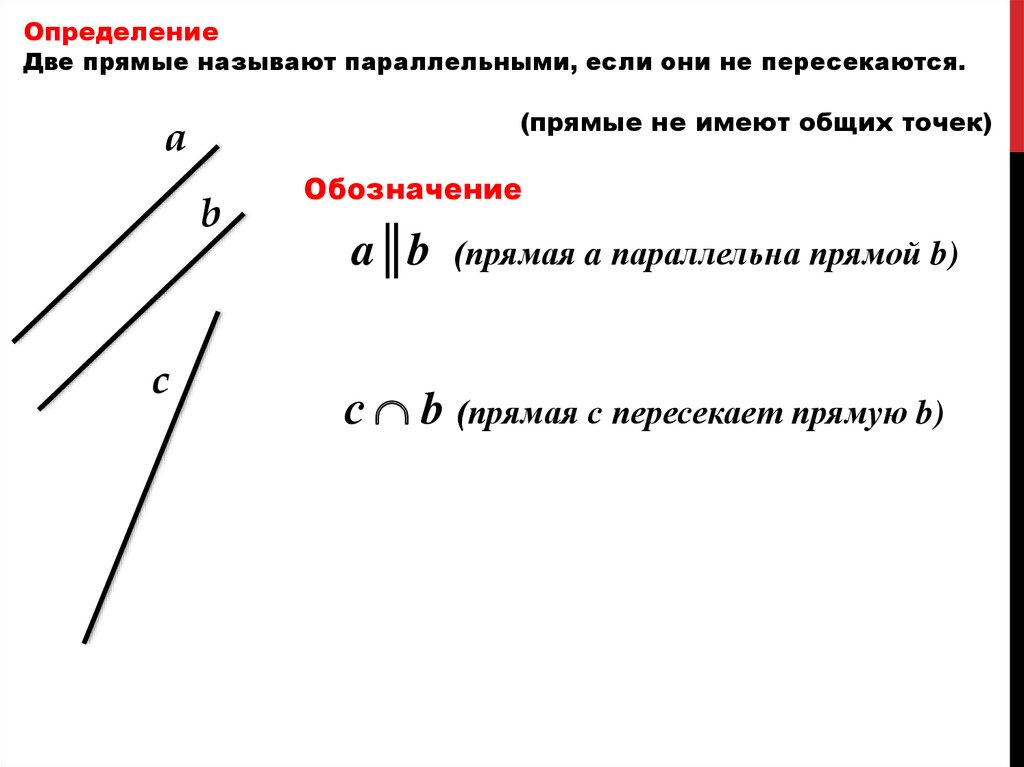
Определение
Две прямые называют параллельными, если они не пересекаются.
(прямые не имеют общих точек)
a
b
c
Обозначение
a║b
(прямая a параллельна прямой b)
с b (прямая с пересекает прямую b)

5.

Определение
Две прямые называют параллельными, если они не пересекаются.
a
В
D
А
a
b
a║b,
b
АВ║CD
А
Какие
отрезки (лучи)называют
C
C
параллельными?
N
M
c
d
K
с d, не MN║KP
N
P
M
c
d
K
P

6.

Определение
Две прямые называют параллельными, если они не пересекаются.
a
a b, b c
b
c
a║b
Теорема 13.1
(признак параллельности прямых)
Каково взаимное
Две прямые, перпендикулярные
расположение
двух прямых,
третьей прямой, параллельны.
перпендикулярных
третьей
Предположим, что прямые a b в
точке М.
М
прямой?
Но тогда через точку не лежащую на
a
b
c
прямой проходят две прямые
перпендикулярные данной прямой с ,
сто противоречит свойству
перпендикулярных прямых, а это
значит, что предположение неверное
и эти прямые не пересекаются, а
значит параллельны.

7.

Две прямые, перпендикулярные к третьей, параллельны.
Найди на чертежах параллельные прямые a и b
и щелкни по ним мышкой.
2
1
ВЕРНО!!!
3
а
а
а
b
b
b
4
5
6
а
b
а
b
b
НЕ ВЕРНО!!!

8.

Следствие
Через данную точку М, не принадлежащую
прямой а, можно провести прямую b,
параллельную прямой а.
М
b
a
с
Доказательство
Пусть точка М не принадлежит прямой а
Проведём (например, с помощью
угольника) через точку М прямую c
перпендикулярную прямой а. Теперь
через точку М проведём прямую b,
перпендикулярную прямой с. В силу
теоремы 13.1 а ║ b.
Сколько прямых можно провести через
точку М, параллельно прямой а?

9.

Построение прямой, параллельной
данной
Алгоритм.
1. Наложите угольник на данную
прямую так, чтобы одна из
сторон прямого угла (катет
прямоугольного треугольника)
совпала с данной прямой.
2. Приложите ко второй стороне
прямого угла (катету
прямоугольного треугольника)
линейку.
3. Передвиньте угольник по
линейке (как по рельсам)
4. Вдоль стороны, которая до
переноса совпадала с прямой,
к которой нужно провести
параллельную прямую
проведите линию.
5. Данная прямая будет
параллельной к данной прямой.

10.

Определение
Две прямые называют параллельными, если они не пересекаются.
М
b
Основное свойство
параллельных прямых
(аксиома параллельности
прямых)
Через точку, не
Сформулируйте
аксиому
лежащую
на данной
a
прямой,
проходит
параллельности
прямых.
только одна прямая,
с
параллельная данной.

11.

Две прямые, перпендикулярные к третьей, параллельны.
b
c
А
bIIc
a

12.

Определение
Две прямые называют параллельными, если они не пересекаются.
Теорема 13.2
a
b
cКаково
Если две прямые
параллельны третьей
прямой, то они параллельны.
взаимное
расположение двух прямых,
Доказательство
параллельных
третьей
прямой?
Пусть b II c и a II c. Докажем, что b II a.
Предположим, что прямые а и b не параллельны, а
пересекаются в некоторой точке М.
Получается, что через точку М проходят две прямые,
параллельные прямой c, что противоречит аксиоме
параллельности прямых. Следовательно, b || a.

13.

Определение
Две прямые называют параллельными, если они не пересекаются.
b
a
M
c
Задача. Докажите, что если прямая
пересекает одну из двух
параллельных прямых,
то она пересекает и другую.
Решение.
Пусть прямые а и b параллельны, прямая с пересекает
прямую b в точке М.
Предположим, что прямая с не пересекает прямую а,
тогда с II а.
Но в этом случае через точку М проходят две прямые,
параллельные прямой а, что противоречит аксиоме
параллельности прямых.
Следовательно, прямая с пересекает прямую а.

14. Параллельные прямые.

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ.
ПЛАН:
1. Какие две прямые называют параллельными?
2. Каким символом обозначают параллельность
прямых?
3. Как читают запись m║n?
4. Какие отрезки называют параллельными?
5. Каково взаимное расположение двух прямых,
перпендикулярных третьей прямой?
6. Сформулируйте аксиому параллельности прямых.
7. Каково взаимное расположение двух прямых,
параллельных третьей прямой?
8.
Если прямая пересекает одну из двух параллельных
прямых, то как эта прямая расположена
относительно второй из параллельных Прямых?
9. Построение параллельных прямых.
10. Решение задач.

15. Практические задания Стр. 86 учебника , № 285, 286.

ПРАКТИЧЕСКИЕ ЗАДАНИЯ
СТР. 86 УЧЕБНИКА , № 285, 286.

16. Работа в парах Стр. 87 учебника, № 288, 290, 291, 293

РАБОТА В ПАРАХ
СТР. 87 УЧЕБНИКА, № 288, 290, 291, 293
Алгоритм учебного исследования
1. Прочитайте задачу.
2. Сделайте чертёж.
3. Определите, какой геометрический факт (определение
параллельных прямых или их свойства) вам помогут
дать ответ на поставленный вопрос.
4. Запишите краткий ответ с помощью математических
обозначений

17. Д. з. Всем выучить определение и теоремы с доказательством БУ: № 287, 289, 292, ПУ: №294, УУ: № 299

Д. З. ВСЕМ ВЫУЧИТЬ ОПРЕДЕЛЕНИЕ
И ТЕОРЕМЫ С ДОКАЗАТЕЛЬСТВОМ
БУ: № 287, 289, 292,
ПУ: №294,
УУ: № 299