Похожие презентации:
Теорема Пифагора. Урок геометрии
1. Урок геометрии на тему : «Теорема Пифагора»
Работу выполнила:учитель математики
МБОУ СОШ №28
Копылова
Ирина Викторовна.
2. Добро пожаловать на урок геометрии !
Добро пожаловатьна урок геометрии
!Суть истины вся в том, что
нам она- навечно,
когда хоть раз в прозрении
её увидим свет,
и теорема Пифагора через
столько лет
для нас. Как для него,
бесспорна, безупречна.
А.Шамиссо
3. Содержание
10.Цели урока.(слайд 4)
Систематизация знаний.(слайд 5)
Биография Пифагора.(слайд 6)
История теоремы Пифагора.(слайд 7)
Теорема Пифагора(слайд 8)
Доказательство теоремы(слайд 9)
Решите задачи.(слайд 10)
Самопроверяющая самостоятельная работа.(слайд
11)
Проверь себя.(слайд 12)
Исторические задачи.(слайды13-14)
11.
Домашнее задание.(слайд15)
1.
2.
3.
4.
5.
6.
7.
8.
9.
4. Цели урока:
Обучающая :систематизировать знания по теме «Теорема
Пифагора»
научить решать задачи по данной теме.
Воспитательная:
воспитывать любовь к математике, готовность к
труду , дисциплинированность.
Развивающая :
развитие логического мышления, воли,
самостоятельности мышления в учебной
деятельности.
5. Систематизация знаний :
1.2.
3.
4.
Биография Пифагора
История теоремы Пифагора
Теорема Пифагора
Доказательство теоремы Пифагора
6. Биография Пифагора
О жизни Пифагора известно немного в Древней Греции на острове Самос, который находится вЭгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским.
Родился Пифагор в семье резчика по камню, который сыскал скорее славу, чем богатство. Ещё
в детстве он проявлял незаурядные способности, и когда подрос, неугомонному воображению
юноши стало тесно на маленьком острове.
Пифагор перебрался в город Милеет и стал учеником Фалеса, которому. Он родился в 580 г . до
н.э то время шёл восьмой дес. в яток. Мудрый учёный посоветовал юноше отправиться в
Египет, где сам, когда-то изучал науки.
Перед Пифагором открылась неизвестная страна. Его поразило то, что в родной Греции боги
были в образе людей, а египетские боги – в образе полулюдей-полуживотных. Знания были
сосредоточены в храмах, доступ в которые был ограничен. Пифагору потребовались годы,
чтобы глубоко изучить египетскую культуру прежде, чем, ему было разрешено познакомиться с
многовековыми достижениями египетской науки.
Когда Пифагор постиг науку египетских жрецов, то засобирался домой, чтобы там создать свою
школу. Жрецы, не желавшие распространения своих знаний за пределы храмов, не хотели его
отпускать. С большим трудом ему удалось преодолеть эту преграду.
Однако по дороге домой, Пифагор попал в плен и оказался в Вавилоне. Вавилоняне ценили
умных людей, поэтому он нашёл своё место среди вавилонских мудрецов. Наука Вавилона была
более развитой, нежели египетская. Наиболее поразительными были успехи алгебры.
Вавилоняне изобрели и применяли при сёте позиционную систему счисления, умели решать
линейные, квадратные и некоторые виды кубических уравнений.
Пифагор прожил в Вавилоне около десяти лет и в сорокалетнем возрасте вернулся на родину.
Но на острове Самос он оставался недолго. В знак протеста против тирана Поликрата, который
тогда правил островом, поселился в одной из греческих колоний Южной Италии в городе
Кротоне.
Там Пифагор организовал тайный союз молодёжи из представителей аристократии. В этот союз
принимались с большими церемониями после долгих испытаний. Каждый вступающий
отрекался от своего имущества и давал клятву хранить в тайне учения основателя.
Пифагорейцы, как их позднее стали называть, занимались математикой, философией,
естественными науками. В школе существовал декрет, по которому авторство всех
математических работ приписывалось учителю
7. История теоремы Пифагора
Хотя эта теорема и связана сименем Пифагора, она была
известна задолго до него. В
вавилонских текстах эта
теорема встречается за 1200
лет до Пифагора. Соотношение
между гипотенузой и катетами
было установлено опытным
путем на основе измерений.
Пифагор нашел доказательство
этого соотношения. На
протяжении последующих веков
были найдены различные
другие доказательства теоремы
Пифагора. В настоящее время
их насчитывается более ста.
8. Теорема Пифагора
В прямоугольном треугольнике квадратгипотенузы равен сумме квадратов
катетов.
в
с
а
а +в =с
2
2
2
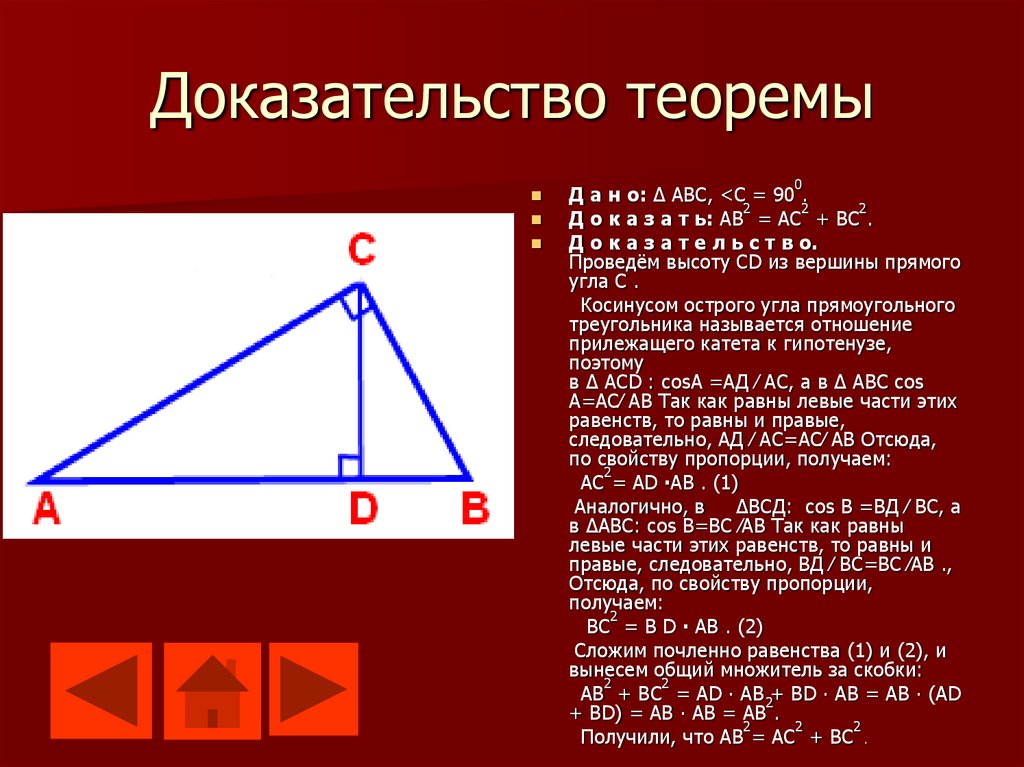
9. Доказательство теоремы
0Д а н о: ∆ АВС, <С = 90 .
2
2
2
Д о к а з а т ь: АВ = АС + ВС .
Д о к а з а т е л ь с т в о.
Проведём высоту CD из вершины прямого
угла С .
Косинусом острого угла прямоугольного
треугольника называется отношение
прилежащего катета к гипотенузе,
поэтому
в ∆ ACD : cosА =АД ∕ АС, а в ∆ АВС cos
А=АС∕ АВ Так как равны левые части этих
равенств, то равны и правые,
следовательно, АД ∕ АС=АС∕ АВ Отсюда,
по свойству пропорции, получаем:
2
АС = AD ∙АВ . (1)
Аналогично, в
∆ВСД: cos В =ВД ∕ ВС, а
в ∆АВС: cos В=ВС ∕АВ Так как равны
левые части этих равенств, то равны и
правые, следовательно, ВД ∕ ВС=ВС ∕АВ .,
Отсюда, по свойству пропорции,
получаем:
2
ВС = В D ∙ АВ . (2)
Сложим почленно равенства (1) и (2), и
вынесем общий множитель за скобки:
2
2
АВ + ВС = AD ∙ AB 2+ BD ∙ AB = AB ∙ (AD
+ BD) = AB ∙ AB = AB .
2
2
2
Получили, что АВ = АС + ВС .
10. Решите задачи:
В прямоугольном треугольнике а и в- катеты, а сгипотенуза. Найдите в ,если а=12,с=13.В прямоугольнике АВСД найдите АД, если
АВ=5,АС=13.
Боковая сторона равнобедренного треугольника
равна 17 см., а основание равно 16 см. Найдите
высоту, проведенную к основанию.
Найдите площадь трапеции АВСД с основаниями АВ
и СД, если АВ=10 см.,ВС=ДА=13 см.,СД=20см.
11. Самопроверяющая самостоятельная работа Найти неизвестное х: Варианты ответов:
Самопроверяющая самостоятельная работаНайти неизвестное х:
1
Варианты ответов:
2
8
х
а
х
6
2а
3
4
х
√2а
а
8
15
5
300
х
6
х
4
1
х
7
5
√6
д
х
√26
10
√28
ц
м
к
√5
а√3
е
о
6
17
!
л
8
3
1
2
14
х
х
30
0
12. Проверь себя:
мо
л
о
д
е
ц
!
10
а√3
17
а√3
2
√5
√26
6
13. Исторические задачи 1.Задача из учебника «Арифметика» Леонтия Магницкого.
«Случися некому человеку к стене лестницуприбрати, стены же тоя высота есть 117
стоп. И обреете лестницу долготью 125
стоп. И ведати хочет, колико стоп сея
лестницы
нижний
конец
от
стены
отстояти имать».
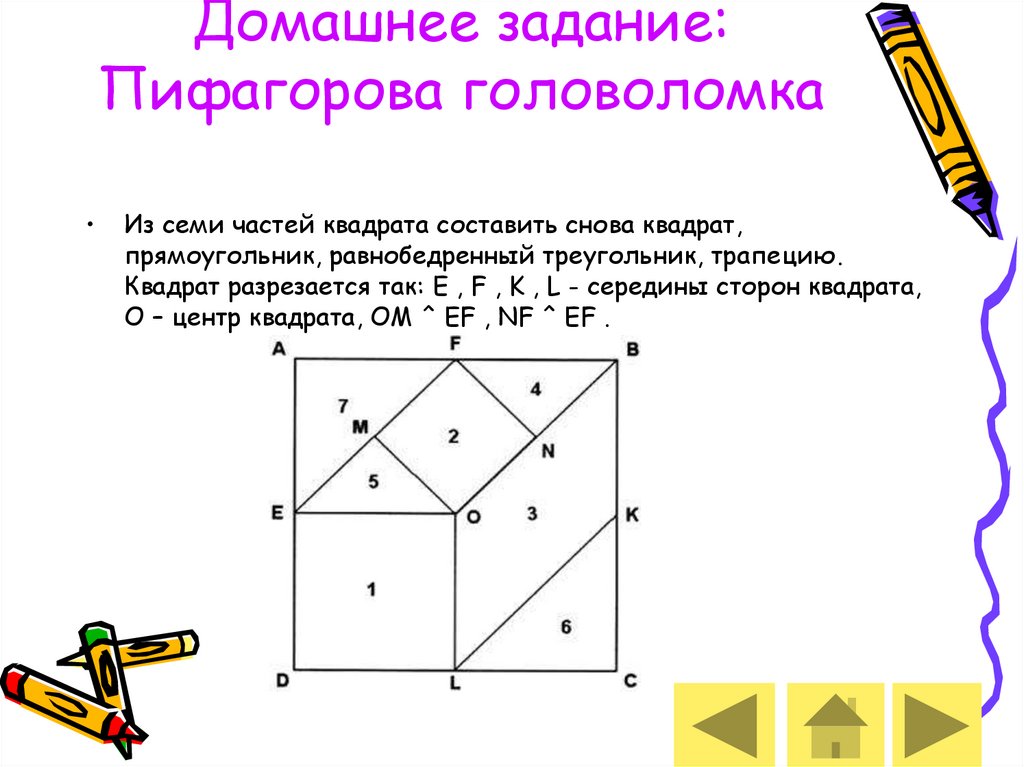
14. Домашнее задание: Пифагорова головоломка
Из семи частей квадрата составить снова квадрат,
прямоугольник, равнобедренный треугольник, трапецию.
Квадрат разрезается так: E , F , K , L - середины сторон квадрата,
О – центр квадрата, ОМ ^ EF , NF ^ EF .
15.
2. Задача из китайской«Математики в девяти книгах»
«Имеется водоем со стороной в 1 чжан = 10 чи.
В центре его растет камыш, который
выступает над водой на 1 чи. Если потянуть
камыш к берегу, то он как раз коснётся его.
Спрашивается: какова глубина воды и какова
длина камыша?».













 Математика
Математика








