Статистическая проверка случайных чисел. Лекция № 2

1.

Лекция № 2
2 критерий Пирсона
λ критерий Колмогорова-Смирнова

2. Назначения критерия

Критерий 2 применяется в двух целях;
1) для сопоставления эмпирического распределения
признака с теоретическим - равномерным,
нормальным или каким-то иным;
2) для сопоставления двух, трех или более
эмпирических распределений одного и того же
признака.

3. Описание критерия

Критерий 2 отвечает на вопрос о том, с одинаковой ли
частотой встречаются разные значения признака в
эмпирическом и теоретическом распределениях или в
двух и более эмпирических распределениях.
Преимущество метода состоит в том, что он позволяет
сопоставлять распределения признаков,
представленных в любой шкале, начиная от шкалы
наименований. В самом простом случае
альтернативного распределения "да - нет", "допустил
брак - не допустил брака", "решил задачу - не решил
задачу" и т. п. мы уже можем применить критерий.

4.

При сопоставлении эмпирического распределения с
теоретически мы определяем степень расхождения
между эмпирическими и теоретическими частотами.
При сопоставлении двух эмпирических распределений
мы определяем степень расхождения между
эмпирическими частотами и теоретическими
частотами, которые наблюдались бы в случае
совпадения двух этих эмпирических распределений.
Формулы расчета теоретических частот будут
специально даны для каждого варианта
сопоставлений.
Чем больше расхождение между двумя
сопоставляемыми распределениями, тем больше
эмпирическое значение 2 .

5.

Гипотезы
Возможны несколько вариантов гипотез, в зависимости
от задачи которые мы перед собой ставим.
Первый вариант:
Н0: Полученное эмпирическое распределение признака
не отличается от теоретического (например,
равномерного) распределения.
Н1: Полученное эмпирическое распределение признака
отличается от теоретического распределения.

6.

Второй вариант:
Н0: Эмпирическое распределение 1 не отличается от
эмпирического распределения 2.
Н1: Эмпирическое распределение 1 отличается от
эмпирического распределения 2.
Третий вариант:
Н0: Эмпирические распределения 1, 2, 3, ... не
различаются между собой.
Н1: Эмпирические распределения 1, 2, 3, ...
различаются между собой.
Критерий 2 позволяет проверить все три варианта
гипотез.

7. Алгоритм расчета критерия 2

Алгоритм расчета критерия 2
1. Занести в таблицу наименования разрядов и
соответствующие им эмпирические частоты (первый
столбец).
2. Рядом с каждой эмпирической частотой записать
теоретическую частоту (второй столбец).
3. Подсчитать разности между эмпирической и
теоретической частотой по каждому разряду
(строке) и записать их в третий столбец.

8.

4. Определить число степеней свободы по формуле:
= k-1
где k - количество разрядов признака.
Если =1, внести поправку на "непрерывность".
5. Возвести в квадрат полученные разности и занести
их в четвертый столбец.
6. Разделить полученные квадраты разностей на
теоретическую частоту и записать результаты в пятый
столбец.
7. Просуммировать значения пятого столбца.
Полученную сумму обозначить как 2эмп.

9.

8. Определить по таблице критические значения для
данного числа степеней свободы .
Если 2эмп меньше критического значения, расхождения
между распределениями статистически недостоверны.
Если 2эмп равно критическому значению или
превышает его, расхождения между распределениями
статистически достоверны.
При сопоставлении эмпирических распределений
одного и того же признака следует вместо
теоретических частот подставлять эмпирическую
частоту второй выборки.

10.

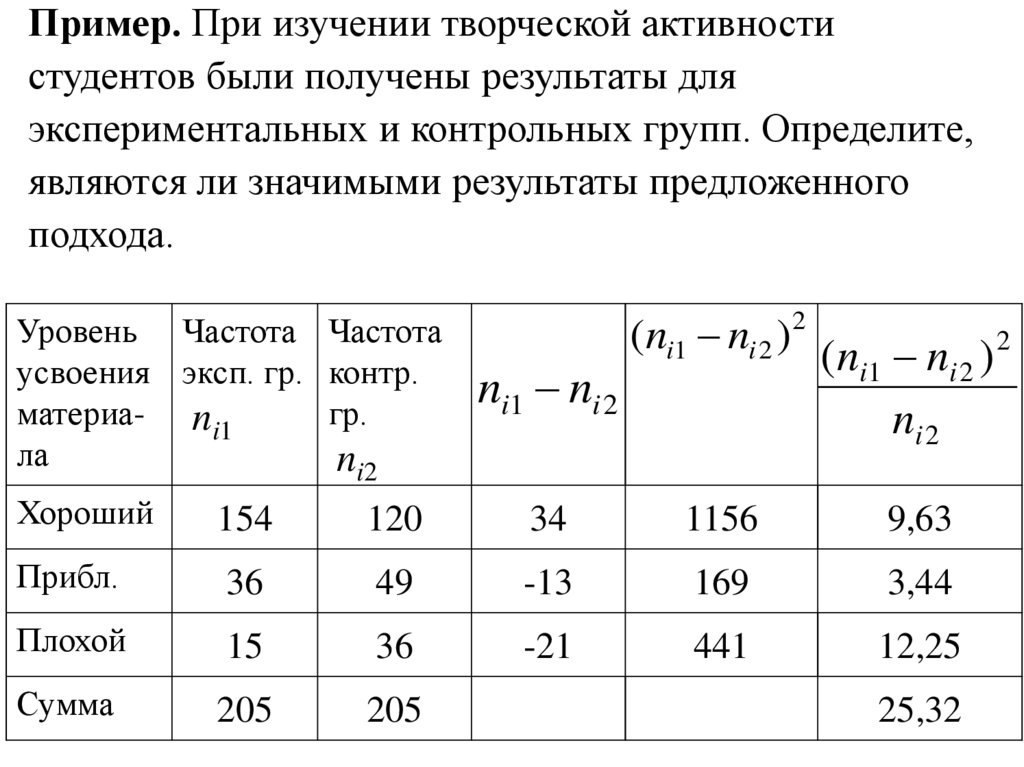
Пример. При изучении творческой активности
студентов были получены результаты для
экспериментальных и контрольных групп. Определите,
являются ли значимыми результаты предложенного
подхода.
Уровень Частота Частота
усвоения эксп. гр. контр.
материа- ni1
гр.
ла
ni2
ni1 ni 2
(ni1 ni 2 )
2
( ni 1 ni 2 )
ni 2
Хороший
154
120
34
1156
9,63
Прибл.
36
49
-13
169
3,44
Плохой
15
36
-21
441
12,25
Сумма
205
205
25,32
2

11.

2эмп=25,32
2кр=9,21 для α=0,01 и = 2 (стр. 328).
Поскольку 2эмп > 2кр (25,32 > 9,21) , то нулевая
гипотеза опровергается на высоком уровне
значимости. Это позволяет признать, что разница
частот контрольного и экспериментального ряда
является статистически достоверной.

12.

13.

λ - критерий Колмогорова-Смирнова
λ
критерий
Колмогорова-Смирнова
является
многофункциональным критерием и относится к группе
так называемых критериев согласия, предназначенных для
проверки гипотез о предполагаемом законе распределения.
Можно отметить, что название критерия является
обобщенным названием группы статистических критериев,
статистики
которых
определяются
с
помощью
максимального значения разности между (выборочной и
теоретической) функциями распределений или же их
оценками. Существуют критерии Колмогорова-Смирнова
для одной, двух и нескольких выборок.

14.

Одновыборочный
критерий
предназначен
для
сопоставления эмпирического и теоретического законов
распределений. Необходимость такого сравнения связана с
тем, что исследователь в ряде случаев не может заранее
точно знать, по какому именно закону распределены
полученные значения исследуемого признака, а может
только предположить, что распределение подчинено тому
или иному закону, например, нормальному. В такой
ситуации для установления истинного вида закона
распределения ему необходимо проверить статистические
гипотезы следующего вида:
H0: распределение исследуемого признака подчинено
некоторому закону распределения.
H1: распределение исследуемого признака отлично от
некоторого закона распределения.

15.

Двухвыборочный критерий Колмогорова-Смирнова
предназначен для сопоставления двух эмпирических
распределений. Предположим, что исследователем получены
две независимые случайные выборки x1, x2, ..., xn из совокупности с функцией распределения F(x),
y1, y2, ..., yn из совокупности с функцией распределения G(y).
Зачастую исследователь должен решить вопрос - получены
ли две выборки из одной и той же генеральной совокупности,
т.е. подчиняются ли они одному закону распределения, или
нет? Для выяснения этого вопроса необходимо проверить
следующие гипотезы:
H0: Различия между двумя распределениями имеют
случайный характер и, следовательно, недостоверны .
H1: Различия между двумя распределениями статистически
достоверны.

16.

Для применения критерия по двум выборкам определяют
две эмпирические функции распределения Fn1(x) и Gn2(y).
Статистика двухвыборочного λ - критерий КолмогороваСмирнова основывается на определении величины
Dn1,n2 = sup|Fn1(z)- Gn2(z)| ,
которая является наибольшим отклонением между двумя
эмпирическими функциями распределения (символ sup
означает наибольшее). Таким образом, для применения
критерия Колмогорова-Смирнова необходимо найти максимум
отклонения эмпирических распределений сравниваемых
выборок. Критерий позволяет определить точку, в которой
сумма накопленных расхождений (накопленных частостей)
между двумя распределениями является наибольшей, и
оценить статистическую достоверность этого расхождения.

17.

Условием применимости рассматриваемого критерия
является достаточный объем наблюдений - необходимо,
чтобы выборки были достаточно большими. Так для
сравнения двух эмпирических распределений необходимо,
чтобы n1 и n2 было больше 50. При сравнении
эмпирического и теоретического распределений иногда
допустим меньший объем выборки (n >5).

18.

Алгоритм применение λ критерия при
сопоставлении двух эмпирических распределений
1. Задаться уровнем значимости α и сформулировать
статистические гипотезы.
2. Построить эмпирические распределения: разбить
диапазон варьирования признака на интервалы
группировки, произвести группировку вариант,
определить соответствующие частоты и частости,
накопленные частоты и накопленные частости и
составить соответствующие интервальные
вариационные ряды. Для удобства можно составить
таблицу, в колонках которой будут располагаться
номера интервалов группировки, их интервалы,
частоты, частости, накопленные частоты и
накопленные частости.

19.

3. Определить абсолютные величины разностей
накопленных частостей двух выборок для каждого
интервала группировки.
4. Определить наибольшую абсолютную величину
разности накопленных частостей.
Dn1 ,n2 sup | F1i F2i |
5. Вычислить эмпирическое значение критерия λэмп с
помощью соотношения
эмп Dn1 ,n2
n1n2
n1 n2

20.

6. По специальной таблице определить критическое значение
λкр критерия Колмогорова-Смирнова для выбранного
уровня значимости α. Для стандартных уровней
значимости α=0,05 и α=0,01 критические значения равны
λкр0,05=1,36 и λкр0,01=1,63
7. Сравнить полученные эмпирическое (λэмп) и критическое
(λкр) значения критерия. Если эмпирическое значение
критерия не превышает критическое (λэмп≤λкр), то различия
между двумя распределениями носят случайный характер и
выборки получены из одной генеральной совокупности. В
противном случае (λэмп>λкр) различия между
распределениями статистически достоверны и выборки
относятся к различным генеральным совокупностям.

21.

Пример. В проведении сборов участвуют две группы
спортсменов, представляющие два спортивных клуба.
Результаты,
показанные
спортсменами
и
представленные в виде интервальных вариационных
рядов, представлены в таблице. В колонках таблицы
представлены частоты (n1i; n2i), частости (f1i; f2i) и
накопленные
частости
(F1i;
F2i).
Определить,
различаются ли законы распределения результатов,
показанных спортсменами двух групп.