Похожие презентации:
Проверка статистических гипотез
1. Проверка статистических гипотез
ПРОВЕРКАСТАТИСТИЧЕСКИХ
ГИПОТЕЗ
2. Статистическая гипотеза -
СТАТИСТИЧЕСКАЯ ГИПОТЕЗА это гипотезао видах неизвестного распределения или
о параметрах известного распределения.
Проверка статистической
гипотезы:
заключается в сопоставлении некоторых
статистических показателей, вычисленных
по данным выборки со значениями этих же
показателей, определенных теоретически в
предположении, что проверяемая гипотеза
верна.
3. Классификация гипотез
КЛАССИФИКАЦИЯ ГИПОТЕЗВыдвинутая (нулевая)
Конкурирующая (альтернативная).
Выдвинутая (нулевая) гипотеза Н0 – гипотеза,
подлежащая проверке.
Конкурирующая (альтернативная) гипотеза Н1 –
каждая допустимая гипотеза, отличная от
нулевой.
Пример:
Если Н0 состоит в предположении, что математическое
ожидание М(Х) нормального распределения равно 10,
то Н1 может состоять в предположении, что М(Х) не
равно 10.
Н0: М(Х)=10.
Н1: М(Х)≠10
4. Классификация гипотез
КЛАССИФИКАЦИЯ ГИПОТЕЗПо количеству предположений:
простые, сложные.
Простая – это гипотеза содержащая
только одно предположение.
Сложная – гипотеза состоящая из
конечного или бесконечного числа
простых гипотез.
5. Примеры:
ПРИМЕРЫ:Если λ – параметр распределения
Пуассона, то гипотеза H0: λ = 5 является
простой.
Нулевая гипотеза о том, что
математическое ожидание нормального
распределения равно 3 (при известной
дисперсии) H0 : а=3 также является
простой.
Сложная гипотеза H0 : λ >7 состоит из
множества простых гипотез вида Hi : λ=ki ,
где ki - любое число, большее семи.
6. Ошибки проверки статистических гипотез
ОШИБКИ ПРОВЕРКИ СТАТИСТИЧЕСКИХГИПОТЕЗ
Ошибка первого рода или «ложная тревога» состоит
в том, что будет отвергнута правильная гипотеза.
Вероятность ошибки первого рода называется
уровнем значимости и обозначается α.
Ошибка второго рода или «пропуск цели» состоит
в том, что будет принята неправильная гипотеза.
Вероятность ошибки второго рода обозначается .
Величина 1- называется мощностью критерия.
На практике, наиболее часто используют α=0,05,
это означает, что в 5 случаях из 100 имеется риск
допустить ошибку первого рода, т.е. отвергнуть
правильную гипотезу.
7.
РЕЗУЛЬТАТЫ ПРОВЕРКИСТАТИСТИЧЕСКИХ ГИПОТЕЗ
8. Статистический критерий
СТАТИСТИЧЕСКИЙ КРИТЕРИЙДля проверки Н0, используют специально
подобранную случайную величину, точное или
приближенное значение которой известно.
Эту величину обозначают через:
U или Z, если она распределена нормально;
F или ² - по закону Фишера;
² - по закону «хи квадрат»;
Т или t - по распределению Стьюдента.
Статистическим критерием называют
случайную величину, служащую для проверки Н0.
Наблюдаемым значением критерия называют
значение критерия, выраженное по данным
выборки.
9. Критическая область
КРИТИЧЕСКАЯ ОБЛАСТЬПосле выбора определенного критерия
множество всех его возможных значений
разбивается на два подмножества:
содержит значения критерия, при котором Н0
отвергается;
содержит значения критериев, при которых Н0
принимается.
Критической областью называют, совокупность
значений критерия, при которой Н0 отвергается.
Областью принятия гипотезы (областью
допустимых значений), называют совокупность
значений критерия, при которой Н0 принимают.
10.
Основной принцип проверкистатистических гипотез:
если наблюдаемое значение критерия принадлежит
критической области, то гипотезу отвергают;
если наблюдаемое значение критерия принадлежит
области покрытия гипотезы, то гипотезу принимают.
Критическая область и область покрытия гипотез –
это интервалы, следовательно существует точка
которая их разделяет.
Критической точкой (границей), называют точку
(квантиль), отделяющую критическую область от
области принятия гипотез.
11.
Типы критической области1. Односторонняя критическая область:
Левосторонняя - определяемая неравенством К<Ккр
Правосторонняя - определяемая неравенством К>Ккр
2. Двусторонняя критическая область –
определяемая двумя неравенствами
К<Кı и К>К2; Кı>К2
12.
При отыскании критической области задают α(уровень значимости)
Ищут критические точки, исходя из требований, что
критерий К примет значение, лежащее в критической
области.
При этом вероятность такого события равна
принятому уровню значимости α, т.е.
для правосторонней области Р(К>Ккр)= α;
для левосторонней области Р(К<Ккр)= α;
для двусторонней области Р(К>|Ккр|)= α/2
Если наблюдаемое значение критерия принадлежит
критической области, нулевую гипотезу отвергают,
если не принадлежит, то нет оснований отвергать Н0.
Для многих критериев составлены таблицы:
Стьюдента; χ²; Фишера
13. Общая схема проверки гипотез
ОБЩАЯ СХЕМА ПРОВЕРКИ ГИПОТЕЗ1. Формулируются гипотезы Н0 и Н1.
2. Выбирается уровень значимости критерия . Он равен
вероятности допустить ошибку первого рода.
3. По выборочным данным вычисляется значение некоторой
случайной величины, называемой статистикой критерия, или
просто статистическим критерием, который имеет известное
стандартное распределение (нормальное, Т-распределение
Стьюдента и т.п.)
4. Вычисляется критическая область и область принятия гипотезы.
То есть находят критическое (граничное) значение критерия при
выбранном уровне значимости.
5. Найденное значение критерия сравнивается с критическим и по
результатам сравнения делается вывод: отвергнуть гипотезу или
не отвергнуть.
Если вычисленное по выборке значение критерия меньше чем
критическое, то нулевую гипотезу Но не отвергают на заданном
уровне значимости.
Если вычисленное значение критерия больше критического, то
гипотеза Н0 отклоняется в пользу гипотезы Н1 при данном уровне
значимости.
14. Критерии значимости
КРИТЕРИИ ЗНАЧИМОСТИ1. Параметрические - критерии значимости, которые
служат для проверки гипотез о параметрах
распределений генеральной совокупности (чаще
всего нормального распределения). Эти критерии
называются параметрическими.
2. Непараметрические - критерии, которые для
проверки гипотез не используют предположений о
распределении генеральной совокупности. Эти
критерии не требуют знания параметров
распределений.
3. Критерии согласия, служащие для проверки гипотез
о согласии распределения генеральной совокупности,
из которой получена выборка, с ранее принятой
теоретической моделью (чаще всего нормальным
распределением):
критерий
Пирсона;
критерий
Колмогорова; критерий Смирнова.
15. Проверка однородности выборок в прикладных задачах
ПРОВЕРКА ОДНОРОДНОСТИ ВЫБОРОК ВПРИКЛАДНЫХ ЗАДАЧАХ
В прикладных исследованиях часто возникает
необходимость выяснить:
различаются ли генеральные совокупности, из
которых взяты две независимые выборки;
изменилась ли генеральная совокупность после
воздействия.
В математико-статистических терминах постановка задачи
такова:
имеются две выборки x1, x2,...,xm и y1, y2,...,yn, требуется
проверить их однородность, т.е. требуется проверить, есть
ли различие между выборками.
Если имеющееся различие средних значений нельзя
объяснить случайными статистическими колебаниями,
то говорят о значимом различии.
16. Однородность выборок
ОДНОРОДНОСТЬ ВЫБОРОКПонятие «однородность», т. е. «отсутствие
различия», может быть формализовано в
терминах вероятностной модели различными
способами:
1 способ:
Обе выборки взяты из одной генеральной
совокупности, т. е. справедлива нулевая гипотеза
H0 : F(x)=G(x) при всех х.
Отсутствие однородности означает, что верна
альтернативная гипотеза, согласно которой
H1 : F(x0) G(x0) хотя бы при одном значении
аргумента x0.
Если гипотеза H0 принята, то выборки можно
объединить в одну, если нет - то нельзя.
17. 2 способ:
2 СПОСОБ:В некоторых случаях целесообразно проверять не совпадение
функций распределения, а совпадение некоторых
характеристик случайных величин Х и Y - математических
ожиданий, медиан, дисперсий, коэффициентов вариации и
др.
Например, однородность математических ожиданий
означает, что справедлива гипотеза
H'0 : M(X)=M(Y), где M(Х) и M(Y) - математические ожидания
случайных величин Х иY, результаты наблюдений над
которыми составляют первую и вторую выборки
соответственно.
Доказательство различия между выборками в
рассматриваемом случае - это доказательство
справедливости альтернативной гипотезы H'1 : M(X) M(Y) .
Если гипотеза H0 верна, то и гипотеза H'0 верна, но из
справедливости H'0 не следует обязательно справедливость
H0: математические ожидания могут совпадать для
различающихся между собой функций распределения.
18. Независимость выборок
НЕЗАВИСИМОСТЬ ВЫБОРОКЕсли можно установить гомоморфную пару (то есть,
когда одному случаю из выборки X соответствует один
и только один случай из выборки Y и наоборот) для
каждого случая в двух выборках (и это основание
взаимосвязи является важным для измеряемого
признака), такие выборки называются зависимыми.
Примеры зависимых выборок: пары близнецов, два
измерения какого-либо признака до и после
экспериментального воздействия и т. п.
В случае, если такая взаимосвязь между выборками
отсутствует, то эти выборки считаются независимыми,
например: психологи и математики.
Соответственно, зависимые выборки всегда имеют
одинаковый объём, а объём независимых может
отличаться.
19. Параметрические методы проверки однородности выборок
ПАРАМЕТРИЧЕСКИЕ МЕТОДЫ ПРОВЕРКИ ОДНОРОДНОСТИВЫБОРОК
Традиционный метод проверки однородности двух
независимых выборок (критерий Стьюдента)
Выдвигаются: нулевая гипотеза о равенстве
средних и альтернативная, о том, что средние не
равны.
Вычисляют выборочные средние арифметические
и дисперсии в каждой выборке и статистику
Стьюдента t, на основе которой принимают
решение.
По заданному уровню значимости и числу
степеней свободы (m+n - 2) из таблиц
распределения Стьюдента находят критическое
значение tкр.
Если |t| > tкр, то гипотезу однородности (отсутствия
различия) отклоняют, если же |t| <tкр,то принимают.
20. t-критерий можно использовать лишь при выполнении следующих условий:
T-КРИТЕРИЙ МОЖНО ИСПОЛЬЗОВАТЬ ЛИШЬ ПРИВЫПОЛНЕНИИ СЛЕДУЮЩИХ УСЛОВИЙ:
1.
Наблюдения в каждой из рассматриваемых
групп взяты случайным образом из одной и
той же генеральной совокупности
(например, две группы студентов одного
курса или дети одного возраста и т.д.)
2. Наблюдения имеют нормальные
распределения или объем каждой выборки
превышает 30 значений.
21.
ПРИМЕР.Табл. 1
Данные диагностики до начала экспериментального обучения
Студенты
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Баллы
14
16
16
17
17
18
18
18
18
18
20
20
24
25
27
27
27
28
28
28
все
го
42
4
Х
≈
21,
2
Табл. 2
Данные диагностики по окончании экспериментального обучения
Студенты
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Баллы
16
18
18
19
20
20
20
20
22
24
24
25
26
26
27
28
28
28
29
30
вс
ег
о
44
8
Х
24,
35
Задача:
выяснить с помощью
t-критерия Стьюдента, являются ли
различия в показателях до начала экспериментального обучения и
после такого обучения статистически значимыми.
22. Решение:
РЕШЕНИЕ:Для сравнения полученных результатов,
применив t – критерий Стьюдента
сформулируем гипотезы:
нулевая гипотеза H0 – разница между
показателями до экспериментального
обучения и после такого обучения имеет
лишь случайные различия;
альтернативная гипотеза H1 – разница
между показателями до экспериментального
обучения и после такого обучения имеет не
случайные различия.
23. Решение:
РЕШЕНИЕ:Для равночисленных выборок Д1 и Д2
t эмп
X Y
=
х у у у
2
i
n 1 n
2
i
ВЫВОД. Так как t эмп2 больше t кр, то гипотеза H0 отклоняется и
принимается гипотеза H1 . Это означает, что разница между
показателями до экспериментального обучения и после такого
обучения имеет не случайные различия.
24. Сравнение среднего с нормативом (t-тест одной выборки)
СРАВНЕНИЕ СРЕДНЕГО С НОРМАТИВОМ(T-ТЕСТ ОДНОЙ ВЫБОРКИ)
Этот тест позволяет выяснить, отличается ли среднее
значение, полученное на основе данной выборки, от
предварительно заданного контрольного значения.
Выдвигаются гипотезы
Вычисляется значение статистики t по формуле
Значимость отличия среднего от заданного значения
определяется на основании сравнения полученной статистики t
с критической или в зависимости от полученной величины
наблюдаемого уровня значимости.
Если наблюдаемый уровень значимости меньше необходимого
(например, 0,05), то считается, что среднее значение
существенно отличается от нормативной величины.
25. Сравнение двух независимых выборок. Тест Колмогорова-Смирнова
СРАВНЕНИЕ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК.ТЕСТ КОЛМОГОРОВА-СМИРНОВА
Данный критерий позволяет оценить существенность
различий между двумя выборками. Его применение возможно
также для сравнения эмпирического распределения с
теоретическим.
Объёмы рассматриваемых выборок должны
быть достаточно большими: n1 ≥50, n2 ≥50.
Для использования теста выборки должны быть
представлены в виде частотного распределения, при этом
число категорий должно быть небольшим (до 7-9).
Нулевая гипотеза H0={различия между двумя
распределениями недостоверны}.
Критерий позволяет найти категорию, в которой сумма частот
расхождений между двумя распределениями является
наибольшей, и оценить достоверность этого расхождения.
26. Алгоритм проверки:
АЛГОРИТМ ПРОВЕРКИ:1.
2.
3.
4.
5.
6.
7.
8.
Определяются категории значений признака.
Строится частотное распределение каждой выборки по
выделенным категориям.
Вычисляются относительные частоты f, равные частному
от деления частот на объём выборки, для каждой из
имеющихся выборок.
Определяется модуль разности соответствующих
относительных частот.
Определяется наибольший модуль, который
обозначается dmax.
Вычисляется эмпирическое значение критерия эмп:
Определяется критическое значение критерия для
выбранного уровня значимости.
Если эмпирическое значение критерия больше
критического, то нулевая гипотеза отвергается, и группы по
рассмотренному признаку отличаются существенно.
27. Пример сравнения двух независимых выборок с использованием теста Колмогорова-Смирнова
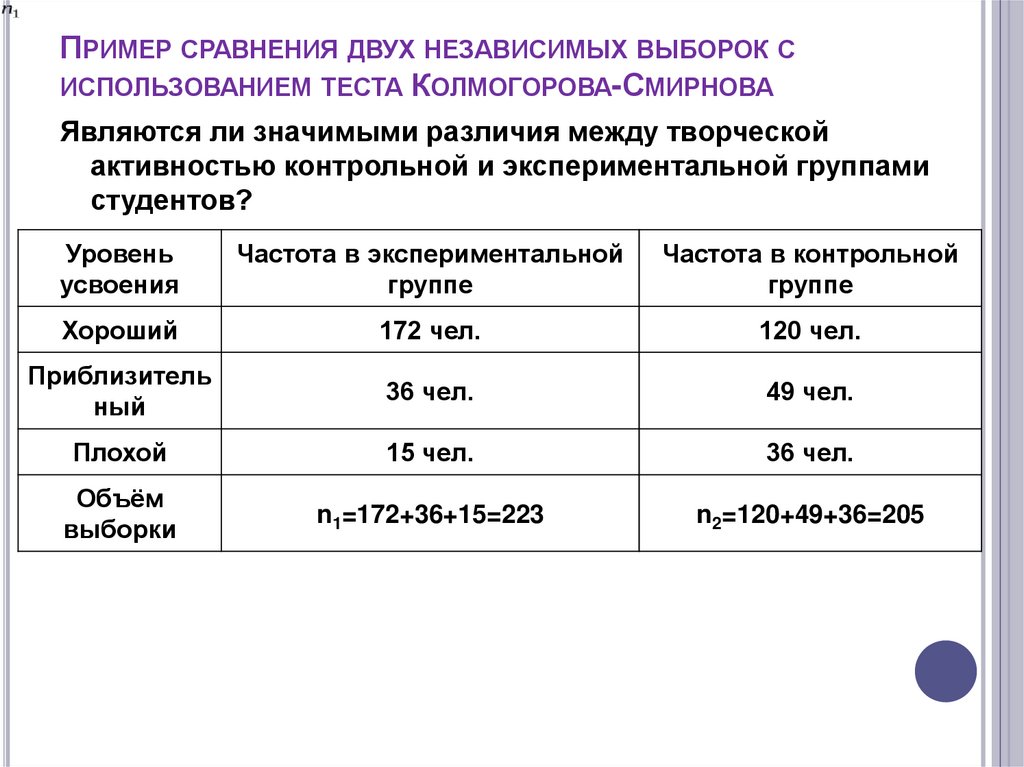
ПРИМЕР СРАВНЕНИЯ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК СИСПОЛЬЗОВАНИЕМ ТЕСТА КОЛМОГОРОВА-СМИРНОВА
Являются ли значимыми различия между творческой
активностью контрольной и экспериментальной группами
студентов?
Уровень
усвоения
Частота в экспериментальной
группе
Частота в контрольной
группе
Хороший
172 чел.
120 чел.
Приблизитель
ный
36 чел.
49 чел.
Плохой
15 чел.
36 чел.
Объём
выборки
n1=172+36+15=223
n2=120+49+36=205
28.
Вычисляем относительные частоты , равные частному от деления частотна объём выборки, для каждой из имеющихся выборок.
Определяем модуль разности соответствующих относительных частот
для контрольной и экспериментальной выборок.
В результате исходная таблица примет следующий вид:
Относительная частота
экспериментальной группы
(fэксп)
Относительная частота
контрольной группы (fконтр)
Модуль разности частот
|fэксп – fконтр|
172/223≈0.77
120/205≈0.59
0.18
36/223≈0.16
49/205≈0.24
0.08
15/223≈0.07
36/205≈0.17
0.1
Среди полученных модулей разностей относительных частот выбираем
наибольший модуль, который обозначается dmax=0.18.
Эмпирическое значение критерия λэмп определяется с помощью
формулы:
Считая, что =0,05, по таблице определяем критическое значение
критерия:
следовательно, нулевая гипотеза отвергается, и группы по
рассмотренному признаку отличаются существенно.
29. Сравнение двух дисперсий
СРАВНЕНИЕ ДВУХ ДИСПЕРСИЙРассмотрим гипотезу о параметрах нормального распределения. Пусть
имеется две серии опытов, регистрирующие значение некоторой
случайной величины.
Х: х1, х2 … хn
Y: y1, y2 … уn
Осуществим проверку нулевой гипотезы о равенстве дисперсий при
неизвестных математических ожиданиях.
Н0: Dx =Dy
Постановка задачи.
Пусть даны две случайные величины Х и Y, распределенные нормально.
По данным выборки объем их nx и ny подсчитаны выборочные дисперсии.
Цель работы: при заданном уровне значимости α проверить нулевую
гипотезу о равенстве дисперсий.
Такая задача возникает при сравнении точности двух приборов, или при
сравнении различных методов измерения. Т.е. когда выборочные
дисперсии отличаются, возникает вопрос значимости или не значимости
этого различия.
Если различие неразличимо, то имеет место нулевая гипотеза, т.е.
приборы, например, имеют одинаковую точность. А различия
выборочных дисперсий объясняются случайными причинами.
30. Механизм проверки
МЕХАНИЗМ ПРОВЕРКИПо данным выборок значений nх и nу, вычисляют наблюдаемое
значение критерия как отношение большей дисперсии к меньшей:
2
2
2
max(S
,
S
x
y)
S большая
Fнабл
Fнабл 2
min(S 2x , S 2y )
S
меньшая
Критическая область строится в зависимости от конкурирующей
гипотезы.
По таблицам распределения Фишера, по заданному уровню
значимости α и вычисленным степеням свободы υx, υy находят
табличное значение критерия:
для альтернативной гипотезы Н1: Dx >Dy
Fкр в зависимости от параметров Fкр (α, υx, υy)
для альтернативной гипотезы Н1: Dx ≠ Dy
Fкр в зависимости от параметров Fкр (α/2, υx, υy)
Если Fнаб >Fкр, то Н0 отвергают.
Если Fнаб <Fкр, то нет оснований отвергать Н0,
предположение о том что Dx, Dy, принимается с уровнем α,
в 95% случаях – с доверительной вероятностью.
31.
ПРИМЕР:По двум малым независимым выборкам объемов nx=11 и ny=14
из нормальных распределений найдены исправленные
выборочные дисперсии S²x =0.76 и S2y=0.38. При уровне
значимости α=0.05 проверить нулевую гипотезу Н0: Dx=Dy о
равенстве дисперсий при конкурирующей гипотезе Н1: Dx>Dy.
Решение: Найдем отношение большей исправленной дисперсии к
меньшей:
Fнабл = S²б / S²м = 0.76 / 0.38 = 2
По условию конкурирующая гипотеза имеет вид Н1: Dx>Dy,
поэтому критическая область – правосторонняя. По таблице
критических точек распределения Фишера, по уровню значимости
α=0,05 и числам степеней свободы k1 = nx – 1 = 11 – 1 = 10 и
k2 = ny – 1 = 14 – 1 = 13 находим критическую точку:
Fкр (α, kı, k2) = Fкр (0.05,10,13) = 2.67
Так как Fнабл = 2. < Fкр = 2.67, то нет оснований отвергать Но о
равенстве дисперсий.
Другими словами, исправленные выборочные дисперсии
различаются незначимо.
32. Сравнение мат.ожиданий
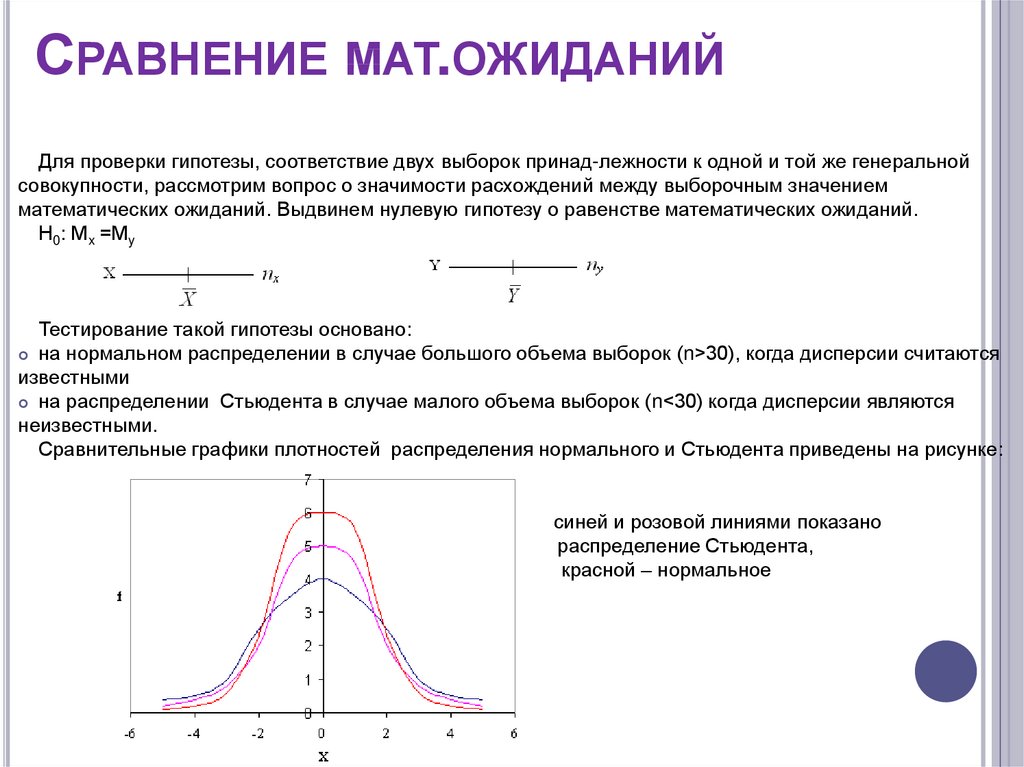
СРАВНЕНИЕ МАТ.ОЖИДАНИЙДля проверки гипотезы, соответствие двух выборок принад-лежности к одной и той же генеральной
совокупности, рассмотрим вопрос о значимости расхождений между выборочным значением
математических ожиданий. Выдвинем нулевую гипотезу о равенстве математических ожиданий.
Н0: Мx =Мy
Тестирование такой гипотезы основано:
на нормальном распределении в случае большого объема выборок (n>30), когда дисперсии считаются
известными
на распределении Стьюдента в случае малого объема выборок (n<30) когда дисперсии являются
неизвестными.
Сравнительные графики плотностей распределения нормального и Стьюдента приведены на рисунке:
синей и розовой линиями показано
распределение Стьюдента,
красной – нормальное
33. Проверка гипотезы о равенстве средних при известных дисперсиях
ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХПРИ ИЗВЕСТНЫХ ДИСПЕРСИЯХ
Для того чтобы при заданном уровне значимости α =0.05 проверить нулевую гипотезу Н0:
Мх=Му о равенстве математических ожиданий двух больших нормальных выборок с известными
дисперсиями Dх и Dу, необходимо:
1. Вычислить наблюдаемое значение критерия:
Dx D y
Z набл X Y
nx n y
Построить критическую область в зависимости от конкурирую-щей гипотезы:
при конкурирующей гипотезе Н1: Мх ≠ Му по таблице функции Лапласа находят критическую
точку zкр из равенства Ф(zкр) = (1 – α) /2.
Если |Zнабл| < zкр, то нет оснований отвергать нулевую гипотезу.
Если |Zнабл| > zкр, то нулевую гипотезу отвергают.
при конкурирующей гипотезе Н1: Мх > Му по таблице функции Лапласа находят критическую
точку zкр из равенства
Ф(zкр) = (1 – 2α) /2.
Если Zнабл < zкр, то нет оснований отвергать нулевую гипотезу.
Если Zнабл > zкр, то нулевую гипотезу отвергают.
при конкурирующей гипотезе Н1: Мх < Му по таблице функции Лапласа находят
«вспомогательную критическую точку» zкр из равенства
Ф(zкр) = (1 – 2α) /2.
Если Zнабл > - zкр, то нет оснований отвергать нулевую гипотезу.
Если Zнабл < - zкр, то нулевую гипотезу отвергают.
34. Проверка гипотезы о равенстве средних при неизвестных дисперсиях
ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХПРИ НЕИЗВЕСТНЫХ ДИСПЕРСИЯХ
Постановка задач: пусть генеральные совокупности
распределены нормально, причем их дисперсии Dx и Dy
заранее не известны. Взяты две выборки малого объема,
требуется сравнить средние этих генеральных
совокупностей.
Методика проверки задач: заключается в использовании
критерия Стьюдента при условии, что генеральные
дисперсии не известны, однако в предположении, что они
равны между собой.
Такая задача возникает: если сравниваются средние
размеры двух партий деталей, изготовленных на одном и том
же станке. Естественно будет предположить, что дисперсии
контролируемых размеров одинаковы.
35. Алгоритм проверки
АЛГОРИТМ ПРОВЕРКИ1) Прежде чем сравнивать средние требуется проверить Н0: Dх=Dу
2) Если гипотеза подтвердилась нужно вычислить наблюдаемое значение критерия:
Тн
Х Y
x S x2 y S y2
nx n y (nx n y 2)
nx n y
3) Строим критическую область в зависимости от конкурирующей гипотезы
а) Если Н1: Мх ≠ Му – двусторонняя критическая область строится исходя из условия чтобы
вероятность попадания наблюдаемого значения критерия в эту область была равна принятому уровню
значимости α взятого из таблицы Стьюдента для числа степеней свободы в верхней части таблицы, т.е.
для двусторонней критической области при условии |Тнабл| < tкр(α,υ), то нет основания отвергать
нулевую гипотезу; если |Тнабл| > tкр(α,υ), то нулевую гипотезу отвергают.
б) Если Н1: Мх >Му строится правосторонняя критическая область, а критическую точку находят по
таблице Стьюдента из нижней части.
Если Тнабл < tкр, то нет основания отвергать нулевую гипотезу .
Если Тнабл > tкр, то нулевую гипотезу отвергают.
в) При конкурирующей гипотезе Н1: Мх < Му по таблице критических точек распределения Стьюдента,
по заданному уровню значимости α,помещенному в нижней строке таблицы ,и числу степеней свободы
k= nх + nу–2 найти «вспомогательную критическую точку» tкр односторонней критической области.
2
Если Тнабл < - tкр, то нет основания отвергать нулевую гипотезу.
2
2
2
S
S
y
Если Тнабл > - tкр, то нулевую гипотезу отвергают.
x
Тнабл и число степеней свободы.
Т набл X Y
2
S x2 S y
nx n y
2
S x2 S y
nx n y
n n
x y
x
y
36. Проверка гипотезы о законе распределения генеральной совокупности
ПРОВЕРКА ГИПОТЕЗЫ О ЗАКОНЕРАСПРЕДЕЛЕНИЯ ГЕНЕРАЛЬНОЙ
СОВОКУПНОСТИ
Если закон распределения не известен, но есть основание
предположить, что он имеет определенный вид (А), то проверяют нулевую
гипотезу:
Н0: генеральная совокупность распределена по закону А.
Проверка гипотезы о предполагаемом законе распределения
производится так же, как и проверка гипотезы о параметрах
распределения, т.е. при случайно отобранной случайной величине –
критерия согласия.
Критерием согласия называют критерий проверки гипотезы о
предполагаемом законе распределения.
Имеется несколько критериев согласия:
критерий Пирсона;
критерий Колмогорова;
критерий Смирнова.
37. Критерий Пирсона
КРИТЕРИЙ ПИРСОНАПусть по выборке объема n получены эмпирические частоты, т.е. мы имеем
предполагаемое
распределение.
Допустим, что в предположении нормального распределения
xi x1 x2 x3 x4 x5
генеральной совокупности вычислены
теоретические частоты.
ni n 1 n 2 n 3 n 4 n 5
При уровне значимости α требуется проверить гипотезу:
генеральная совокупность распределена нормально.
В качестве критической проверку нулевой гипотезы примем случайную величину:
(ni ni ) 2 (*)
2
расчет
ni
Эта величина случайная, т.к. в различных опытах она принимает различные, заранее не
известные, значения. Чем меньше различаются эмпирические и теоретические частоты,
тем меньше величина критерия => он характеризует близость эмпирических и
теоретических распределений.
Доказано, что закон распределения случайной величины (*) не зависит от того, какому
закону распределения подчинена генеральная совокупность, а стремится к закону
распределения χ2 с числом степеней свободы: υ=k–1–r , где
k – число групп (интервалов) выборки
r – число параметров предполагаемого распределения.
А т.к. для нормального распределения нам интересно М(х) и D(x), то число степеней
свободы определяется υ=k–3
38.
39. Правила проверки
ПРАВИЛА ПРОВЕРКИДля того, чтобы при заданном уровне значимости α проверить Н0: “генеральная
совокупность распределена нормально”, необходимо:
1.вычислить теоретические частоты;
(ni ni ) 2
2
2.вычислить наблюдаемое значение критерия: набл
ni
3.по таблицам критических точек распределения χ2 по заданному уровню значимости и
числу степеней свободы υ=k–3, найти критическую точку: χ2кр=(α,υ);
4.сравнить 2 имеющихся критерия:
- если χ2набл< χ2кр - нет основания отвергать нулевую гипотезу о нормальном
распределении.
- если χ2набл > χ2кр - нулевую гипотезу о нормальном распределении отвергают.
Замечание:
объем выборки должен быть достаточно велик (более 50);
малочисленные группы следует объединять в одну, суммируя частоты;
т.к. возможные ошибки первого и второго рода, то в окончательном выводе следует
проявить осторожность:
можно повторить опыт;
увеличить число наблюдений;
для проверки воспользоваться другими критериями;
построить график распределения;
(ni ni ) 2
2
2
вычислить эксцесс и асимметрию. набл
n
2
i
ni
набл ( ) n
ni
для контроля вычислений формулу преобразуют к виду




































 Математика
Математика








