Многокритериальные задачи принятия решения Методы построения эффективных множеств

1. Многокритериальные задачи принятия решения Методы построения эффективных множеств

2. Следует повторить

Постановка многокритериальных ЗПР
– Критерий
Скалярный
Векторный
Позитивный
Негативный
– Решение многокритериальной задачи
Идеальное
Компромиссное
– Пространство альтернатив
– Пространство векторных оценок
– Альтернативы
Сравнимые
Несравнимые
Доминирующие
Доминируемые

3. Входной контроль

4. Самопроверка

5. План лекции

• Парето оптимальные альтернативы и Парето
оптимальные оценки.
• Общая технологическая схема принятия решений при
многих критериях.

6.

15.07.1848-20.08.1923
Впервые задачей многокритериальной (векторной) оптимизации
занялся итальянский экономист В. Парето при математическом
исследовании товарного объекта. В 1896 В.Парето предложил в
экономике концепцию, получившую название принципа Паретооптимальности.

7. Парето оптимальность

Определение 1. Альтернатива x X доминирует (по Парето) альтернативу
1
1 P 2 если f ( x 1 ) f ( x 2 ), i 1, m
x X x x
i
i
такое, что f ( x 1) f ( x 2 )
i0
i0
2
и
i0 , i0 {1, m}
Определение 2. Альтернатива x X оптимальна по Парето (эффективна)
*
если не существует x X , доминирующей x *
X
x1 x2 x3
f1 x
2
4
3
f2 x
5
1
6
x
3
P
x1
X ý x2, x3
P
x3
P
x1
X ý x4 , x5 , x7 , x8
M1 M 2
X э Q, B

8.

9.

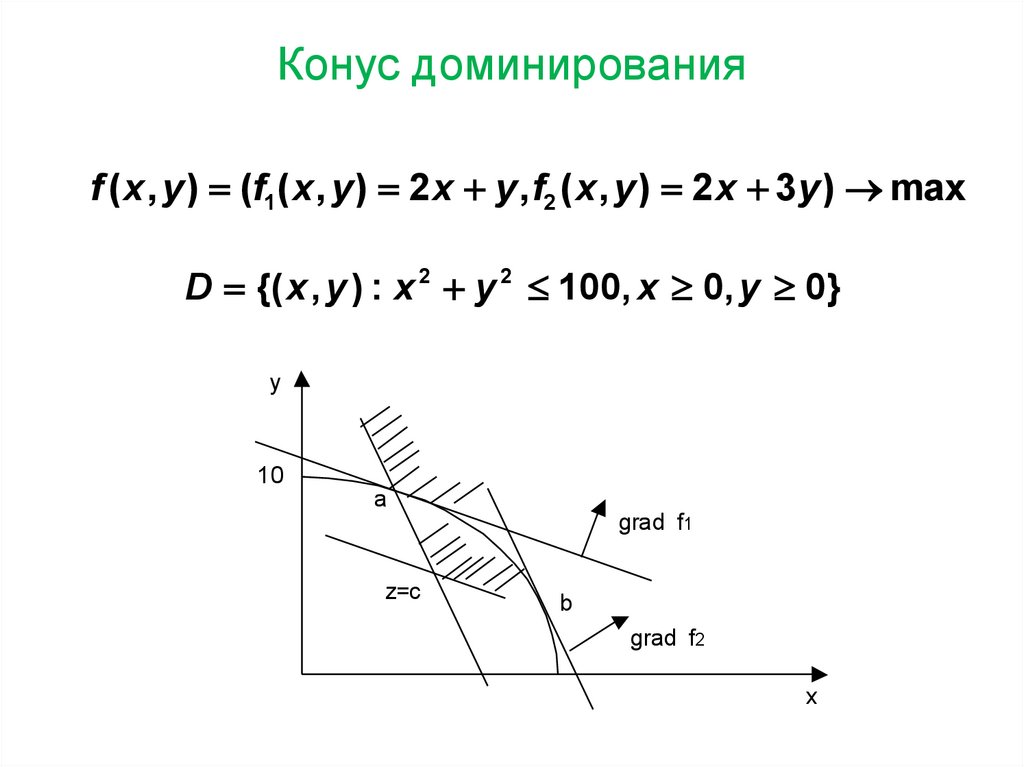
Конус доминирования
f ( x , y ) (f1( x , y ) 2 x y , f2 ( x , y ) 2 x 3y ) max
D {( x , y ) : x 2 y 2 100, x 0, y 0}
y
10
a
grad f1
z=c
b
grad f2
x

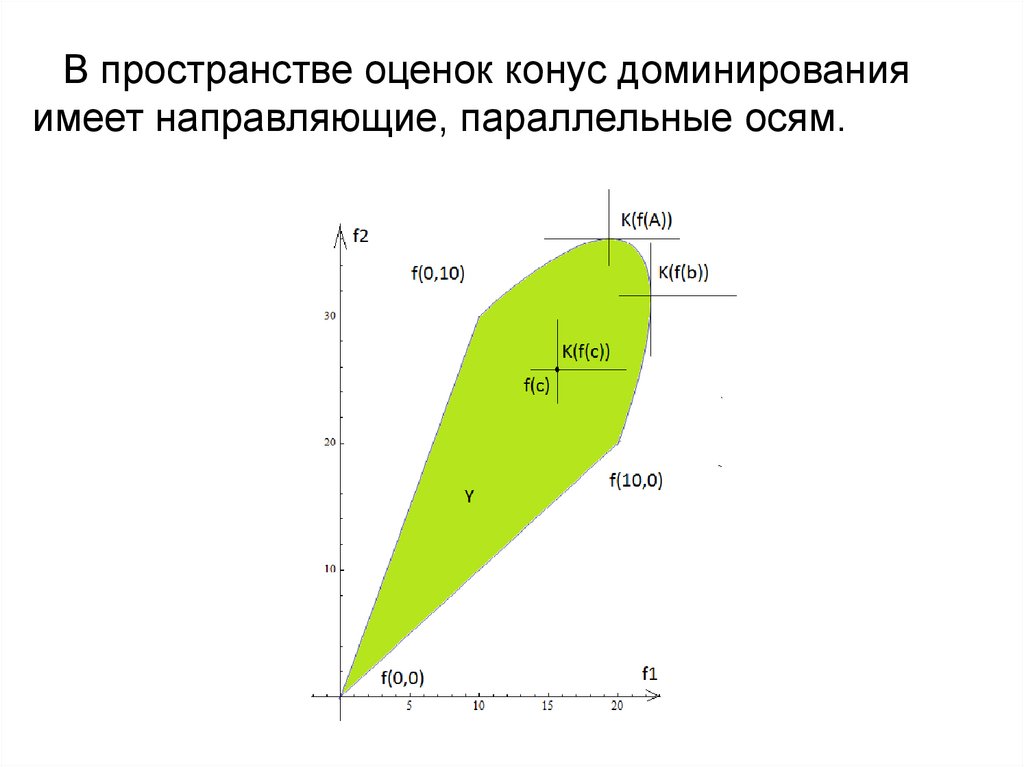
10.

В пространстве оценок конус доминирования
имеет направляющие, параллельные осям.

11.

Пример 2. f (x)=(f1=cos x, f2=tg x) max, X=[0,1].
XЭ=[0,1].
f(x)
f2
f1
x
0
x
1

12.

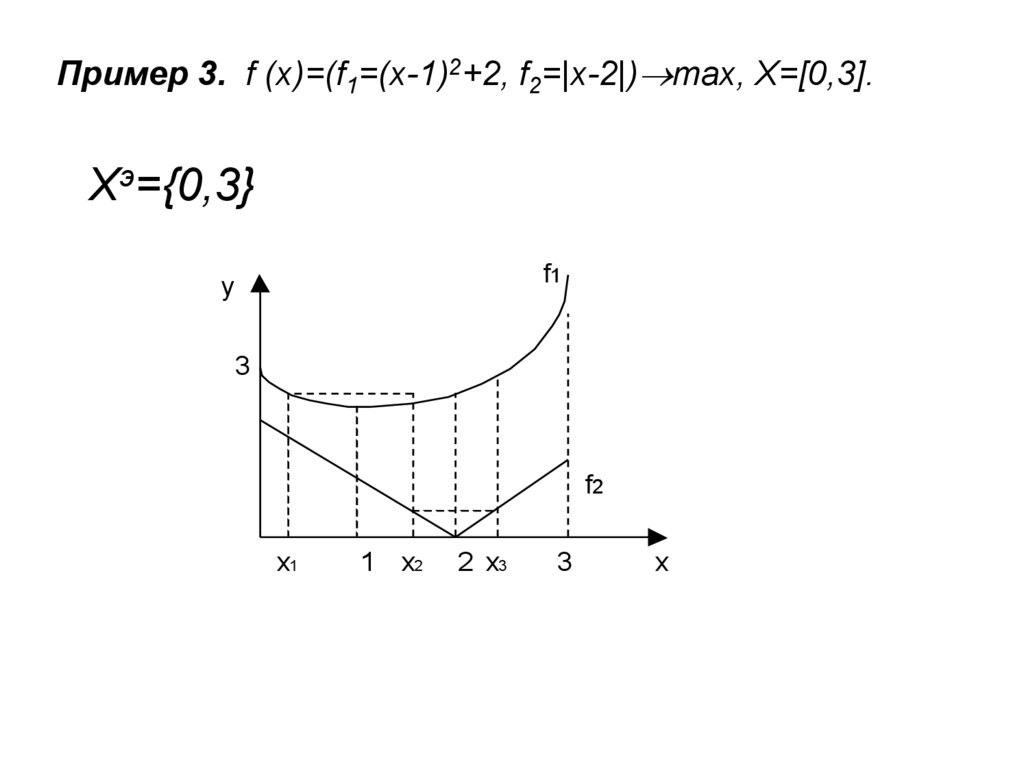
Пример 3. f (x)=(f1=(x-1)2+2, f2=|x-2|) max, X=[0,3].
Xэ={0,3}
f1
y
3
f2
x1
1
x2
2 x3
3
x

13. Методы решения многокритериальных задач

Методы решения многокритериальных
задач
Описание выбора
на языке
бинарных отношений
Критериальный язык описания
выбора
интерактивные
Метод анализа
иерархий
Метод
эффективных
множеств
Лексикографическая оптимизация
Метод
уступок
Аддитивные
Главного
критерия
Мультипликативные
Автоматические (сведение к
однокритериальным)
свертки
Целевого
программирования
Максиминные

14. Резюме

Парето оптимальные альтернативы
Парето оптимальные оценки