Похожие презентации:
Касательная к окружности
1.
КАСАТЕЛЬНАЯК
ОКРУЖНОСТИ
2.
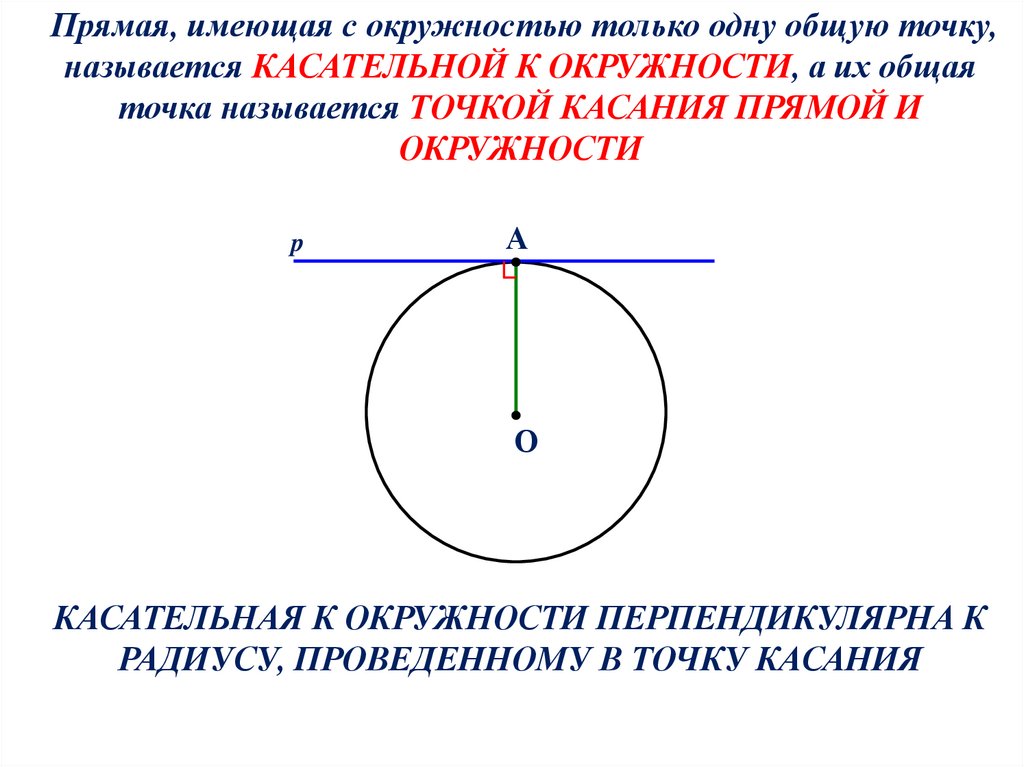
Прямая, имеющая с окружностью только одну общую точку,называется КАСАТЕЛЬНОЙ К ОКРУЖНОСТИ, а их общая
точка называется ТОЧКОЙ КАСАНИЯ ПРЯМОЙ И
ОКРУЖНОСТИ
p
А
О
КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ ПЕРПЕНДИКУЛЯРНА К
РАДИУСУ, ПРОВЕДЕННОМУ В ТОЧКУ КАСАНИЯ
3.
Отрезки AK и AM называются отрезкамикасательных, проведенными из A.
касательная
K точка касания
O
A
M
4.
3B
А
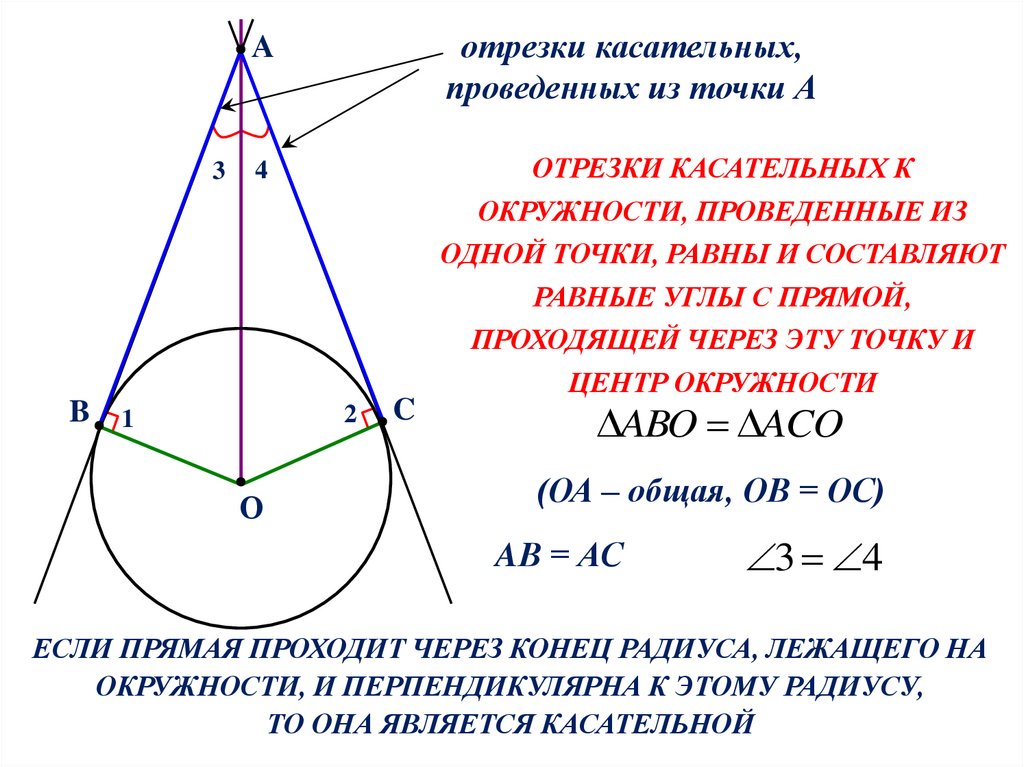
отрезки касательных,
проведенных из точки А
4
ОТРЕЗКИ КАСАТЕЛЬНЫХ К
ОКРУЖНОСТИ, ПРОВЕДЕННЫЕ ИЗ
ОДНОЙ ТОЧКИ, РАВНЫ И СОСТАВЛЯЮТ
РАВНЫЕ УГЛЫ С ПРЯМОЙ,
ПРОХОДЯЩЕЙ ЧЕРЕЗ ЭТУ ТОЧКУ И
ЦЕНТР ОКРУЖНОСТИ
2
1
О
C
ABO ACO
(ОА – общая, ОВ = ОС)
AВ = АС
3 4
ЕСЛИ ПРЯМАЯ ПРОХОДИТ ЧЕРЕЗ КОНЕЦ РАДИУСА, ЛЕЖАЩЕГО НА
ОКРУЖНОСТИ, И ПЕРПЕНДИКУЛЯРНА К ЭТОМУ РАДИУСУ,
ТО ОНА ЯВЛЯЕТСЯ КАСАТЕЛЬНОЙ
5.
Через данную точку А окружности с центром О провестикасательную к этой окружности
p
О
А
6.
Две окружности не имеют общих точек (непересекаются)
7.
Две окружности имеют 2 общие точки(пересекаются)
8.
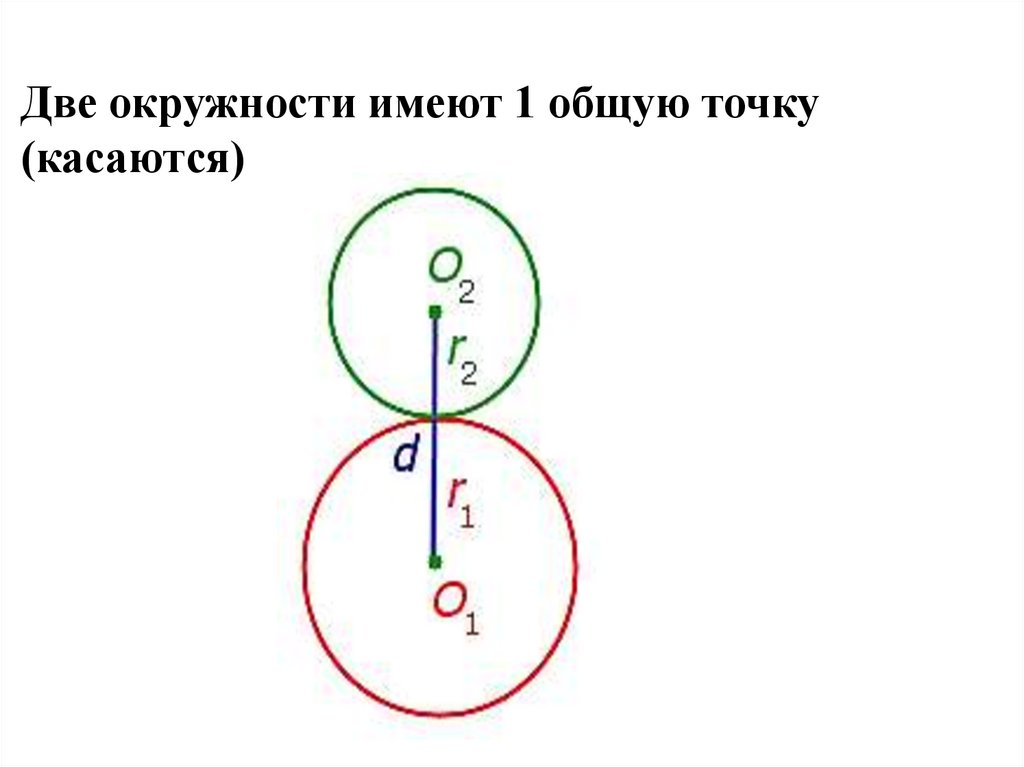
Две окружности имеют 1 общую точку(касаются)
9.
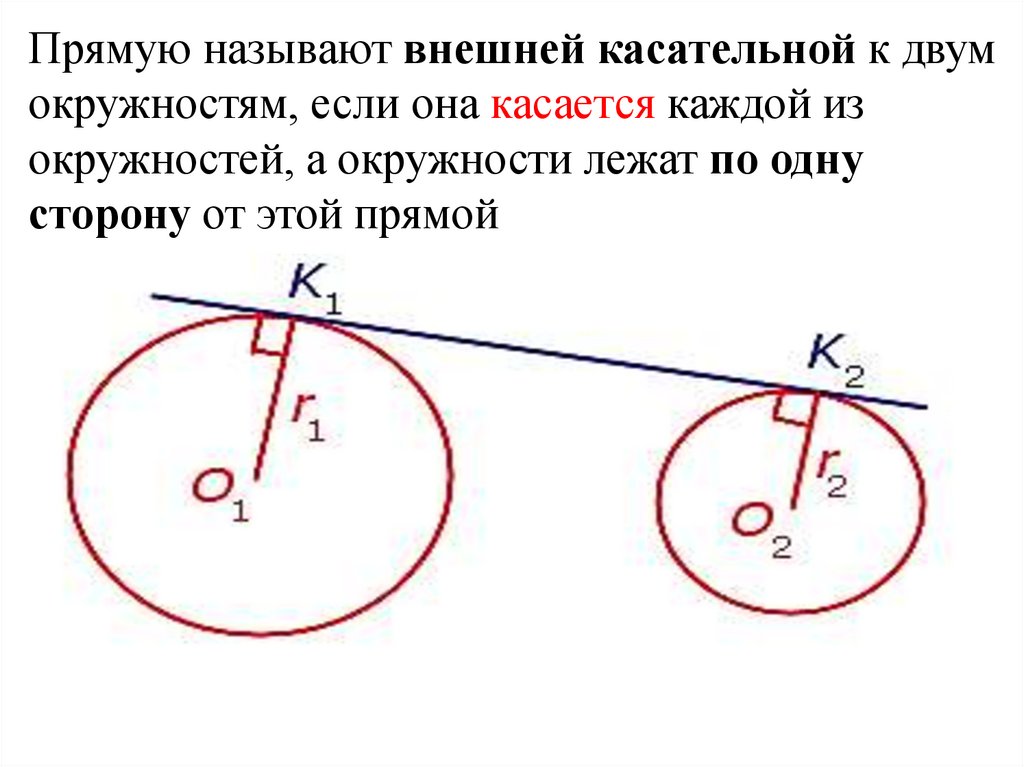
Прямую называют внешней касательной к двумокружностям, если она касается каждой из
окружностей, а окружности лежат по одну
сторону от этой прямой
10.
Прямую называют внутренней касательной кдвум окружностям, если она касается каждой из
окружностей, а окружности лежат по разные
стороны от этой прямой.
11.
Существует единственная общая внешняякасательная. Других общих касательных нет.
12.
Теорема об угле между касательной и хордой:Угол меду касательной и хордой равен
половине дуги, которую стягивает данная
хорда
13.
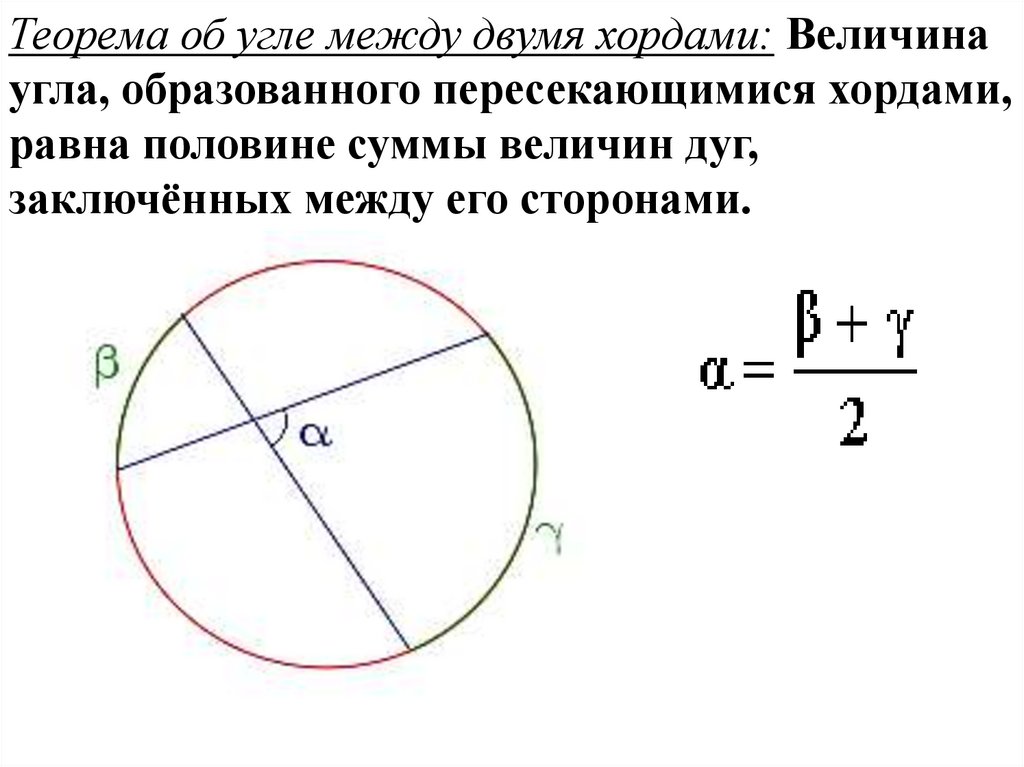
Теорема об угле между двумя хордами: Величинаугла, образованного пересекающимися хордами,
равна половине суммы величин дуг,
заключённых между его сторонами.
14.
Теорема об угле между двумя секущими:Величина угла, образованного секущими,
пересекающимися вне круга, равна половине
разности величин дуг, заключённых между его
сторонами









 Математика
Математика








