Окружность

1. Окружность

2. Содержание

Определение
Касательная
Хорда
Свойства
Вписанная окружность
Описанная окружность
Углы в окружности
Длины и площади

3.

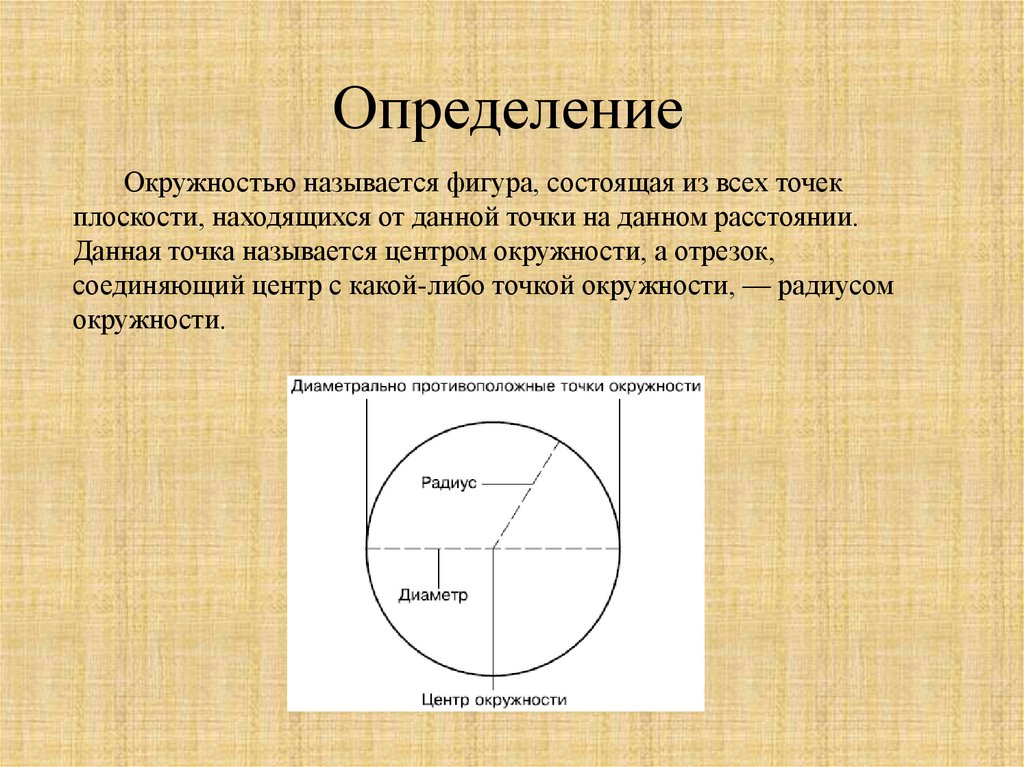
Определение
Окружностью называется фигура, состоящая из всех точек
плоскости, находящихся от данной точки на данном расстоянии.
Данная точка называется центром окружности, а отрезок,
соединяющий центр с какой-либо точкой окружности, — радиусом
окружности.

4. Касательная

Прямая, имеющая с только одну общую точку,
называется касательной к окружности, а их общая
точка называется точкой касания прямой и
окружности.
Свойства касательной:
1. Касательная к окружности перпендикулярна к
радиусу, проведенному в точку касания.
2.Отрезки касательных к окружности, проведенных
из одной точки, равны и составляют равные углы с
прямой, проходящей через эту точку и центр
окружности.

5. Хорда

Отрезок, соединяющий две точки окружности,
называется ее хордой. Хорда, проходящая через центр
окружности, называется диаметром.
Свойства хорд:
1.Диаметр (радиус), перпендикулярный к хорде, делит эту
хорду и обе стягиваемые ею дуги пополам. Верна и
обратная теорема: если диаметр (радиус) делит пополам
хорду, то он перпендикулярен этой хорде.
2.Дуги, заключенные между параллельными хордами,
равны.
3.Если две хорды окружности, AB и CD пересекаются в
точке M, то произведение отрезков одной хорды равно
произведению отрезков другой хорды: AM•MB = CM•MD.

6. Свойства

1.Прямая может не иметь с окружностью общих точек;
иметь с окружностью одну общую точку (касательная);
иметь с ней две общие точки (секущая).
2.Через три точки, не лежащие на одной прямой, можно
провести окружность, и притом только одну.
2.Точка касания двух окружностей лежит на линии,
соединяющей их центры.

7. Вписанная окружность

Окружность называется вписанной в угол, если она лежит
внутри угла и касается его сторон. Центр окружности,
вписанной в угол, лежит на биссектрисе этого угла.
Окружность называется вписанной в выпуклый
многоугольник, если она лежит внутри данного
многоугольника и касается всех прямых, проходящих через
его стороны. В выпуклый многоугольник можно вписать не
более одной окружности. Сам многоугольник в таком случае
называется описанным около данной окружности.

8. Вписанная окружность в многоугольнике

Если в данный выпуклый многоугольник можно
вписать окружность, то биссектрисы всех углов
данного многоугольника пересекаются в одной
точке, которая является центром вписанной
окружности.
Радиус вписанной в многоугольник окружности
равен отношению его площади к полупериметру[1]
Теорема о трезубце: Если W — точка пересечения
биссектрисы угла A с описанной окружностью, а I —
центр вписанной окружности, то | WI | = | WB | = |
WC | . Здесь C и B — вершины многоугольника,
соседние с вершиной A.

9. Вписанная окружность в треугольнике

1.Центр O вписанной окружности называется
инцентром, он равноудалён от всех сторон и является
точкой пересечения биссектрис треугольника.
2.Радиус вписанной в треугольник окружности
равен
3.Если прямая, проходящая через точку О параллельно стороне AB,
пересекает стороны BC и CA в точках A1 и B1, то A1B1 = A1B + AB1.
4. Радиус вписанной в прямоугольный треугольник с катетами a, b и
гипотенузой c окружности равен
5.Расстояние от вершины С треугольника до точки, в которой вписанная
окружность касается стороны равно

10. Вписанная окружность для четырёхугольника

1.Описанный четырёхугольник, если у него нет самопересечений
(«простой»), должен быть выпуклым.
2.В выпуклый четырёхугольник ABCD можно вписать
окружность тогда и только тогда, когда суммы его
противоположных сторон равны: AB + CD = BC + AD.
3.В параллелограмм можно вписать окружность тогда и только
тогда, когда он является ромбом.
4.Во всяком описанном четырёхугольнике середины диагоналей
и центр вписанной окружности лежат на одной прямой (теорема
Ньютона).

11. Описанная окружность

Центр описанной окружности выпуклого n-угольника лежит в
точке пересечения серединных перпендикуляров к его
сторонам. Как следствие: если рядом с n-угольником описана
окружность, то все серединные перпендикуляры к его
сторонам пересекаются в одной точке (центре окружности).
Вокруг любого правильного многоугольника можно описать
окружность.

12. Описанная окружность для треугольника

1.Центр описанной окружности — точка пересечения серединных
перпендикуляров, ее радиус R вычисляется по формуле:
R=
R=
,
;
здесь a, b, c — стороны треугольника, — угол, лежащий против
стороны a, S — площадь треугольника;
2.Центр описанной около прямоугольного треугольника
окружности лежит на середине гипотенузы;
3.Центр описанной и вписанной окружностей треугольника
совпадают только в том случае, когда этот треугольник —
правильный.

13. Описанная окружность в четырёхугольнике

1.Около выпуклого четырехугольника можно
описать окружность тогда и только тогда, когда
сумма его внутренних противоположных углов
равна 180°:
2.Около параллелограмма можно описать окружность тогда и
только тогда, когда он является прямоугольником;
3.Около трапеции можно описать окружность тогда и только тогда,
когда эта трапеция — равнобедренная; центр окружности лежит на
пересечении оси симметрии трапеции с серединным
перпендикуляром к боковой стороне.

14. Углы в окружности

Центральным углом в окружности называется плоский угол с
вершиной в ее центре.
Угол, вершина которого лежит на окружности, а стороны
пересекают эту окружность, называется вписанным углом.
Любые две точки окружности делят ее на две части. Каждая из
этих частей называется дугой окружности. Мерой дуги может
служить мера соответствующего ей центрального угла.
Дуга называется полуокружностью, если отрезок, соединяющий
её концы, является диаметром.
Свойства углов, связанных с окружностью
1.Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.
2.Вписанный угол либо равен половине соответствующего ему центрального угла,
либо дополняет половину этого угла до 180°.
3.Вписанный угол, опирающийся на диаметр, равен 90°.
4.Угол, образованный касательной к окружности и секущей, проведенной через
точку касания, равен половине дуги, заключенной между его сторонами.

15. Длины и площади

Длиной окружности называется предел последовательности периметров
правильных многоугольников, вписанных в данную окружность, при
неограниченном увеличении числа сторон.
1.Длина окружности L вычисляется по формуле L=πd, где d - диаметр окружности,
или по формуле L=2πr, где r - радиус окружности.
2.Длина дуги окружности с угловой величиной в α∘ вычисляется по формуле
l=πrα180
3.Площадь круга радиуса r вычисляется по формуле
S=πr2
4.Площадь сектора с угловой величиной дуги α∘ вычисляется по
формуле Sсект=360πr2α