Компьютерный анализ. Классификация методов исследования

1.

Дисциплина:
Компьютерный анализа

2. План

Классификация методов исследования
Классификация количественных
(статистических) методов
Элементы теории измерений
Описательная статистика
Корреляционный и регрессионный анализ
Проверка гипотез
Факторный и кластерный анализ

3.

Наука начинается там, где есть
измерения ( Д.Менделеев)
Измеряй все доступное
измерению и делай
недоступное измерению –
доступным (Г.Галилей)

4. Классификация методов исследования (по Ананьеву)

Методы
исследования
Организационные
Методы сбора
данных
Методы обработки
данных
Методы интерпретации
данных

5. Организационные методы

Организационные методы
Сравнительный
Лонгитюдный
Комплексный

6. Методы сбора данных

Методы сбора данных
Опрос
Анализ документов
Наблюдение
Эксперимент

7. Методы обработки данных

Методы обработки
данных
Качественные
Количественные

8. Количественные методы

Количественные
(статистические) методы
Описательная статистика
Проверка гипотез
Корреляционный и
регрессионный анализ
Методы многомерного анализа
( факторный, кластерный)

9. Элементы теории измерений

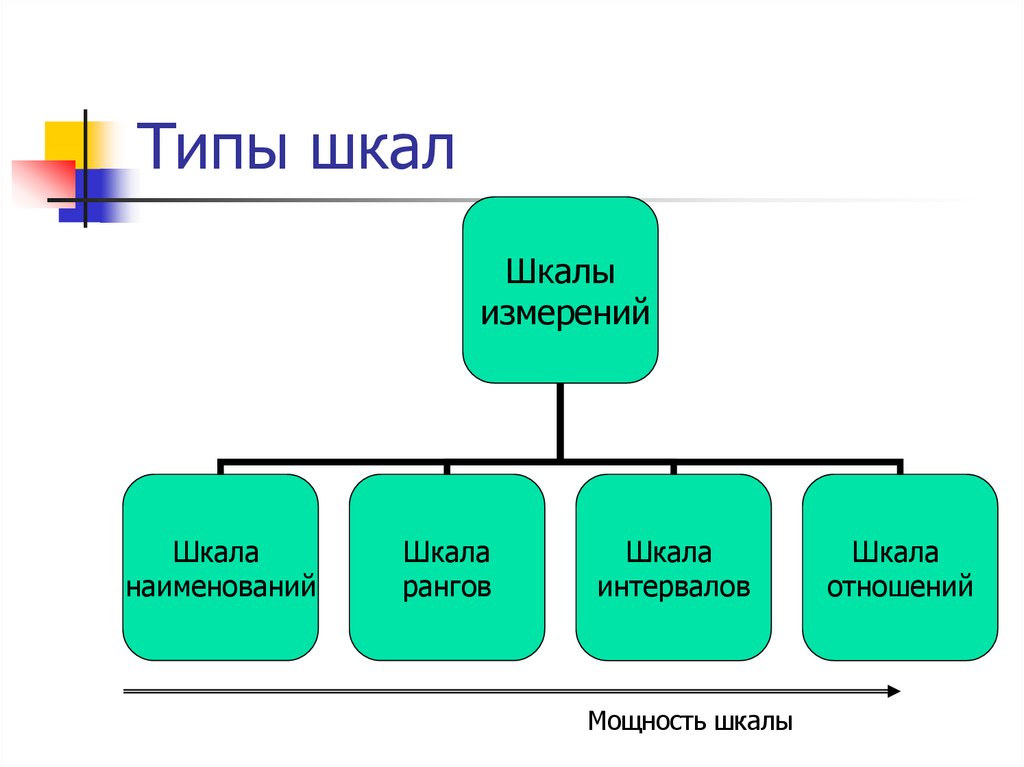
10. Типы шкал

Шкалы
измерений
Шкала
наименований
Шкала
рангов
Шкала
интервалов
Мощность шкалы
Шкала
отношений

11. Номинальная шкала

разделяет все объекты на
непересекающиеся классы;
классы обозначаются номерами;
то, что номер одного класса больше
или меньше номера другого класса,
ничего нам не говорит о свойствах
объектов, кроме того, что они
различаются.

12. Пример номинальной шкалы

Ваше семейное положение:
1. Женат
2. Холост
3. Разведен
4. Вдовец
5. Состою в гражданском браке

13. Пример номинальной шкалы для опроса соучеников Гарри Поттера

Ваш факультет
1) Гриффиндор
2) Слизерин
3) Когтевран
4) Пуффендуй

14. Дихотомическая шкала

Разновидность шкалы номинальной,
которая имеет всего две градации,
например:
1) справился с написанием
диссертации
2) не справился с написанием
диссертации

15. Порядковая(ранговая) шкала

- это шкала, в которой
объекты разделены на классы,
классы обозначены номерами,
но еще и упорядочены по
возрастанию или убыванию
измеряемого признака.

16. Пример ранговой шкалы

Альбус Дамблдор
1) подходит для
занятия вакантной
должности
директора школы
волшебства Хогвартс
2) подходит с
оговорками
3) не подходит

17. Замечания о ранговой (порядковой) шкале

Знания, умения, навыки, уровень
квалификации, - все эти признаки
измеряются ранговыми шкалами.
В ранговой шкале мы не знаем истинного
расстояния между классами. Класс "
подходит для занятий вакантной
должности" и "подходит с оговорками"
могут быть реально ближе к друг другу,
чем "подходит с оговорками" и "не
подходит".

18. В минералогии - шкала твердости минералов Мооса

тальк имеет балл 1,
гипс - 2,
кальций - 3,
флюорит - 4,
апатит - 5,
ортоклаз - 6,
кварц - 7,
топаз - 8,
корунд - 9,
алмаз - 10.

19. Бофортова шкала ветров

штиль
слабый ветер
умеренный ветер
сильный ветер
шторм
ураган

20. В медицине порядковыми шкалами являются

шкала стадий гипертонической
болезни (по Мясникову),
шкала степеней сердечной
недостаточности (по СтражескоВасиленко-Лангу),
шкала степени выраженности
коронарной недостаточности (по
Фогельсону)

21.

заболевание не обнаружено;
первая стадия заболевания;
вторая стадия;
третья стадия…

22. В квалиметрии (оценке качества продукции)

имеются критические дефекты
(делающие невозможным
использование)
есть значительные дефекты
присутствуют только незначительные
дефекты
нет дефектов.

23. Интервальная шкала

В интервальной шкале существует
единица измерения, с помощью которой
объекты можно классифицировать,
упорядочить, и приписать им числа так,
чтобы классы отстояли друг от друга на
равном расстоянии.
Точка 0 на такой шкале произвольна и не
говорит об отсутствии свойства, которое
измеряется.
Примеры шкал: шкала календарного
времени и шкала температур (по
Цельсию).

24. Пример интервальной шкалы

Комфортная температура в
компьютерном классе 2-15 во время
вычислительной практики
1) 10-15 градусов
2) 15-20 градусов
3) 20-25 градусов

25. Шкала отношений

Шкала отношений определяется как
интервальная, однако точка 0 на
такой шкале свидетельствует об
отсутствии измеряемого свойства.
Примеры: время выполнения
задания, число ошибок, число
правильно решенных задач, доход,
цена, вес…

26. Описательная статистика предназначена для компактного описания имеющихся данных

Шкалы для измерения данных
Табулирование данных
Графическое представление (гистограммы,
полигоны, кумулятивные кривые)
Вычисление статистических показателей
( абсолютных, относительных, процентных
частот, накопленных частот, процентилей,
мер центральной тенденции,
мер изменчивости, асимметрии, эксцесса,
определение формы распределения
измеряемых величин)

27. Задача на описательную статистику

В связи с вхождением в Болонский процесс
администрацию школы чародейства и волшебства
Хогвартс интересует информация о предметах,
выбранных учениками в качестве «экзамена по
выбору».
В результате опроса было установлено, что
«зельеваренье» выбрали 10 человек,
«трансфигурацию» – 15, «нумерологию» - 3,
«прорицание» - 8, «историю магии» -5.
Постройте частотное распределение для этих
данных, рассчитайте относительные, процентные
и накопленные частоты. Постройте диаграммы и
графики.

28. «Экзамен по выбору» в школе волшебства Хогвартс

Предмет
Число
учеников
Зельеварение
10
Трансфигурация
История магии
Нумерология
15
5
8
Прорицание
Всего
3
41

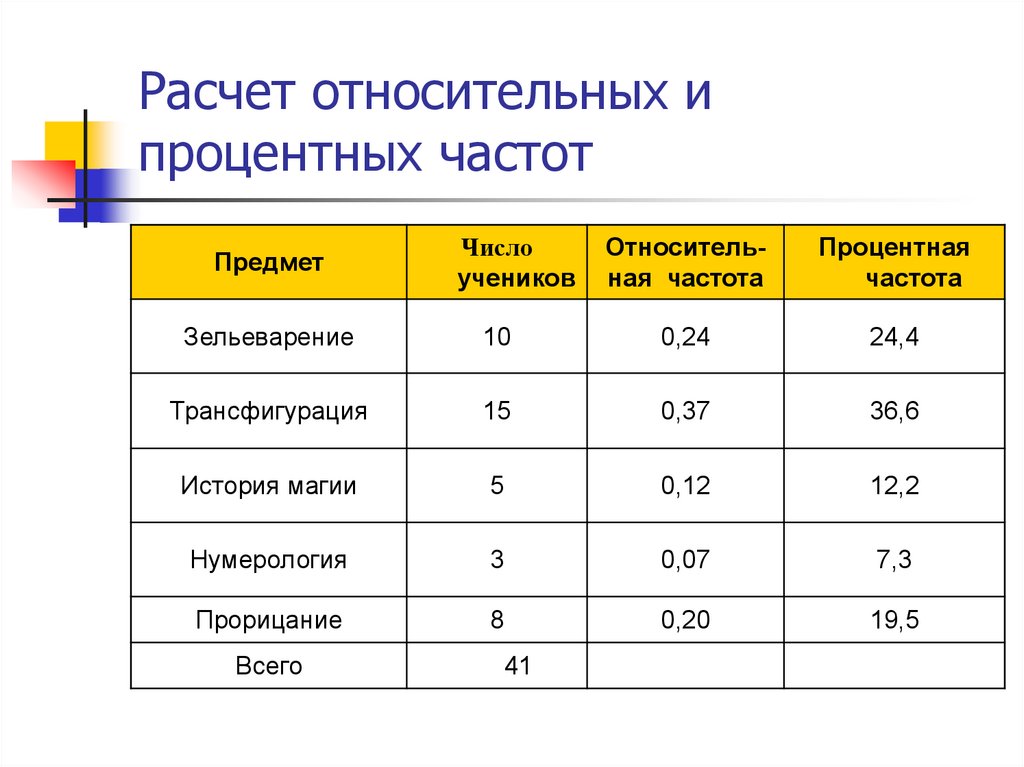
29. Расчет относительных и процентных частот

Предмет
Число
учеников
Относительная частота
Процентная
частота
Зельеварение
10
0,24
24,4
Трансфигурация
15
0,37
36,6
История магии
5
0,12
12,2
Нумерология
3
0,07
7,3
Прорицание
8
0,20
19,5
Всего
41

30. Гистограмма частотного распределения учеников школы волшебства Хогвартс (экзамен по выбору)

40,0
36,6
35,0
24,4
25,0
19,5
20,0
12,2
15,0
7,3
10,0
5,0
предмет
ан
ие
Пр
ор
иц
Ну
м
ер
ол
ог
ия
ма
ги
и
Ис
то
ри
я
иг
ур
ац
ия
Тр
ан
сф
ар
ен
ие
0,0
Зе
ль
ев
% учеников
30,0

31. Меры центральной тенденции

Мода
Медиана
Среднее арифметическое

32. Мода

Мода – это такое значение в
множестве наблюдений, которое
встречается наиболее часто.
В совокупности значений
(2, 6, 6, 8, 9, 9, 9, 10)
модой является 9.

33. Соглашения об использовании моды

В случае, когда все значения в группе встречаются
одинаково часто, принято считать, что группа оценок не
имеет моды. Т.о. в группе (0,5; 0,5; 1,6; 1,6; 3,9; 3,9) моды
нет.
Когда два соседних значения имеют одинаковую частоту и
они больше частоты любого другого значения, мода есть
среднее этих двух значений. Итак, мода группы значений (0,
1, 1, 2, 2, 2, 3, 3, 3, 4) равна 2,5.
Если два несмежных значения в группе имеют равные
частоты и они больше частот любого значения, то
существует две моды. В группе значений (10, 11, 11, 11, 12,
13, 14, 14, 14, 17) модами являются 11 и 14; в таком случае
говорят, что группа является бимодальной.

34. Медиана

Это значение, которое делит упорядоченное
множество данных пополам, так, что одна
половина значений оказывается больше медианы,
а другая – меньше.
Если данные содержат нечетное число различных
значений, например, 11, 13, 18, 19, 20, то
медиана есть центральное значение, когда они
упорядочены, т.е. Md=18.
Если данные содержат четное число различных
значений, например, 4, 9, 13, 14, то медиана есть
точка, лежащая посередине между двумя
центральными значениями, когда они
упорядочены: Md=(9+13)/2=11.

35. Среднее арифметическое

Среднее
совокупности n
значений
определяется как
или

36. Выбор меры центральной тенденции

При выборе меры необходимо учитывать следующее:
В малых группах мода может быть совершенно
нестабильной
На медиану не влияют величины "больших" и "малых"
значений.
На величину среднего влияет каждое значение.
Некоторые множества данных просто "не имеют
центральной тенденции", что часто вводит в заблуждение
при вычислении только одной меры центральной тенденции.
Особенно это справедливо для групп, имеющих более чем
одну моду.
Центральная тенденция группы данных, содержащих
крайние значения, возможно наилучшим образом
измеряется медианой, когда гистограмма унимодальна.

37. Меры изменчивости

Размах
Дисперсия
Стандартное отклонение

38. Вариационный размах

Размах – это разность максимального и
минимального значений в группе.
Например: размах, значений
0, 2, 3, 5, 8 равен 8-0=8.
Размах не учитывает распределения всех
значений, помимо максимального и
минимального.
Размах является довольно грубой, но
общераспространенной мерой
изменчивости.

39. Дисперсия

40. Стандартное отклонение

Мерой изменчивости, тесно
связанной с дисперсией, является
стандартное отклонение.
Стандартное отклонение,
обозначаемое s, определяется как
положительное значение квадратного
корня из дисперсии.

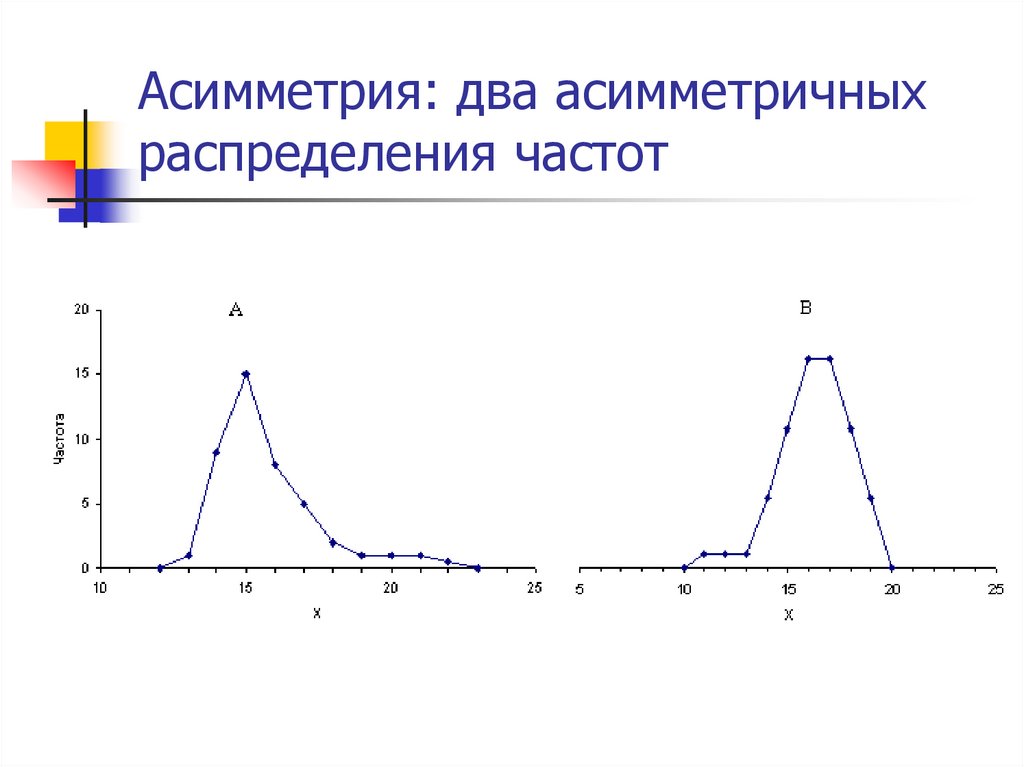
41. Асимметрия: два асимметричных распределения частот

42. Формула для асимметрии

43. Эксцесс

Иногда важно получить
представление о том, являются ли
полигон частот или гистограмма
островершинными или плоскими.
Эксцесс – это греческое слово,
обозначающее свойство
"остроконечности" кривой .

44. Островершинная, плосковершинная и средневершинная кривая распределения частот

45. Формула для эксцесса

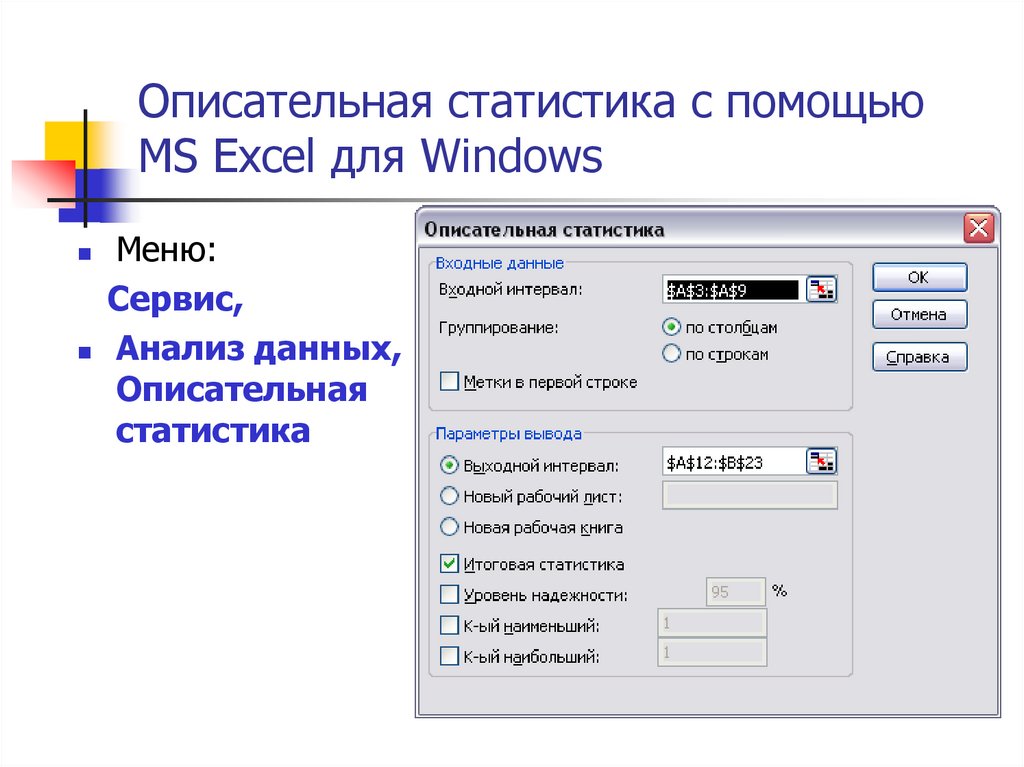
46. Описательная статистика с помощью MS Excel для Windows

Меню:
Сервис,
Анализ данных,
Описательная
статистика

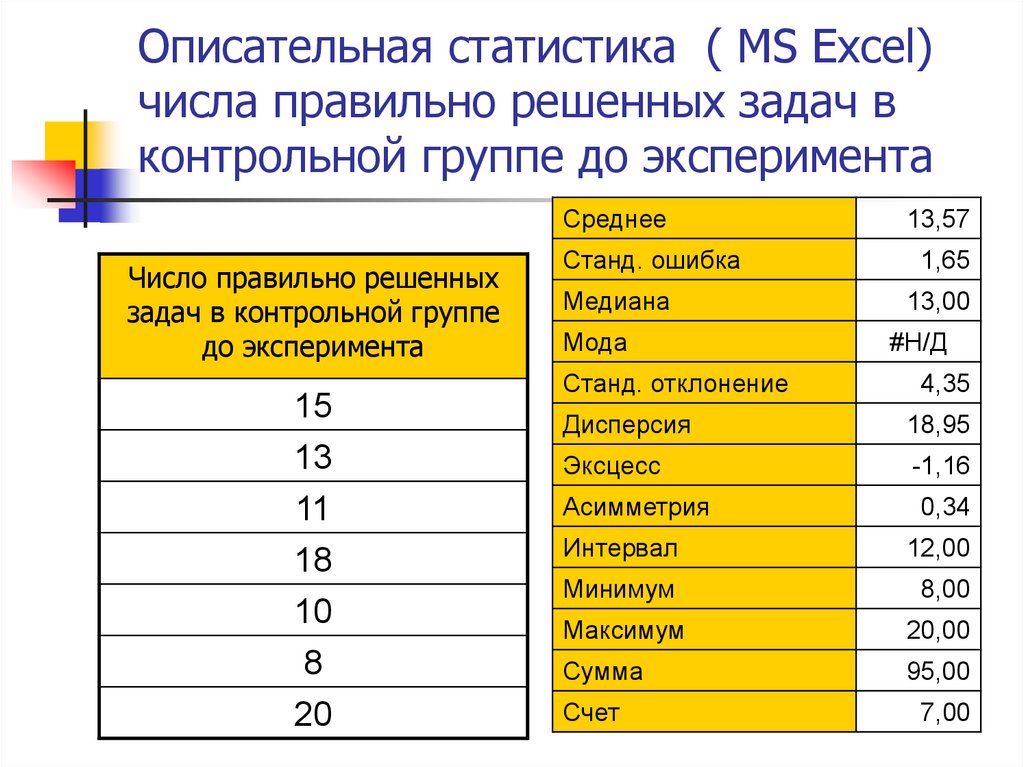
47. Описательная статистика ( MS Excel) числа правильно решенных задач в контрольной группе до эксперимента

Число правильно решенных
задач в контрольной группе
до эксперимента
Среднее
13,57
Станд. ошибка
1,65
Медиана
13,00
Мода
#Н/Д
Станд. отклонение
4,35
Дисперсия
18,95
Эксцесс
-1,16
11
18
10
Асимметрия
0,34
Интервал
12,00
Минимум
8,00
Максимум
20,00
8
20
Сумма
95,00
Счет
7,00
15
13

48. Корреляционный анализ

Используется тогда, когда цель
исследования состоит в обнаружении или
доказательстве связи между двумя или
более переменными, наблюдающимися у
всех членов выборки.
Задача корреляционного анализа
установление корреляционной зависимости
между переменными и определение
величины этой зависимости в виде
коэффициентов корреляции.

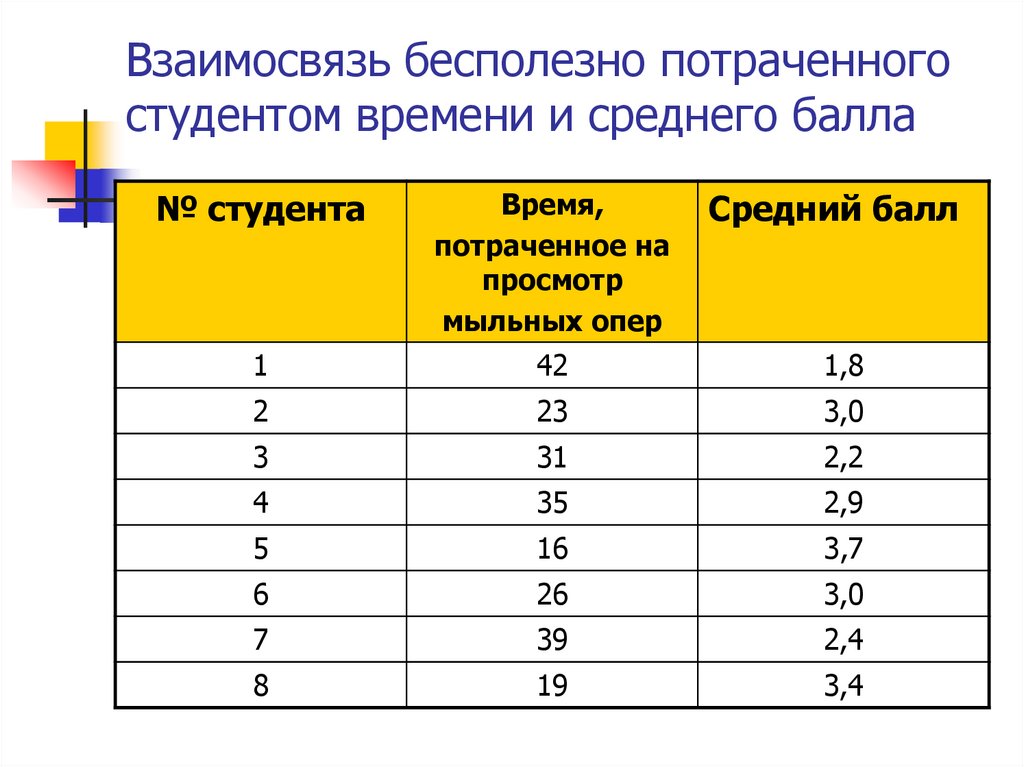
49. Взаимосвязь бесполезно потраченного студентом времени и среднего балла

№ студента
Время,
потраченное на
просмотр
мыльных опер
Средний балл
1
42
1,8
2
23
3,0
3
31
2,2
4
35
2,9
5
16
3,7
6
26
3,0
7
39
2,4
8
19
3,4

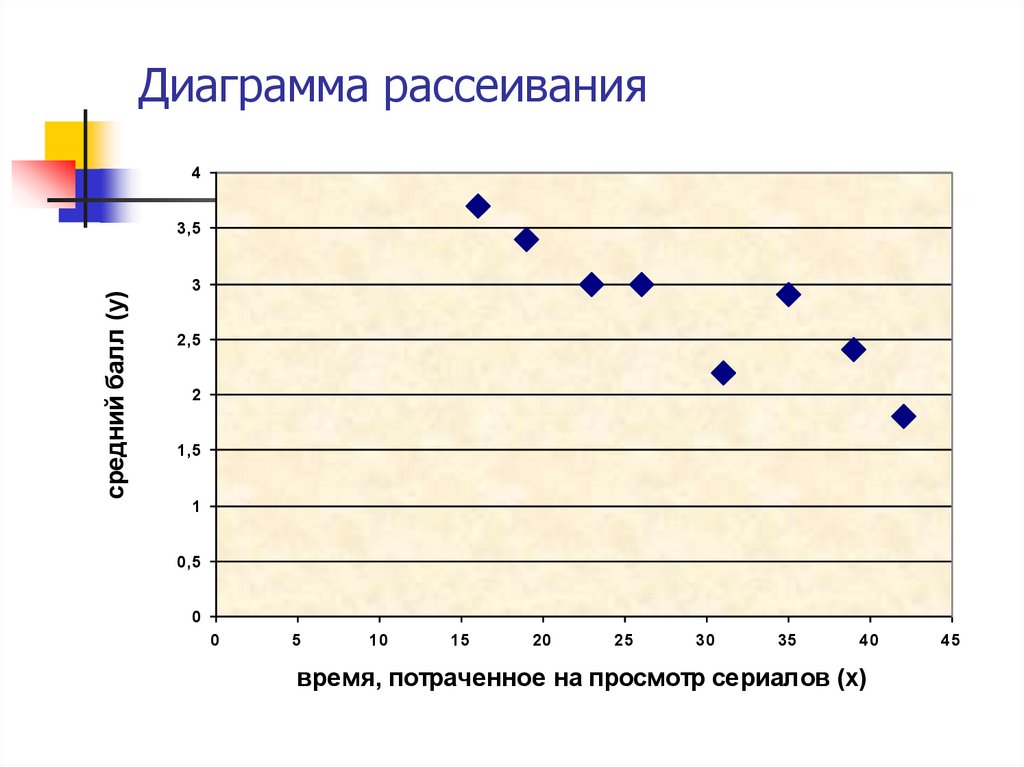
50. Диаграмма рассеивания

4
средний балл (y)
3,5
3
2,5
2
1,5
1
0,5
0
0
5
10
15
20
25
30
35
40
время, потраченное на просмотр сериалов (х)
45

51. Схематическое представление силы и направления корреляции

Полная +
Полная -
Сильная +
Отсутствие
Сильная -

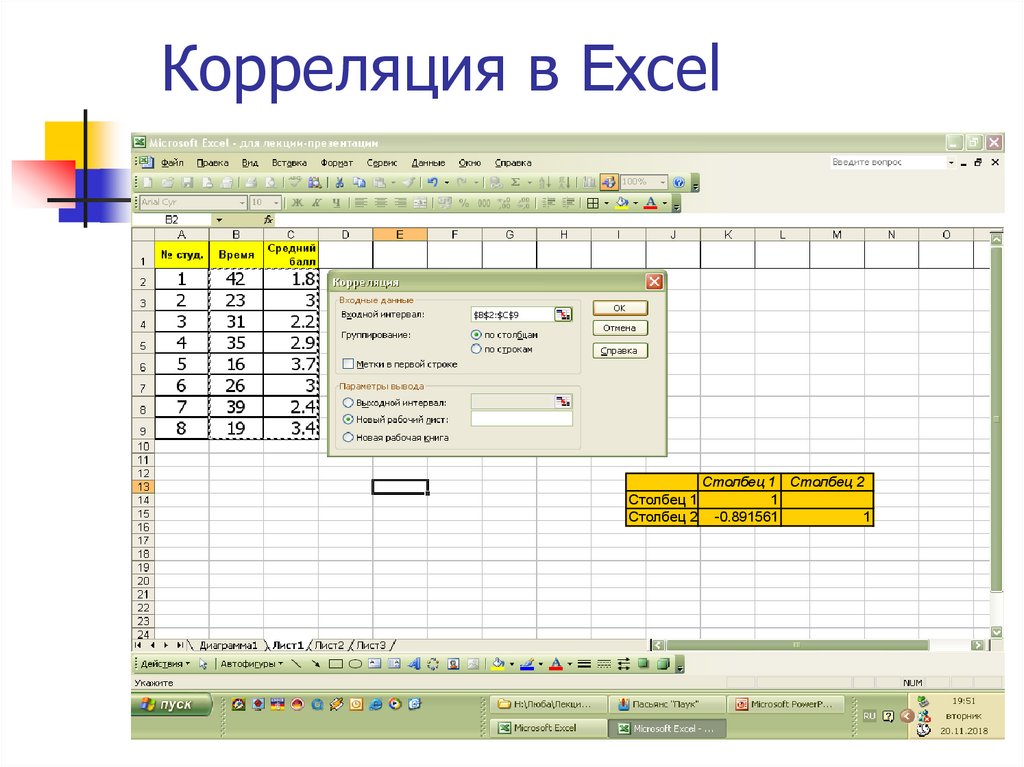
52. Корреляция в Excel

Столбец 1
Столбец 2
Столбец 1 Столбец 2
1
-0.891561
1

53. Регрессионный анализ

Задача регрессионного анализа выражение
корреляционной зависимости в виде
функциональных отношений.
Имея функциональное отношение связи
между переменными можно оценивать У
по Х.
Переменная, которую мы хотим оценить
называется зависимой переменной У, а
переменная используемая для ее оценки независимой переменной или фактором Х.

54. Диаграмма рассеивания, линия предсказания, уравнение регрессии

4
средний балл (y)
3,5
3
2,5
2
y = - 0,0596x + 4,5199
1,5
R2 = 0,7949
1
0,5
0
0
5
10
15
20
25
30
35
40
время, потраченное на просмотр сериалов (х)
45

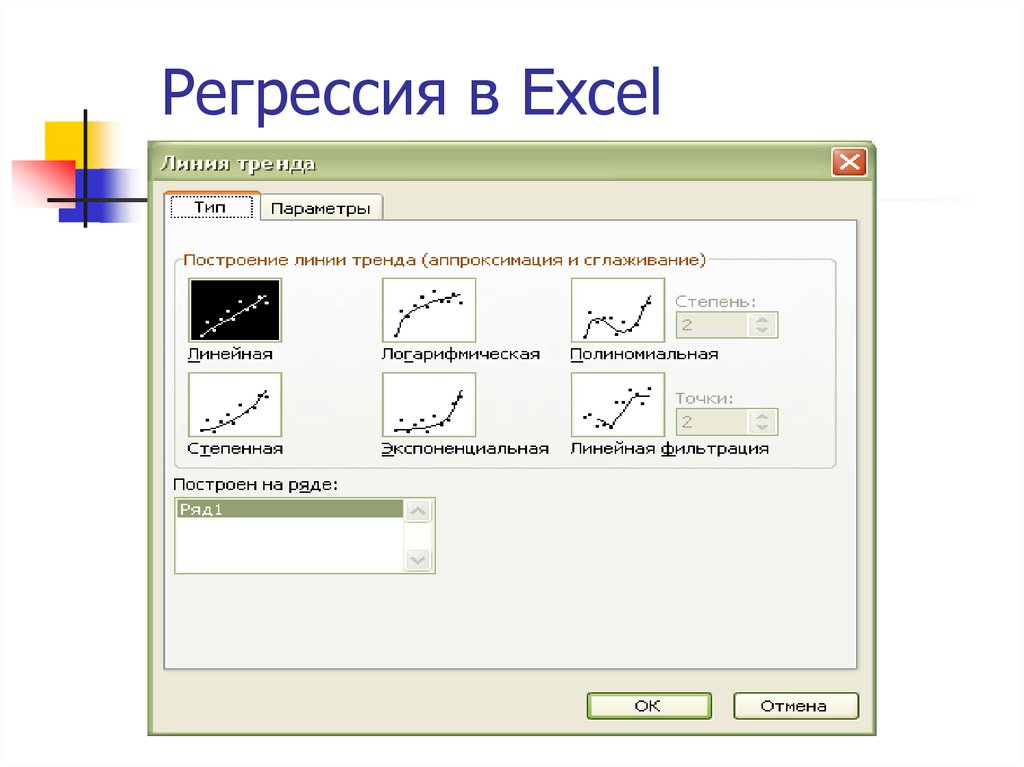
55. Регрессия в Excel

56. Сервис, Анализ данных, Регрессия

57. Проверка гипотез ( теория статистического вывода)

Проверка гипотез, состоит в том, что
исследователь заранее формулирует
некоторое утверждение о параметрах
генеральной совокупности,
затем оценивает степень соответствия
результатов, полученных в выборочном
исследовании, сформулированной гипотезе
и принимает решение об истинности или
ложности гипотезы.

58. Статистические гипотезы разделяются на

Нулевая
гипотеза - это
гипотеза об
отсутствии
различий
Она обозначается
как Но.
Альтернативная
гипотеза - это
гипотеза о
значимости
различий.
Она обозначается
как H1.

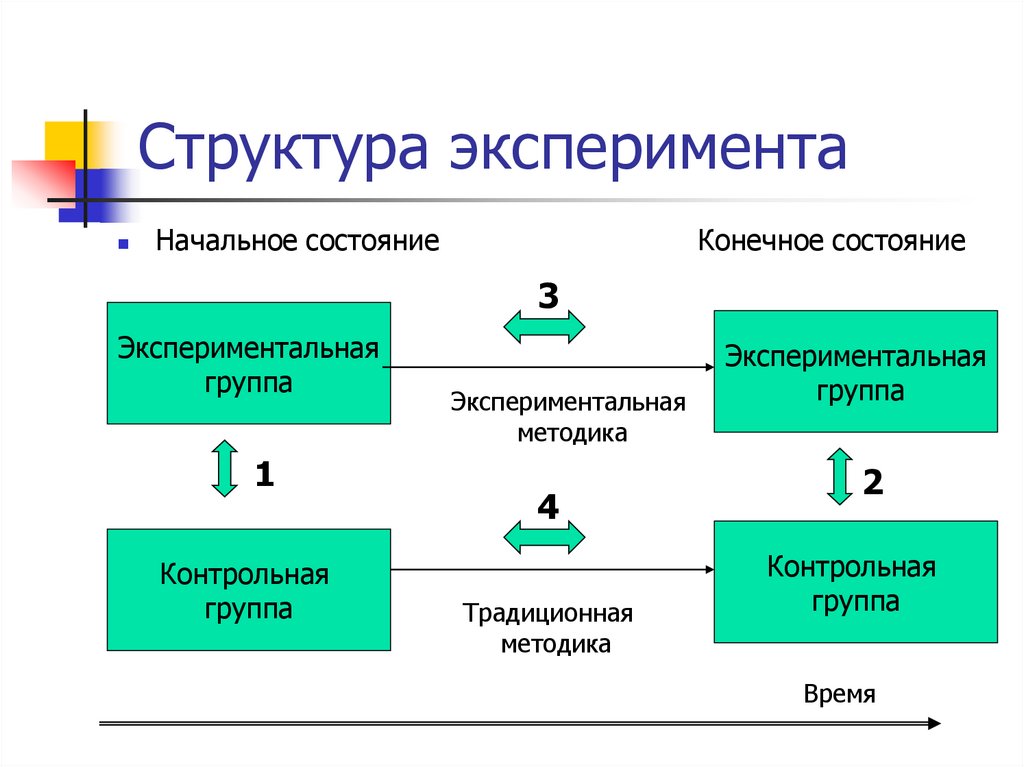
59. Структура эксперимента

Начальное состояние
Конечное состояние
3
Экспериментальная
группа
1
Контрольная
группа
Экспериментальная
методика
4
Традиционная
методика
Экспериментальная
группа
2
Контрольная
группа
Время

60. Алгоритм действия исследователя

На основании сравнения 1 показать
отсутствие статистически значимого
различия между группами до эксперимента
Реализовать воздействие на
экспериментальную группу
На основании сравнения 2 установить
статистически значимое различие между
группами после эксперимента

61. Алгоритм проверки гипотез

1.Формулирование нулевой и
альтернативной гипотезы
2. Выбор подходящего статисти-
ческого критерия, назовем его К.
3. Расчет по данным выборки
H0 : Не существует зависимости
между количеством времени,
бесполезно потраченным студентом,
и его средним баллом
Коэффициент корреляции Пирсона-Браве
rэмп= - 0,89
эмпирического значения Кэмп
4. На основании объема выборки,
уровня значимости, числа степеней
свободы определение критического
значения критерия Kкрит из таблиц
n=8, =0,05
rкрит= 0,707
5. Сопоставление эмпирического и
критического значений критерия:
Если Kэмп>Kкрит,то Ho отвергается.
rэмп > rкрит
Нo отвергается

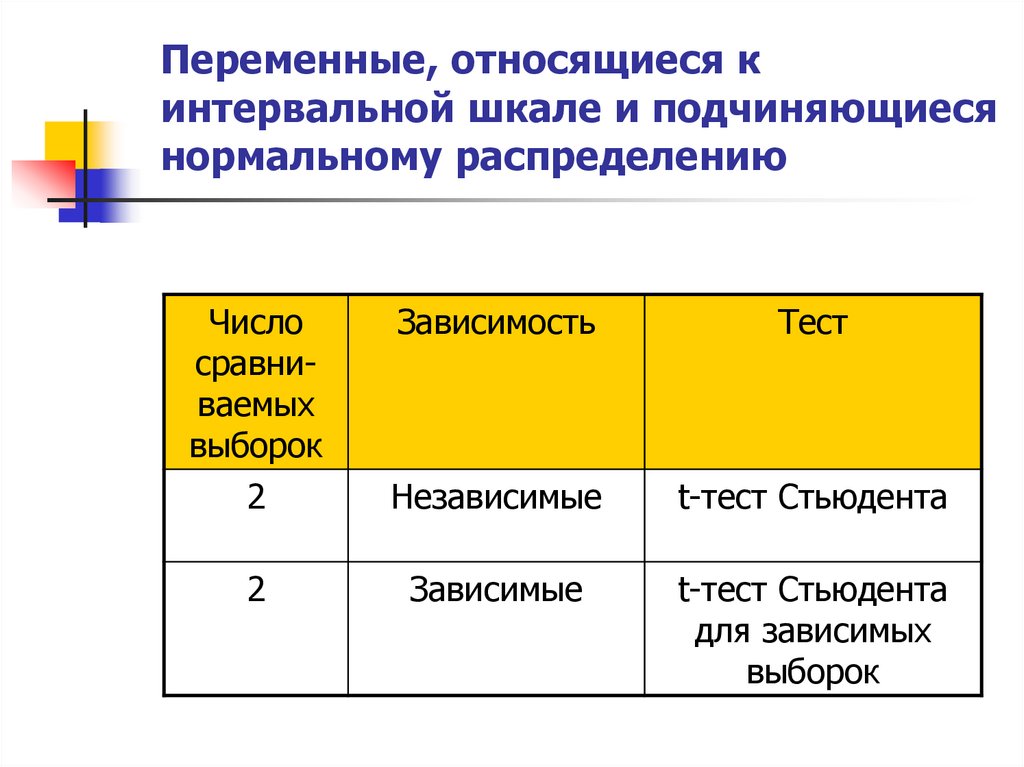
62. Переменные, относящиеся к интервальной шкале и подчиняющиеся нормальному распределению

Число
сравниваемых
выборок
2
Зависимость
Тест
Независимые
t-тест Стьюдента
2
Зависимые
t-тест Стьюдента
для зависимых
выборок

63. Для зависимых выборок

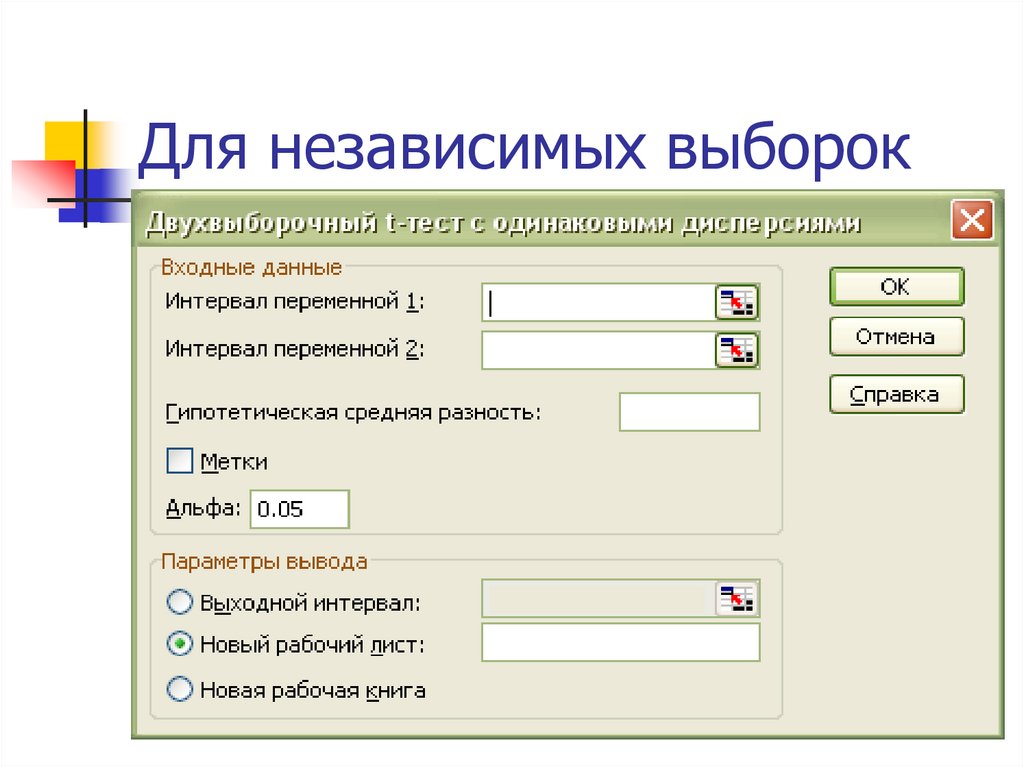
64. Для независимых выборок

65. Цели факторного анализа

сокращение числа переменных (редукция
данных)
определение структуры взаимосвязей
между переменными, т.е. классификация
переменных.
Поэтому факторный анализ используется
или как метод сокращения данных или как
метод классификации.

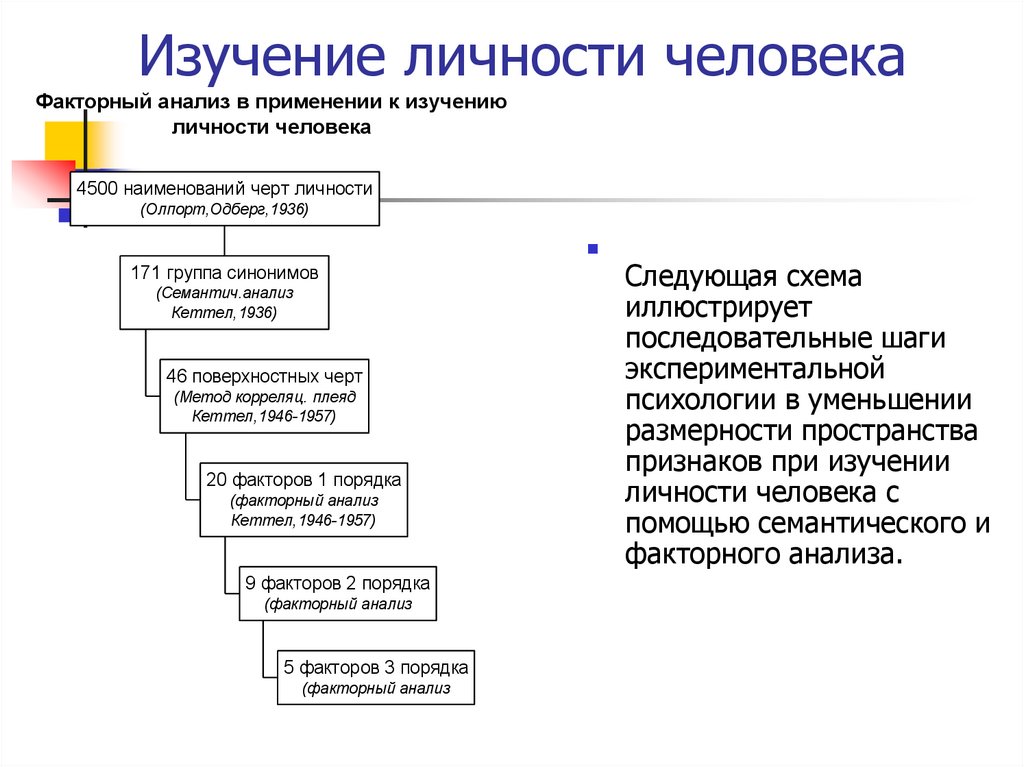
66. Изучение личности человека

Факторный анализ в применении к изучению
личности человека
4500 наименований черт личности
(Олпорт,Одберг,1936)
171 группа синонимов
(Семантич.анализ
Кеттел,1936)
46 поверхностных черт
(Метод корреляц. плеяд
Кеттел,1946-1957)
20 факторов 1 порядка
(факторный анализ
Кеттел,1946-1957)
9 факторов 2 порядка
(факторный анализ
5 факторов 3 порядка
(факторный анализ
Следующая схема
иллюстрирует
последовательные шаги
экспериментальной
психологии в уменьшении
размерности пространства
признаков при изучении
личности человека с
помощью семантического и
факторного анализа.

67. 18 факторов 1 порядка

1.
2.
3.
4.
5.
6.
7.
8.
9.
Тревожность
Раздражительность
Ипохондрия
Шизоидность
Паранойяльность
Подозрительность
Фобии( страхи)
Гипотимия
(подавленность)
Интропсихическая
неупорядоченость
Конфликты узкого круга
11. Независимость
12. Расторможенность
13. Совестливость
14. Общительность
15. Робость, стеснительность
16. Активность, стеничность
17. Эстетическая
впечатлительность
18. Женственность
10.

68. 6 факторов 2 порядка

После применения факторного анализа выявлено 6
факторов 2 порядка.
1-й фактор типичен для неврастенических
состояний (невротизм)
2-й - симптомы психических расстройств
3-й - снижение настроения (депрессия)
4-й - асоциальность
5-й - интроверсия (социально контактная
личность)
6-й - интерес к духовным ценностям, мягкость,
доброта (сензитивность)

69. Кластерный анализ

Другим направлением конденсации
информации является кластерный анализ
(таксономия, автоклассификация,
распознавание образов).
Аналогично факторному анализу задачей
кластерного анализа является такое
представление многомерного массива
информации в сжатом виде, чтобы потеря
информации не была чрезмерной.
Он позволяет объединить множество
объектов в небольшое число однородных
групп, называемых кластерами.

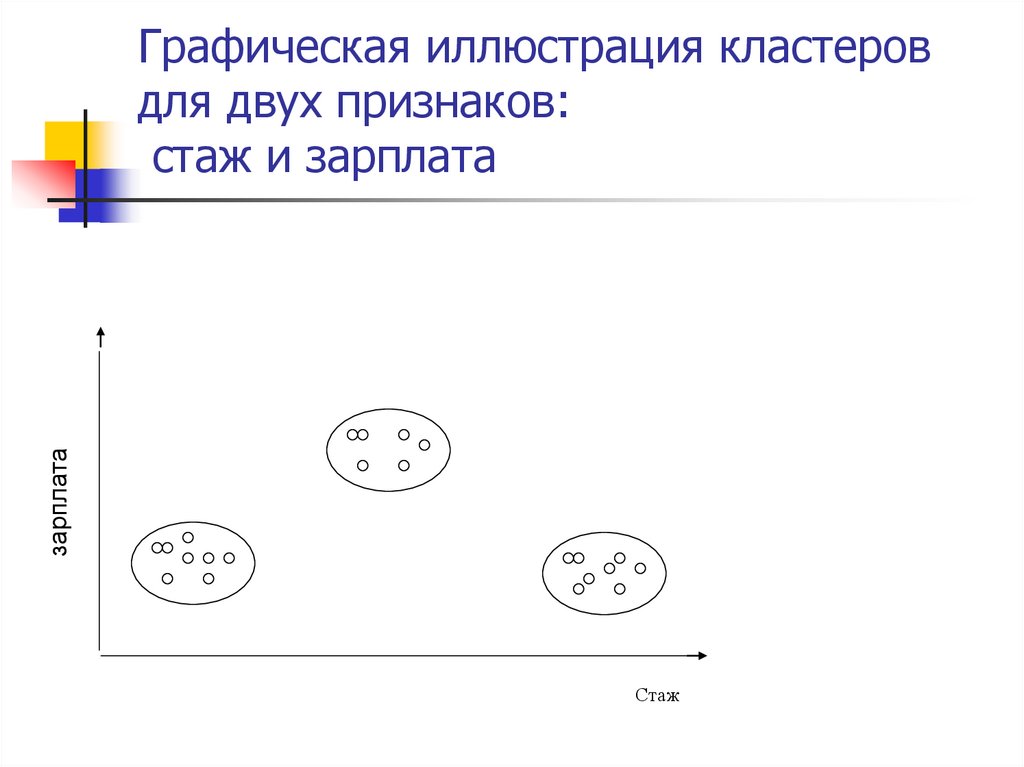
70. Графическая иллюстрация кластеров для двух признаков: стаж и зарплата

зарплата
Графическая иллюстрация кластеров
для двух признаков:
стаж и зарплата
Стаж

71. Компьютерные программы для статистических вычислений

Мicrosoft Excel
Statistica (www.statsoft.ru)
SPSS для Windows (www.spss.com)

72. Заключение

Элиота Аронсона, выдающегося социального психолога
спросили, что помогает ему в исследованиях.
- «Три вещи.
Во-первых я страстно интересуюсь
поведением людей в обществе,
во-вторых, мне нравится делать
открытия, способные улучшить жизнь
людей,
и наконец, сам процесс исследования
– это большое удовольствие».