Статистические методы обработки информации в научных исследованиях

1. Статистические методы обработки информации в научных исследованиях

К.м.н., доцент Рычкова Т.А.,
К.м.н., доцент Таловерова Л.И.

2.

«В жизни, как правило,
преуспевает тот, кто
располагает лучшей
информацией»
Б.Дизраэли

3. План:

1. Основные понятия статистического
исследования.
2. Правила сбора и оформления данных
для статобработки.
3. Выбор статистического метода
исследования.
4. Анализ результатов статобработки
данных и формулировка выводов.

4.

4
Стати́стика — отрасль знаний, в которой
излагаются общие вопросы:
сбора,
измерения,
анализа данных.
Слово «статистика» происходит от
латинского status — состояние дел.
В науку термин «статистика» ввёл
немецкий ученый Готфрид Ахенвалль в
1746 году.

5.

Статистика есть наука о том,
как, не умея мыслить и понимать,
заставить делать это цифры
Василий Осипович
Ключевский

6. 4 основных задачи статистики

1. статистическое описание выборки
2. сравнение параметров двух и более
выборок
3. определение связей между
параметрами
4. динамический анализ (временной
анализ изменения статистических
параметров выборки)

7.

Этапы статистического
исследования
I. Составление плана
статистического исследования,
разработка программы
II. Регистрация и сбор
статистического материала

8.

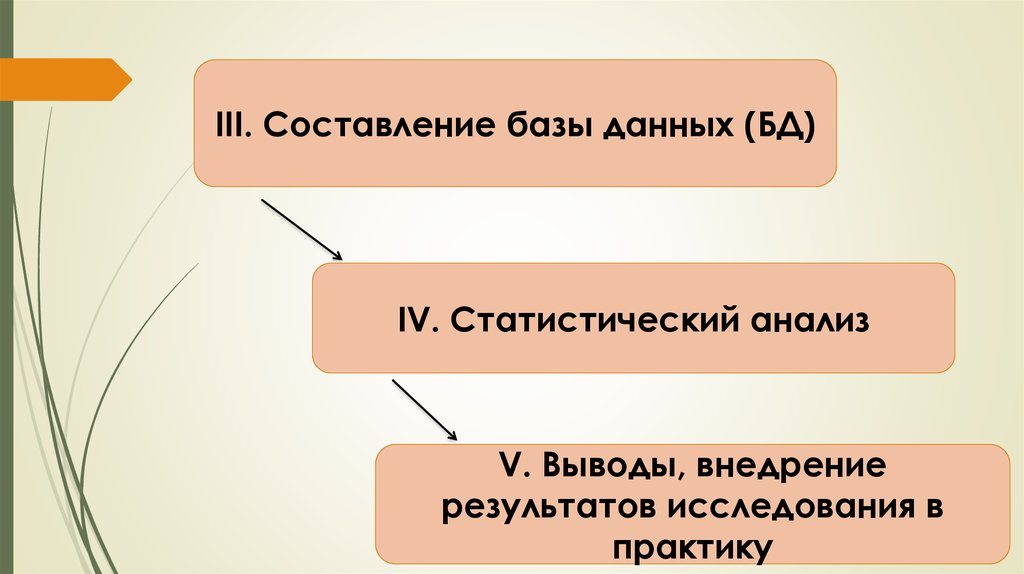
III. Составление базы данных (БД)
IV. Статистический анализ
V. Выводы, внедрение
результатов исследования в
практику

9.

10. Обработать статистическими методами можно лишь то, что поддается измерению Измерение – присвоение объекту (явлению, событию,

процессу и т.п.) числа (значения)
по определенному правилу
Признак – измеренное свойство объекта
наблюдения

11. Данные

Даты
Количественные
данные
Качественные
данные
Дискретные
Непрерывные
Целые - дети
Рост, Вес, t, АД
Интервальные,
абсолютные
Номинальные
Порядковые
Коды групп
Шкалы, оценки,
Относительные, %
стадии

12. Характеристика данных

Количественные дискретные признаки измеряются
целыми числовыми значениями (например, кол-во детей,
беременностей)
Количественные непрерывные признаки измеряются
любыми числовыми значениями (например, возраст,
рост, вес, давление).
Качественные признаки – характеризуют некоторое
состояние объекта, но не могут быть измерены
количественно (например, пол, профессия, диагноз).
Порядковые признаки – могут быть измерены в шкалах
(например, школьные оценки, степень тяжести
заболевания – легкая (1), средняя (2), тяжелая (3) и т.д.).

13. Абсолютные величины

Абсолютные величины – отображают
численную величину измеренного явления,
уровень развития явления
Абсолютные величины в статистике:
• являются именованными
• измеряются в конкретных единицах (г, см, кг)

14. Относительные величины

Относительная величина
(относительный показатель,
коэффициент) - это обобщающий
показатель, который дает числовую меру
соотношения двух сопоставляемых
абсолютных величин

15. Данные

Даты
Количественные
данные
Качественные
данные
Дискретные
Непрерывные
Целые - дети
Рост, Вес, t, АД
Интервальные,
абсолютные
Номинальные
Порядковые
Коды групп
Шкалы, оценки,
Относительные, %
стадии

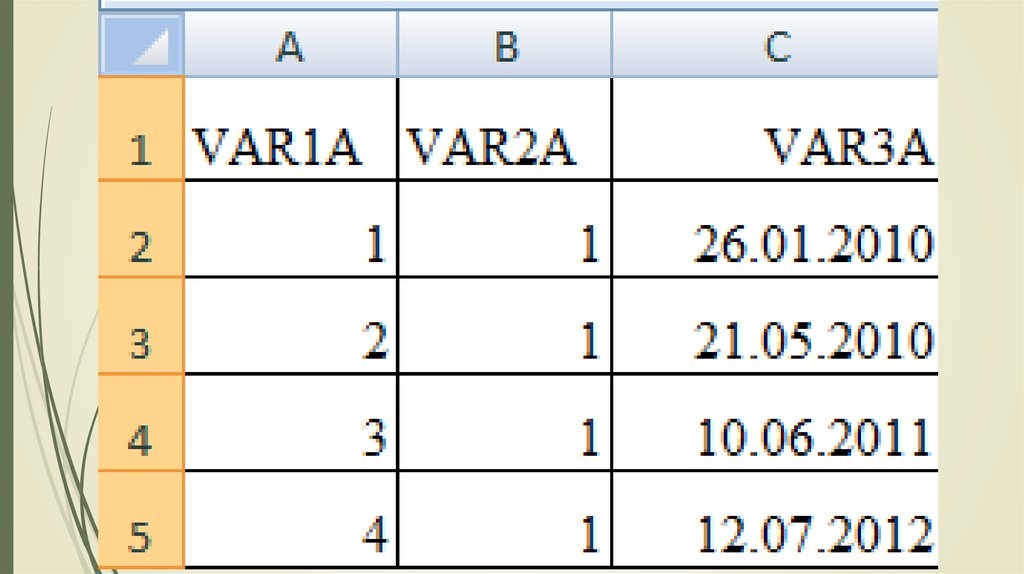
16. Фрагмент БД в MS EXCEL:

17. Описание БД:

Цель исследования:
разработать и экспериментально проверить
эффективность системы коррекционных занятий
по развитию наглядно-образного мышления
детей дошкольного возраста с минимальной
мозговой дисфункцией.

18. Описание БД:

Объект исследования –
наглядно-образное мышление детей дошкольного
возраста с минимальной мозговой дисфункцией.
Предмет исследования –
особенности
развития
наглядно-образного
мышления
детей
дошкольного
возраста
с
минимальной мозговой дисфункцией.

19. Описание БД:

Обследовано:
24 ребенка с ММД и
20 здоровых детей 5-6 лет по 23
признакам. Из них 15 качественных и 8
количественных.

20.

Методы исследования:
тест рисования часов
заучивание и воспроизведение 5 слов
исследование памяти (серийный и
обратный счет, вербальная и невербальная
память, ассоциации)…

21.

Задачи исследования:
1. Установить частоту встречаемости,
выраженность и характер нарушений
________(VAR7-VAR14)…
2. Выявить частоту встречаемости, степень
выраженности и факторы риска
______VAR4A-VAR6A…
3. Выявить взаимосвязь между ______ VAR9AVAR13A…

22. Особенности описания признаков:

Количественные признаки:
VAR1=«возраст, лет»
Качественные признаки:
VAR2A=«пол»
1-девочка
2-мальчик

23.

24. VAR61=«окружность головы, см»

25. Описание признаков:

VAR5А=«тревога, балл» НОРМА: 0-7
VAR6А=«тревога»
1-норма
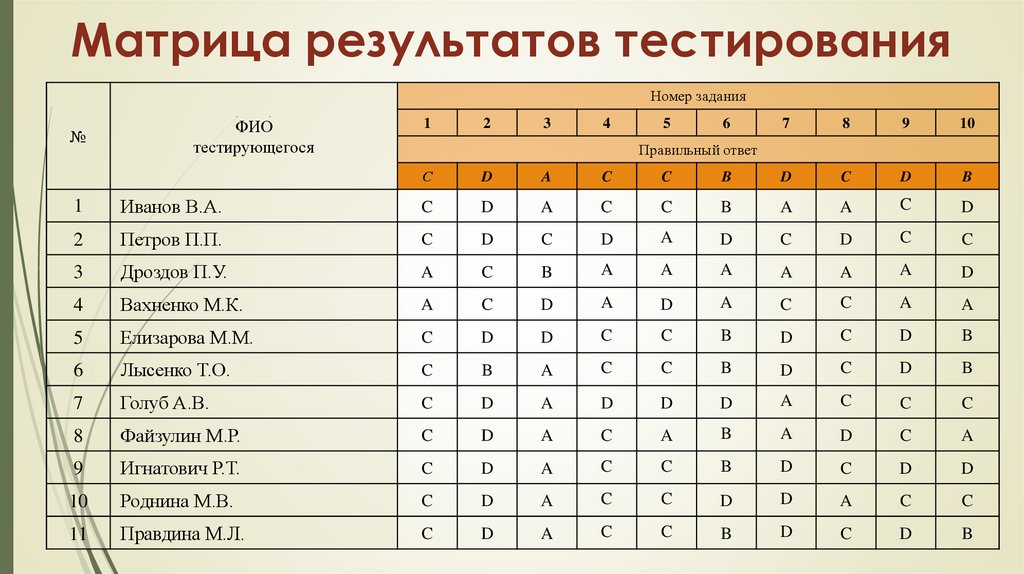
2-не норма

26. Матрица результатов тестирования

Номер задания
№
ФИО
тестирующегося
1
2
3
4
5
6
7
8
9
10
Правильный ответ
С
D
A
C
C
B
D
C
D
B
1
Иванов В.А.
C
D
A
C
C
B
A
A
C
D
2
Петров П.П.
C
D
C
D
A
D
C
D
C
C
3
Дроздов П.У.
A
C
B
A
A
A
A
A
A
D
4
Вахненко М.К.
A
C
D
A
D
A
C
C
A
A
5
Елизарова М.М.
C
D
D
C
C
B
D
C
D
B
6
Лысенко Т.О.
C
B
A
C
C
B
D
C
D
B
7
Голуб А.В.
C
D
A
D
D
D
A
C
C
C
8
Файзулин М.Р.
C
D
A
C
A
B
A
D
C
A
9
Игнатович Р.Т.
C
D
A
C
C
B
D
C
D
D
10
Роднина М.В.
C
D
A
C
C
D
D
A
C
C
11
Правдина М.Л.
C
D
A
C
C
B
D
C
D
B

27. Описание признаков:

VAR5А=«тревога, балл» НОРМА: 0-7
VAR6А=«тревога»
1-норма
2-не норма

28. Подготовка матрицы ответов к статистическому анализу

Номер задания j
Номер
Испытуемого
1
2
3
4
5
6
7
8
9
10
1
1
1
1
1
1
1
0
0
0
0
2
1
1
0
0
0
0
0
0
0
0
3
0
0
0
0
0
0
0
0
0
0
4
0
0
0
0
0
0
0
1
0
0
5
1
1
0
1
1
1
1
1
1
1
6
1
0
1
1
1
1
1
1
1
1
7
1
1
1
0
0
0
0
1
0
0
8
1
1
1
1
0
1
0
0
0
0
9
1
1
1
1
1
1
1
1
1
0
10
1
1
1
1
1
0
1
0
0
0
11
1
1
1
1
1
1
1
1
1
1

29.

30. Что такое переменная?

Переменная (анг. variable) — это то, что можно
измерять или контролировать. Иными словами,
переменная — это то, что изменяется.
ПРИМЕРЫ: анкетные данные, АД, доля зрителей,
скорость, температура, объем, оценка по шкале

31. Характеристики переменных:

Переменные не постоянны, нужно
научиться описывать их изменчивость.
Для этого придуманы описательные
или дескриптивные статистики.

32. Характеристики переменных:

Медиана (Ме) разбивает выборку на две
равные части. Половина значений переменной
лежит ниже медианы, половина — выше.
Ме дает общее представление о том, где
сосредоточены значения переменной, иными
словами, где находится ее центр.

33.

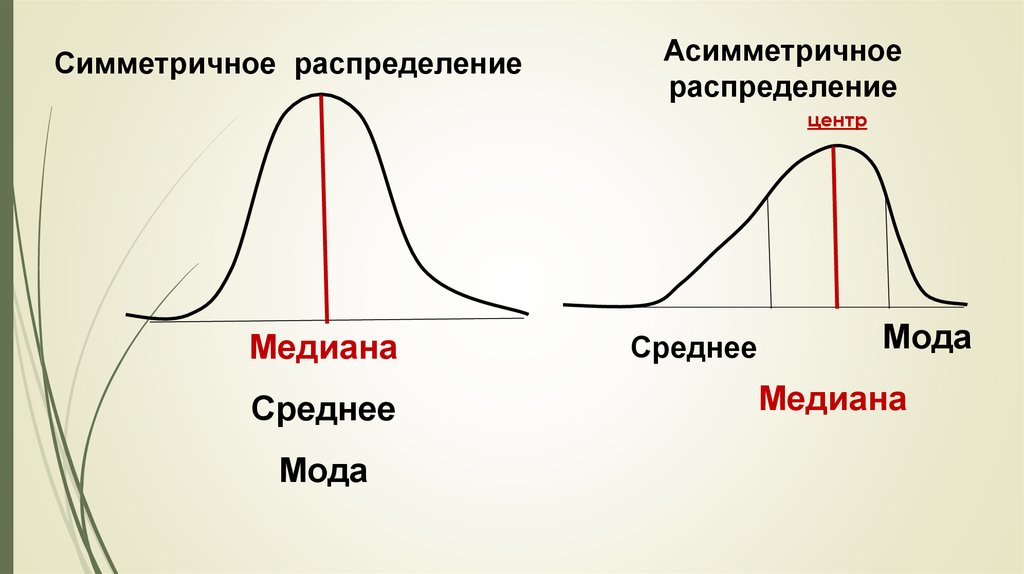
Симметричное распределение
Асимметричное
распределение
центр
Медиана
Среднее
Мода
Среднее
Мода
Медиана

34.

35. Характеристики переменных:

Мода (Мо) представляет собой
максимально часто встречающееся
значение переменной (иными словами,
наиболее
«модное»
значение
переменной).

36.

Симметричное распределение
Асимметричное
распределение
частота
Мода
Медиана
Среднее
Среднее
Мода
Медиана

37. Характеристики переменных:

Среднее - сумма значений
переменной, деленная на n (число
значений переменной).

38.

Симметричное распределение
Среднее
Медиана
Мода
Асимметричное
распределение
Среднее
Мода
Медиана

39.

Характеристики переменных:
Минимум и максимум — это минимальное и
максимальное значения переменной.
Минимум
Максимум

40. Характеристики переменных:

Дисперсия
данной переменной.
мера
разброса

41. Характеристики переменных:

квартили,
коэффициент асимметрии,
эксцесс,
коэффициент корреляции и др.

42. Характеристики переменных:

квартили,
Квартили
коэффициент асимметрии,
эксцесс,
коэффициент корреляции и др.

43.

Эксцесс – это показатель относительной крутости
кривой вариационного ряда по сравнению с
нормальным
распределением.
Эксцесс
нормально распределенной случайной величины
равен 0.

44.

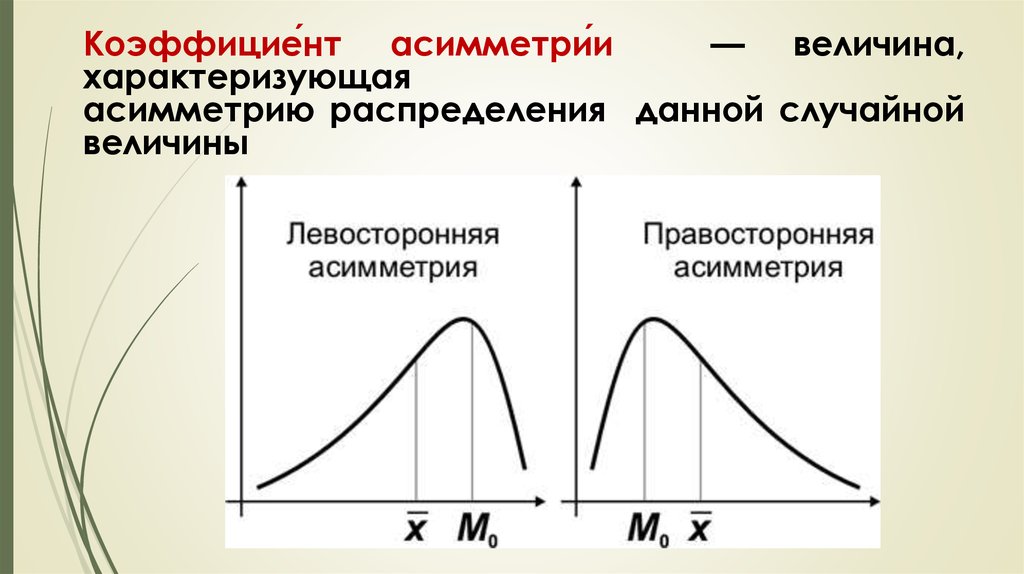
Коэффицие́нт асимметри́и
— величина,
характеризующая
асимметрию распределения данной случайной
величины

45.

46. Понятие «Нулевая гипотеза»:

«Нулевая гипотеза» — это
предположение о том, что в
сравниваемых группах отсутствует
различие в распределении частот.

47. Уровень значимости

- это
такая вероятность, которую
принимают за основу при
статистической оценке гипотезы.

48. Уровень значимости 5%.

В качестве максимального уровня значимости,
при котором нулевая гипотеза еще
отклоняется, принимается 5%.
При уровне значимости более 5% «нулевая
гипотеза» принимается, различия между
сравниваемыми совокупностями принимаются
статистически незначимыми.

49. Как выбрать статистический метод?

50. Как выбрать статистический метод?

Если признак числовой, стоит подумать,
нормально ли его распределение.
Если Вы имеете дело с порядковыми и
качественными признаками, то подходят
только непараметрические методы.
Если данных мало (или Вы не хотите
думать
о
типе
распределения)
воспользуйтесь
непараметрическими
методами.

51. Основные цели первичного (разведочного) анализа

Определение характера
распределений
переменных, визуальный
анализ зависимостей и
идентификация возможных
выбросов.
Нормальное
Можно применять
стандартные методы:
t-критерии и
дисперсионный анализ.
Отличное от нормального
(или малая выборка)
Необходимо использовать
непараметрические критерии.

52. Проверка на нормальность:

Визуальный метод
График вероятности
Критерий Колмогорова-Смирнова (K-S).
Если K-S d>0,0895, распределение не
соответствует нормальному на уровне
значимости 0,05.
Критерий Шапиро-Уилка
Совпадение значений моды и медианы
Равенство нулю показателей асимметрии и
эксцесса (таблицы критических значений
для заданной выборки)

53. Нормальное распределение - фундаментальный закон природы Мировая практика: 20-25% !!!

Histogram: Мочевина,норма
K-S d=,08817, p> .20; Lilliefors p> .20
Expected Normal
10
9
8
No. of obs.
7
6
5
4
3
2
1
0
1
2
3
4
5
6
X <= Category Boundary
7
8
9
10

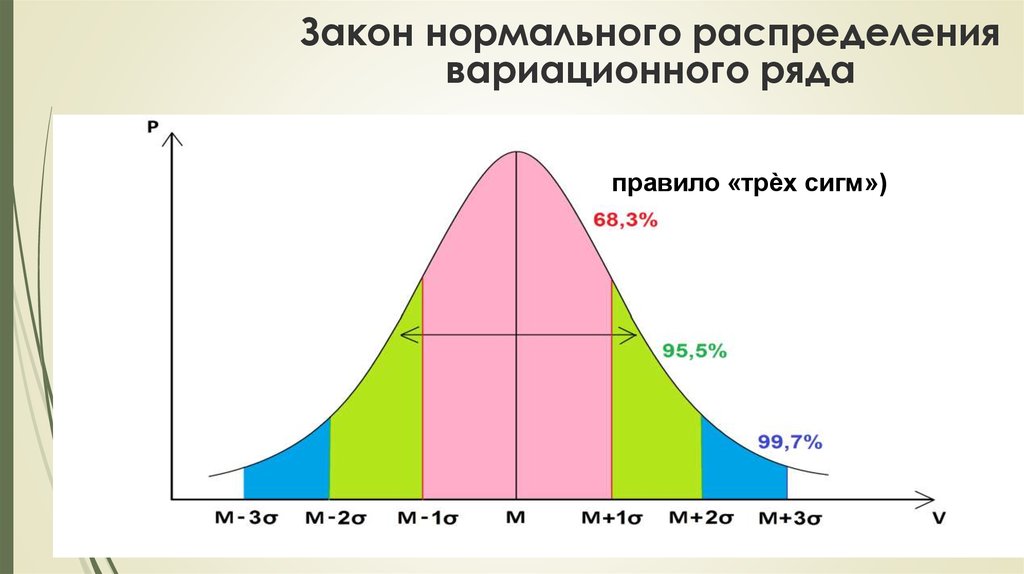
54. Закон нормального распределения вариационного ряда

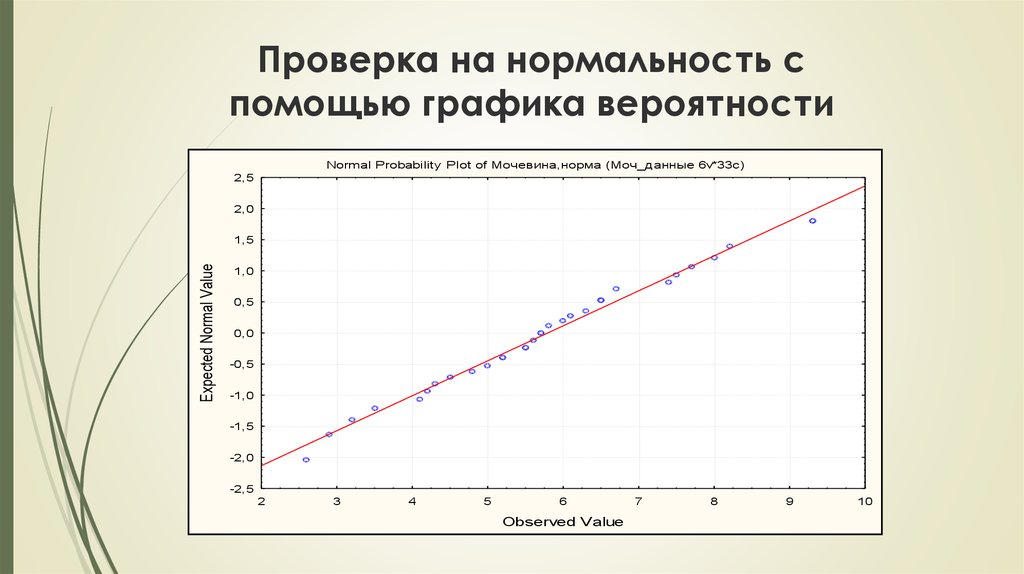
(правило «трѐх сигм»)

55. Проверка на нормальность с помощью графика вероятности

Normal Probability Plot of Мочевина,норма (Моч_данные 6v*33c)
2,5
2,0
Expected Normal Value
1,5
1,0
0,5
0,0
-0,5
-1,0
-1,5
-2,0
-2,5
2
3
4
5
6
Observed Value
7
8
9
10

56. Распределения отличное от нормального

Histogram: Белок_норма
K-S d=,12365, p> .20; Lilliefors p> .20
Expected Normal
11
10
9
8
No. of obs.
7
6
5
4
3
2
1
0
50
55
60
65
70
X <= Category Boundary
75
80
85

57. Распределения отличное от нормального

Histogram: Белок_дин(7)
K-S d=,12782, p> .20; Lilliefors p> .20
Expected Normal
8
7
6
No. of obs.
5
4
3
2
1
0
55
60
65
70
75
X <= Category Boundary
80
85
90

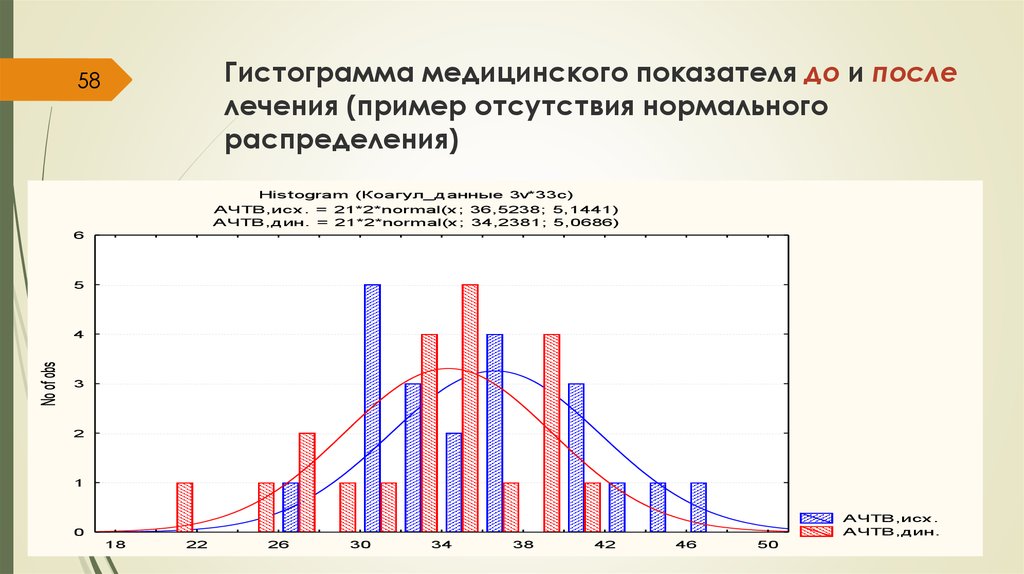
58. Гистограмма медицинского показателя до и после лечения (пример отсутствия нормального распределения)

58
Histogram (Коагул_данные 3v*33c)
АЧТВ,исх. = 21*2*normal(x; 36,5238; 5,1441)
АЧТВ,дин. = 21*2*normal(x; 34,2381; 5,0686)
6
5
No of obs
4
3
2
1
АЧТВ,исх.
АЧТВ,дин.
0
18
22
26
30
34
38
42
46
50

59.

Нормальное (гауссово, симметричное,
колоколообразное) распределение – используем
параметрические методы
Р
Х

60.

В противном случае должны
применяться
непараметрические методы.
60

61. Непараметрические методы

- это
методы
статистической
обработки
данных,
применение
которых не требует знания закона
распределения изучаемых признаков в
совокупности
и
вычисления
их
основных параметров.

62.

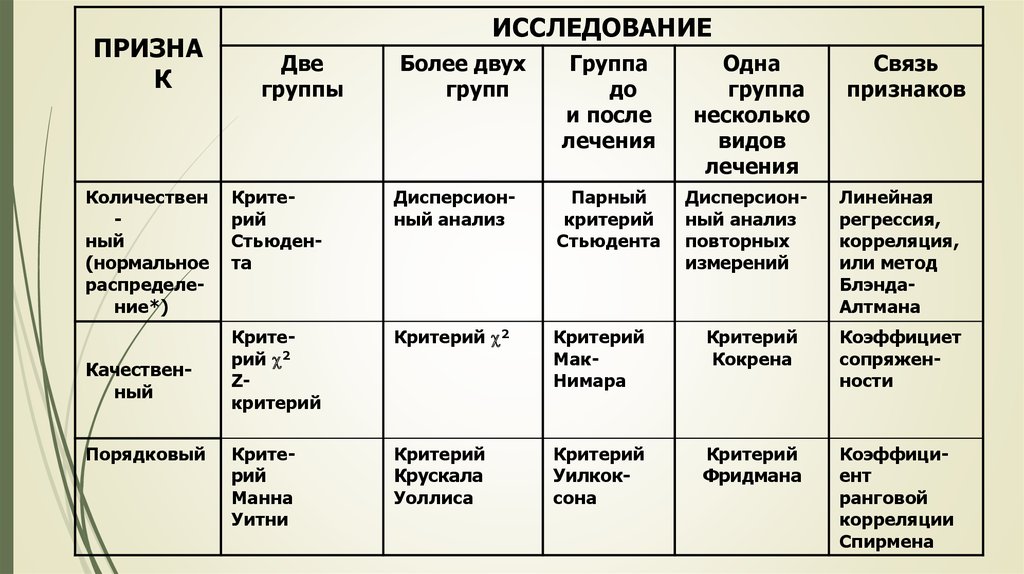
ПРИЗНА
К
Количествен
ный
(нормальное
распределение*)
Качественный
Порядковый
ИССЛЕДОВАНИЕ
Две
группы
Более двух
групп
Группа
до
и после
лечения
Одна
группа
несколько
видов
лечения
Дисперсионный анализ
повторных
измерений
Связь
признаков
Критерий
Стьюдента
Дисперсионный анализ
Парный
критерий
Стьюдента
Линейная
регрессия,
корреляция,
или метод
БлэндаАлтмана
Критерий 2
Zкритерий
Критерий 2
Критерий
МакНимара
Критерий
Кокрена
Коэффициет
сопряженности
Критерий
Манна
Уитни
Критерий
Крускала
Уоллиса
Критерий
Уилкоксона
Критерий
Фридмана
Коэффициент
ранговой
корреляции
Спирмена

63. Принцип действия критериев:

Сравниваются нужные признаки или группы.
Проверяется нулевая гипотеза. Находится
фактическая вероятность ошибки отклонить
верную нулевую гипотезу (р).
Говоря упрощенно, р это вероятность
справедливости нулевой гипотезы.

64. Принцип действия критериев:

Максимальную приемлемую вероятность
отвергнуть нулевую гипотезу называют
уровнем значимости и обозначают .
Обычно в медико-биологических
исследованиях принимают = 0.05.
Если р < 0,05 нулевая гипотеза отвергается,
следовательно найдено статистически
значимое различие в сравниваемых группах.

65.

Сравнение различных совокупностей
«Нулевая гипотеза»
Предположение о том, что в сравниваемых группах отсутствуют
различия в распределении частот
расчет «ожидаемых» величин (результатов)
сравнение «ожидаемых» величин и фактических
разницы нет
разница есть
Статистической значимости различий нет
Статистическая значимость различий есть
р >0,05
р <0,05

66. Корреляция и причинная связь

Когда проверка гипотезы показывает, что
существует значимая линейная связь между
переменными, исследователь должен
рассмотреть возможные виды связи между
переменными и выбрать ту, которая диктуется
логикой исследования.

67. Пример разброса значений двух величин

разброс значений
значения 4 столбца
60
50
40
30
коэффициент
корреляции равен 0,15
20
10
0
-10
-10 0
10
20
значения 3 столбца
30
40

68. Пять видов связи между переменными

1. Прямая причинно-следственная связь
2. Обратная причинно-следственная связь
3. Связь вызвана третьей (скрытой)
переменной
4. Взаимосвязь вызвана несколькими
скрытыми переменными
5. Связи нет, наблюдаемая зависимость
случайна

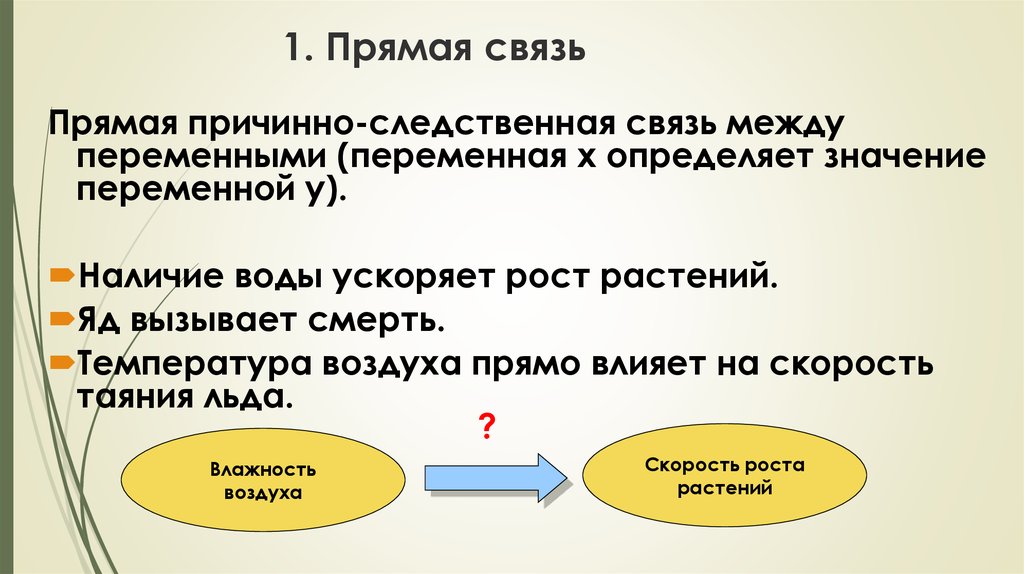
69. 1. Прямая связь

Прямая причинно-следственная связь между
переменными (переменная х определяет значение
переменной у).
Наличие воды ускоряет рост растений.
Яд вызывает смерть.
Температура воздуха прямо влияет на скорость
таяния льда.
?
Влажность
воздуха
Скорость роста
растений

70. 2. Обратная связь

Обратная причинно-следственная связь между
переменными (переменная у определяет значение
переменной х).
Исследователь может думать, что чрезмерное
потребление кофе вызывает нервозность. Но,
может быть, очень нервный человек выпивает кофе,
чтобы успокоить свои нервы?
Чрезмерное
потребление
кофе
?
Нервозность

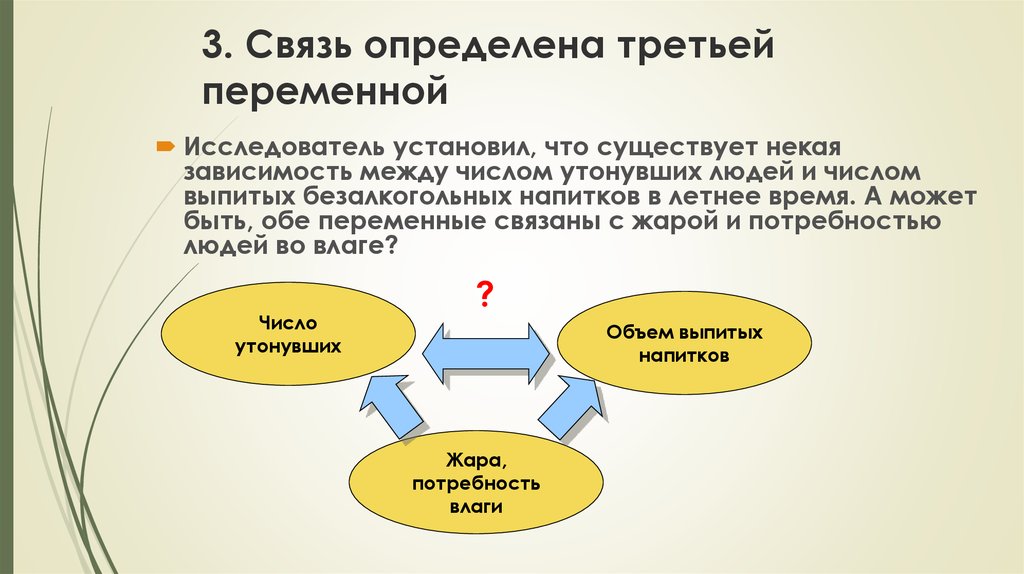
71. 3. Связь определена третьей переменной

Исследователь установил, что существует некая
зависимость между числом утонувших людей и числом
выпитых безалкогольных напитков в летнее время. А может
быть, обе переменные связаны с жарой и потребностью
людей во влаге?
Число
утонувших
?
Объем выпитых
напитков
Жара,
потребность
влаги

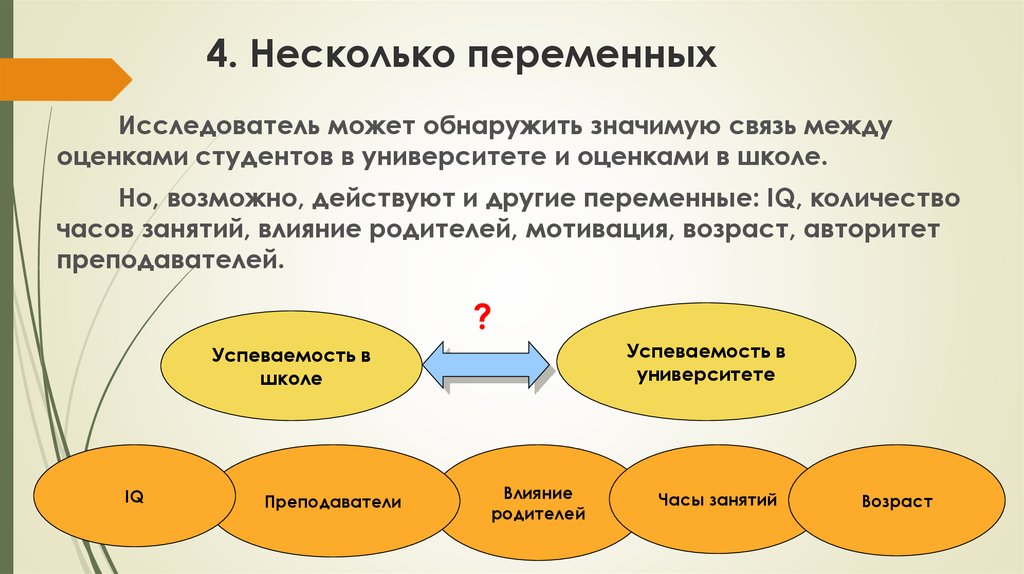
72. 4. Несколько переменных

Исследователь может обнаружить значимую связь между
оценками студентов в университете и оценками в школе.
Но, возможно, действуют и другие переменные: IQ, количество
часов занятий, влияние родителей, мотивация, возраст, авторитет
преподавателей.
?
Успеваемость в
университете
Успеваемость в
школе
IQ
Преподаватели
Влияние
родителей
Часы занятий
Возраст

73. 5. Зависимость случайна

Исследователь может найти значимую зависимость между
увеличением количества людей, которые занимаются спортом и
увеличением количества людей, которые совершают преступления.
Но здравый смысл говорит, что любая связь между этими двумя
переменными должна быть случайной.
Число людей,
регулярно
занимающихся
спортом
?
Число
преступлений

74. Диаграммы

Диаграмма – графическое изображение
статистических величин с помощью различных
геометрических фигур, знаков
I. Классификация диаграмм по форме:
ОБЪЕМНЫЕ
ПЛОСКОСТНЫЕ
ЛИНЕЙНЫЕ
90
90
80
80
70
70
60
60
50
50
40
40
30
30
20
20
10
10
120
90
60
30
0
1 кв
2 кв
3 кв
0
1 кв
2 кв
3 кв
0
1 кв
2 кв
3 кв
7
4

75.

76.

II. Классификация диаграмм по
назначению:
2. Диаграммы структуры
ВНУТРИ-ЛЕНТОЧНЫЕ
Намибия
ОАЭ
СЕКТОРНЫЕ
Прочие
14%
Травмы
15%
ССС
55%
Онко
16%
7
6

77.

78.

79.

80.

81.

82.

83.

84.

85.

II. Классификация диаграмм по назначению:
3. Диаграммы динамики
РАДИАЛЬНАЯ
ЛИНЕЙНЫЕ
янв
дек
3780
3775
ноя
100
фев
март
50
3770
окт
3765
апр
0
3760
сен
3755
май
авг
3750
2005
2006
2007
2008
2009
2010
июнь
июль
8
5

86. Финансирование медицинской помощи по Программе государственных гарантий в 1999-2005 гг. (млн.руб.)

12450,4
5696
8335,0
6222,9
4022,7
4524
6875,1
5360,7
5851,7
4897,2
4794,3
3344,4
6754,4
3027,9
1999
1704,9
1875
2000
2001
2494,6
2483,3
2002
2003
2004
ОМС
5198,9
994,8
Бюджет
10559,9
2005

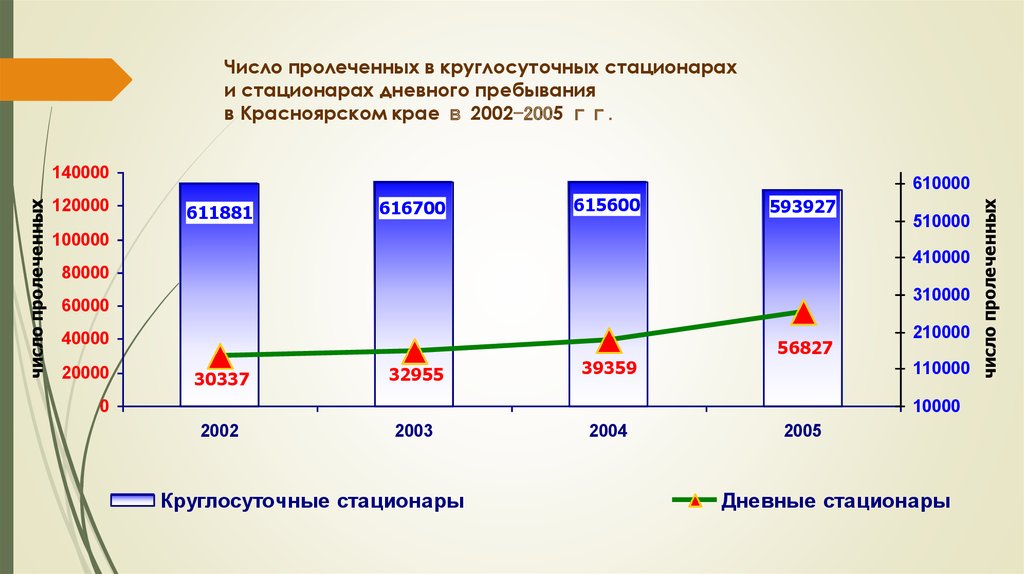
87. Число пролеченных в круглосуточных стационарах и стационарах дневного пребывания в Красноярском крае в 2002-2005 гг.

120000
610000
611881
616700
615600
593927
510000
100000
410000
80000
310000
60000
40000
20000
30337
32955
39359
56827
210000
110000
0
10000
2002
2003
Круглосуточные стационары
2004
2005
Дневные стационары
число пролеченных
число пролеченных
140000

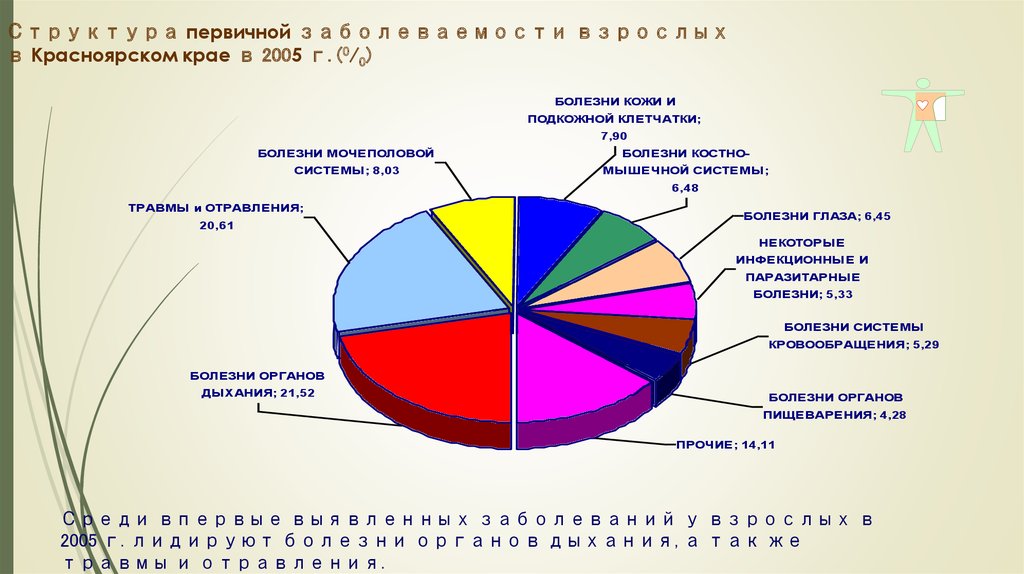
88. Структура первичной заболеваемости взрослых в Красноярском крае в 2005 г. (0/0)

БОЛЕЗНИ КОЖИ И
ПОДКОЖНОЙ КЛЕТЧАТКИ;
7,90
БОЛЕЗНИ МОЧЕПОЛОВОЙ
БОЛЕЗНИ КОСТНО-
СИСТЕМЫ; 8,03
МЫШЕЧНОЙ СИСТЕМЫ;
6,48
ТРАВМЫ и ОТРАВЛЕНИЯ;
20,61
БОЛЕЗНИ ГЛАЗА; 6,45
НЕКОТОРЫЕ
ИНФЕКЦИОННЫЕ И
ПАРАЗИТАРНЫЕ
БОЛЕЗНИ; 5,33
БОЛЕЗНИ СИСТЕМЫ
КРОВООБРАЩЕНИЯ; 5,29
БОЛЕЗНИ ОРГАНОВ
ДЫХАНИЯ; 21,52
БОЛЕЗНИ ОРГАНОВ
ПИЩЕВАРЕНИЯ; 4,28
ПРОЧИЕ; 14,11
Среди впервые выявленных заболеваний у взрослых в
2005 г. лидируют болезни органов дыхания, а так же
травмы и отравления.

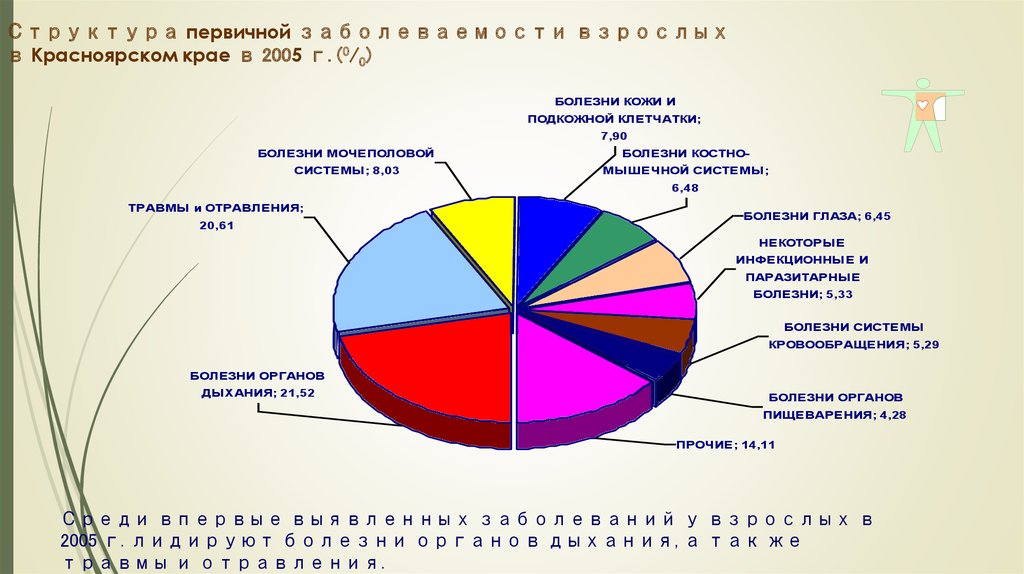
89. Структура первичной заболеваемости взрослых в Красноярском крае в 2005 г. (0/0)

БОЛЕЗНИ КОЖИ И
ПОДКОЖНОЙ КЛЕТЧАТКИ;
7,90
БОЛЕЗНИ МОЧЕПОЛОВОЙ
БОЛЕЗНИ КОСТНО-
СИСТЕМЫ; 8,03
МЫШЕЧНОЙ СИСТЕМЫ;
6,48
ТРАВМЫ и ОТРАВЛЕНИЯ;
20,61
БОЛЕЗНИ ГЛАЗА; 6,45
НЕКОТОРЫЕ
ИНФЕКЦИОННЫЕ И
ПАРАЗИТАРНЫЕ
БОЛЕЗНИ; 5,33
БОЛЕЗНИ СИСТЕМЫ
КРОВООБРАЩЕНИЯ; 5,29
БОЛЕЗНИ ОРГАНОВ
ДЫХАНИЯ; 21,52
БОЛЕЗНИ ОРГАНОВ
ПИЩЕВАРЕНИЯ; 4,28
ПРОЧИЕ; 14,11
Среди впервые выявленных заболеваний у взрослых в
2005 г. лидируют болезни органов дыхания, а так же
травмы и отравления.

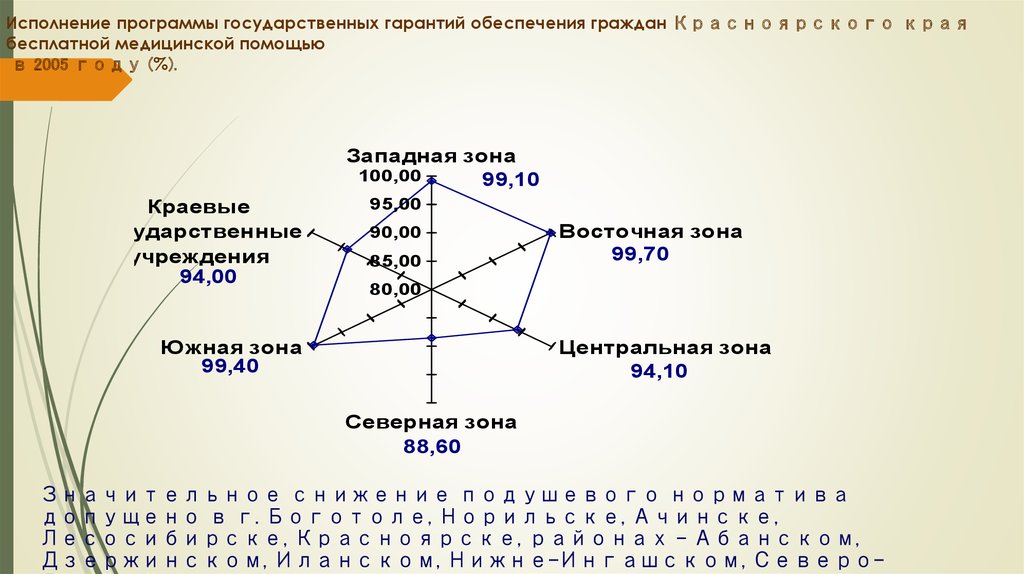
90. Исполнение программы государственных гарантий обеспечения граждан Красноярского края бесплатной медицинской помощью в 2005 году

(%).
Западная зона
100,00
99,10
Краевые
государственные
учреждения
94,00
95,00
90,00
85,00
Восточная зона
99,70
80,00
Южная зона
99,40
Центральная зона
94,10
Северная зона
88,60
Значительное снижение подушевого норматива
допущено в г. Боготоле, Норильске, Ачинске,
Лесосибирске, Красноярске, районах – Абанском,
Дзержинском, Иланском, Нижне-Ингашском, Северо-

91. Кумулятивное число зарегистрированных случаев ВИЧ-инфекции в Красноярском крае в 1989-2005 г.г.

Кумулятивное число зарегистрированных случаев ВИЧинфекции в Красноярском крае в 1989-2005 г.г.
1989-1999
2000
2001
2002
2003
2004
2005
6233
5115
5595
4434
3319
994
215
По уровню пораженности Красноярский край относится к
субъектам Российской Федерации с высоким уровнем
развития эпидемии (от 151 до 300 ВИЧ-инфицированных на 100 тыс.
населения) и находится на четвертом месте среди
регионов Сибирского федерального округа после

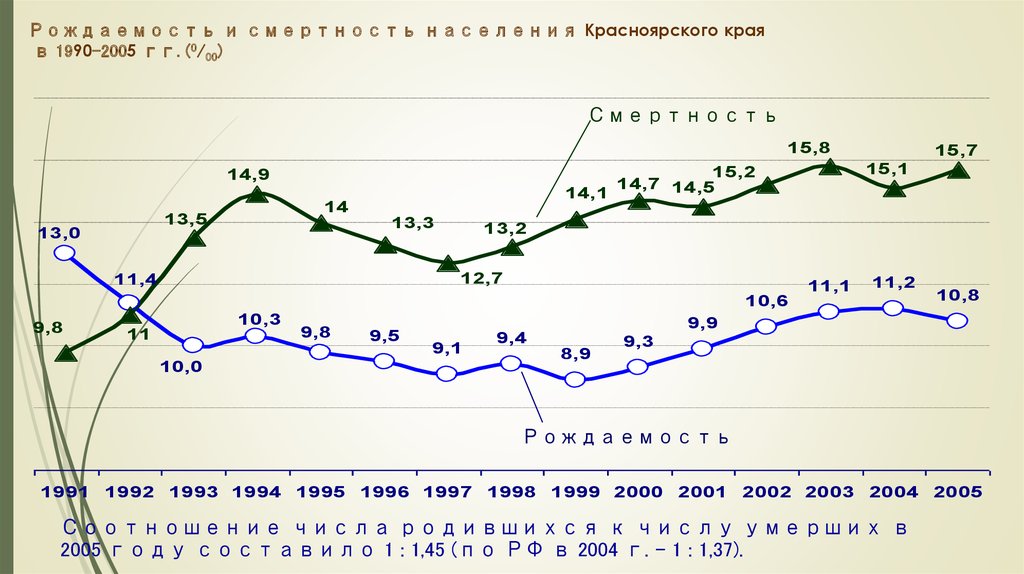
92. Рождаемость и смертность населения Красноярского края в 1990-2005 гг. (0/00)

Смертность
15,8
14
13,5
13,0
15,1
15,2
14,7 14,5
14,1
14,9
13,3
13,2
12,7
11,4
15,7
11,1
11,2
10,6
9,8
10,3
11
10,0
9,8
9,5
10,8
9,9
9,1
9,4
8,9
9,3
Рождаемость
1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005
Соотношение числа родившихся к числу умерших в
2005 году составило 1 : 1,45 (по РФ в 2004 г. – 1 : 1,37).

93. Правила построения диаграмм

1. Должно быть четкое, ясное, краткое
название, порядковый номер
2. Все элементы диаграммы (фигуры,
знаки, окраска, штриховка) должны
быть объяснены на самой диаграмме
или в ее легенде
9
3

94. Правила построения диаграмм

3. Изображаемые графические величины должны
иметь цифровые обозначения на самой
диаграмме или в прилагаемой таблице
4. Данные на диаграмме должны размещаться от
большего к меньшему, слева направо, снизу вверх
и по часовой стрелке,
5. Элемент «прочие» всегда располагается
последним.
9
4

95.

«… Знание статистики подобно
знанию иностранных языков или
алгебры: оно может пригодиться в
любое время и при любых
обстоятельствах»
А.Боули, английский экономист-статистик

96. Благодарю за внимание!