Дерево случайного эксперимента

1.

Дерево случайного
эксперимента.

2.

Пример 1. Двукратное бросание монеты.
Точка S-начальное состояние, когда ни один бросок
ещё не сделан.
При первом броске может выпасть орёл либо решка
(смотрим на рисунке первое бросание).
Изобразим эти два события точками О и Р и проведём к
ним стрелки от точки S вниз влево и вправо.
Стрелки будем называть рёбрами дерева.
Начальная точка S, промежуточные точки (О и Р) и
конечные точки называются вершинами дерева.
Около рёбер напишем вероятности событий: ребро SO
1
1
имеет вероятность и такую же вероятность имеет
2
2
ребро SP.
Важно! При построении дерева нужно следить, чтобы
сумма вероятностей около всех рёбер, выходящих из
одной вершины, была равна единице.
1
1
Проверим: + = 1
2
2

3.

Пример 1. Двукратное бросание монеты.
Предположим сначала, что при первом броске выпал орёл.
При втором броске тоже может выпасть орёл, и тогда
наступит событие «два орла»: ОО. Вероятность выпадения
1
двух орлов равна Р(ОО) = . Но если в первый раз уже
4
1
выпал орёл, то событие ОО наступает с вероятностью –
2
если во второй раз выпадет орёл. То есть условная
вероятность двух орлов при условии, что в первый раз
1
выпал орёл, равна Р(ОО|в 1 – й раз выпал орёл) = .
2
Аналогично для события «первый орел, вторая решка»
1
Р(ОР|в 1 – й раз выпал орёл) = .
2
Рассмотрим правую ветвь нашего дерева.
Для события «первая решка, второй орел» Р(РО|в 1 – й раз
1
выпала решка) = .
2
Для события «первая решка, вторая решка» Р(РР|в 1 – й раз
1
выпала решка) = .
2

4.

Пример 1. Двукратное бросание монеты.
Важно! Около ребер в дереве случайного опыта
подписываются условные вероятности.
Если дерево случайного опыта конечное, то элементарные
события в дереве случайного опыта изображаются цепями,
ведущими из начальной вершины к конечным вершинам
дерева.
Найти вероятность элементарного события
можно с помощью правила умножения
вероятностей: нужно найти произведение
условных вероятностей вдоль соответствующей
цепи.
Например, чтобы найти вероятность события ОР,
нужно умножить вероятности вдоль цепи SOP:
1 1
1
Р(ОР) = ∗ = (на рисунке красная цепочка).
2
2
4

5.

Важно! Чтобы найти вероятность события с помощью дерева, нужно сложить
вероятности всех цепочек, ведущих к этому событию от начальной вершины.

6.

7.

Пример 3 (продолжение)

8.

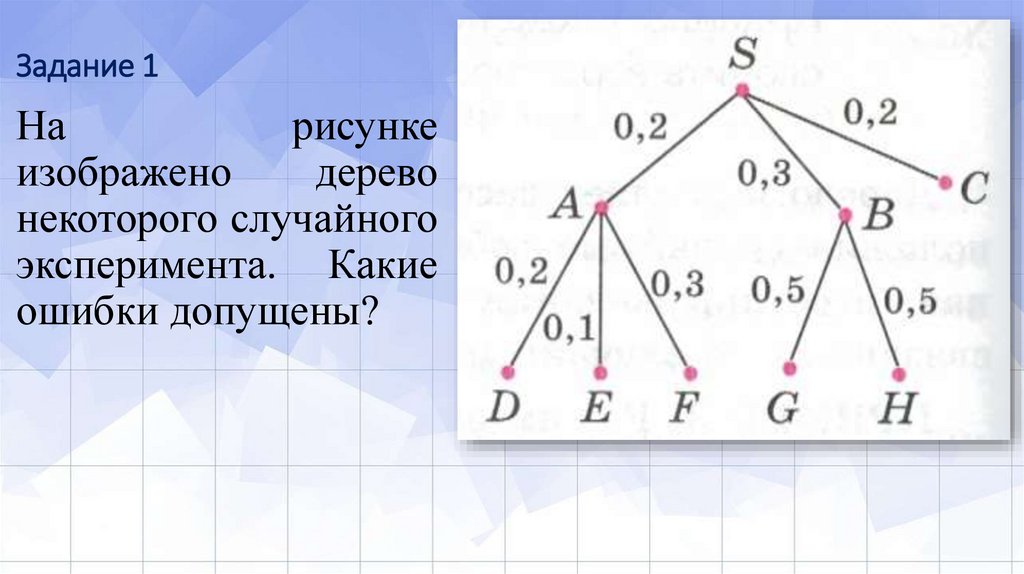
Задание 1
На
рисунке
изображено
дерево
некоторого случайного
эксперимента. Какие
ошибки допущены?

9.

Задание 2
На
рисунке
изображено
дерево
некоторого случайного опыта.
а) Перерисуйте дерево в тетрадь и
подпишите недостающие вероятности
около рёбер.
б) Сколько элементарных событий в этом
эксперименте?
в) Пользуясь правилом умножения
вероятностей, вычислите
вероятности
цепочек SAC и SBE.
г) Найдите вероятность события F.

10.

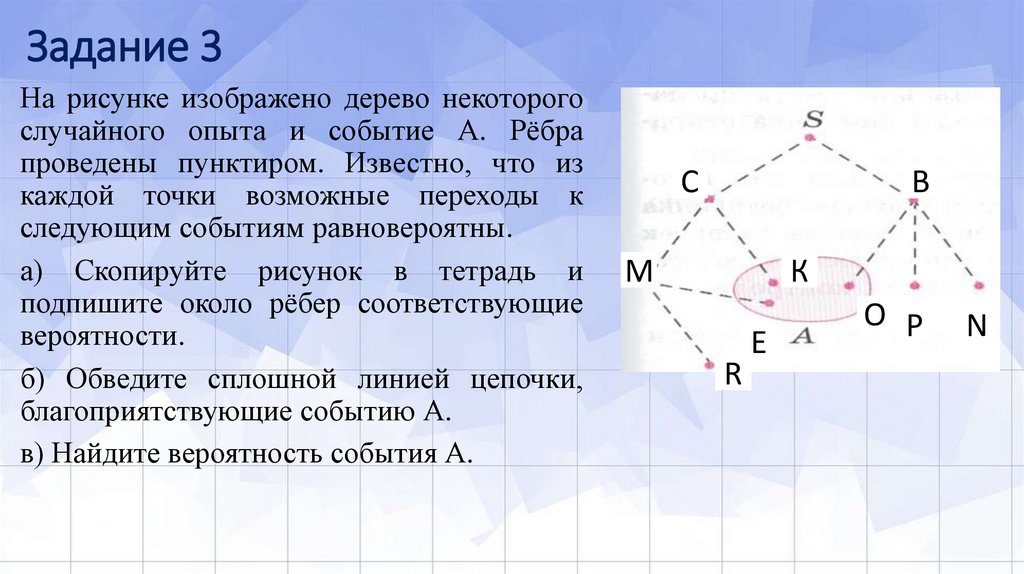
Задание 3
На рисунке изображено дерево некоторого
случайного опыта и событие А. Рёбра
проведены пунктиром. Известно, что из
каждой точки возможные переходы к
следующим событиям равновероятны.
а) Скопируйте рисунок в тетрадь и
подпишите около рёбер соответствующие
вероятности.
б) Обведите сплошной линией цепочки,
благоприятствующие событию А.
в) Найдите вероятность события А.
С
В
М
К
R
E
O P
N

11.

Домашнее задание:
1. На рисунке изображено дерево некоторого случайного
опыта.
а) Изобразите это дерево в своей тетради и подпишите
недостающие вероятности около рёбер.
б) Вычислите вероятности цепочек SAC и SAGF.
2. На рисунке изображено дерево некоторого случайного
опыта и показаны события А и В. Рёбра проведены
пунктиром. Известно, что рёбра, исходящие из одной
вершины, равновероятны.
а) Скопируйте рисунок в тетрадь. Обведите сплошной
линией цепочки, благоприятствующие событию А. Другим
цветом обведите цепочки, благоприятствующие событию В
б) Найдите вероятность события А.
в) Найдите вероятность события В.