Pythagoras’ theorem

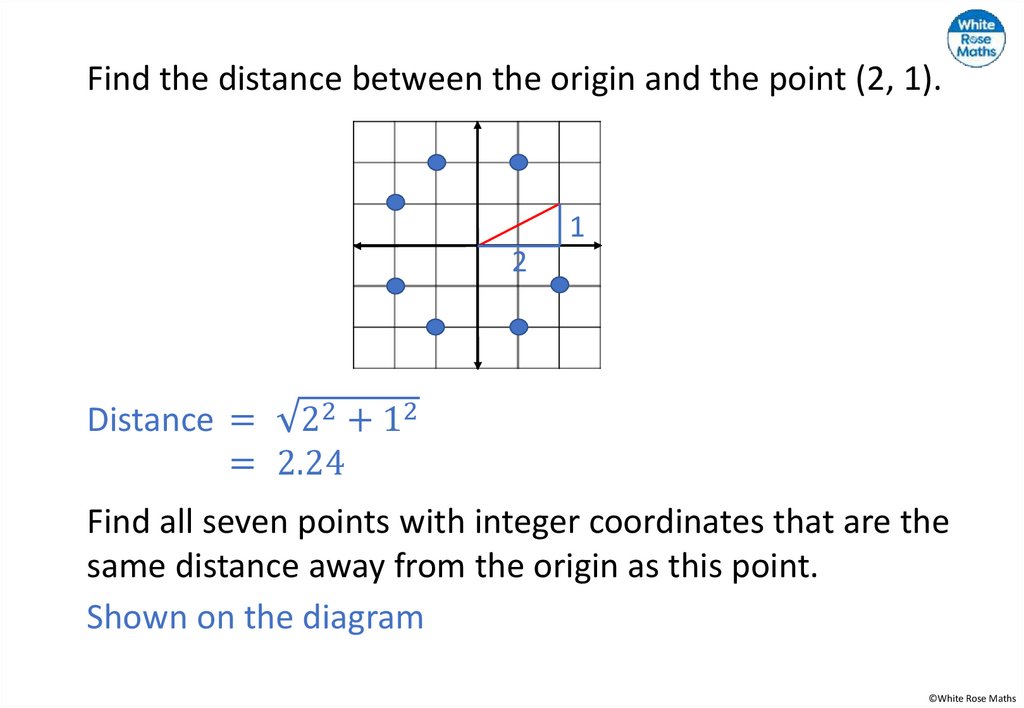
1.

Pythagoras’ Theorem
Year 9
#MathsEveryoneCan

2.

Teddy has 30 counters.
How many different square numbers can he make?
©White Rose Maths

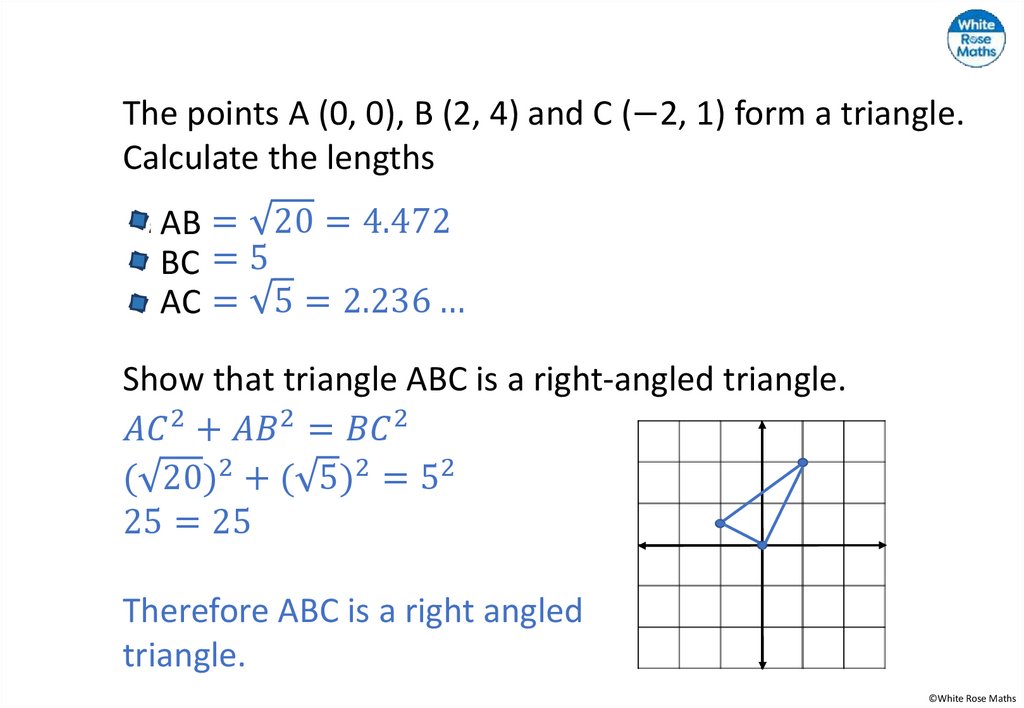
3.

Teddy has 30 counters.
How many different square numbers can he make?
5 different squares
1×1
2×2
3×3
4×4
5×5
©White Rose Maths

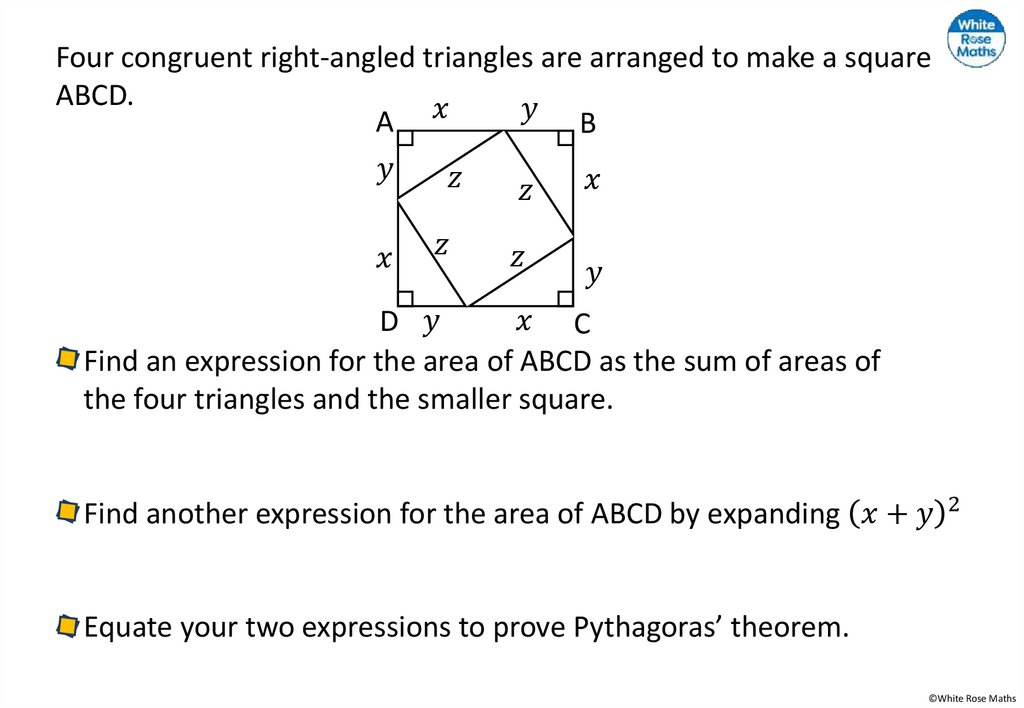
4.

Complete the following using <, > or =
16
22
32
49
64
42
©White Rose Maths

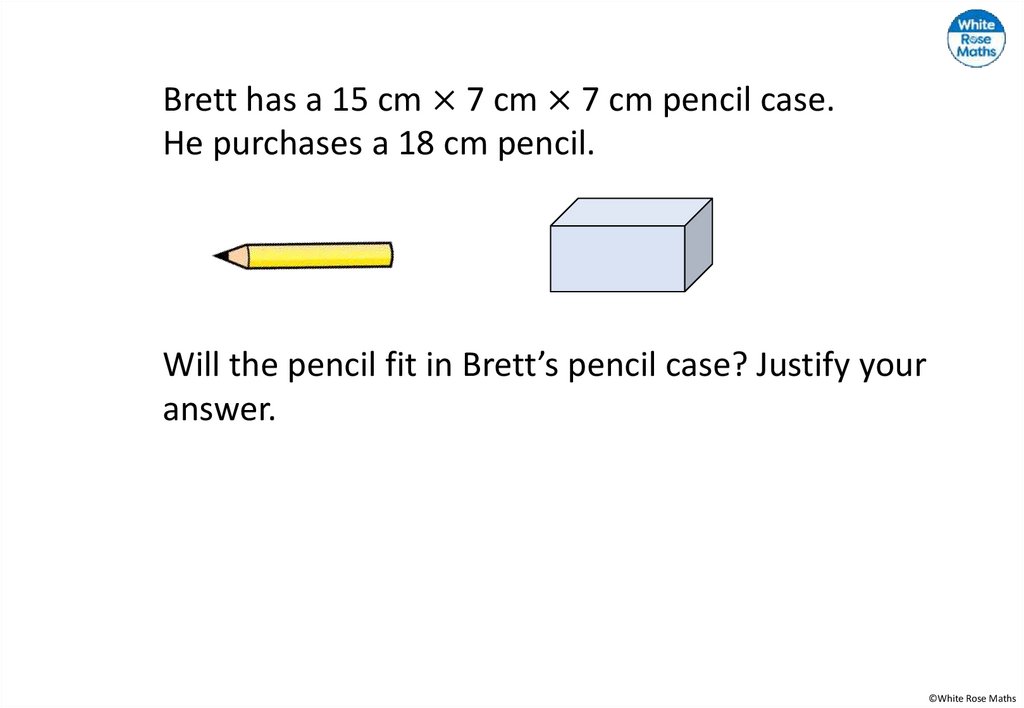
5.

Complete the following using <, > or =
16 =
22
32 >
49
2
<
4
64
©White Rose Maths

6.

Evaluate each card and place them on the number line as
accurately as you can.
121
82
32 + 4
100
0
12 + 92
32 − 12 2
2 × 25
©White Rose Maths

7.

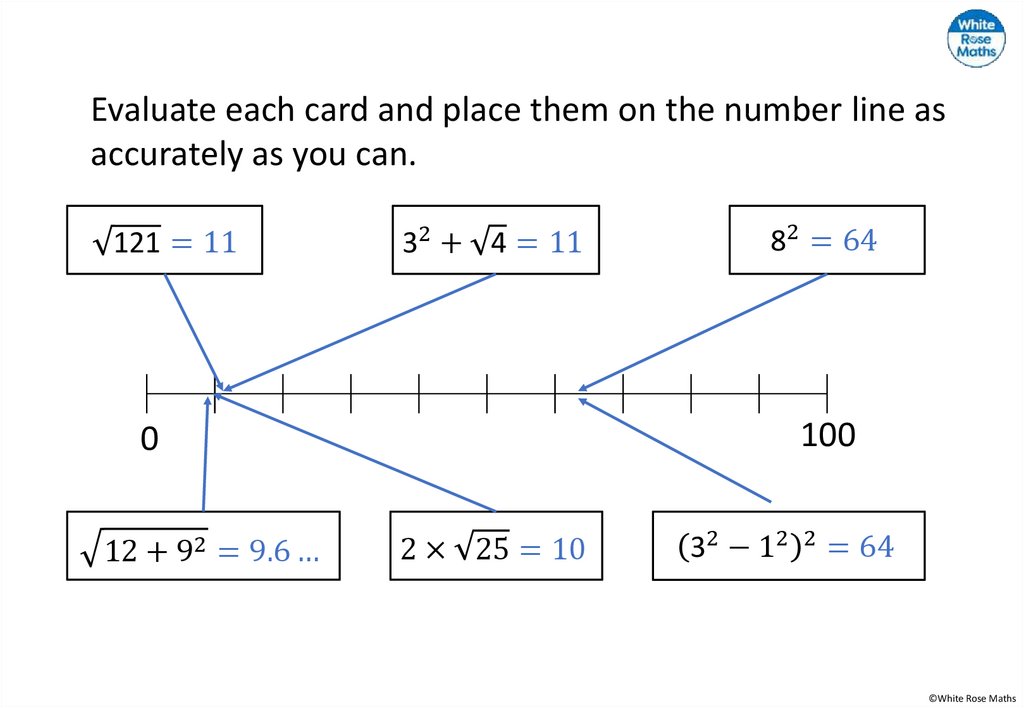
Evaluate each card and place them on the number line as
accurately as you can.
121 = 11
32 + 4 = 11
100
0
12 + 92 = 9.6 …
82 = 64
2 × 25 = 10
32 − 12 2 = 64
©White Rose Maths

8.

“The sum of two different square numbers is
equal to another square number.”
Is this always, sometimes or never true? Justify your answer.
©White Rose Maths

9.

“The sum of two different square numbers is
equal to another square number.”
Is this always, sometimes or never true? Justify your answer.
Sometimes true:
Example: 9 + 16 = 25
Counter example: 9 + 25 = 34
(Square number)
(Not a square number)
Discuss other examples as a class
©White Rose Maths

10.

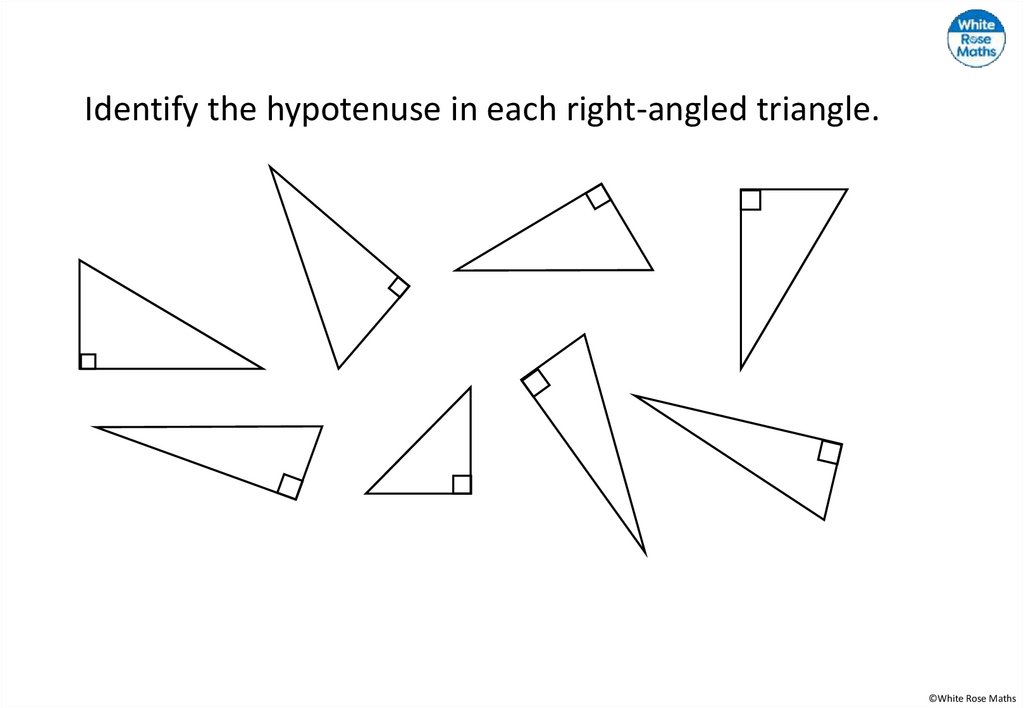
Identify the hypotenuse in each right-angled triangle.
©White Rose Maths

11.

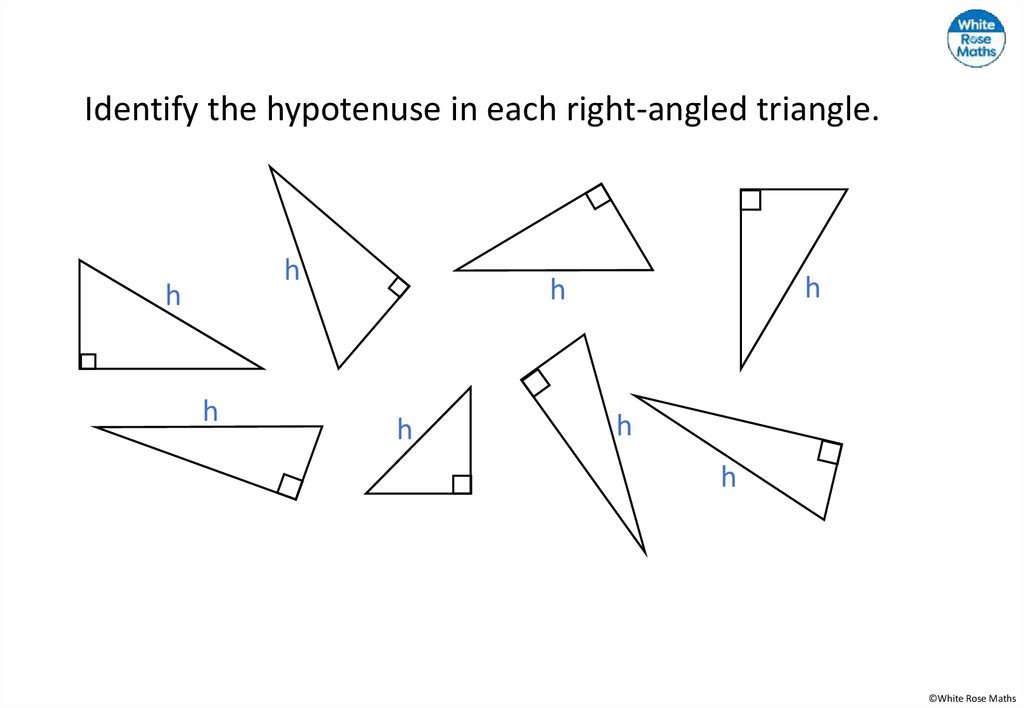
Identify the hypotenuse in each right-angled triangle.
h
h
h
h
h
h
h
h
©White Rose Maths

12.

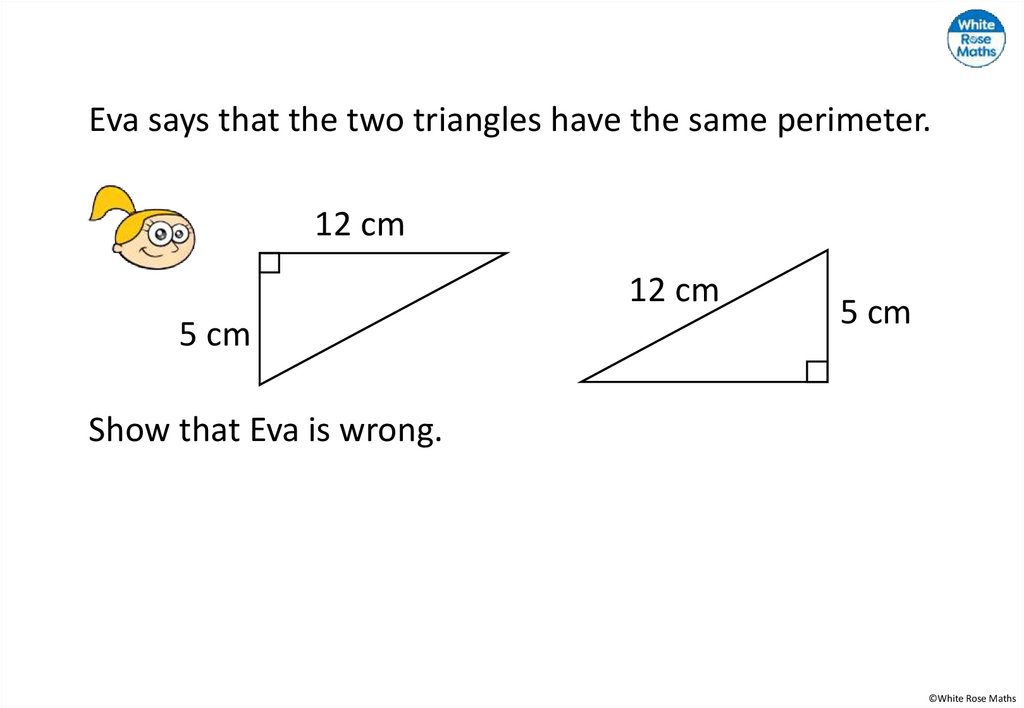
Amir says, “It is not possible to have a hypotenuse in a
square as it is a quadrilateral.”
Do you agree?
©White Rose Maths

13.

Amir says, “It is not possible to have a hypotenuse in a
square as it is a quadrilateral.”
Do you agree?
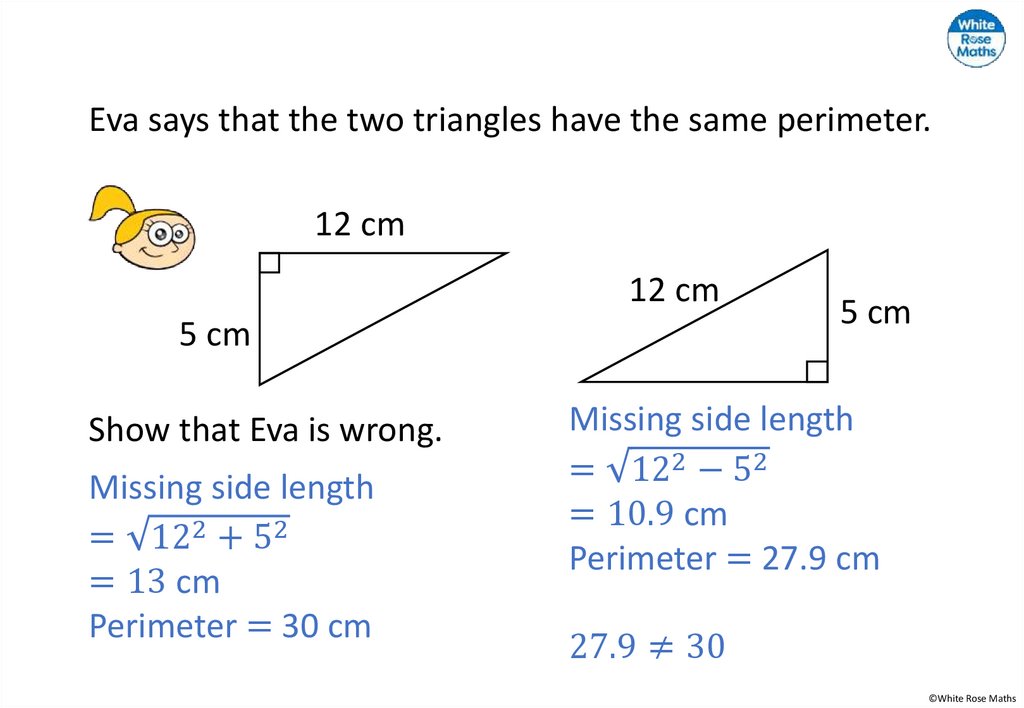
A square does not have a hypotenuse, but drawing the
diagonal of a square divides it into two congruent rightangled triangles. The diagonal is the hypotenuse of both
the triangles formed.
©White Rose Maths

14.

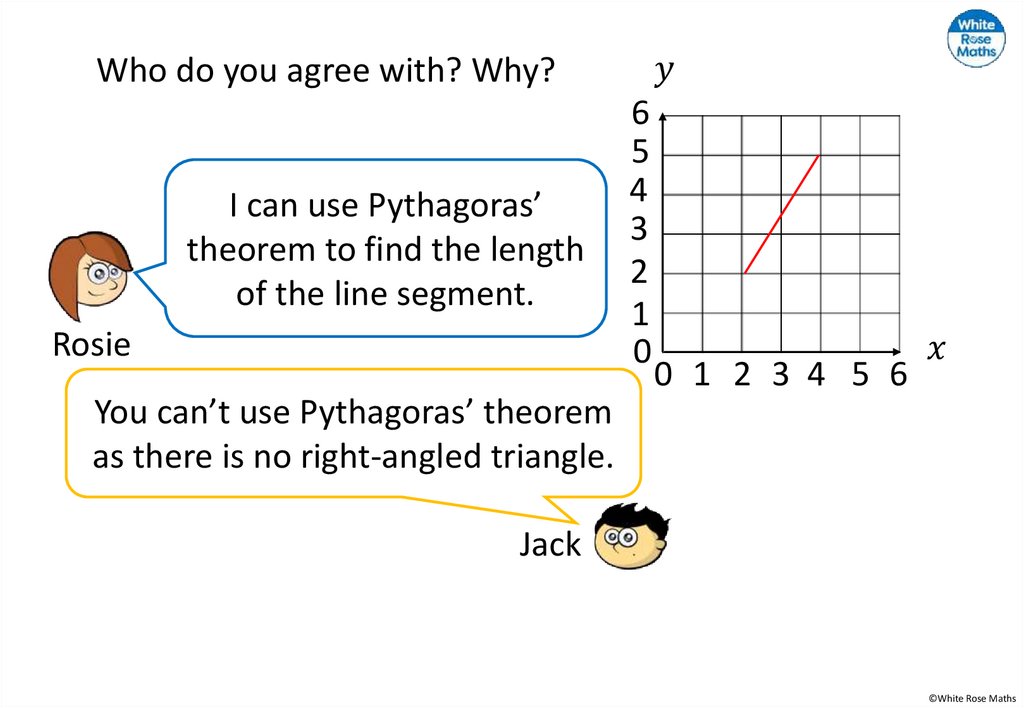
The line shown is the hypotenuse of
a right-angled triangle.
Complete the triangle.
How many possibilities can you find?
©White Rose Maths

15.

The line shown is the hypotenuse of
a right-angled triangle.
Complete the triangle.
How many possibilities can you find?
Possible answers include:
©White Rose Maths

16.

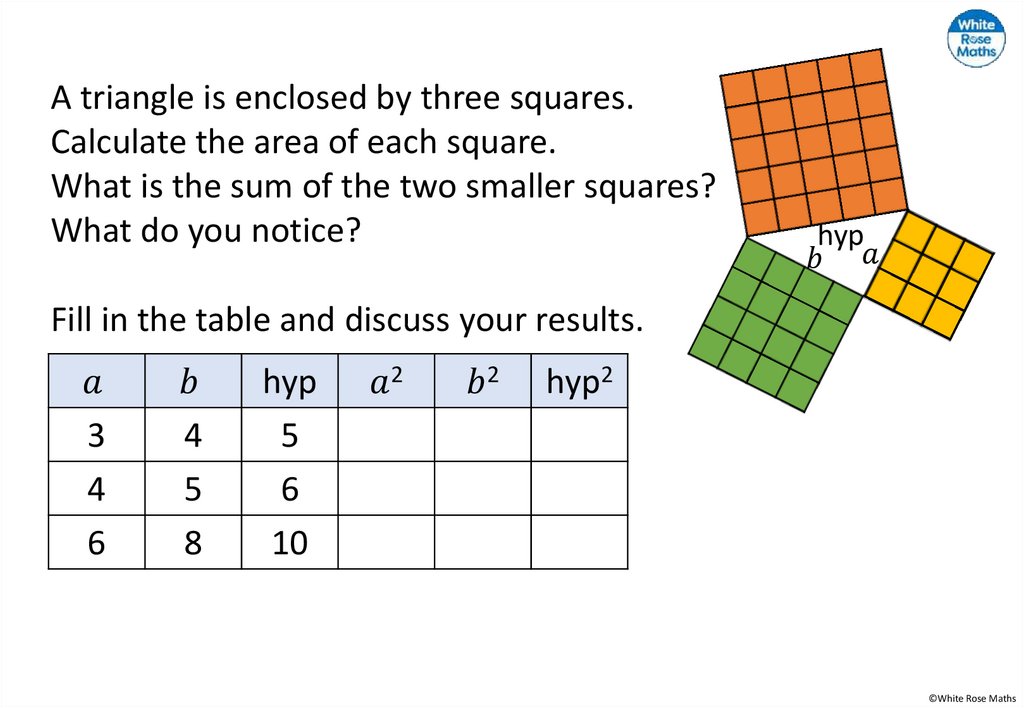
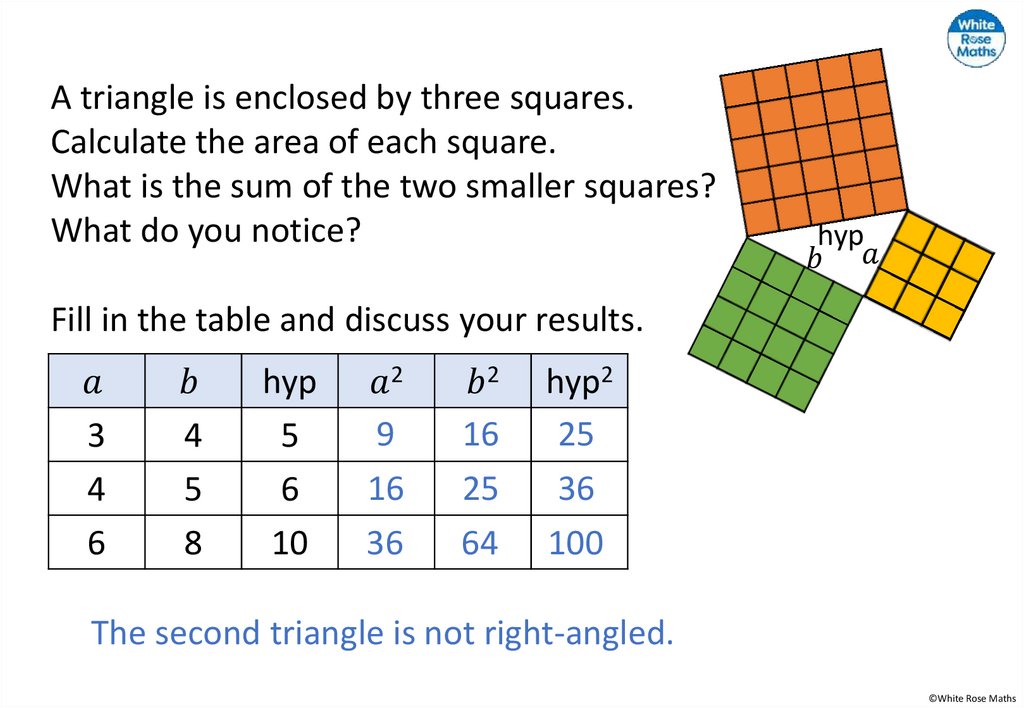
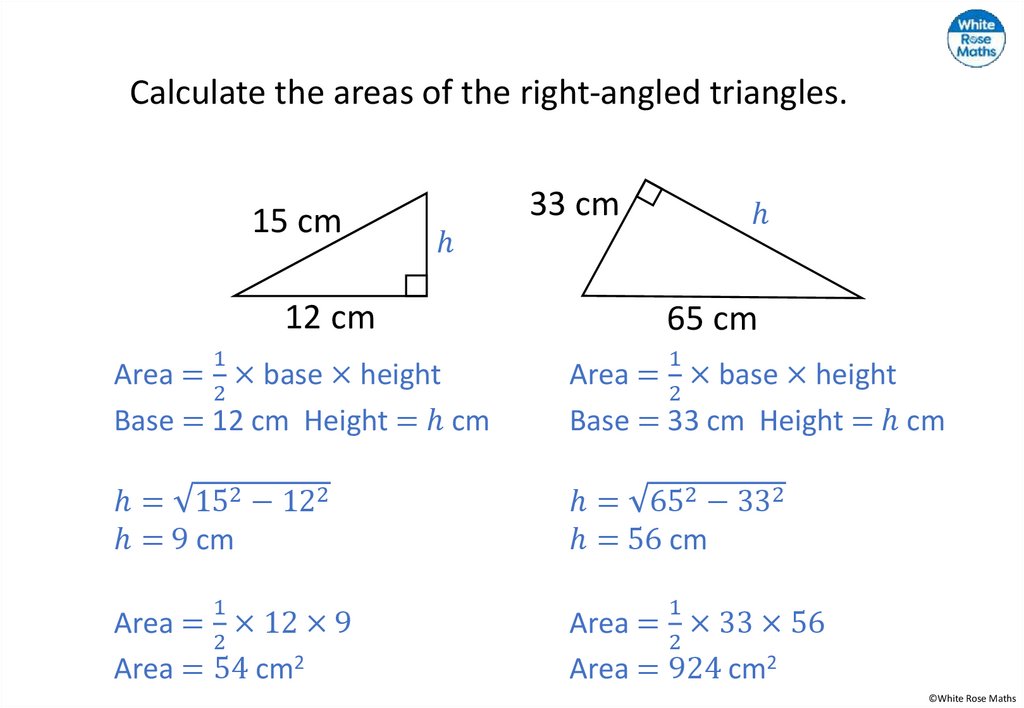
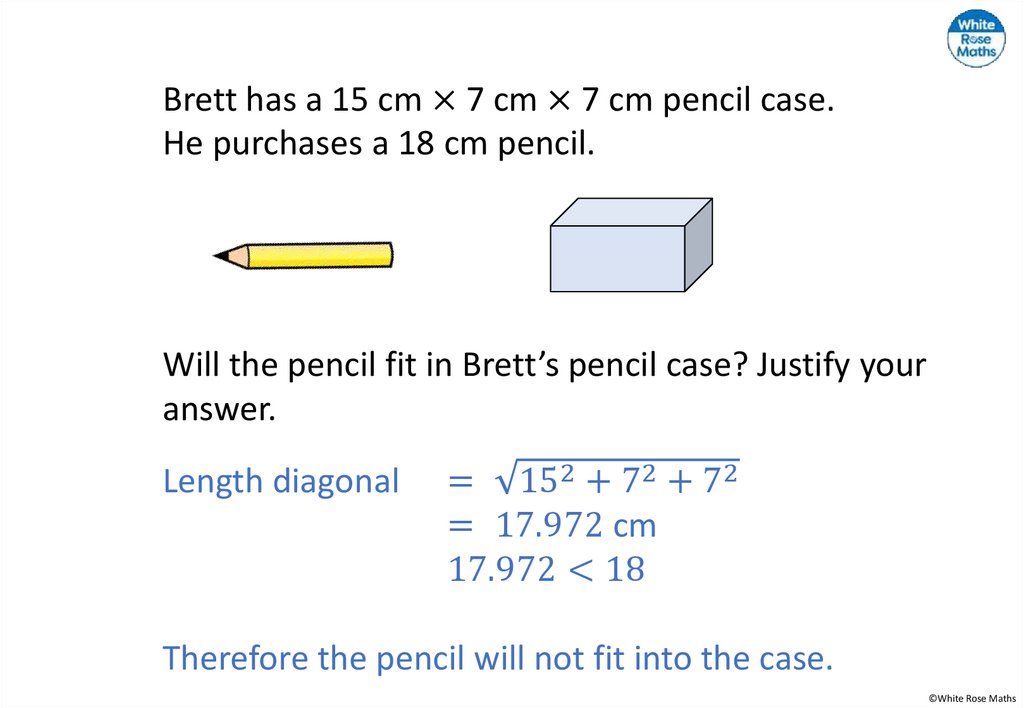
A triangle is enclosed by three squares.
Calculate the area of each square.
What is the sum of the two smaller squares?
What do you notice?
hyp