Вневписанные окружности треугольника: задачи, которые могли бы стать теоремами

1. Вневписанные окружности треугольника: задачи, которые могли бы стать теоремами.

НАУЧНО-ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ «ШАГ в БУДУЩЕЕ»
Вневписанные окружности
треугольника: задачи, которые могли бы
стать теоремами.

2.

ВВЕДЕНИЕ

3.

ВВЕДЕНИЕ
Объект
исследования:
вневписанные
окружности.
Предмет
исследования:
геометрические
задачи на применение определения и свойств
вневписанной окружности, методы и приёмы их
решения.
Методы
исследования:
моделирование,
сравнение,
обобщение,
аналогии,
изучение
литературных и Интернет-ресурсов, анализ и
классификация информации.
Цель
исследования:
Изучить
свойства
вневписанной
окружности,
показать
эффективность применения теории вневписанных
окружностей при решении задач ЕГЭ, составить
сборник некоторых задач, которые могли бы стать
теоремами для учащихся на ЕГЭ.

4.

ВВЕДЕНИЕ
Гипотеза: Скрытая красота и сила вневписанной
окружности как подспорье в решении геометрических
задач ЕГЭ.
При решении задач понадобится геометрическое
воображение и достаточно простые
геометрические
сведения, которые известны всем. При более внимательном
исследовании задач, убеждаешься в их востребованности,
оригинальности, полезности, возникает ощущение красоты,
закона и порядка в природе.
Актуальность
исследования:
Геометрические
конфигурации, связанные с вневписанными окружностями,
очень содержательны и встречаются во многих задачах.
Вневписанная окружность представляется
изысканным элементом геометрии треугольника.

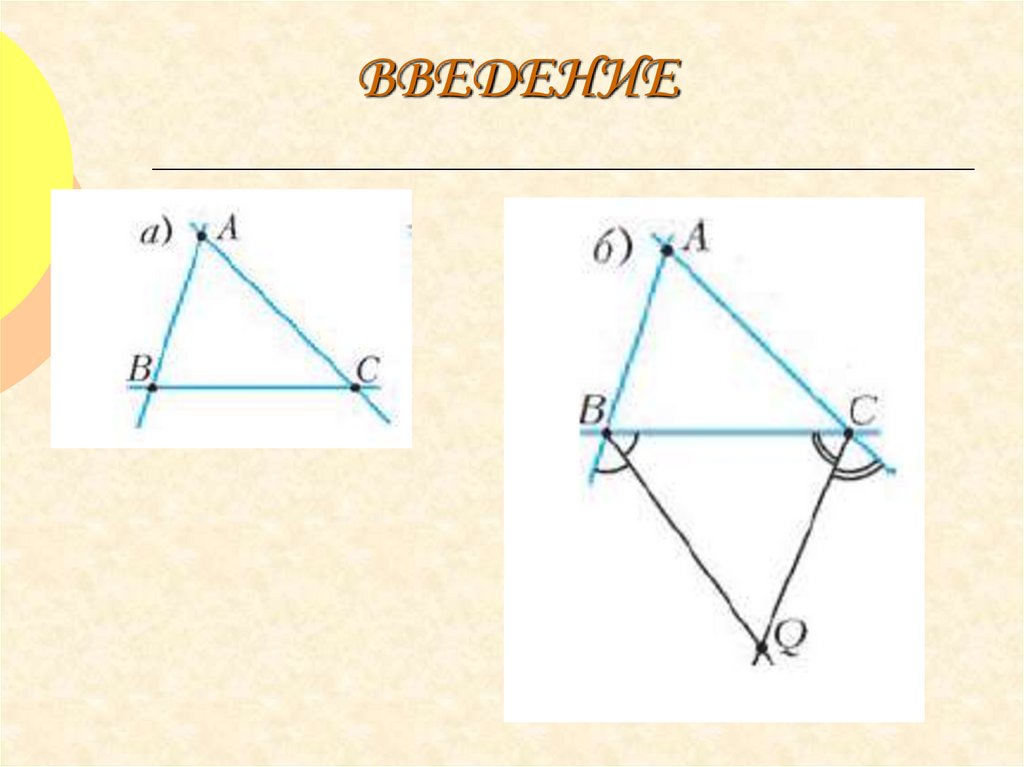
5. Окружность называется вневписанной в треугольник, если она касается одной из сторон треугольника и продолжений двух других

1.1. ПОНЯТИЕ ВНЕВПИСАННОЙ
ОКРУЖНОСТИ ТРЕУГОЛЬНИКА
"Каждый треугольник определяет
семейство окружностей, помогающих
глубже и полнее понять "устройство"
треугольника".
И.Ф. Шарыгин.
В
Окружность называется вневписанной в
треугольник, если она касается одной из
сторон треугольника и продолжений
двух других сторон.
А
N
С
N
К
О

6.

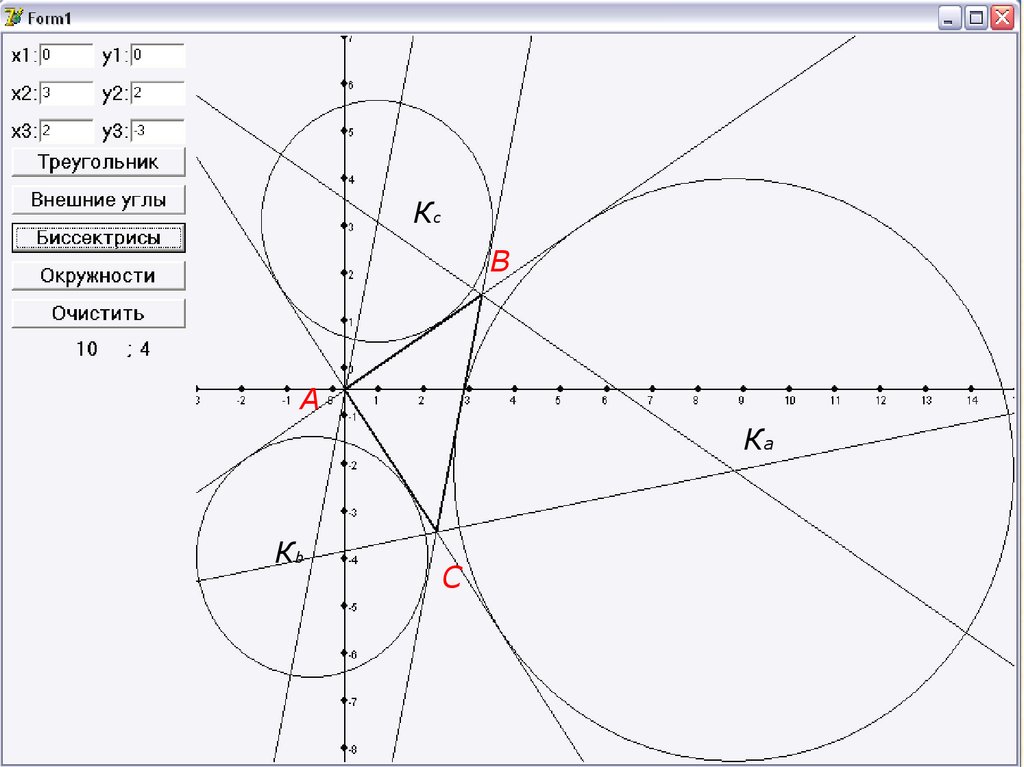
Кc
В
А
Ка
Кb
С

7.

1.2. СВОЙСТВА
ВНЕВПИСАННОЙ ОКРУЖНОСТИ
Центр вневписанной окружности
треугольника есть точка пересечения биссектрисы
внутреннего угла, противолежащего той стороне
треугольника, которой окружность касается, и биссектрис
двух внешних углов треугольника.
Свойство
1:
В
Дано: ∆ АВС; окр. (О; r);
М, N, К – точки касания.
Доказать: О – точка пересечения биссектрис В,
КАС, NСА.
Доказательство: Окружность касается сторон САК,
то центр окружности О равноудален от сторон этого угла,
следовательно, он лежит на биссектрисе САК. Аналогично,
точка О лежит на биссектрисе АСN. Т. к. окружность
касается прямых ВА и ВС, то она вписана в АВС, а значит
её центр лежит на биссектрисе АВС.
А
М
К
С
N
О

8. Свойство 2. Расстояния от вершины угла треугольника до точек касания вневписанной окружности со сторонами этого угла равны

1.2. СВОЙСТВА
ВНЕВПИСАННОЙ ОКРУЖНОСТИ
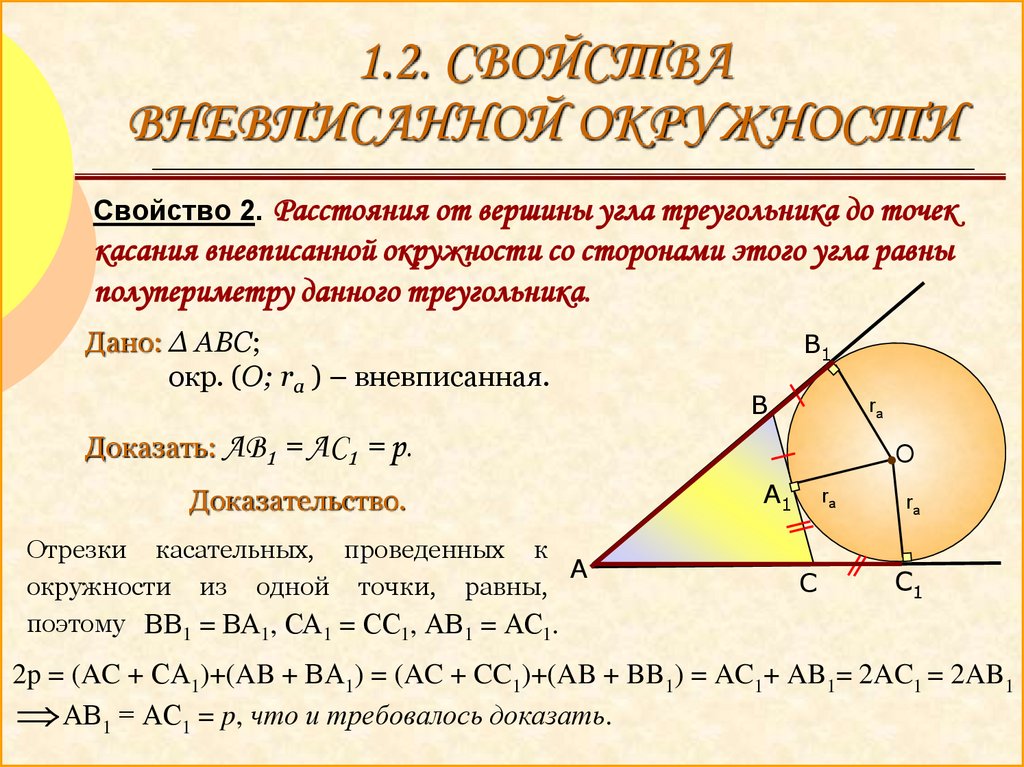
Свойство 2. Расстояния от вершины угла треугольника до точек
касания вневписанной окружности со сторонами этого угла равны
полупериметру данного треугольника.
Дано: ∆ АВС;
окр. (О; ra ) – вневписанная.
В1
В
ra
Доказать: АВ1 = АС1 = p.
Доказательство.
Отрезки касательных, проведенных к
А
окружности из одной точки, равны,
поэтому ВВ1 = ВА1, СА1 = СС1, АВ1 = АС1.
О
А1
ra
ra
С
2p = (AC + СА1)+(AB + ВА1) = (AC + CC1)+(AB + BB1) = AC1+ AB1= 2AC1 = 2AB1
АВ1 = АС1 = p, что и требовалось доказать.

9. Свойство 3. Радиус вневписанной окружности, касающейся сторон данного внутреннего угла треугольника, равен произведению

1.2. Свойства вневписанной окружности.
НЕКОТОРЫЕ СООТНОШЕНИЯ С РАДИУСАМИ ВНЕВПИСАННЫХ ОКРУЖНОСТЕЙ
Свойство 3. Радиус вневписанной окружности, касающейся сторон
данного внутреннего угла треугольника, равен произведению
полупериметра треугольника на тангенс половины этого угла, т.е.
ra p tg
2
, rb p tg
, rc p tg .
2
2
В
Дано: ∆ АВС;
окр. (О; ra ) – вневписанная.
Доказать: ra p tg
2
Доказательство.
В1
ra
ra
А1
.
Пусть САВ = .
∆ АОС1 – прямоугольный ОС1=АС1 tg
2
С
2
Остальные формулы выводятся аналогично.
О
ra
А
.
p
ra p tg
2
.

10. Свойство 4. Радиус вневписанной окружности, касающейся данной стороны треугольника, равен отношению площади треугольника к

1.2. Свойства вневписанной окружности.
НЕКОТОРЫЕ СООТНОШЕНИЯ С РАДИУСАМИ ВНЕВПИСАННЫХ ОКРУЖНОСТЕЙ
Свойство 4. Радиус вневписанной окружности, касающейся данной
стороны треугольника, равен отношению площади треугольника к
разности полупериметра и этой стороны.
Дано: ∆ АВС;
окр. (О; ra) – вневписанная.
S
S
S
.
r
,
r
,
Доказать: r a
c
b
p a
p b
В
c
p с
ra
а
А
ra
.
О
ra
Доказательство.
Имеем: S = S∆ABC = S∆AOC + S∆АOB – S∆BOC ,
С
С1
S
1
b c a 2a
r
.
S ra b c a ra
ra p a
a
p a
2
2
Аналогично выводятся остальные формулы.

11.

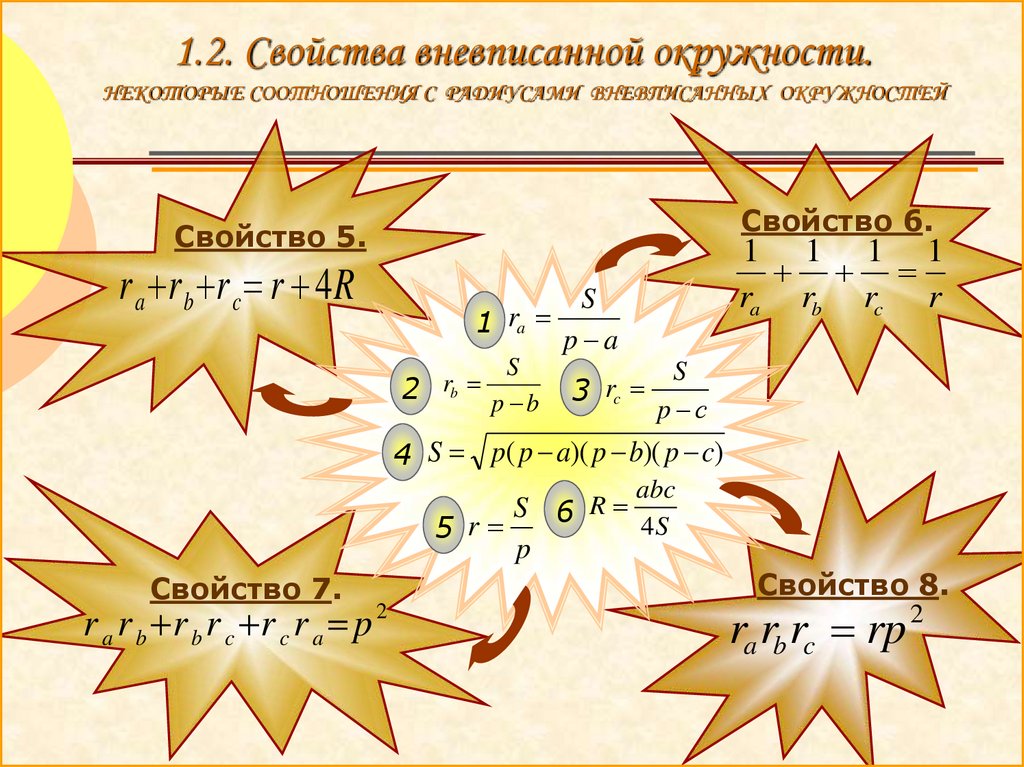
1.2. Свойства вневписанной окружности.
НЕКОТОРЫЕ СООТНОШЕНИЯ С РАДИУСАМИ ВНЕВПИСАННЫХ ОКРУЖНОСТЕЙ
Свойство 6.
Свойство 5.
r a r b r c r 4R
1 ra
S
r
b
2
p b
1 1 1 1
ra rb rc r
S
p a
3 rc
S
p с
4 S p( p a)( p b)( p c)
abc
S 6 R
4S
5 r
p
Свойство 7.
r a r b r b r c r c r a p 2
Свойство 8.
ra rb rc rp 2

12.

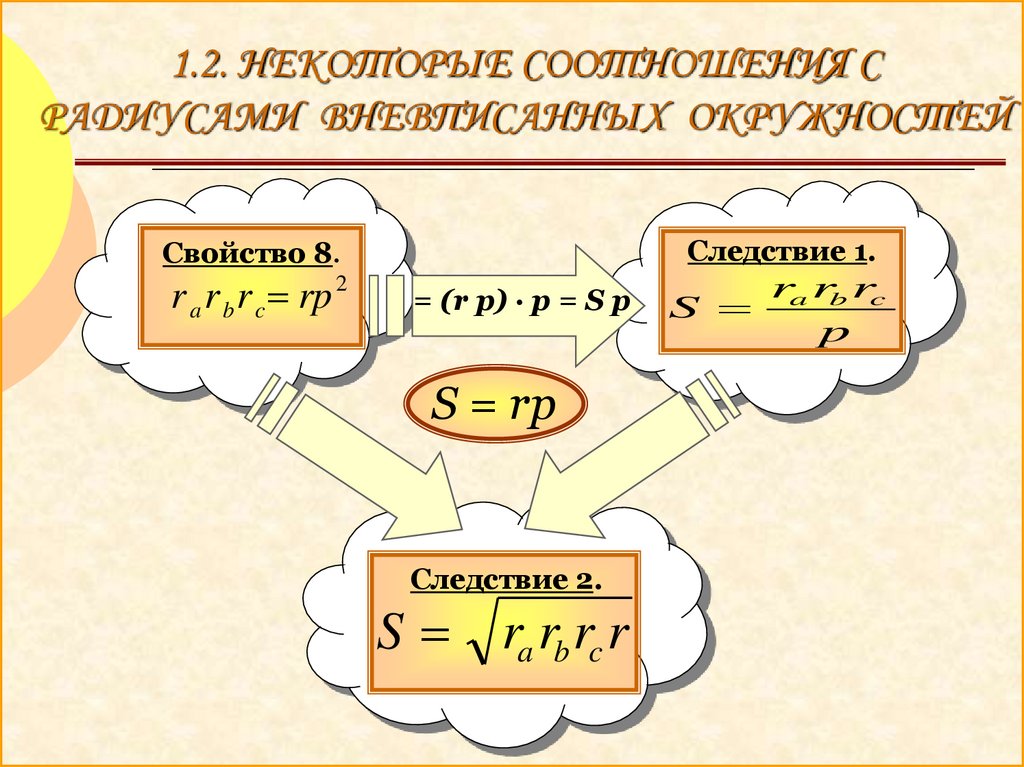
1.2. НЕКОТОРЫЕ СООТНОШЕНИЯ С
РАДИУСАМИ ВНЕВПИСАННЫХ ОКРУЖНОСТЕЙ
Следствие 1.
Свойство 8.
r a r b r c rp 2
= (r p) · p = S p
S = rp
Следствие 2.
S ra rb rc r
S
ra rb rc
p

13.

2.1. ПРИМЕНЕНИЕ СВОЙСТВ ВНЕВПИСАННЫХ
ОКРУЖНОСТЕЙ ПРИ РЕШЕНИИ ЗАДАЧ
Задача 1. Из точки А к данной
окружности проведены касательные
АТ1 и АТ2. К окружности проведена
касательная, пересекающая отрезки
АТ1 и АТ2 в точках В и С. Докажите,
что периметр ∆ABC не зависит от
положения касательной.
Запомнить: Р=2∙АТ1.
Решение. По свойству 2: р = АТ1.
Значит, независимо от положения
касательной, периметр ∆ ABC равен
удвоенной длине отрезка АТ1.
Р=2∙АТ1.

14.

Правильному применению методов можно научиться,
только применяя их на разнообразных примерах.
Г. Цейтен
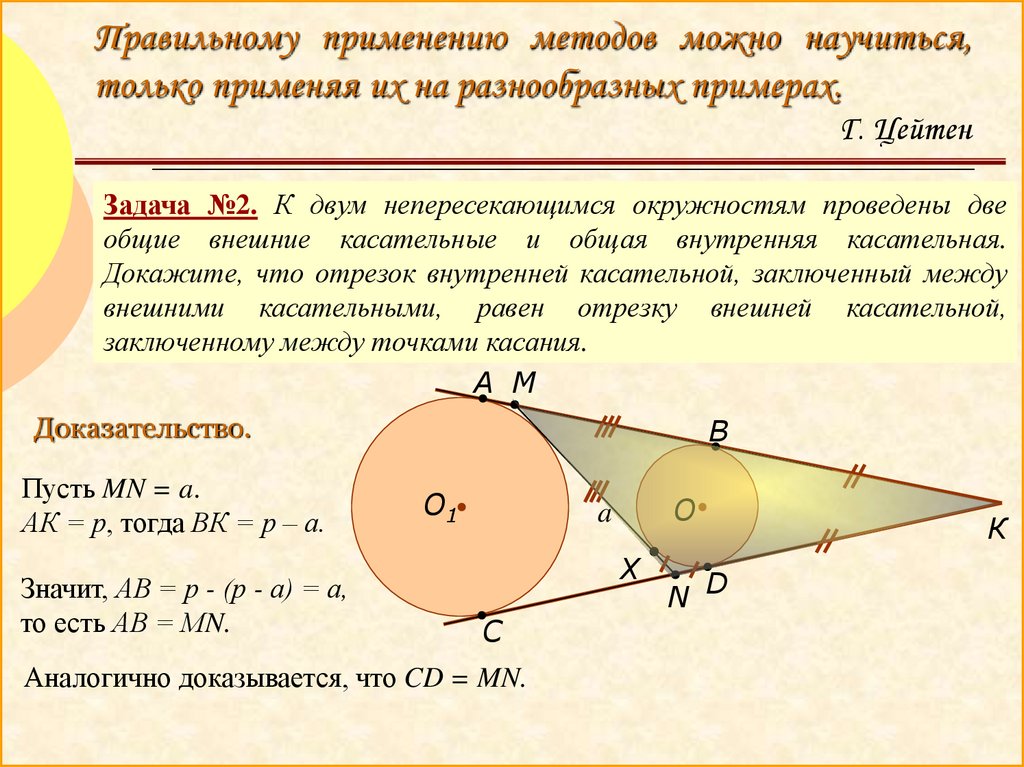
Задача №2. К двум непересекающимся окружностям проведены две
общие внешние касательные и общая внутренняя касательная.
Докажите, что отрезок внутренней касательной, заключенный между
внешними касательными, равен отрезку внешней касательной,
заключенному между точками касания.
А М
Доказательство.
Пусть MN = a.
АК = р, тогда ВК = р – а.
Значит, АВ = р - (р - а) = а,
то есть АВ = МN.
В
О1
О
a
X
С
Аналогично доказывается, что CD = MN.
N D
К

15.

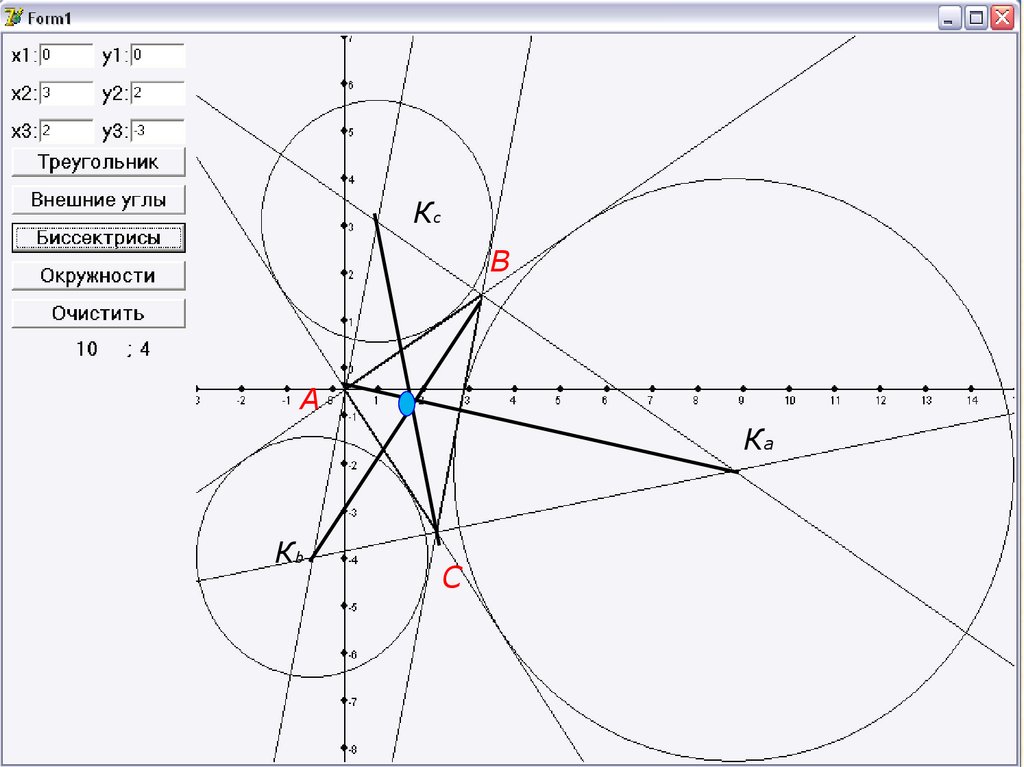
Кc
В
А
Ка
Кb
С

16.

2.1. ПРИМЕНЕНИЕ СВОЙСТВ ВНЕВПИСАННЫХ
ОКРУЖНОСТЕЙ ПРИ РЕШЕНИИ ЗАДАЧ
Задача №3. В ∆ ABC проведены биссектрисы AL1 и BL2. Найдите
A, если известно, что L1L2 - биссектриса угла AL1C.
Решение.
Точка L2 по условию лежит на
пересечении биссектрисы
внутреннего AВС и биссектрисы
внешнего угла AL1C треугольника
∆ABL1. Значит, точка L2 является
центром вневписанной окружности
∆ ABL1. Следовательно, AL2 биссектриса внешнего А
треугольника ∆ABL1.
Значит, А= 120°.
Ответ: 120º.

17.

2.1. ПРИМЕНЕНИЕ СВОЙСТВ ВНЕВПИСАННЫХ
ОКРУЖНОСТЕЙ ПРИ РЕШЕНИИ ЗАДАЧ
Задача 4.(сборник ЕГЭ-2014, под редакцией Ф.Ф.Лысенко). Найдите
произведение радиусов всех вневписанных окружностей треугольника со
сторонами 4,5,6.
Решение: По свойству 8: rarbrc = rp2.
r-радиус вписанной в треугольник окружности,
р – полупериметр треугольника.
Периметр треугольника Р = 4+5+6=15, р = 15/2.
r = S/p. Площадь найдем по формуле Герона:
S =√р(p−a)(p−b)(p−a). S = √7,5(7,5-4)(7,5-5)(7,5-6) = 3,75√7;
r =3,75 √7 : 7,5=√7/2. Отсюда, rarbrc = (√7/2) :(15/2)² =
=225 √7/8

18.

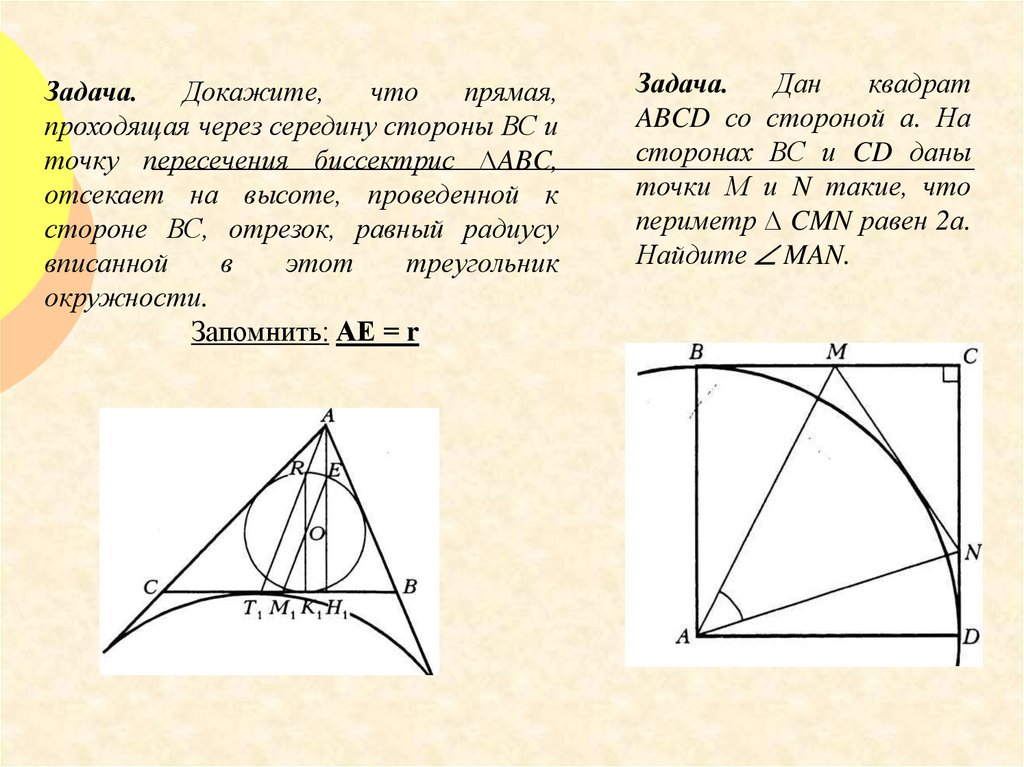
Задача.
Докажите,
что
прямая,
проходящая через середину стороны ВС и
точку пересечения биссектрис ∆ABC,
отсекает на высоте, проведенной к
стороне ВС, отрезок, равный радиусу
вписанной
в
этот
треугольник
окружности.
Запомнить: АЕ = r
Задача.
Дан
квадрат
ABCD со стороной а. На
сторонах ВС и CD даны
точки М и N такие, что
периметр ∆ CMN равен 2а.
Найдите MAN.

19.

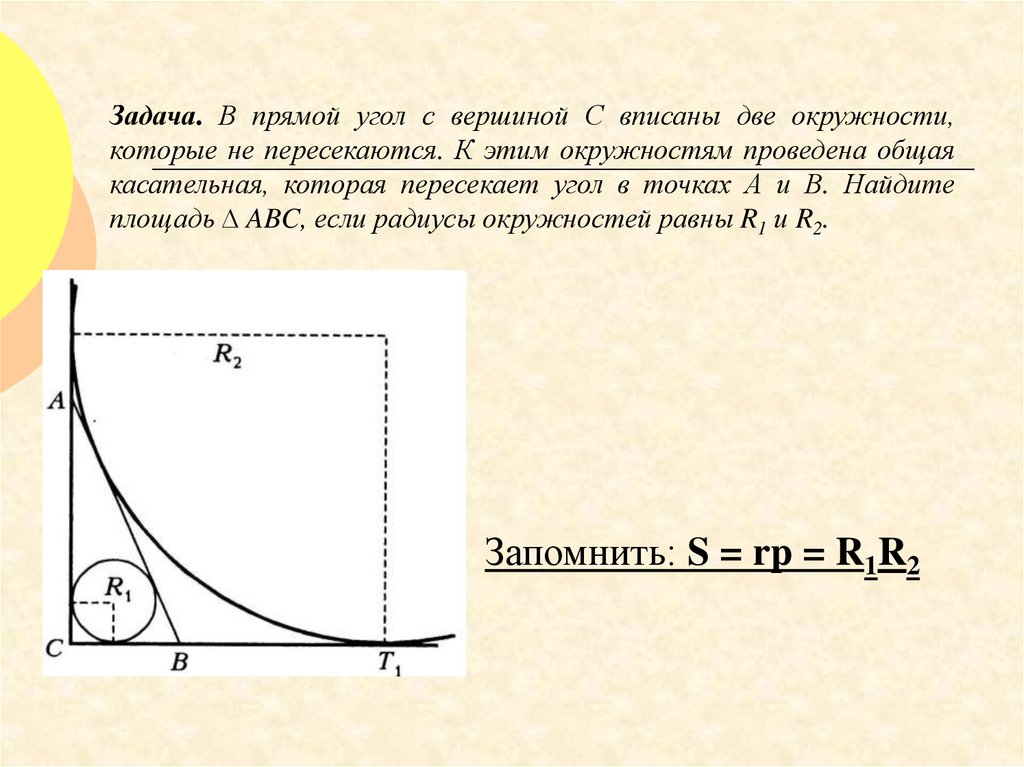
Задача. В прямой угол с вершиной С вписаны две окружности,
которые не пересекаются. К этим окружностям проведена общая
касательная, которая пересекает угол в точках А и В. Найдите
площадь ∆ ABC, если радиусы окружностей равны R1 и R2.
Запомнить: S = rp = R1R2

20.

Задача. Основание АС равнобедренного треугольника равно 10.
Окружность радиуса 7,5 с центром вне этого треугольника касается
продолжения боковых сторон треугольника и касается основания АС
в его середине. Найдите радиус окружности вписанной в треугольник
АВС.
Мальцев Д.А. « Математика. Все для ЕГЭ-2011» НИИ школьных
технологий , 2011г.
А
В
F
D
O
r К
С

21. 4. Заключение

В результате проведённого исследования:
рассмотрены свойства вневписанных окружностей;
установлена связь между радиусами вневписанных
окружностей и полупериметром треугольника, между
радиусами вписанной, описанной и вневписанных
окружностей;
выявлена зависимость площади треугольника от
радиусов вневписанных окружностей и полупериметра;
разработан комплекс задач по данной теме.

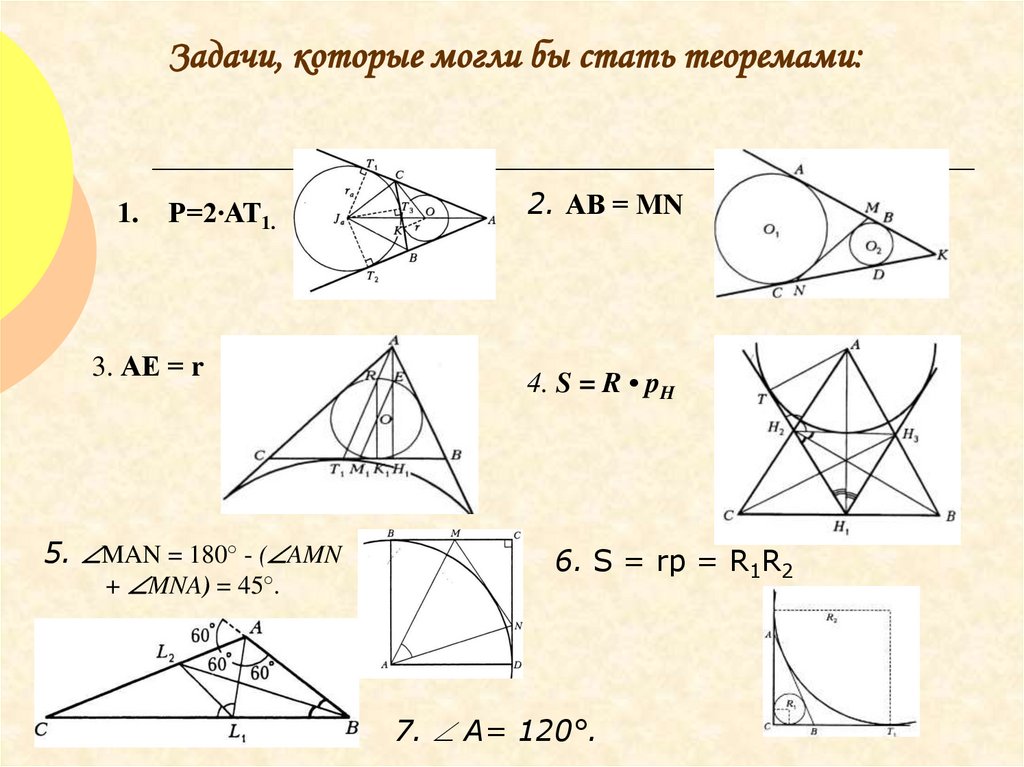
22.

Задачи, которые могли бы стать теоремами:
1.
Р=2∙АТ1.
3. АЕ = r
5. MAN = 180° - ( AMN
+ MNA) = 45°.
2. АВ = MN
4. S = R • pH
6. S = rp = R1R2
7. А= 120°.

23.

Научно-практическая конференция