Похожие презентации:
Окружность и ее элементы. Геометрия. 9 класс
1. Геометрия 9 класс
Окружность и ее элементы2. Содержание
Основные понятия
Свойства вписанных углов
Углы, связанные с окружностью
Отрезки, связанные с окружностью
Теорема Птолемея
Окружность, вписанная в многоугольник
Окружность, описанная около многоугольника
Вневписанная окружность
3. Основные понятия
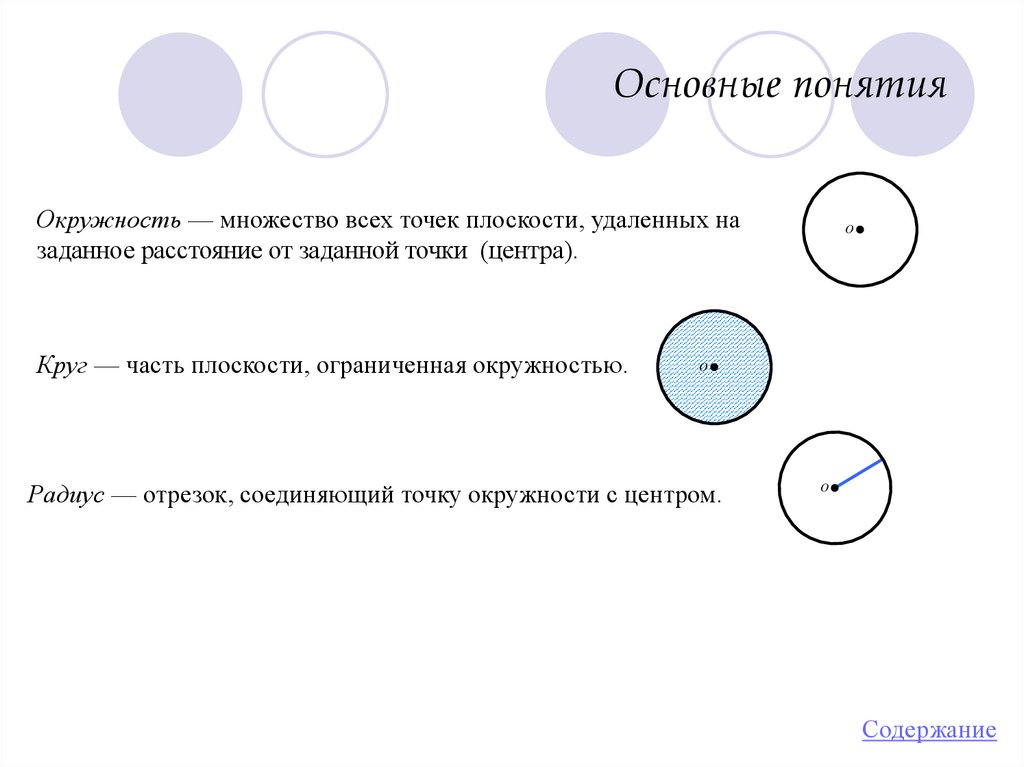
Окружность — множество всех точек плоскости, удаленных назаданное расстояние от заданной точки (центра).
Круг — часть плоскости, ограниченная окружностью.
O
O
Радиус — отрезок, соединяющий точку окружности с центром.
O
Содержание
4. Основные понятия
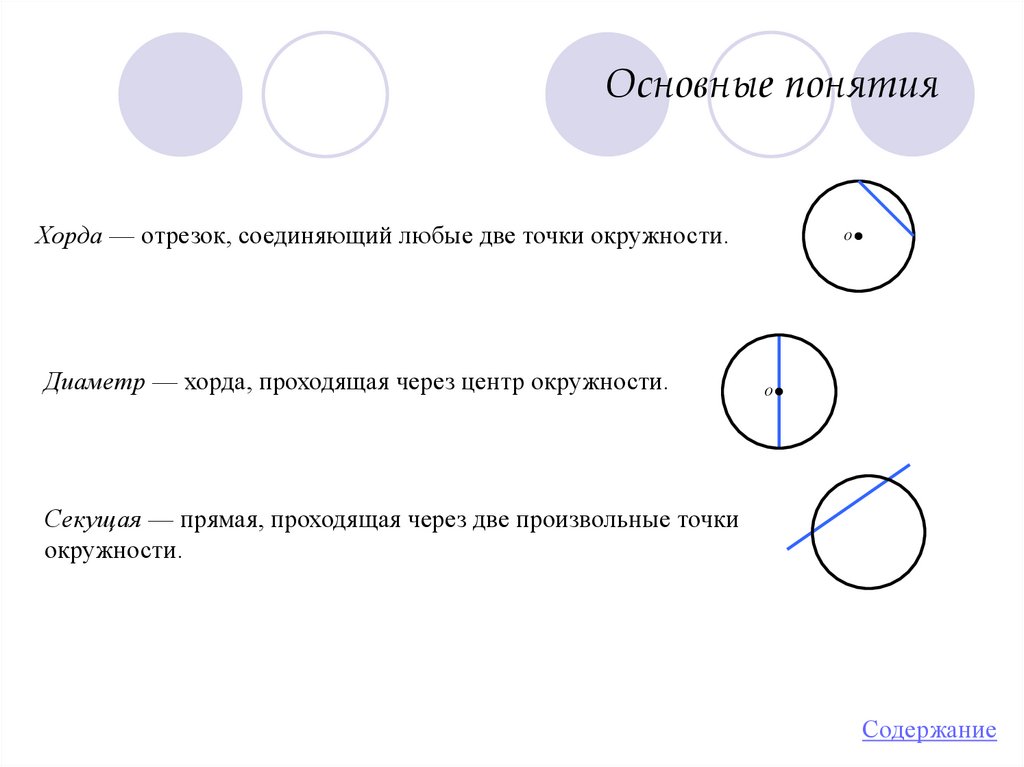
Хорда — отрезок, соединяющий любые две точки окружности.Диаметр — хорда, проходящая через центр окружности.
O
O
Секущая — прямая, проходящая через две произвольные точки
окружности.
Содержание
5. Основные понятия
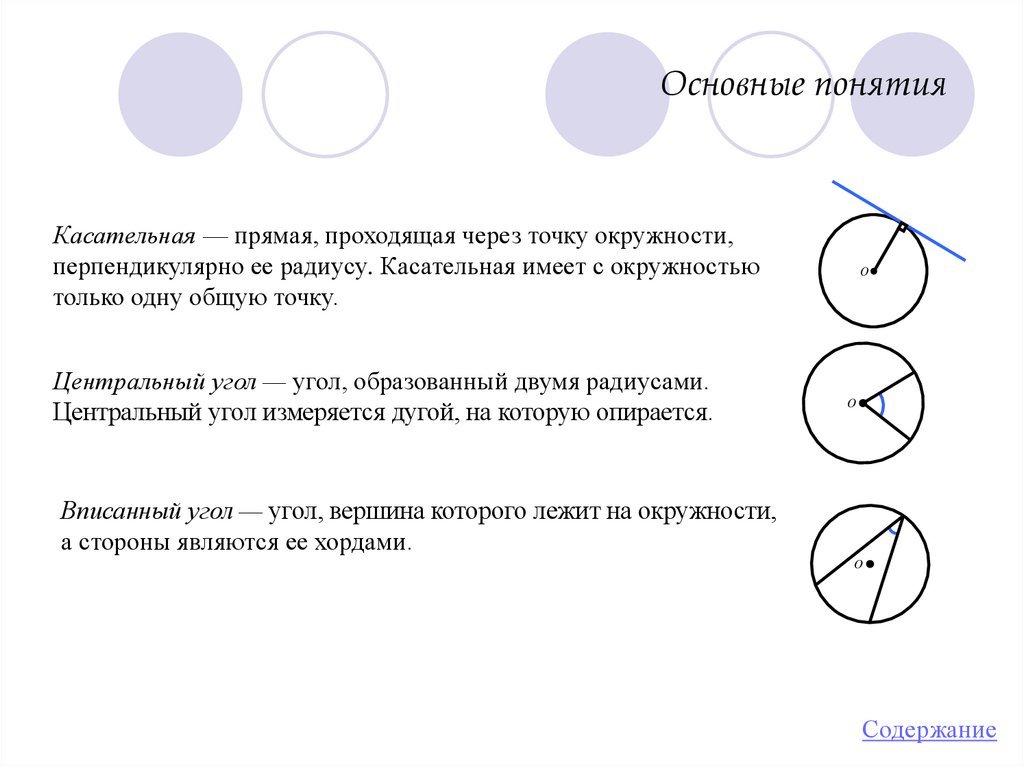
Касательная — прямая, проходящая через точку окружности,перпендикулярно ее радиусу. Касательная имеет с окружностью
только одну общую точку.
Центральный угол — угол, образованный двумя радиусами.
Центральный угол измеряется дугой, на которую опирается.
O
O
Вписанный угол — угол, вершина которого лежит на окружности,
а стороны являются ее хордами.
O
Содержание
6. Свойства вписанных углов
1. Вписанный угол измеряется половиной дуги, на которую он опирается.Доказательство.
1) Центр на одной из сторон.
B
ABC — вписанный угол, BA и BC — хорды, OA — радиус.
Проведем радиус OA. Рассмотрим треугольник OAB:
OB OA
O
A
Следовательно, он равнобедренный иA B
Угол AOC — внешний, следовательно,
AOC A B 2 B
C
Следовательно,
1
B AOC
2
Угол AOC измеряется дугой AC, следовательно, его половина измеряется половиной дуги AC.
Что и требовалось доказать.
Содержание
7. Свойства вписанных углов
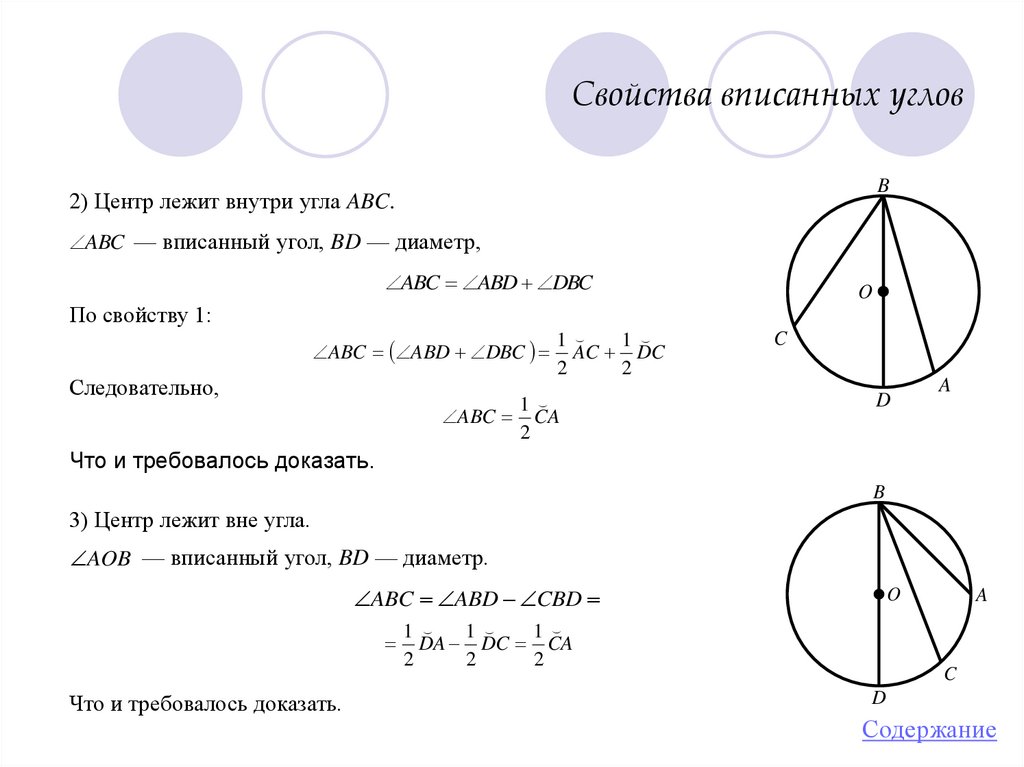
B2) Центр лежит внутри угла ABC.
ABC — вписанный угол, BD — диаметр,
ABC ABD DBC
По свойству 1:
ABC ABD DBC
Следовательно,
1
1
AC DC
2
2
1
ABC CA
2
O
C
D
A
Что и требовалось доказать.
B
3) Центр лежит вне угла.
AOB — вписанный угол, BD — диаметр.
ABC ABD CBD
Что и требовалось доказать.
O
1
1
1
DA DC CA
2
2
2
A
C
D
Содержание
8. Свойства вписанных углов
2. Вписанные углы, опирающиеся на одну и ту же дугу, равны.Доказательство.
и — вписанные углы, KL — дуга.
По свойству 1:
Следовательно,
1
KL
2
1
KL
2
O
K
L
Что и требовалось доказать.
Содержание
9. Свойства вписанных углов
3. Вписанный угол, опирающийся на диаметр — прямой.A
Доказательство.
— внутренний угол, BC — диаметр.
По свойству 1:
B
O
C
1
BC
2
Так как BC — полуокружность, следовательно, BC 180
Таким образом,
1
1
BC 180 90
2
2
Что и требовалось доказать.
Содержание
10. Свойства вписанных углов
4. Равные дуги окружности стягиваются равными хордами.Доказательство.
AB CD , AB и CD — хорды.
A
O
1. Проведем радиусы R OA OB OC OD
2. Треугольники OAB и OCD равны, т.к.
B
C
D
OA OB OC OD (радиусы).
BOA
Следовательно,
1
1
AB и DOC DC
2
2
BOA DOC
В равных треугольниках против соответственно равных углов лежат равные стороны,
следовательно, AB CD
Что и требовалось доказать.
Содержание
11.
Углы, связанные с окружностьюТеорема (угол между пересекающимися хордами). Угол между двумя пересекающимися
хордами равен полусумме высекаемых ими дуг.
A B
B A
A
2
O B
Доказательство.
2
Угол — внешний угол треугольника DOB.
B A
2
C
B
A
2
D
Что и требовалось доказать.
Содержание
12.
Углы, связанные с окружностьюТеорема (угол между секущими). Угол между двумя секущими, проведенными из одной
точки, равен полуразности большей и меньшей высекаемых ими дуг.
A B
2
M
A
Доказательство.
B
2
По теореме о внешнем угле треугольника MBC:
A
B
A B
2
2
2
Что и требовалось доказать.
B
B
A
2
C
A
D
Содержание
13.
Углы, связанные с окружностьюТеорема (угол между касательной и хордой, проведенной через точку касания).
Угол между касательной и хордой, проведенной в точку касания, равен половине дуги,
стягиваемой этой хордой.
A
Доказательство.
1. Проведем диаметр.
2. Угол
опирается на дугу A
2
Тогда,
1
A
A
( A)
2
2
2
2 2
2
B
O
2
A
A
Что и требовалось доказать.
Аналогично для тупого угла
Содержание
14.
Углы, связанные с окружностьюТеорема (угол между касательной и секущей). Угол между касательной и секущей равен
полуразности высекаемых ими дуг.
Доказательство.
C
1
По теореме о вписанных углах: A
2
.
1
По теореме об угле между касательной и хордой B
2
— внешний угол треугольника ABM.
A
B
B
A
1 1
A B
A B
2
2
2
Что и требовалось доказать.
Содержание
M
15.
Углы, связанные с окружностьюТеорема (угол между касательными). Угол между двумя касательными, проведенными из
одной точки, равен полуразности большей и меньшей высекаемых ими дуг.
Доказательство.
Проведем радиусы в точки касания, они перпендикулярны
касательным.
90 90 B 360 180 B
Примечание.
Тогда
A
B
B
A B
180
2
A B A B
B
2
2
Что и требовалось доказать.
Содержание
16.
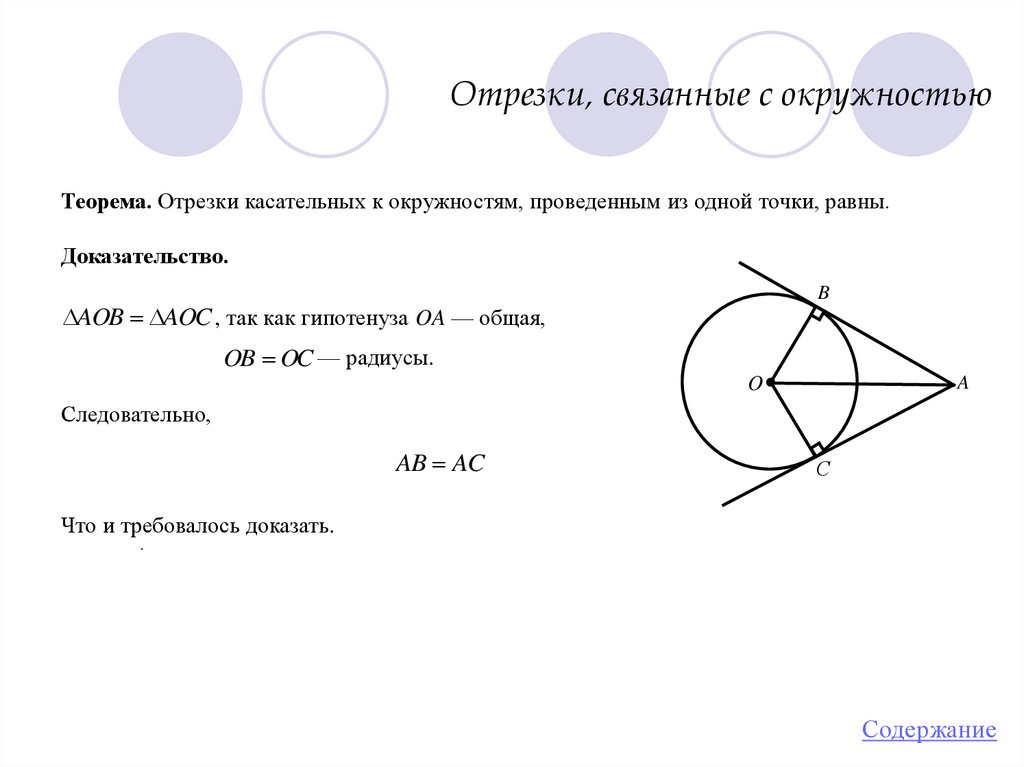
Отрезки, связанные с окружностьюТеорема. Отрезки касательных к окружностям, проведенным из одной точки, равны.
Доказательство.
B
AOB AOC , так как гипотенуза OA — общая,
OB OC — радиусы.
A
O
Следовательно,
AB AC
С
Что и требовалось доказать.
.
Содержание
17.
Отрезки, связанные с окружностьюТеорема. Произведение отрезков, на которые делится хорда данной точкой, есть для данной
окружности величина постоянная.
ab cd
A
Доказательство.
Пусть AB и CD — данные хорды, O — точка пересечения.
Проведем хорды AC и BD.
D
a
c
O
d
b
C
B
AOC ~ DOB , так как AOC DOB — вертикальные,
CAB CDB — опираются на дугу CB.
Тогда
a c
ab cd
d b
Что и требовалось доказать.
Содержание
18.
Отрезки, связанные с окружностьюТеорема. Произведение секущей на ее внешнюю часть есть для данной окружности величина
постоянная.
( a b ) b (c d ) d
Доказательство.
Проведем хорды AC и BD.
A
a
B
AMC ~ DMB (по двум углам):
AMD — общий,
D
d
C
b
c
M
MAC BDC — опираются на дугу BC.
Тогда
b
c
( a b ) b (c d ) d
c d a b
Что и требовалось доказать.
Содержание
19.
Отрезки, связанные с окружностьюТеорема. Квадрат касательной равен произведению секущей на ее внешнюю часть.
c 2 a (a b)
M
с
K
a
Доказательство.
MKB ~ MAK, так как KMA — общий,
MKB KAB
B
1
KB
2
b
A
Тогда
c
a
c 2 a ( a b)
a b c
Что и требовалось доказать.
Содержание
20.
Отрезки, связанные с окружностьюТеорема. Отношение хорды к синусу вписанного угла, который на нее опирается,
равно двум радиусам (теорема синусов).
A
Доказательство.
A
R
A A , так как они опираются на одну дугу BC.
R
a
a
2R
sin A sin A
a
B
С
Что и требовалось доказать.
Содержание
21.
Теорема ПтолемеяТеорема. Во всяком четырехугольнике, вписанном в окружность, сумма произведений длин
противоположных сторон равна произведению длин его диагоналей.
C
AC BD AB CD AD BC
Доказательство.
1. Проведем диагонали AC и BD.
2. Выберем на диагонали BD точку K так, чтобы BAK CAD
B
3. Тогда треугольники KBA и ACD подобны (по равному по построению A
углу и по углу, опирающемуся на дугу AD); треугольники AKD и ABC
подобны (по двум углам: BAC KAD (по построению) и BDA BCA).
4. Тогда:
K
D
| BK | | CD |
| BA | | AC |
| BK | | AC | | CD | | BA |
|
AD
|
|
AC
|
|
AD
|
|
BC
|
|
AC
|
|
KD
|
| KD | | BC |
| AC | (| BK | | KD |) | AB | | CD | | AD | | BC |
| AC | | BD | | AB | | CD | | AD | | BC |
Что и требовалось доказать.
Содержание
22.
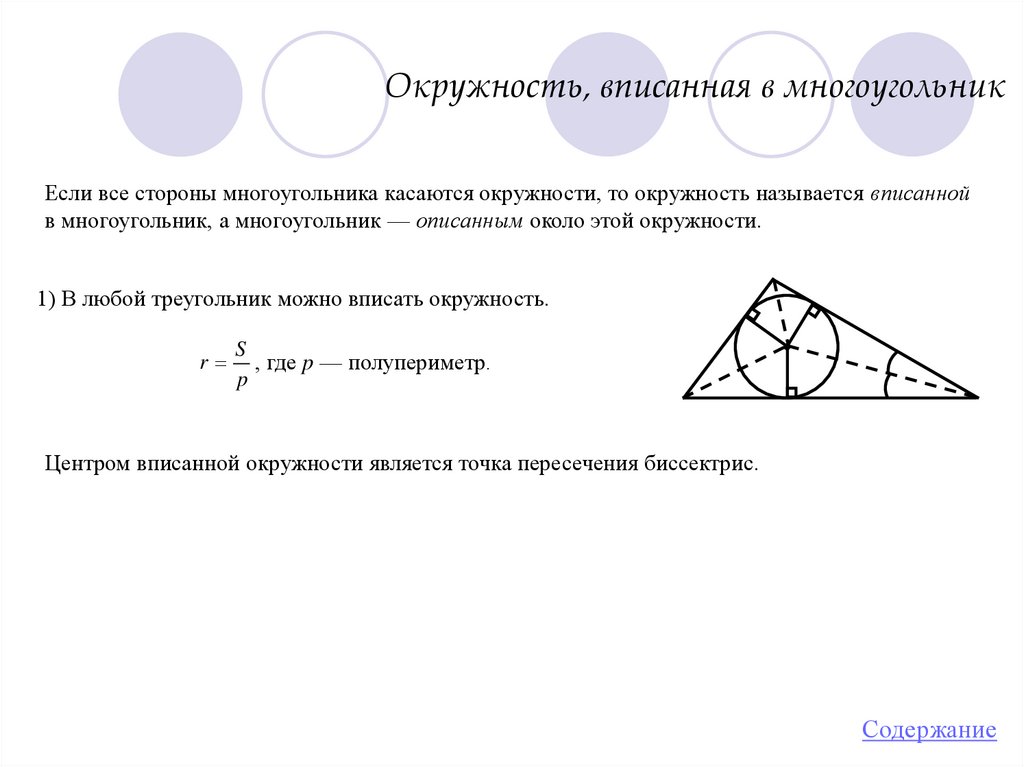
Окружность, вписанная в многоугольникЕсли все стороны многоугольника касаются окружности, то окружность называется вписанной
в многоугольник, а многоугольник — описанным около этой окружности.
1) В любой треугольник можно вписать окружность.
r
S
, где p — полупериметр.
p
Центром вписанной окружности является точка пересечения биссектрис.
Содержание
23.
Окружность, вписанная в многоугольник2) В любом описанном четырехугольнике суммы противоположных сторон равны.
a
d
d
AK AL , так как AK и AL — касательные к окружности,
проведенные из одной точки.
Аналогично с остальными отрезками.
b
b
L
a
K
c
c A
Тогда сумма противоположных сторон есть для данного четырехугольника величина
постоянная.
Содержание
24.
Окружность, вписанная в многоугольник3) Если суммы противоположных сторон выпуклого четырехугольника равны, то в него
можно вписать окружность.
Из параллелограммов окружность можно вписать в ромб, квадрат.
Если в трапецию вписана окружность, то сумма оснований равна сумме боковых сторон,
а средняя линия — полусумме боковых сторон.
a
m
a b c d
2
2
c
m
d
b
Содержание
25.
Окружность, описанная около многоугольникаЕсли вершины многоугольника лежат на окружности, то окружность называется описанной
около многоугольника, а многоугольник — вписанным в эту окружность.
1) Около любого треугольника можно описать окружность.
C
B
4S
R
abc
O
S 2 R 2 sin sin sin
A
Центром описанной окружности является точка пересечения серединных перпендикуляров к
сторонам.
Содержание
26.
Окружность, описанная около многоугольника2) В любом четырехугольнике, вписанном в окружность, сумма противоположных углов равна 180°.
A
С
1
BCD
2
B
A
1
DAB
2
Тогда
A C
1
( BCD DAB) 180
2
C
D
Из всех параллелограммов окружность можно описать около прямоугольника, квадрата.
Содержание
27. Вневписанная окружность
Вневписанная окружность — окружность, касающаяся одной стороны треугольника ипродолжения двух других его сторон.
Теорема. Расстояние от вершины треугольника до точки касания вневписанной окружности с
продолжением его боковой стороны равно полупериметру p.
A
с
b
С
a B
Доказательство.
N
H
M
1. | AN | | AM | — отрезки касательных, исходящих из одной точки.
| CH | | CN | , | HB | | BM |
2. P | AC | | CH | | AB | | HB | | AN | | AM | 2 | AN |
Таким образом, | AN | p
Примечание: точка касания вневписанной окружности со стороной треугольника делит его
периметр пополам: | AC | | CH | p
Следствие:
| CH | p | AC | p c
| HB | p b
.
Содержание
28. Вневписанная окружность
Теорема. Радиус вневписанной окружности, проведенный к стороне a, вычисляется по формуле:S
p a
ra
Доказательство.
A
C
1. Площадь четырехугольника ONAM:
1
1
SONAM S AOM S AON ra | AM | ra | AN |
2
2
ra | AM | p ra
B
H
N
ra
M
O
2. Площадь четырехугольника ONAM:
SONAM S ABC SOMBCN S ABC 2S BOH 2SCHO
1
S ABC 2SBOC S ABC 2 ra a S ABC ra a
2
3. Таким образом,
.
ra p S ABC ra a ra ( p a) S ABC ra
Что и требовалось доказать.
S ABC
p a
Содержание
29. Вневписанная окружность
Теорема. Площадь треугольника можно вычислить по формуле:S ra rb rc r
Доказательство.
ra rb rc r
S
S
S S
p a p b p c p
S4
S4
ra rb rc r
ra rb rc r 2
p( p a)( p b)( p c)
S
ra rb rc r S 2 S ra rb rc r
Что и требовалось доказать.
Содержание
30.
КонецНачать заново
Завершить показ
























 Математика
Математика








