Круги Эйлера. Леонард Эйлер

1.

Круги Эйлера
Презентация подготовлена:
Никонова С.Г., учитель математики

2.

Леонард Эйлер
Леонард Эйлер
(1707 – 1783)
Последние 17 лет жизни Эйлера были омрачены почти полной потерей зрения. Но он
продолжал творить так же интенсивно, как в молодые годы. Только теперь он уже диктовал
ученикам, которые проводили за него громоздкие вычисления.
С1761 по 1768 год им были написаны знаменитые «Письма к немецкой принцессе», где
Эйлер как раз и рассказывал о своем методе, об изображении множеств в виде кругов.
Именно поэтому рисунки в виде кругов, обычно называют «кругами Эйлера». Эйлер отмечал,
что изображение множеств в виде кругов «очень подходит для того, чтобы облегчить наши
рассуждения». Понятно, что слово «круг» здесь весьма условно, множества могут
изображаться на плоскости в виде произвольных фигур.
После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781
– 1848). Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы.
Методом кругов Эйлера пользовался и немецкий математик Эрнст Шредер (1841 – 1902).
Этот метод широко используется в его книге «Алгебра логика». Но наибольшего расцвета
графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923).
С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в
Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки
называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами
(или кругами) Эйлера – Венна.

3.

Решите задачу.
Все мои друзья занимаются
каким-либо видом спорта. 16 из
них увлекаются футболом, 12 –
баскетболом. И только двое
увлекаются и тем и другим видом
спорта. Скажите, пожалуйста,
сколько у меня друзей?
Решение.
14 + 2 + 10 = 26
Ответ: 26

4.

Решите задачу
Каждый из 35
шестиклассников берет
книги в одной из библиотек.
25 являются читателями
школьной библиотеки, а 20 –
районной. Сколько учеников
6 класса посещают обе
библиотеки?.
Решение.
(25 + 20) – 35 = 10
Ответ: 10

5.

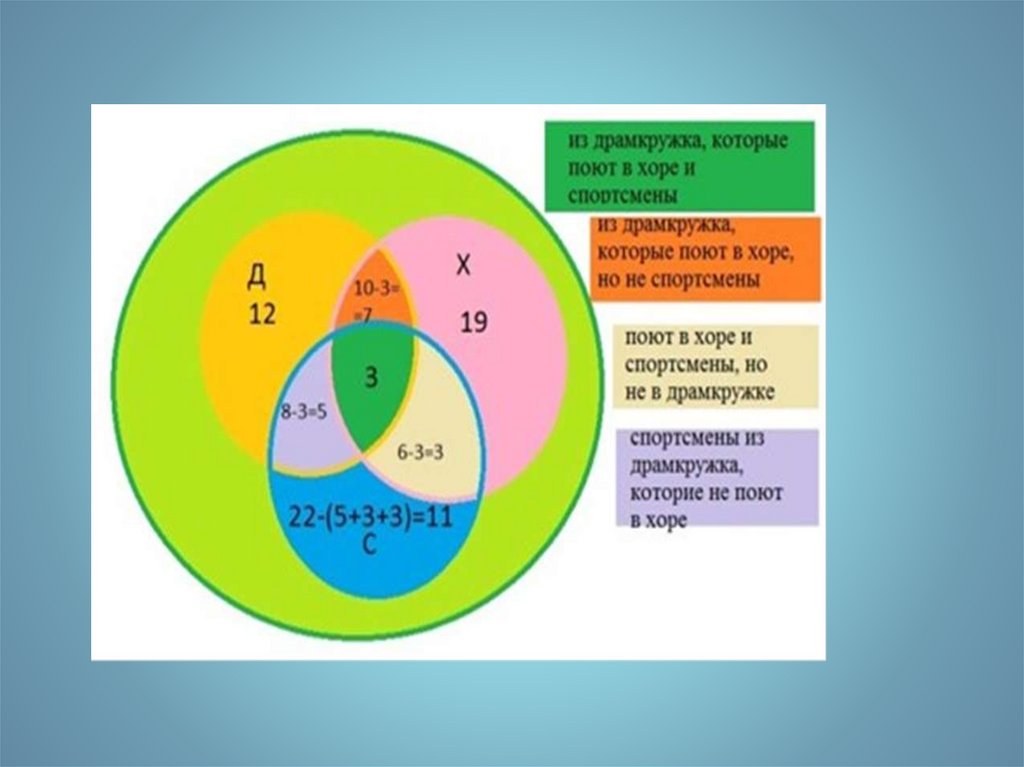
В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 –
троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и
троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя
видами транспорта?

6.

7.

1 способ.
Для решения опять воспользуемся кругами Эйлера. Пусть х человек пользуется всеми тремя
видами
транспорта.
Тогда
пользуются
только
метро
и
троллейбусом
–
(10
–
х)
человек,
только
автобусом
и
троллейбусом
–
(9
–
х)
человек,
только метро и автобусом – (12 – х) человек.
Найдем,
сколько
человек
20 – (12 – х) – (10 – х) – х = х – 2.
пользуется
одним
только
метро:
Аналогично получаем: х – 6 – только автобусом и х + 4 – только троллейбусом, так как всего
30
человек,
составляем
уравнение:
х + (12 – х) + (9 – х) + (10 – х) + (х + 4) + (х – 2) + (х – 6) = 30,
отсюда х = 3.

8.

2 способ. А можно эту задачу решить задачу другим способом: 20 + 15 + 23 – 10 – 12 – 9 + х =
30, 27 + х = 30, х = 3. Здесь сложили количество учеников, которые пользуются хотя бы одним
видом транспорта и из полученной суммы вычли количество тех, кто пользуется двумя или
тремя видами и, поэтому, вошли в сумму 2-3 раза. Таким образом, получили количество всех
учеников в классе.
Ответ. 3 человека ежедневно пользуются всеми тремя видами транспорта.