Похожие презентации:
Тайна корней квадратного уравнения
1. Тайна корней квадратного уравнения
Подготовила : Никонова СветланаГеоргиевна, учитель математики
МОУ «Колосковская СОШ»
2. Цели :
• рассмотреть квадратные уравненияразличных типов;
• познакомить с алгоритмами устного
решения квадратных уравнений;
3. Решите уравнения:
а) х2 +2х -3 = 0;
б) х2 - 4х + 3 = 0;
в) х2 + 8х + 7 = 0;
г) х2 + 7х +6 = 0;
д) 5х2 + 7х – 12=0;
е) 6х2– 23х + 17=0;
ж) 10х2 + 21х – 31=0;
з) 4х2 – 13х + 9 = 0.
4. Корни уравнений:
а)
б)
в)
г)
д)
е)
ж)
з)
х1 = -3 ,
х1 = 1 ,
х1 = -7 ,
х1 = -6 ,
х1 = -2,4,
х1 = -17/6,
х1 = -3,1,
х1 =1 ,
х2 = 1;
х2 = 3;
х2 = -1;
х2 = -1;
х2 = 1;
х2 = 1;
х2 = -1;
х2 = 2,25.
5. Вывод:
• Если а + в +с = 0 , то х1 = 1; х2 = с/а• Если а + с = в , то х1 = -1; х2 = - с/а
6. Решите самостоятельно:
а ) х2 + 12х -13 = 0;
б) х2 - 11х + 10 = 0;
в) х2 + 17х – 18 = 0;
г) 5х2 – 7х + 2 = 0;
д) 3х2 + 4х + 1 = 0;
е) 7х2 + 9х + 16 = 0.
7. Решите уравнения :
• 1)2х2 + 5х + 2 = 0;
• 2)
6х2 + 37х + 6 = 0;
• 3)
4х2 + 17х + 4 = 0.
8. Корни уравнений:
• 1) х1 = -2 , х2 = -1/2;• 2) х1 = -6 , х2 = -1/6;
• 3) х1 = -4 , х2 = -1/4.
9. Вывод :
• Из этой серии квадратных уравненийнетрудно заметить и доказать (решая
уравнение с помощью дискриминанта), что
если ах2 + (а2 + 1)х + а = 0 , то
х1 = -а ; х2 = - 1/а
10. Решите уравнения:
• 1) 2х2 – 5х +2 = 0;• 2) 3х2 -10х +3 = 0;
• 3) 4х2 -17х + 4 = 0.
11. Корни данных уравнений:
• 1)х1 = 2 , х 2 = ½
• 2)
х1 = 3 , х2 = 1/3
• 3)
х1 = 4 , х2 = 1/4
12. Вывод:
• Из этой серии квадратных уравненийнетрудно заметить и доказать, что
если ах2 – ( а2 + 1)х + а = 0, то
х1 = а; х2 = 1/а
13. Решите уравнения:
• 1) 3х2 – 8х – 3 = 0;• 2) 4х2 – 15х -4 = 0;
• 3) 5х2 – 24х – 5 = 0.
14. Корни уравнений:
• 1) х1 = 3 , х2 = - 1/3;• 2) х1 = 4 , х2 = -1/4;
• 3) х1 = 5 , х2 = -1/5.
15. Вывод:
• Из этой серии квадратных уравненийнетрудно заметить и доказать, что
если ах2 – ( а2 - 1)х – а = 0, то
х1 = а ; х2 = -1/а
16. Решите уравнения:
• 1) 3х2 + 8х – 3 = 0;• 2) 4х2 + 15х – 4 = 0;
• 3) 5х2 + 24х – 5 = 0.
17. Корни уравнений:
• 1) х1 = -3 , х2 = 1/3;• 2) х1 = -4 , х2 = 1/4;
• 3) х1 = -5 , х2 = 1/5.
18. Вывод:
• Из этой серии квадратных уравненийнетрудно заметить и доказать, что
если ах2 + ( а2 - 1)х – а = 0, то
х1 = - а ; х2 = 1/а
19. Составьте уравнения, корни которых равны:
• 1) - 1/7 и 7;• 2)
1/8 и 8;
• 3)
1/9 и -9;
• 4)
-1/2 и -2.
20. Решите самостоятельно:
1) 13х2 + 168х -13 = 0;
2) 8х2 + 63х – 8 = 0;
3) 10х2 – 99х – 10 = 0;
4) 12х2 – 143х – 12 = 0;
5) 5х2 – 26х + 5 = 0;
6) 7х2 – 50х + 7 = 0;
7) 9х2 + 82х + 9 = 0;
8) 11х2 + 122х + 11 =0.







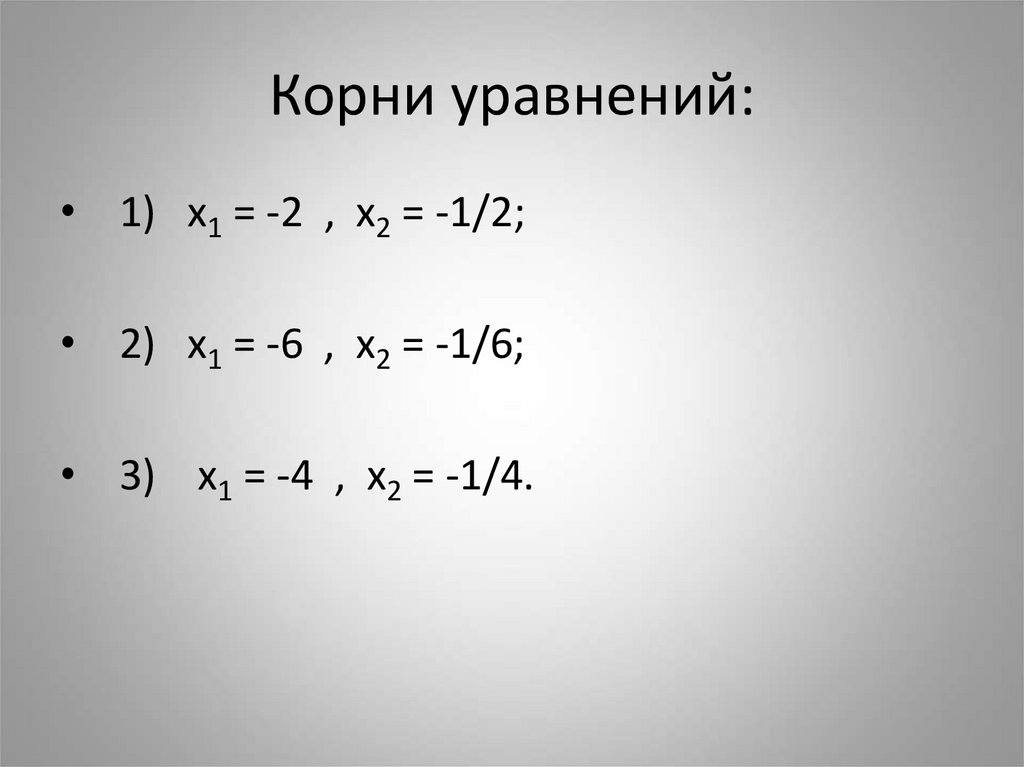





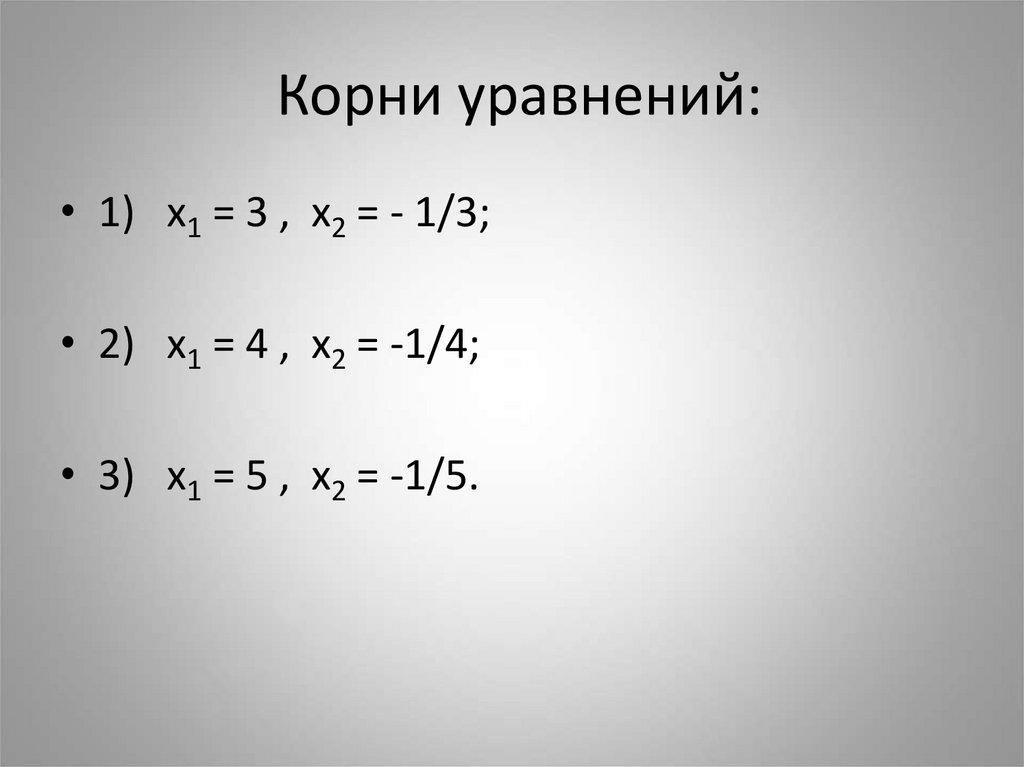

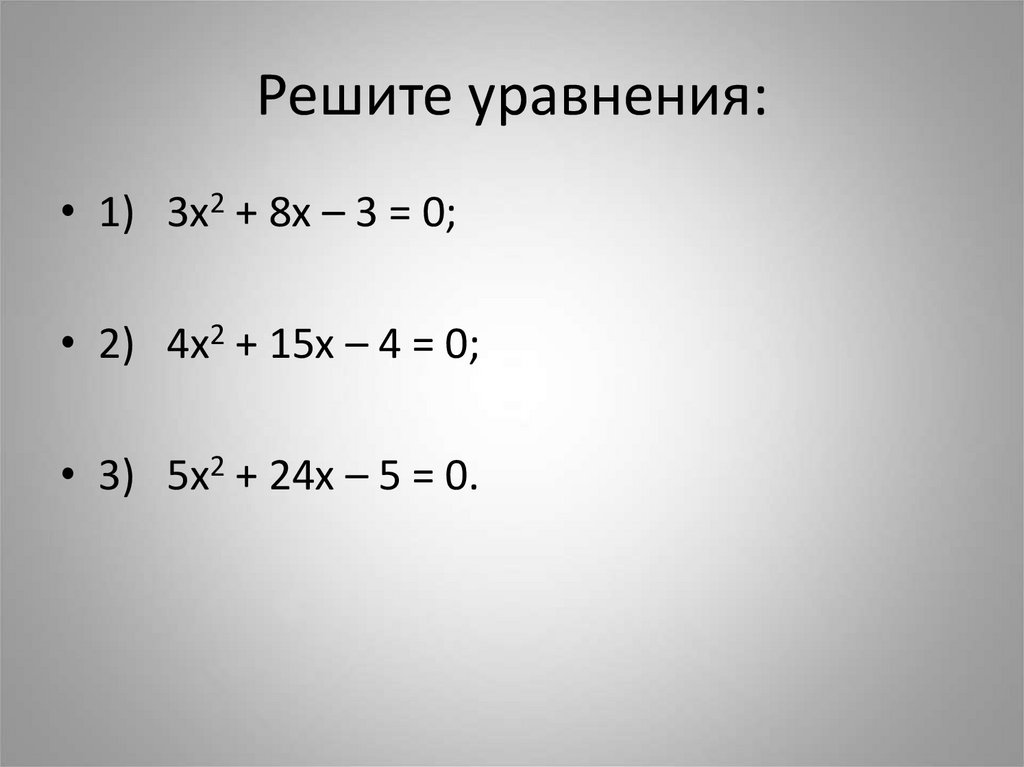




 Математика
Математика








