Квадратные уравнения. Квадратные уравнения в древние времена

1. Квадратные уравнения

Квадратные уравнения - это
фундамент, на котором покоится
величественное здание алгебры.
8 класс

2. Квадратные уравнения в древние времена

• Необходимость решать уравнения второй степени ёщё в
древности была вызвана потребностью решать задачи,
связанные с нахождением площадей земельных участков а
также с развитием астрономии и самой математики.
Квадратные уравнения умели решать около 2000 лет до нашей
веры вавилоняне.
• В древней Греции они решались с помощью геометрических
построений. Евклид и другие ученые решали только
практические задачи. Например, найти сторону квадрата по
его площади.. Методы, которые не связывались с геометрией,
впервые приводит Диофант Александрийский в III в. н.э. В
своей книге «Арифметика»дает решение неполных
квадратных уравнений.

3. Квадратные уравнения в Индии

Задачи на квадратные уравнения встречаются уже в 499г. математиком
и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта
(VII век), изложил общее правило решения квадратных уравнений
В Древней Индии были распространены публичные соревнования в
решении трудных задач. В одной из старинных индийских книг
говорится по поводу таких соревнований следующее: "Как солнце
блеском своим затмевает звезды, так ученый человек затмит славу
другого в народных собраниях, предлагая и решая алгебраические
задачи.

4.

Квадратные уравнения в
Европе 13-17 век
Квадратные уравнения известны человечеству не одно
тысячелетие, формулы решения квадратных уравнений в Европе
были впервые изложены в 1202 г. итальянским математиком
Леонардом Фибоначчи.
Общее правило решения квадратных уравнений было
сформировано немецким математиком М. Штифелем (1487 - 1567).
Выводом формулы общего решения квадратных уравнений
занимался Виет. Он же и вывел формулы зависимости корней
уравнения от коэффициентов в 1591 году. После трудов
нидерландского математика А. Жирара (1595 - 1632), а также
Декарта и Ньютона способ решения квадратных уравнений
приобрел современный вид.

5. Виды квадатных уравнений:

Квадратным уравнением называется уравнение вида ax2+bx+c=0,
где x - переменная, a, b, c - некоторые числа, причем a≠0.
Квадратное уравнение называется неполнным если хотя бы один из
коэффициентов b, c равен о.
Квадратное уравнение называется приведенным если коэффициент
a=1
При каком значении параметра Р уравнение будет
неполным квадратным?
3х² + (р – 59)х + 62 – 2р = 0

6. Решение неполных квадратных уравнений

х(ах + в)=0
х=о; ах+в=0
х = -в/а
ах²+с=0
ах² = -с
х² = -с/а
х1= -√(с/а) х2=√(с/а)
Если - с/а <0, то уравнение не имеет
корней.
Реши уравнения
3х² - 75 = 0
х² + 9 = 0
5х² - 2х = 0

7. Алгоритм решения квадратного уравнения по формуле

Найти число, называемое
дискриминантом квадратного
уравнения и равное D=b2-4ac.
- если D<0, то данное квадратное уравнение не
имеет корней;
- если D=0, то данное квадратное уравнение имеет
единственный корень, который равен :
если D>0, то данное квадратное уравнение имеет два
корня, которые равны :

8.

Проверь свои знания?
1 вариант:
Один из корней уравнения 2х² - 3х – 2 = 0 является
корнем уравнения 2х² - 5х + 2 = 0. На сколько этот
корень меньше 5 ?
2 Вариант:
Х1 и Х2 корни уравнения -х² + 7х + 8 = 0, найди значение
выражения (х1)² - 2х1х2 + (х2)²

9. Решение квадратных уравнений с параметрами

При каком значении параметра
Р уравнение имеет один корень?
1 вариант:
х² + 3рх + р = 0
2 вариант:
х² - 3х + 2 =0
х-р

10.

Реши уравнение:
(3х + 4)² + (5х – 1)² = 38 + х

11.

Франсуа Виет

12.

Теорема Виета
Если приведенное квадратное уравнение x2+px+q=0
имеет действительные корни, то их сумма равна -p,
а произведение равно q, то есть
x1 + x2 = -p ,
x 1 x2 = q
х² + 5х +а = 0
(сумма корней приведенного квадратного уравнения равна
второму коэффициенту, взятому с противоположным
знаком, а произведение корней равно свободному члену).

13.

Проверь себя:
Один из корней уравнения равен
-2. Найдите коэффициент а
и второй корень:
х² + 5х +а = 0
х² + ах + 20 = 0

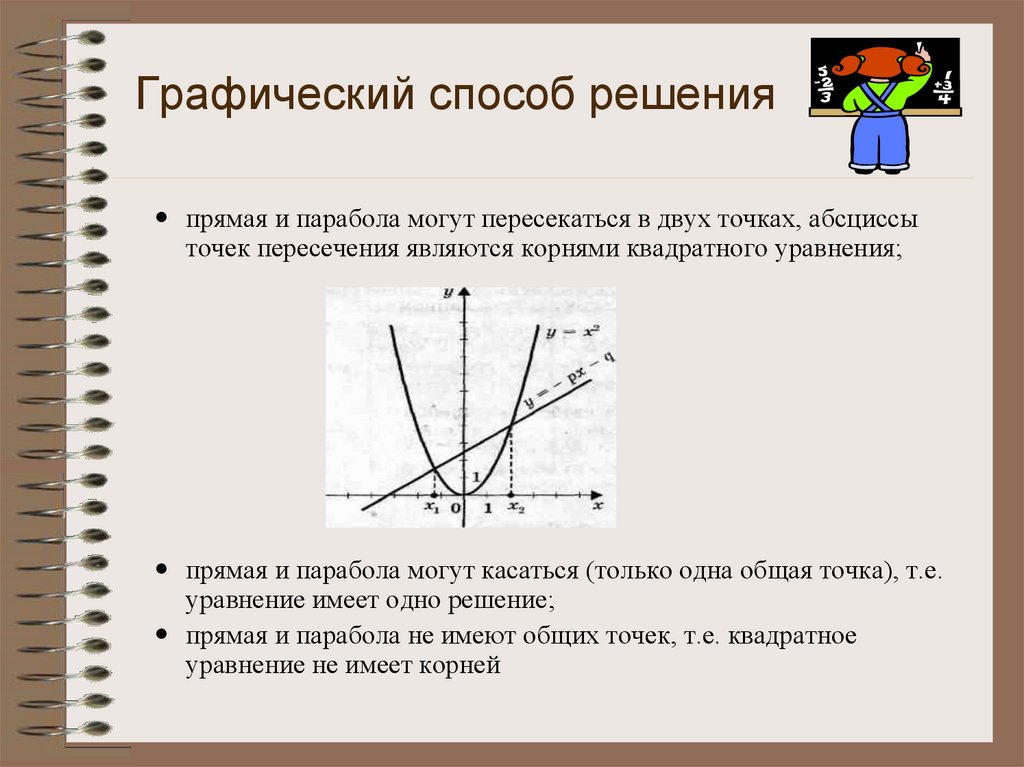
14. Графический способ решения

прямая и парабола могут пересекаться в двух точках, абсциссы
точек пересечения являются корнями квадратного уравнения;
прямая и парабола могут касаться (только одна общая точка), т.е.
уравнение имеет одно решение;
прямая и парабола не имеют общих точек, т.е. квадратное
уравнение не имеет корней

15.

Проверь свои знания?
Решить уравнение графически:
Х² + 4х +3 = 0

16. Спасибо за внимание !