Определение квадратного уравнения. Неполные квадратные уравнения

1.

ТЕМА
УРОКА:
Определение
квадратного уравнения.
Неполные квадратные
уравнения

2. Девиз урока: «Дорогу осилит идущий, а математику - мыслящий!»

Принцип урока:
Я слышу, я вижу, я делаю.

3. Неполные квадратные уравнения

Цель урока:
Научиться классифицировать
квадратные уравнения и решать неполные
квадратные уравнения различными способами.

4.

Уравнение
Уравнением называется равенство,
содержащее переменную, значение которой
надо найти.
• Корень уравнения – значение переменной,
при котором получается верное равенство.
Решить уравнение — найти все его корни
(или убедиться, что их нет).
а) х - 5 = 0;
б) 2у- 4 = 0;
в) n(n + 5) = 0;
г) m² = 16;
д) c² – 9 = 0 ;
е) 5х = 0.

5.

Определение квадратного
уравнения
Квадратным уравнением называется
уравнение вида ах²+вх+с=0, где х – переменная;
а, в, с – любые действительные числа,
причем а≠0.
Числа а, в, с – коэффициенты квадратного уравнения.
а – первый или старший коэффициент,
в – второй коэффициент или коэффициент при х,
с – свободный член.

6.

Является ли квадратным
уравнение?
• а) 2х² + 7х – 3 = 0;
д) х² – 6х + 1 = 0;
• б) 5х – 7 = 0;
е) 7х + 5х = 0;
• в) –х² – 5х – 1 = 0;
ж) 4х² + 1 = 0;
• г) 3х + 4 = 0;
з) х² – 36 = 0.

7.

Приведите уравнение
к виду ах² + bх + с = 0
• а) –х + 2х² – 4 = 0;
г) 18 – 7х + х² = 0;
• б) 2х² – 3х = – 1;
д) 3 – х² + х = 0.
• в) х + 8 – 9х² = 0;

8.

Определите коэффициенты
квадратного уравнения:
• 6х2 + 4х + 2 = 0
а=
b=
c=
• -2х2 + х - 1 = 0
а=
b=
c=
• 8х2 – 7х = 0
а=
b=
c=
• х2 – 0,7 = 0
а=
b=
c=

9.

Приведённое и неприведённое
квадратное уравнение.
• Квадратное уравнение называют приведённым,
если его старший коэффициент =1.
х² – 6х + 1 = 0
• Квадратное уравнение называют неприведённым,
если старший коэффициент отличен от 1.
2х² + 10х – 6 = 0
• Чтобы квадратное уравнение стало приведённым
надо коэффициенты квадратного уравнения
разделить на старший коэффициент.

10.

Преобразуйте квадратное
уравнение в приведённое:
• а) –х² + 2х – 5 = 0;
г) 3х² + 9х –21 = 0;
• б) х² + 3х – 1 = 0;
0;
д) 5х² + 10х + 20 =
• в) 2х² – 4х = 0;
е) 8х²+24 = 0.

11.

Здоровьесберегающие технологии
Вперёд четыре шага,
Назад четыре шага.
Кружится, кружится
Наш хоровод.
Ручками похлопаем,
Ножками потопаем,
Плечиком подвигаем,
А потом попрыгаем.

12.

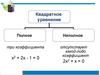
Квадратное уравнение
Полное квадратное
уравнение — это
уравнение, в котором
присутствуют все три
слагаемых; иными словами, это
уравнение, у которого
коэффициенты в и с отличны от
нуля.
Неполное квадратное
уравнение — это
уравнение, в котором
присутствуют не все три
слагаемых; иными словами, это
уравнение, у которого хотя бы
один из коэффициентов в, с
равен нулю.

13.

Виды неполных
квадратных уравнений
• Если b = 0, то уравнение имеет вид
ах2 + c=0
• Если с = 0, то уравнение имеет вид
ах2 + bx =0
• Если b = 0 и с = 0, то уравнение имеет
вид
ах2 =0

14.

Способы решения
неполных квадратных
уравнений

15.

Примеры неполных
квадратных уравнений
а) –х² +1,2=0
б) -3х² +7х=0
в) 5х² - 2=0
г) 7х² =0
д) х²+4х =0
,где а= , в= , с= ;
а= , в= , с= ;
а= , в= , с= ;
а= , в= , с= ;
а= , в= , с= .

16.

Примеры решения неполных
квадратных уравнений
• ах2 + c=0
Пример №1
-3х2 +75=0
-3х2 = -75
х2 = -75:(-3)
х2 =25
х1 = 5 х2 = -5
Ответ: х1 = 5 х2 = 5
Пример №2
4х2 +8=0
4х2 = -8
х2 = -8:4
х2 = -2
Ответ: корней нет
• ах2 + bx =0
Пример №1
4х2 +12х=0
х(4х + 12) = 0
х = 0 или 4х + 12 = 0
х = -12:4
х = -3
Ответ: х1 = 0 х2 = -3
• ах2 =0
Пример №1
0,2х2 =0
х2 =0:0,2
х2 =0
х =0
Ответ: х = 0

17.

Закрепление
• – Какое уравнение называется квадратным?
• – Может ли коэффициент а в квадратном уравнении
быть равным нулю?
• – Является ли уравнение 3х² – 7 = 0 квадратным? Назовите
коэффициенты этого уравнения.
• – Какое квадратное уравнение называется неполным?
• – Какое квадратное уравнение называется приведённым?
• – Как преобразовать неприведённое квадратное уравнение
в приведённое?

18. Какие из данных уравнений являются квадратными? а) 3х+х2=0; д) х2+8х+1=0; б) 2х-5=4; е) х2-9х=0; в) -3х2+2х-5=0; ж) 5х2=0; г)

Какие из данных уравнений являются
квадратными?
а) 3х+х2=0;
б) 2х-5=4;
в) -3х2+2х-5=0;
г) 2х2-7=0;
д) х2+8х+1=0;
е) х2-9х=0;
ж) 5х2=0;
з) х+2=0;
Какие из этих уравнений являются неполными
квадратными?
Укажите коэффициенты уравнений в пунктах
а), в), д).

19. Исторические сведения.

А когда люди научились решать квадратные уравнения?
Древние греки - Евклид и другие ученые – квадратные уравнения
решали геометрическим путем. Задачи, которые они решали, имели
практическую направленность. Например, найти сторону квадрата по его
площади, или радиус круга тоже по площади.
В Древнем Вавилоне образованные люди (жрецы и чиновники)
умели решать задачи на определение длины и ширины прямоугольника
по площади и периметру.
Багдад 9 век. Математик аль-Хорезми предлагает правило решения
квадратных уравнений в точности соответствующее действиям по
нашим формулам, но изложено риторически.
Выдающийся французский математик 16 века Франсуа Виет ввел для
коэффициентов буквы и получил равенство, связывающее корни
уравнения.
После трудов нидерландского математика Жирара, а также
Декарта и Ньютона способ решения квадратных уравнений
принял современный вид.

20. Домашнее задание: п. 28, № 638, 641, 647

21. « Пусть каждый день и каждый час Вам новое добудет. Пусть добрым будет ум у вас, а сердце умным будет». С. Маршак

« Пусть каждый день и каждый час
Вам новое добудет.
Пусть добрым будет ум у вас,
а сердце умным будет».
С. Маршак