Квадратичная функция

1. Квадратичная функция

Презентация к уроку – практикуму по
алгебре, 9 класс
Автор: Морозова Надежда Павловна
учитель математики
МБОУ Пеновская СОШ
имени Е.И. Чайкиной
п.Пено

2. Цели урока

познавательные: обобщение и
систематизация построения графика
квадратичной функции по схеме
коммуникативные: уметь оформлять свои
мысли в устной и письменной речи с учётом
речевых ситуаций
регулятивные: развивать умение видеть
математическую задачу в контексте
проблемной ситуации
личностные: адекватно оценивать
результаты своей учебной деятельности

3. Ход урока

Устная работа
Фронтальный опрос
Выполнение заданий
Итог урока

4.

Выберите правильное
утверждение
Чтобы построить график квадратичной
функции у=ах2+вх+с, необходимо
вычислить координаты вершины
параболы по формулам
n=в/2а, n=-D/2а
Чтобы построить график квадратичной
функции у=ах2+вх+с, необходимо
вычислить координаты вершины
параболы по формулам m=-в/2а,
n=-D/4а или n=y(m)

5.

Выберите правильное
утверждение
Провести через любую точку параболы
прямую, параллельную оси абцисс ось симметрии параболы
Провести через вершину параболы
прямую, параллельную оси ординат ось симметрии параболы

6.

Выберите правильное
утверждение
Найти нули функции, если они есть,
и построить на оси ординат
соответствующие точки параболы
Найти нули функции, если они есть,
и построить на оси абцисс
соответствующие точки параболы

7.

Выберите правильное
утверждение
Построить две какие-нибудь точки
параболы, симметричные относительно её
оси. Для этого необходимо взять любые
две точки на оси Ох . Вычислить
соответствующие значения функции(эти
значения одинаковые).
Построить две какие-нибудь точки
параболы, симметричные относительно её
оси. Для этого необходимо взять две точки
на оси Ох симметричные относительно m.
Вычислить соответствующие значения
функции(эти значения одинаковые).

8. Определите правильный порядок утверждений

1.
2.
3.
4.
5.
Провести через вершину параболы прямую,
параллельную оси ординат - ось симметрии
параболы
Провести через построенные точки параболу
Найти нули функции, если они есть, и построить
на оси абцисс соответствующие точки параболы
Чтобы построить график квадратичной функции
у=ах2+вх+с, необходимо вычислить координаты
вершины параболы по формулам m=-в/2а n=D/4a
Построить две какие-нибудь точки параболы,
симметричные относительно её оси. Для этого
необходимо взять две точки на оси Ох
симметричные относительно m. Вычислить
соответствующие значения функции(эти
значения одинаковые)

9. Правильный ответ

1.
2.
3.
4.
5.
Чтобы построить график квадратичной функции
у=ах2+вх+с, необходимо вычислить координаты
вершины параболы по формулам m=-в/2а, n=-D/4a
Провести через вершину параболы прямую,
параллельную оси ординат - ось симметрии
параболы
Найти нули функции, если они есть, и построить на
оси абцисс соответствующие точки параболы
Построить две какие-нибудь точки параболы,
симметричные относительно её оси. Для этого
необходимо взять две точки на оси Ох
симметричные относительно m. Вычислить
соответствующие значения функции(эти значения
одинаковые)
Провести через построенные точки параболу

10.

11.

Подумайте
В каких случаях
квадратичная функция
имеет наименьшее
значение?
При а больше нуля

12.

13.

Подумайте
Если
а меньше нуля, то
какое значение имеет
функция?
Наибольшее

14.

15.

Подумайте
Бывают ли такие случаи, когда
график функции не пересекает
ось абцисс?
Бывают. Если при вычислении
нулей функции получается ,что
дискриминант не имеет
действительных корней

16.

17. Задача №1

Известны координаты вершины
параболы. Определите
коэффициент а уравнения
параболы.
у=ах2+6х+13
у=ах2-6х+1
(3;4)
(1;2)
а=-1
а=3

18. Задача №2

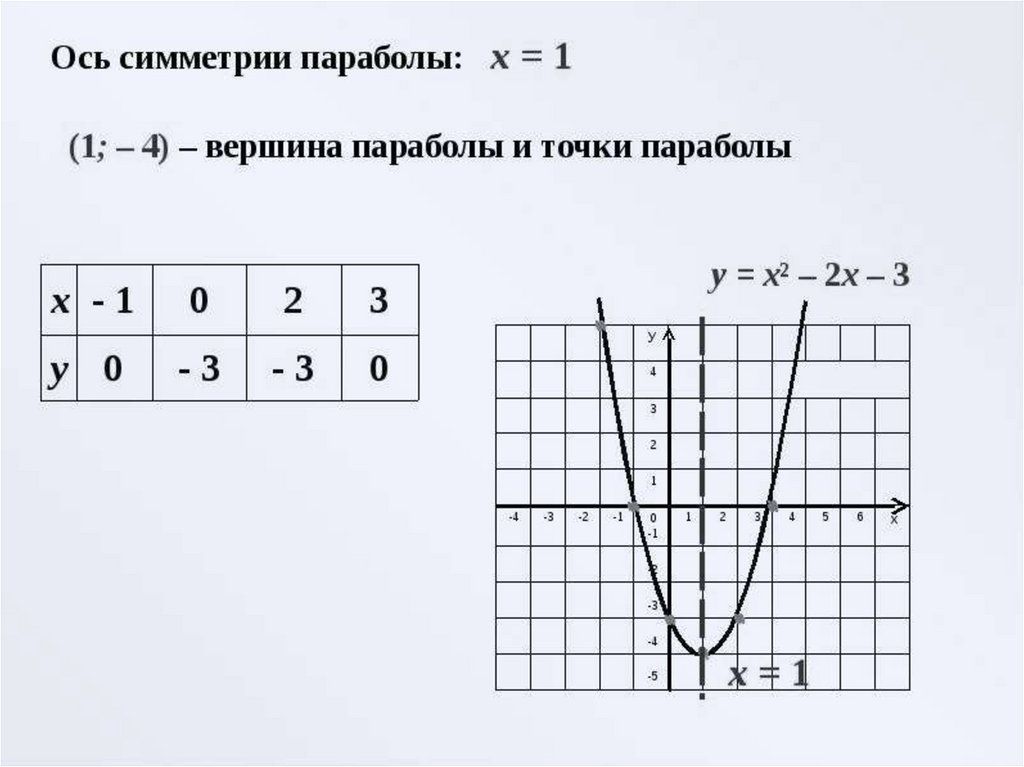
Найдите нули функции:
у=х2+4х-5
у=х2-5х+6
х1=-5; х2=1.
х1=2; х2=3

19. Итог урока

Построение графика квадратичной
функции можно выполнить по схеме
Необходимо уметь находить
координаты вершины параболы
Нули функции
Пару дополнительных точек,
симметричных относительно оси
симметрии параболы

20. Падение баскетбольного мяча

21. Параболический фонтан

22. Библиотека с крышей в форме параболы в норвегии

23. Литература

Алгебра. 9 класс: учеб.для
общеобразовательных учреждений /
авторы:Ю.Н. Макарычев, Н.Г.
Миндюк, К.И.Нешков, С.Б. Суворова/
под ред. С.А. Теляковского.М.:Просвещение, 2018г.