Элементы комбинаторики, статистики и теории вероятностей

1. Элементы комбинаторики, статистики и теории вероятностей

Разработано:
Учитель математики
МБОУ СОШ №8
Исакова Марина Викторовна
г. Бердск

2.

3.

Стохастическим называют опыт, если заранее
нельзя предугадать его результаты. Результаты
(исходы) такого опыта называются событиями.
Пример: выбрасывается игральный кубик (опыт);
выпадает двойка (событие).
Событие, которое обязательно произойдет в
результате испытания, называется достоверным, а
которое не может произойти, - невозможным.
Пример: В мешке лежат три картофелины.
Опыт – изъятие овоща из мешка.
Достоверное событие – изъятие картофелины.
Невозможное событие – изъятие кабачка.

4.

Равновозможными называют события, если в
результате опыта ни одно из них не имеет большую
возможность появления, чем другие.
Примеры:
1) Опыт - выбрасывается монета.
Выпадение орла и выпадение решки –равновозможные
события.
2) В урне лежат три шара. Два белых и синий. Опыт –
извлечение шара.
События – извлекли синий шар и извлекли белый шар неравновозможны. Появление белого шара имеет больше
шансов.

5.

Несовместимыми (несовместными) называют
события, если наступление одного из них
исключает наступление других.
Пример:
1) В результате одного выбрасывания выпадает орел
(событие А) или решка (событие В). События А и В несовместны.
2) В результате двух выбрасываний выпадает орел
(событие А) или решка (событие В). События А и В совместны. Выпадение орла в первый раз не
исключает выпадение решки во второй.

6.

Полной группой событий называется
множество всех событий рассматриваемого
опыта, одно из которых обязательно произойдет,
а любые два других несовместны.
События образующие полную группу называют
элементарными.
Пример:
1) Опыт – один раз выбрасывается монета.
Элементарные события: выпадение орла и выпадение
решки образуют полную группу.

7.

Вероятностью события «А» называют отношение
числа благоприятствующих этому событию исходов к
общему числу всех равновозможных несовместных
элементарных исходов, образующих полную группу:
где m – число элементарных исходов,
благоприятствующих А;
n – число всех возможных элементарных исходов
испытания.

8. В чемпионате по гимнастике участвуют 50 спортсменок: 24 из США, 13 из Мексики, остальные — из Канады. Порядок, в котором

В чемпионате по гимнастике участвуют 50 спортсменок:
24 из США, 13 из Мексики, остальные — из Канады.
Порядок, в котором выступают гимнастки, определяется
жребием. Найдите вероятность того, что спортсменка,
выступающая
первой,
окажется
из
Канады.
m – число элементарных исходов, благоприятствующих А,
т.е. количество благоприятных событий, соответствует
количеству гимнасток из Канады - 13 чел.
n – число всех возможных элементарных исходов
испытания, т.е. количество всех событий группы
соответствует общему количеству гимнасток – 50 чел.
Тогда вероятность
Р(А) = 13: 50 = 13/50= 13/100 =0,26

9. В среднем из 1400 садовых насосов, поступивших в продажу, 14 подтекают. Найдите вероятность того, что один случайно выбранный

для
контроля насос не подтекает.

10. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат

округлите до сотых.
Решение: К-во всех событий группы N=216
1-я кость - 6 вариантов
2-я кость - 6 вариантов
6 6 6 216
3-я кость - 6 вариантов
Благоприятное событие А: в сумме выпало 7
очков.
412
331
313
133
223
232
322
511
151
115
421
124
142
214
241
15
15
Р( А)
0,07
216

11. Статистическая обработка данных

12.

В 9а и 9б классах измерили рост 50 учеников.
Получились следующие результаты:
162, 168, 157, 176, 185, 160, 162, 158, 181, 179, 164, 176, 177, 180,
181, 179, 175, 180, 176, 165, 168, 164, 179, 163, 160, 176, 162, 178,
164, 190, 181, 178, 168, 165, 176, 178, 185, 179, 180, 168, 160, 176,
175, 177, 176, 165, 164, 177, 175, 181.
Данные, собранные в этом списке, являются наиболее
полной информацией о проведенном измерении. К
сожалению, эта информация трудно «читается».

13. Что такое статистика?

Статистика – получение, обработка, анализ и
публикация информации, характеризующей
количественные закономерности жизни в обществе в
неразрывной связи с их количественным
содержанием.
Задачи статистики:
1) обработка информации;
2) получение и хранение информации;
3) выработка различных прогнозов;
4) оценка достоверности прогнозов и т.д.

14. Статистика – дизайн информации

Порядок преобразований первоначально
полученной информации :
сначала данные измерений упорядочивают и
группируют;
затем составляют таблицы распределения данных;
таблицы распределения переводят в графики
распределения;
наконец, получают своего рода паспорт данных
измерения, в котором собрано небольшое количество
основных числовых характеристик полученной
информации.

15.

157, 158, 160, 162, 163, 164, 165, 168, 175, 176, 177, 178, 179,
180, 181,185, 190.
Мы составили ряд данных измерения.
Каждое из этих чисел называют вариантой
измерения.
Варианта измерения – один из результатов этого
измерения.
Не все варианты конкретного измерения находятся
в одинаковом положении. Какие-то встречаются
много раз, какие-то реже, а некоторые встречаются
по одному разу. Это количество называют
кратностью варианты.

16.

Перед дальнейшей обработкой информации
данные измерения группируют.
Составляют сгруппированный ряд данных.
157, 158, 160, 160, 160, 162, 162, 162, 163, 164, 164, 164,
164, 165, 165, 165, 168, 168, 168, 168, 175, 175, 175, 176,
176, 176, 176, 176, 176, 176, 177, 177, 177, 178, 178, 178,
179, 179, 179, 179, 180, 180, 180, 181, 181, 181, 181, 185, 185,
190.
На этом заканчивается первый шаг обработки
информации – ее упорядочивание и
группировка.

17.

Варианта
Кратность
Кратность
Частота
157
158
160
162
163
164
165
168
175
176
177
178
179
180
181
185
190
Сумма
(объем
измерения)
1
1
3
3
1
4
3
4
3
7
3
3
4
3
4
2
1
50
157
158
160
162
163
164
165
Варианта
168 175 176
177
178
179
180
181
185
190
1
1
3
3
1
4
3
4
3
7
3
3
4
3
4
2
1
50
0,02
0,02
0,06
0,06
0,02
0,08
0,06
0,08
0,06
0,14
0,06
0,06
0,08
0,06
0,08
0,04
0,02
1
Сумма
(объем
измерен
ия)

18.

Для удобства счета и построения графиков
частоты переводят в проценты от объема
измерения.
Кратность
Частота
Частота, %
157
158
160
162
163
164
165
1
1
3
3
1
4
3
Варианта
168 175 176
4
3
7
177
178
179
180
181
185
190
3
3
4
3
4
2
1
0,02 0,02 0,06 0,06 0,02 0,08 0,06 0,08 0,06 0,14 0,06 0,06 0,08 0,06 0,08 0,04 0,02
2
2
6
6
2
8
6
8
6
14
6
6
8
6
8
4
2
Сумма
(объем
измерен
ия)
50
1
100

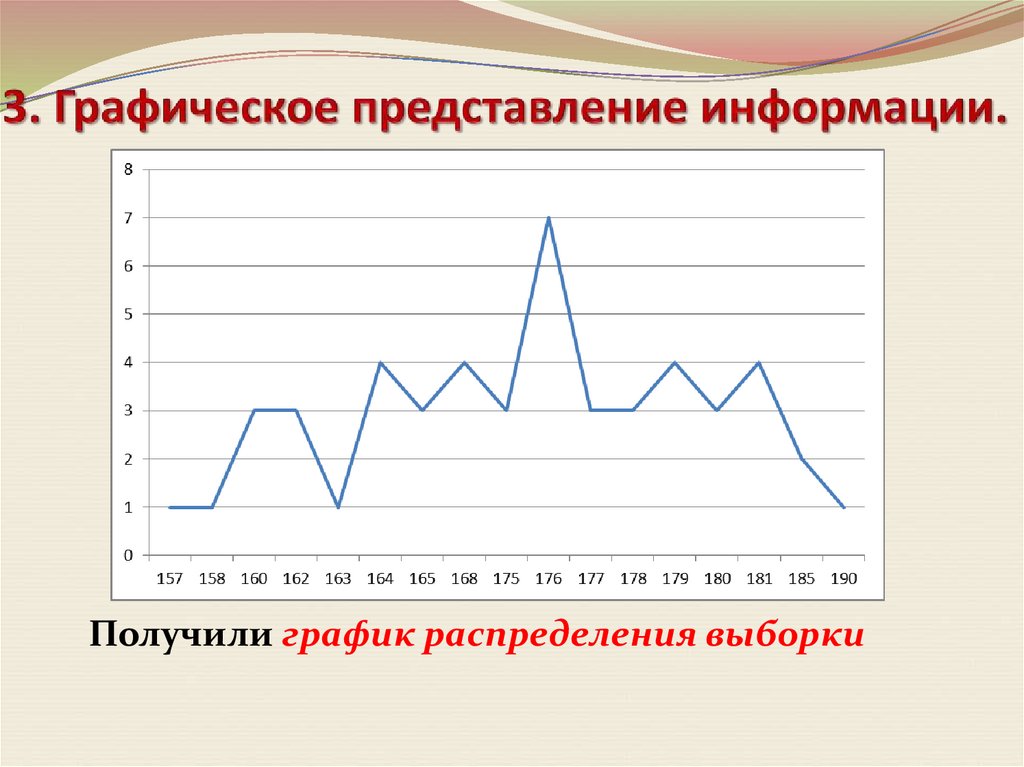
19.

Получили график распределения выборки

20.

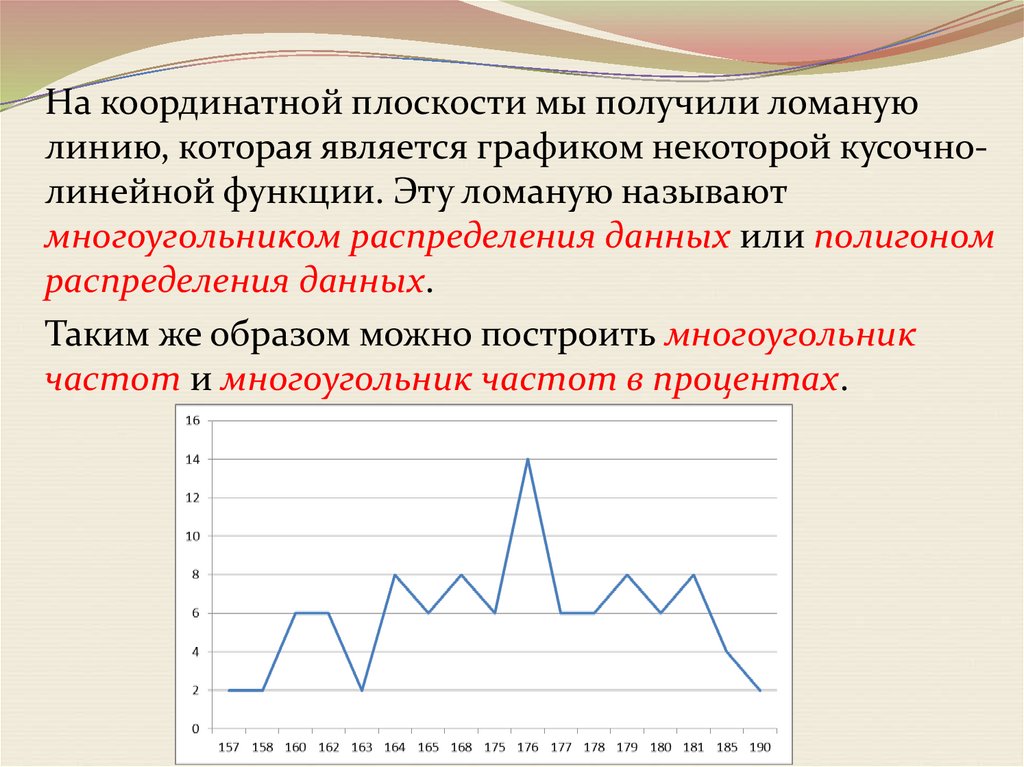
На координатной плоскости мы получили ломаную
линию, которая является графиком некоторой кусочнолинейной функции. Эту ломаную называют
многоугольником распределения данных или полигоном
распределения данных.
Таким же образом можно построить многоугольник
частот и многоугольник частот в процентах.

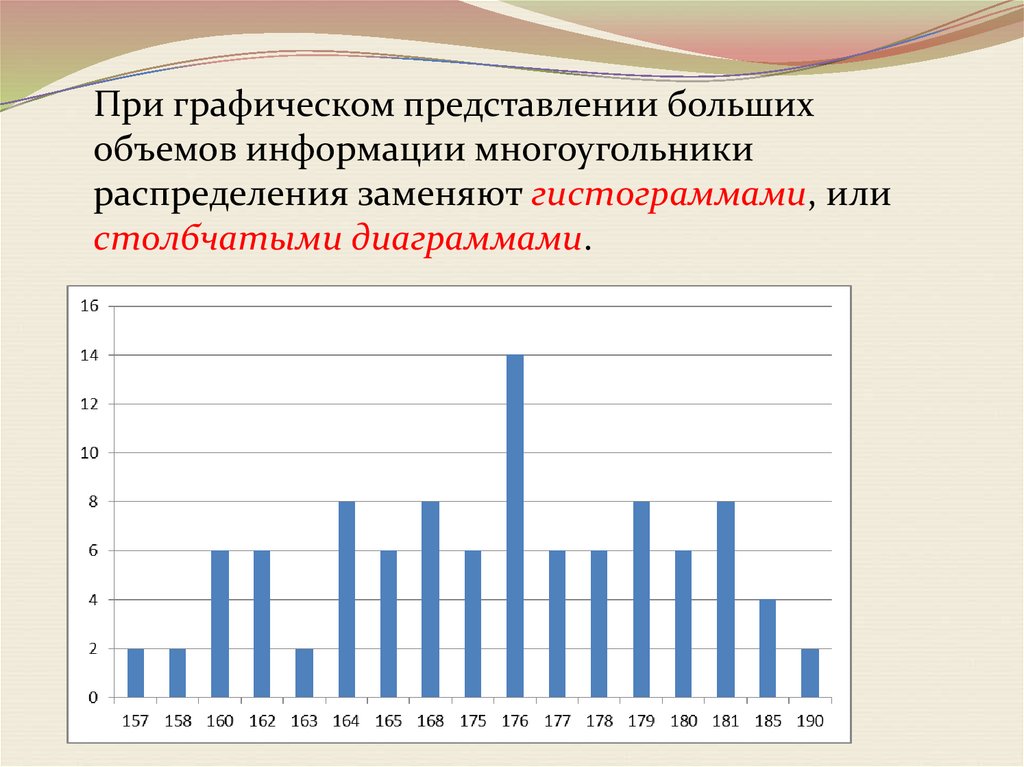
21.

При графическом представлении больших
объемов информации многоугольники
распределения заменяют гистограммами, или
столбчатыми диаграммами.

22.

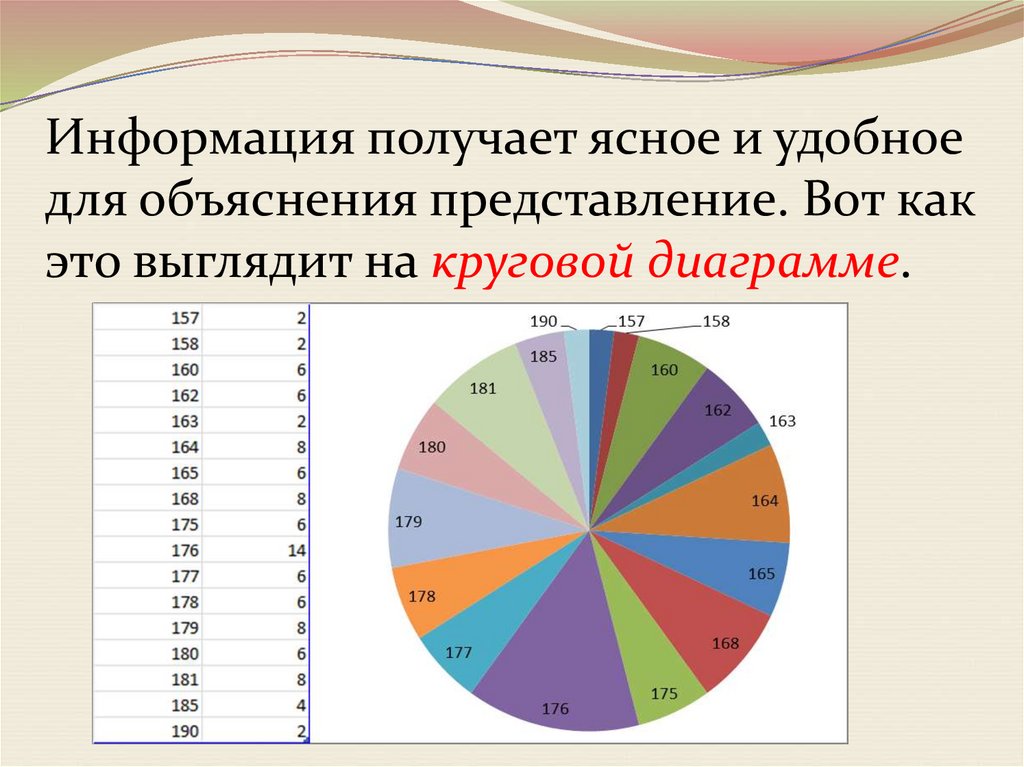
Информация получает ясное и удобное
для объяснения представление. Вот как
это выглядит на круговой диаграмме.

23.

Размах измерения – разность между максимальной и
минимальной вариантами. (190-157=33)
Мода измерения – варианта, которая встречается
чаще других. (176)
Среднее значение (среднее арифметическое):
просуммировать все данные измерения;
полученную сумму разделить на количество
данных.
Медиана – средняя варианта в сгруппированном
ряде. (175). Если средних вариант две, то медиана
равна их полусумме.