Похожие презентации:
Оценка косвенных измерений. МНК
1.
Оценка косвенныхизмерений.
МНК
2.
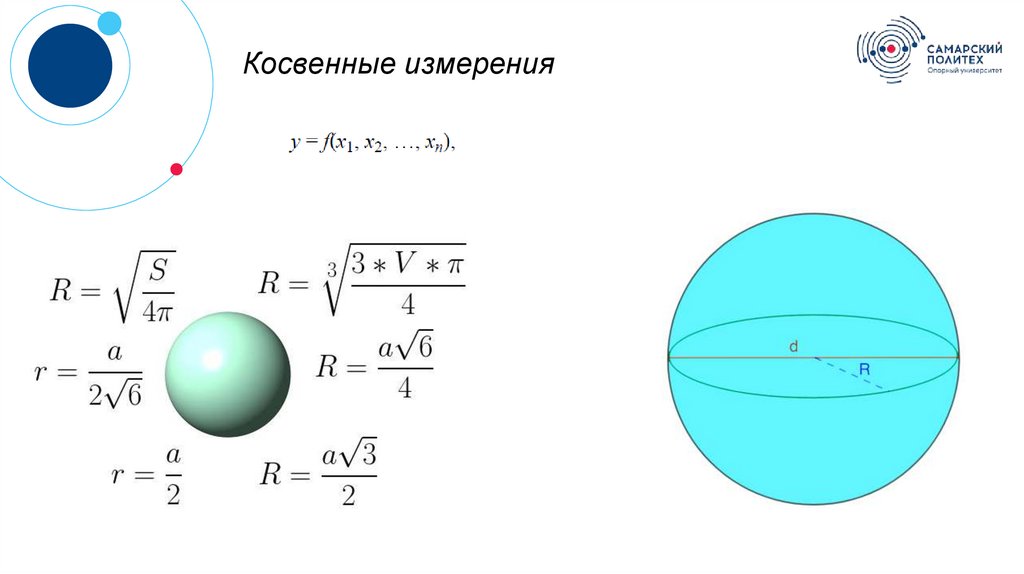
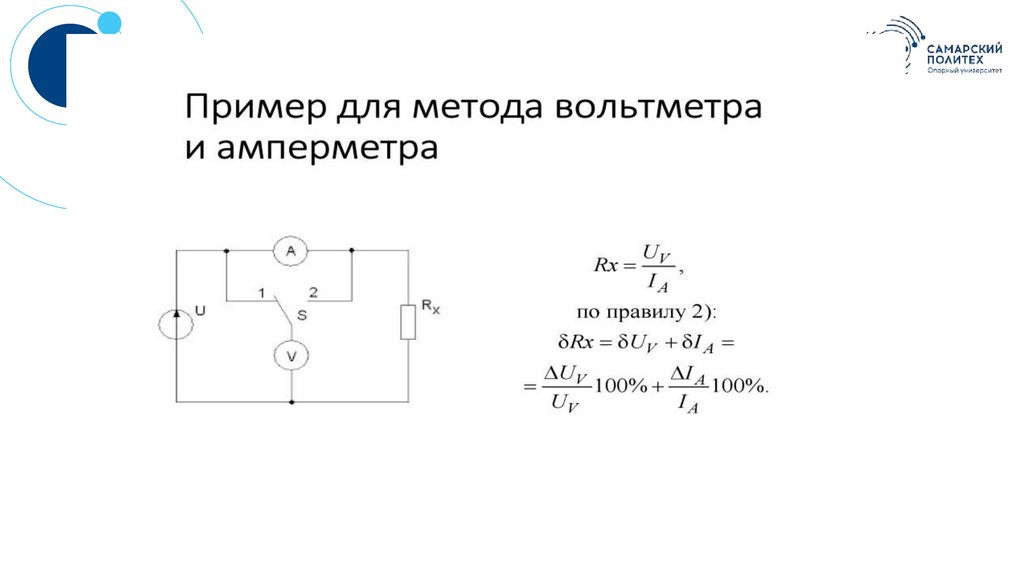
Косвенные измерения3.
?4.
?5.
?6.
?7.
?8.
?9.
?10.
?11.
?12.
?13.
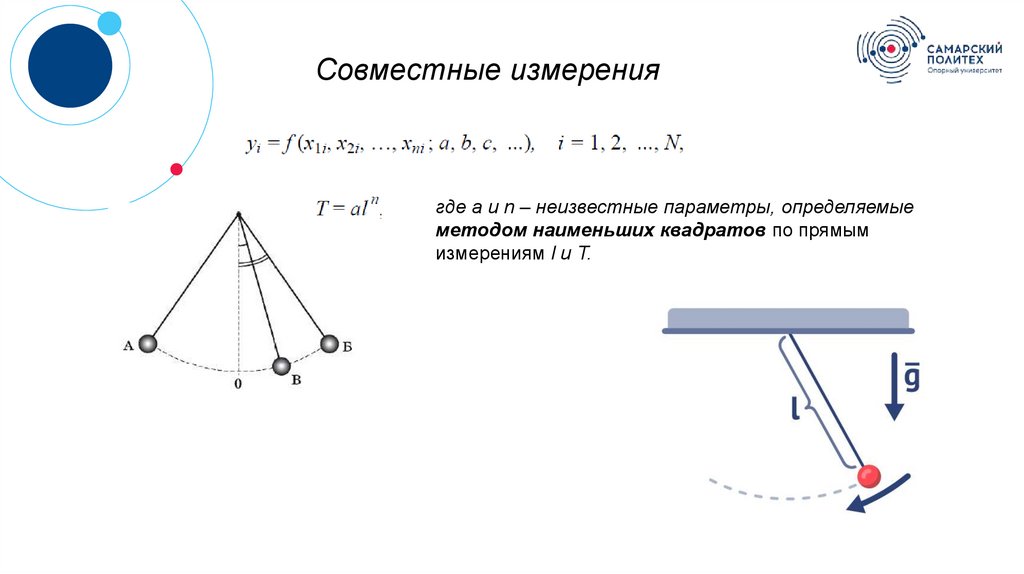
Совместные измерениягде а и n – неизвестные параметры, определяемые
методом наименьших квадратов по прямым
измерениям l и Т.
?
14.
Совокупные измерения?
15.
YYi
εi
Yxi
Yxi a b xi
0
X
16.
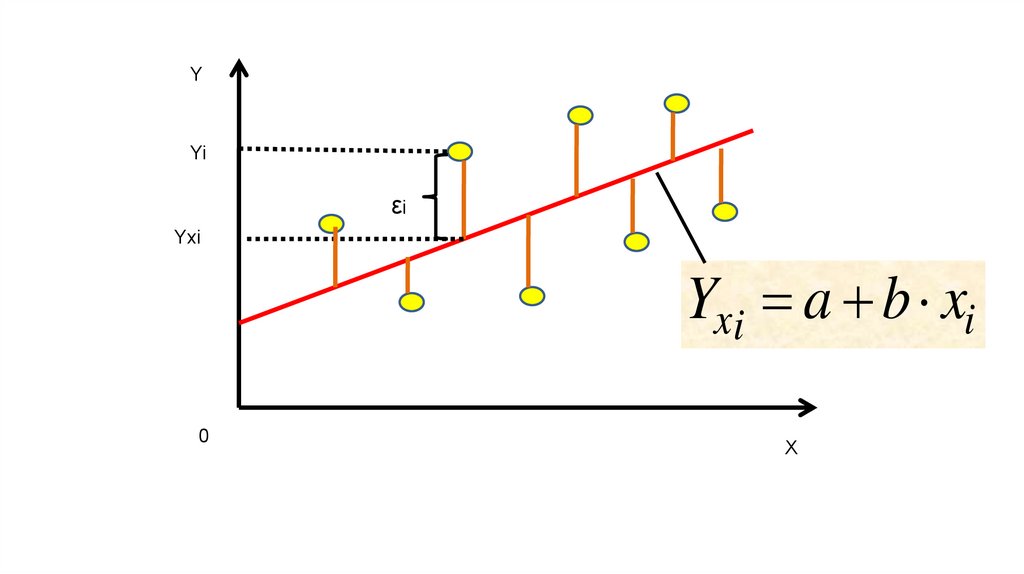
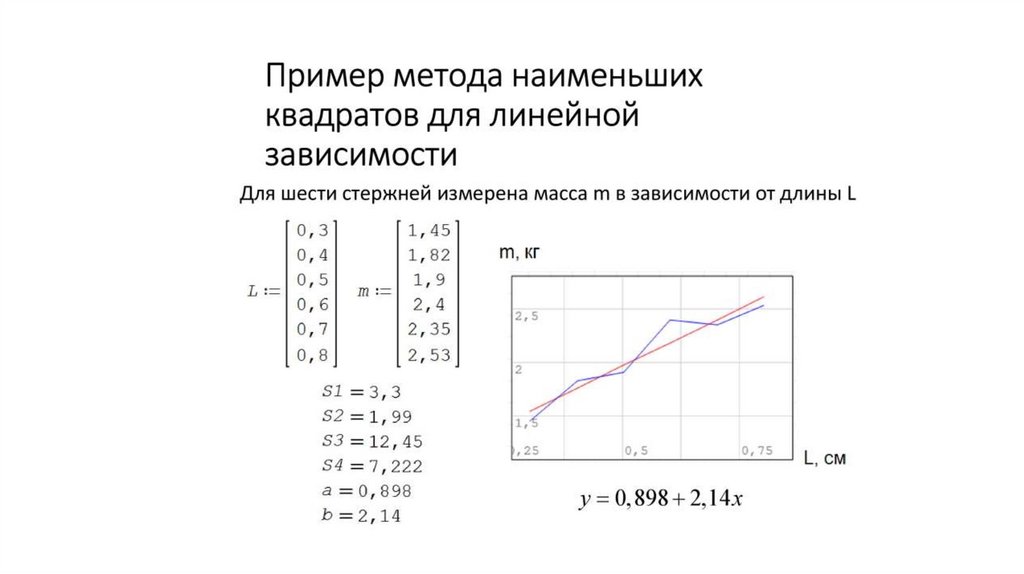
Суть метода наименьших квадратов (МНК) - оценкипараметров таковы, что сумма квадратов отклонений
фактических значений зависимой переменной Y от
расчетных (теоретических) Yx минимальна:
n
( y y ) min
2
i 1
i
xi
17.
Оценка параметров регрессииS ( yi y x i ) ( y a b x ) ;
2
2
dS
2 y 2 n a 2 b x 0;
da
dS
2
2 y x 2 a x 2 b x 0.
db
18.
Оценка параметров регрессии19.
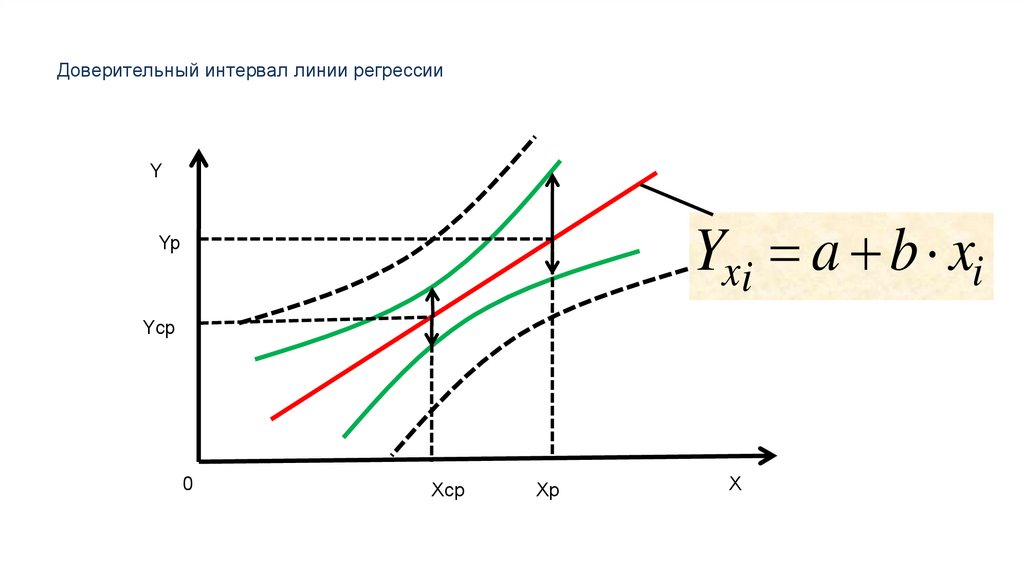
Доверительный интервал линии регрессииY
Yxi a b xi
Yp
Yср
0
Xср
Xp
X
20.
Построение линейной регрессии сводится к оценке ее параметров – a иb
Классический подход к оцениванию параметров основан на методе
наименьших квадратов
Из множества линий на графике выбирается та, для которой минимальна
сумма квадратов расстояний по вертикали между точками наблюдений
и этой линией
21.
Классы нелинейных регрессийЕсли между физическими явлениями существуют нелинейные
соотношения, то они выражаются с помощью нелинейных функций
Регрессии, нелинейные
относительно переменных
• Линейны по параметрам
Регрессии, нелинейные по
оцениваемым параметрам
• Линейны по переменным
22.
Регрессии, нелинейные относительнопеременных
y x a bx сx парабола;
2
b
y x a гипербола;
x
y x a bx сx dx полином;
2
3
23.
Регрессии, нелинейные по оцениваемымпараметрам
y x a x степенная;
b
y x a b показатель ная;
x
yx e
a bx
экспоненци альная
24.
25.
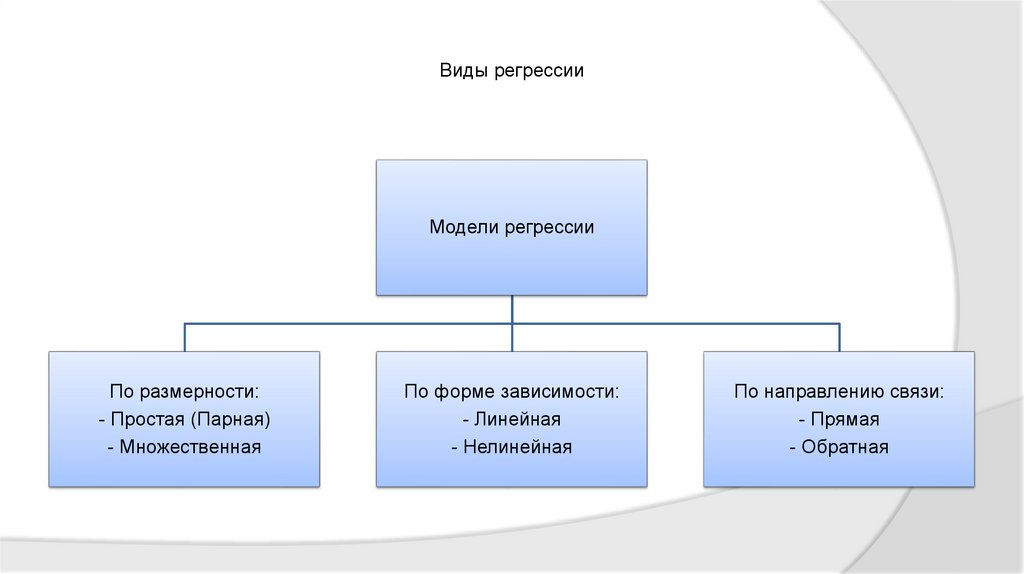
Виды регрессииМодели регрессии
По размерности:
- Простая (Парная)
- Множественная
По форме зависимости:
- Линейная
- Нелинейная
По направлению связи:
- Прямая
- Обратная
26.
Эмпирическое уравнение линейной регрессииYx i a b xi
Yxi - теоретическое (среднее) значение зависимой переменной Y, найденное из уравнения
регрессии
b - эмпирический коэффициент регрессии
а- эмпирический свободный коэффициент
В конкретном случае:
Yi a b xi ei
ei – оценка теоретического случайного отклонения ε
27.
Теоретическая линейная модель парной регрессииYi xi i
α – свободный коэффициент
β - коэффициент регрессии
εi – случайное отклонение (возмущение)
Случайное отклонение включает влияние не учтенных в модели
факторов, случайных ошибок и особенностей измерения. Источники его
присутствия в модели: спецификация модели, выборочный характер
исходных данных, особенности измерения переменных.
28.
Методы выбора типа уравнения регрессииГрафический метод
• Основан на визуальном анализе поля
корреляции
Аналитический метод
• Основан на изучении материальной
природы взаимосвязи
Экспериментальный
метод
• Основан на сравнении величины
остаточной дисперсии, рассчитанной
при разных моделях
29.
YY
0
Yx a b x
X
0
X
Yx a b x c x
2
30.
YY
0
X
0
X
Yx a b / x Yx a b x c x 2 d x3
31.
YY
0
Yx a x
X
b
0
X
Yx a b
x
















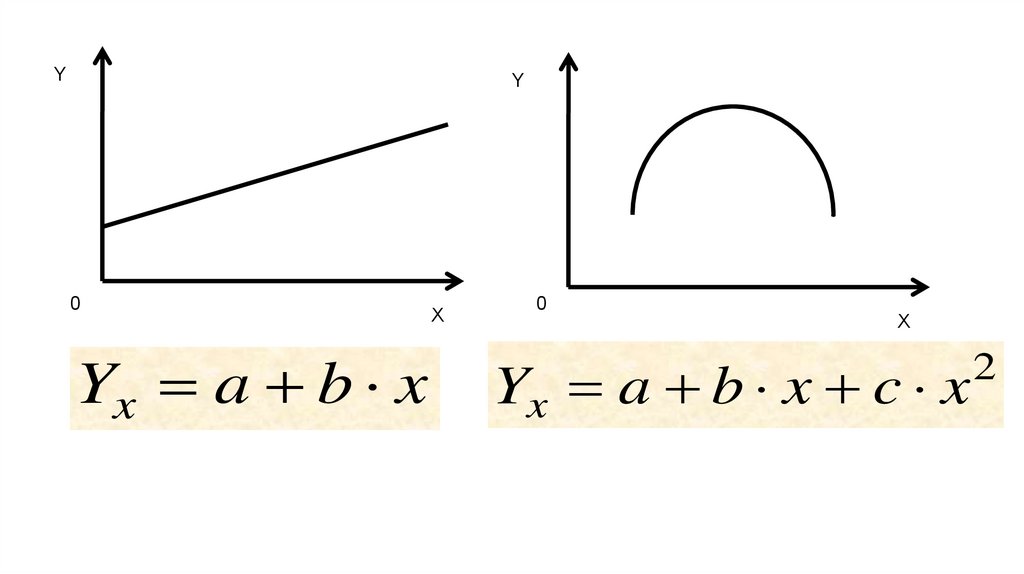
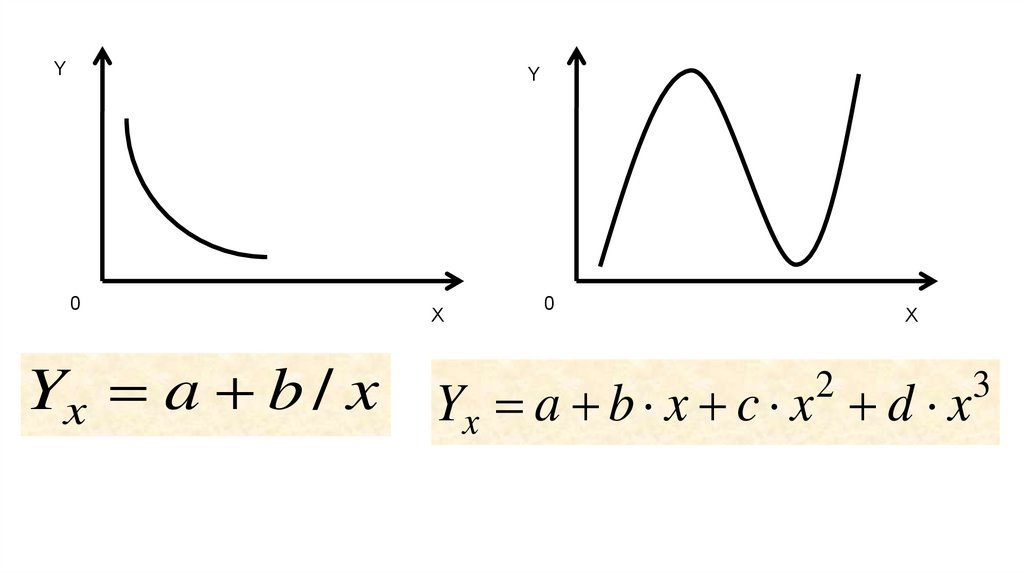
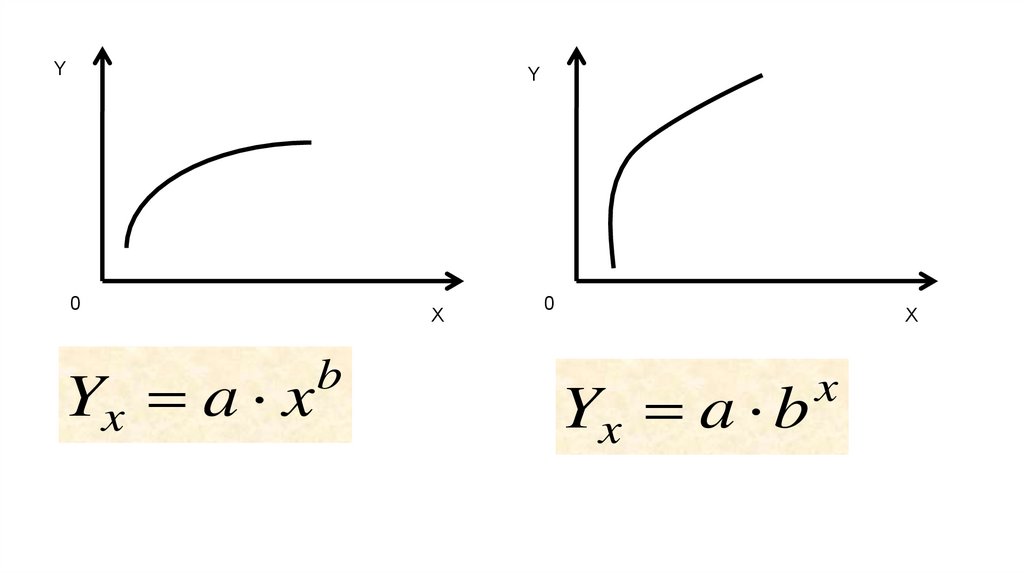

 Математика
Математика








