Похожие презентации:
Эконометрические модели. Модели парной регрессии
1. Лекции №2 - №4 Тема 2: Эконометрические модели. Модели парной регрессии
План:1. Функциональная, статистическая и
корреляционная зависимости.
2. Парная линейная регрессия.
3. Ковариация и корреляция.
4. Проверка значимости выборочного
коэффициента корреляции.
2. 5. Метод наименьших квадратов (МНК). 6. Предпосылки МНК – условия Гаусса – Маркова. 7. Ошибки исследования. 8. Коэффициент
детерминации линейнойрегрессии.
9. Нелинейные модели регрессии и их
линеаризация.
3. 1. Функциональная, статистическая и корреляционная зависимости.
1. Функциональная зависимость - этополное соответствие между зависимой
(результативной) переменной У и
независимыми (факторными)
переменными Xi. Она задается в виде
уравнения
y f xi
4. 2. В экономике такая зависимость бывает редко, потому что на величины влияют случайные факторы , тогда уравнение примет вид в
2. В экономике такая зависимость бываетредко, потому что на величины влияют
случайные факторы i , тогда уравнение
примет вид y f xi i
в этом случае зависимость называется
статистической зависимостью.
Пример.
Урожайности зерновых зависит от ряда
факторов: удобрений, производительности
труда, энерговооруженности сельского
предприятия и т.п.
5. 3. Корреляционная зависимость – это частный случай статистической зависимости, когда изменение средней величины результативной
переменной Упроисходит в зависимости от
математического ожидания изменения
значения факторного признака Х.
Корреляция (от позднелат. correlatio –
соотношение).
6. Для каждого значения Х=х определено условное математическое ожидание М(У/Х=х) величины У по Х, которое равно среднему значению
функции у (х)и называется регрессией величины У по Х.
y ( x) M (Y | X x)
7. Термин «корреляция» впервые применил французский палеонтолог Ж. Кювье, который вывел «закон корреляции частей и органов
животных»(этот закон позволяет восстанавливать по
частям тела облик всего животного).
В статистику термин ввел Френсис
Гальтон (не просто связь –relation, а «как бы
связь»-cо-relation).Формулу для подсчета
коэффициента корреляции разработал его
ученик – математик и биолог – Карл Пирсон
(1857-1936).
8. Примеры корреляционной связи
1. Закон Хика – скорость переработкиинформации пропорциональна логарифму
от числа альтернатив.
2. Корреляция личной пластичности человека
и склонности его к смене социальных
установок.
3. Чем выше личностная тревожность, тем
больше риск заболеть язвой желудка.
4. Чем боязливее особь, тем меньше у нее
шансов занять ведущее положение в
группе.
9. Задачи корреляционного анализа
1. Установление направлениязависимости двух и более переменных
(положительное – прямая связь или
отрицательное – обратная связь).
2. Определение формы зависимости
(линейная, нелинейная).
3. Измерение тесноты связи.
4. Проверка уровня значимости
полученных коэффициентов
корреляции.
10. 2. Парная линейная регрессия
Понятие «регрессия» возникло впсихоанализе (лат. regressio – движение
назад, возвращение к более раннему
состоянию или образу действий).
В математике это понятие впервые
употребил Френсис Гальтон в 1886 г.
как возврат к среднему значению. Он
исследовал зависимость роста сыновей
от роста их отцов (рост очень высоких и
очень низких отцов ближе к среднему
росту детей в регионе).
11. Эконометрический анализ построения модели парной регрессии
По имеющимся данным m наблюденийx1 , x2 ,
, xm
зависимости y от
выбрать эконометрическую модель,
y f xi i
оценить ее параметры и статистически
обосновать, что факторы существенны, и,
что построенная функция наиболее точно
соответствует данным наблюдений.
12. Задачи регрессионного анализа
1. Спецификация модели - определитьвид уравнения регрессии.
2. Параметризация модели - оценить
параметры уравнения.
3. Верификация модели – проверить
адекватность уравнения эмпирическим
данным и улучшить качество
уравнения.
4. Сделать прогноз неизвестных
значений зависимой переменной.
13. 3. Ковариация и корреляция
Co-vary – совместное изменение.Correlatio – соотношение.
Теоретической ковариацией СВ Х и У
называется средняя величина отклонений
этих переменных от своих средних
Cov(X,Y)=M[(X-M(X))•(Y-M(Y))]=
= M(XY)-M(X)•M(Y)
14. Теоретический коэффициент корреляции
Недостатком Cov является еезависимость от размерности СВ Х и У.
Для устранения этого вводится
относительная (безразмерная) величина
– теоретический коэффициент
корреляции
(Х,У) = Cov(Х,У) / σ(Х) • σ(У),
где ρ - читается «ро»
σ (сигма) – среднее квадратическое
отклонение
15. Выборочная ковариация
1 ncov x, y xi x y i y
n i 1
16. Расчетная формула
cov( x, y ) xy x y17. Выборочный коэффициент корреляции
rxyx
xy x y
2
y
x
2
2
y
2
18. Характеристика тесноты линейной связи
Если r = 0, то связь отсутствует.Если 0 < r < 1, то связь положительная,
прямая.
Если -1< r < 0, то связь отрицательная,
обратная.
Если r = +1 или r = -1, то связь строгая
функциональная.
19. 4. Проверка значимости выборочного коэффициента корреляции
Требуется проверить гипотезу Ho оравенстве нулю истинного значения
коэффициента корреляции для
генеральной совокупности. Гипотезы:
Ho: ρ = 0
H1: ρ ≠ 0.
Проверка с помощью
t-критерий Стьюдента с (n-2) степенями
свободы и заданной доверительной
вероятностью
= (0,9; 0,95; 0,98)
20. Если Іtнабл.І < t-критерия Стьюдента, то r незначим и Ho принимается. Если Іtнабд.І > t-критерия Стьюдента, то r значим и Ho
t наблюдаемоеr n 2
1 r
2
Если Іtнабл.І < t-критерия Стьюдента,
то r незначим и Ho принимается.
Если Іtнабд.І > t-критерия Стьюдента,
то r значим и Ho отвергается.
21.
Лекция № 3Слайды 22-62
22. Уравнение линейной регрессии
Для генеральной совокупностизависимость У от Х представим в виде
линейной модели первого порядка
ˆ
Y 0 1 X
Для выборочной совокупности
yˆ b0 b1 x e
23. где e=y-ŷ - оценка ошибки аппроксимации, отклонение, разность между выборочным и расчетным значением. Традиционно уравнение
линейнойрегрессии записывают в виде:
yˆ a b x
24. Экономический смысл параметров
b - коэффициент регрессии,показывает на сколько в среднем
изменится у при изменении х на единицу.
Знак b указывает на направление
связи. Если b > 0, то связь прямая, т.е. с
увеличением х увеличивается у и
наоборот.
Если b < 0, то связь обратная, т.е. с
увеличением х у уменьшается и
наоборот.
а – среднее значение у при х=0.
25. Форма уравнения определяется на основе визуальной (зрительной) оценки. Строится график - корреляционное поле, т.е. оси абсцисс
(ох) откладываютсязначения факторного (независимого)
признака х, а по оси ординат (оу) –
значения результативного признака у.
Соединяя точки графика отрезками
прямой получим эмпирическую линию.
По ее виду судят о наличии зависимости и
о форме линии.
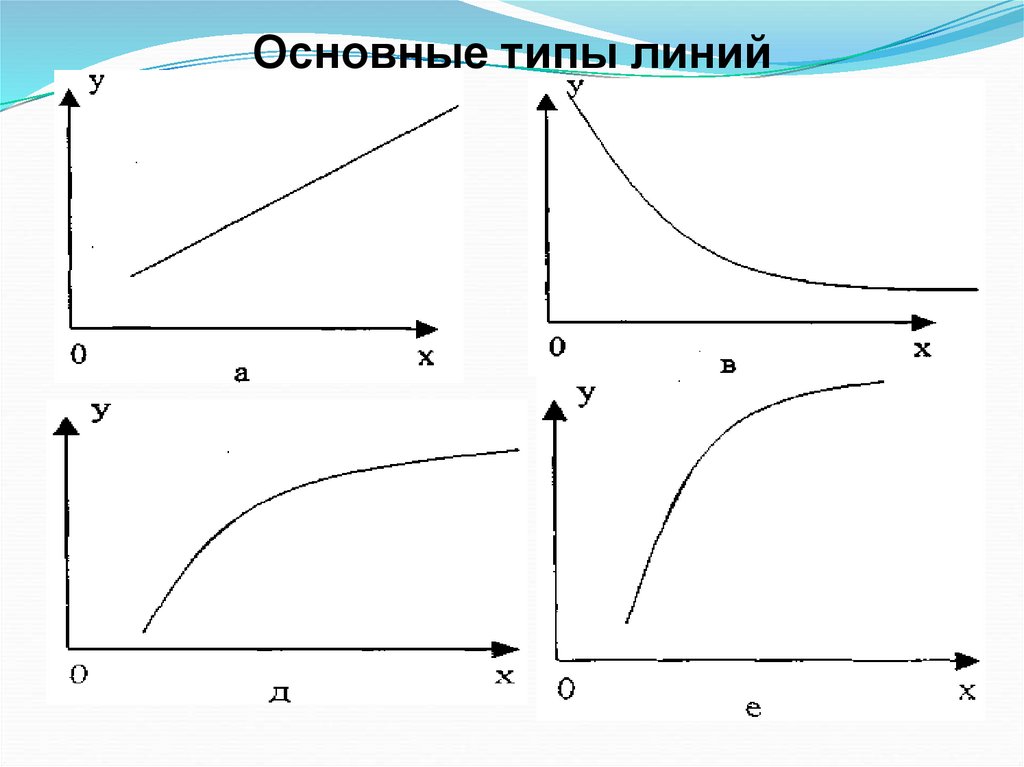
26. Основные типы линий
27. Линейная Гиперболическая Степенная Показательная
Линейнаяyx a b x;
Гиперболическая
yx a b / x;
Степенная
yx a x ;
Показательная
yx a b ;
b
x
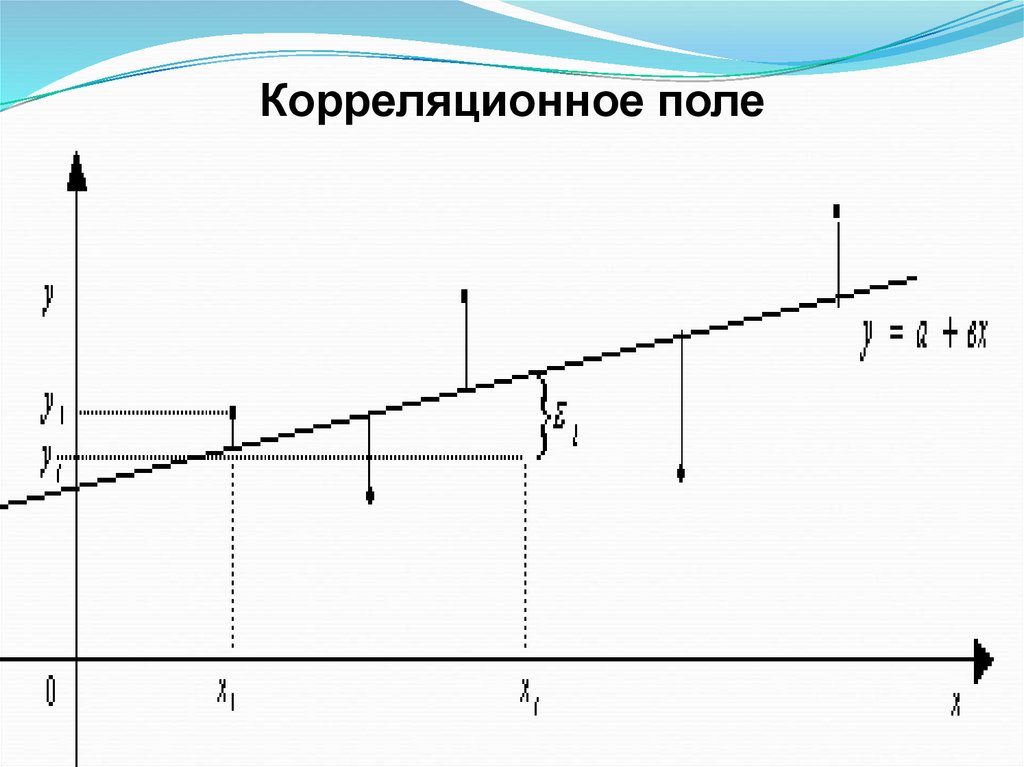
28. Корреляционное поле
29. Пояснения к графику
Случайная выборка значенийх1 , x2 , , xn и y1 , y 2 , , y n
Уравнение регрессии
yˆ a bx
Отклонения
ei yi yˆi
Для каждой точки ( x i , yi ) можно
записать различные виды дисперсий:
30. Виды дисперсий
ДисперсияДисперсия
Дисперсия
yi
ŷi
i
2
1
yi y
n
2
y
2
1
yˆi y
n
2
yˆ
1
i
n
2
2
31. Коэффициент детерминации
2R
2
yˆ
2
y
ˆ
y
y
y
y
0 R 1
2
2
i
2
i
32.
ee
i
2
R 1 1
2
y
y
i
2
2
y
2
33. Коэффициент детерминации оценивает качество (точность) уравнения регрессии, это часть дисперсии (вариации) признака у
объясненная уравнением регрессии.Например: R 0,56 или 56% - это доля
вариации у зависимая от вариации х и 100%56%=44% вариации у зависимая от вариации
других факторов, не учтенных в модели.
2
34. Для определения статистической значимости коэффициента детерминации используется F– наблюдаемое Фишера по формуле
R n 2F
2
1 R
2
35. F- критическое определяется по таблице распределения Фишера
F , 1 , 2 ,где 1 1, 2 n 2
36. Если , то значим
ЕслиF F , 1 , 2 , то
R
2
значим
37. 5. Метод наименьших квадратов (МНК)
МНК минимизирует сумму квадратовразностей между фактическими и
расчетными значениями зависимой
переменной у.
38. МНК
S ( yi yˆ i ) min2
39. Необходимым условием минимума является равенство нулю ее частных производных по параметрам регрессии. Для линейной регрессии
получаемсистему нормальных уравнений:
40.
nab
x
y
,
i
i
i 1
i 1
n
n
n
a x b x 2 y x .
i
i
i i
i 1
i 1
i 1
n
n
41. Решая систему, получим:
xy x yb 2
2
x (x )
a y b x
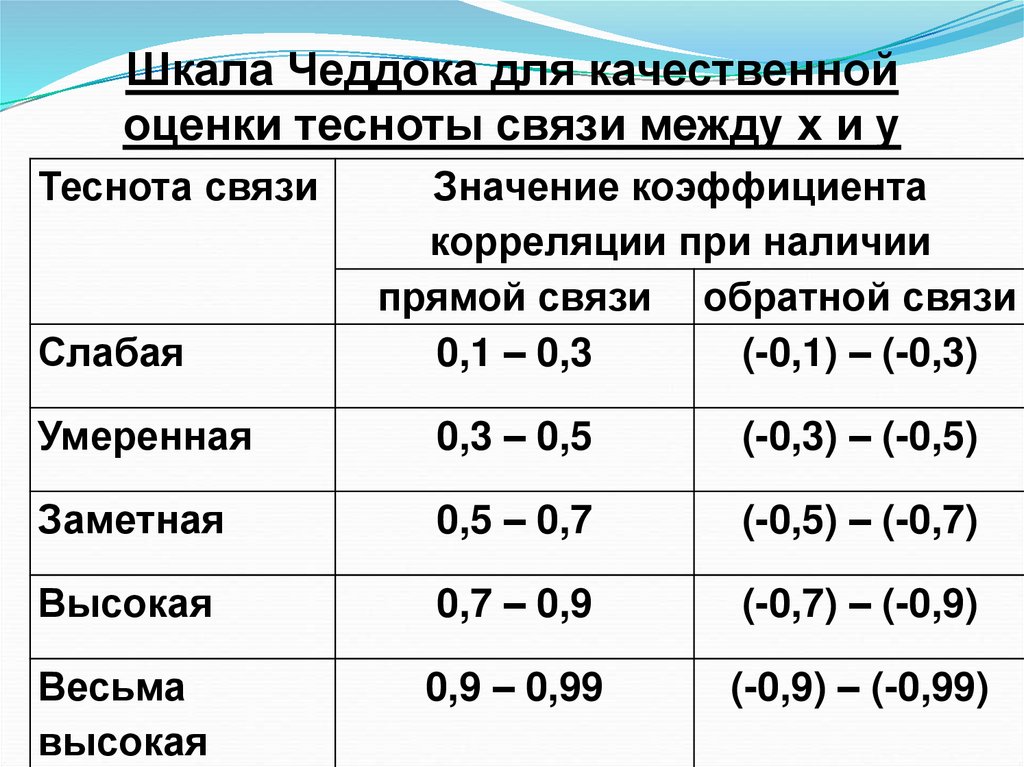
42. Шкала Чеддока для качественной оценки тесноты связи между х и у
Теснота связиСлабая
Значение коэффициента
корреляции при наличии
прямой связи обратной связи
0,1 – 0,3
(-0,1) – (-0,3)
Умеренная
0,3 – 0,5
(-0,3) – (-0,5)
Заметная
0,5 – 0,7
(-0,5) – (-0,7)
Высокая
0,7 – 0,9
(-0,7) – (-0,9)
Весьма
высокая
0,9 – 0,99
(-0,9) – (-0,99)
43. 6. Предпосылки МНК – условия Гаусса-Маркова
1. Математическое ожидание случайногоотклонения i равно нулю для всех
наблюдений M( i )=0.
2. Дисперсия случайного отклонения
постоянная для всех наблюдений
2
D( ) =D( ) =
j
i
44. Постоянство дисперсии отклонения называется гомоскедастичностью. Непостоянство дисперсии отклонения называется
гетероскедастичностью.3. Случайные отклонения i и j
должны быть независимы друг от друга.
Если данное условие выполняется, то
говорят об отсутствии автокорреляции.
4. Случайные отклонения должны быть
независимы от объясняющих переменных.
45. Теорема Гаусса-Маркова
«Если выполняются условия 1- 4, тооценки (a, b), сделанные с помощью МНК,
являются наилучшими линейными
несмещенными оценками параметров(β0,β1),
т.е. они обладают свойствами:
1) несмещенность;
2) эффективность;
3) состоятельность.»
46.
Оценка Θn (тэта) называется состоятельной ,если она сходится по вероятности к значению
оцениваемого параметра Θ при безграничном
возрастании объема выборки.
Несмещенная оценка Θn – это оценка параметра
Θ, математическое ожидание которой равно
значению оцениваемого параметра: М(Θn)=Θ.
Эффективная оценка – это несмещенная оценка,
имеющая наименьшую дисперсию из всех
возможных несмещенных оценок параметра
47.
Лекция № 4(слайды 49-74)
7. Ошибки измерения
48. Средняя ошибка аппроксимации или среднее относительное отклонение расчетных значений от фактических (должно быть не более 8 –
10%)yi yˆ i
1
А
100%
n
yi
49. Коэффициент эластичности показывает, на сколько % изменяется функция y=f(x) при изменении независимой переменной х на 1 %.
Эy x bx
y
50.
Мерой разброса переменной у служитстандартная ошибка регрессии S 2 S 2
1
1
2
2
S
ei
yi yˆ i
n 2
n 2
2
1
2
S
ei
n 2
e
51. Стандартные ошибки коэффициентов регрессии оцениваются по формулам:
x Sn x x
2
S
2
a
2
2
, S
2
b
S
2
n x x
2
52. Оценка значимости коэффициентов регрессии с помощью t – наблюдаемого Стьюдента по формулам:
ab
t a , tb
Sa
Sb
53. t- критические определяются по таблицам распределения Стьюдента Если , то коэффициенты a и b значимы
t- критические определяются по таблицамраспределения Стьюдента
,n 2
t
t t
и t t
Если a
, n 2
b , ,n 2
то коэффициенты a и b значимы
54. Предсказание и прогнозирование на основе линейной модели регрессии
Поиск значений У для Х, находящихсямежду известными значениями,
называется предсказанием.
Прогнозирование – это оценка значений
У для некоторого будущего набора
независимых переменных.
55. Для предсказания достаточно поставить в уравнение регрессии нужное значение х. Для прогноза используется понятие доверительной
вероятности0,9; 0,95; 0,99
и уровня значимости
1 0,1; 0,05; 0,01
56. Доверительные интервалы
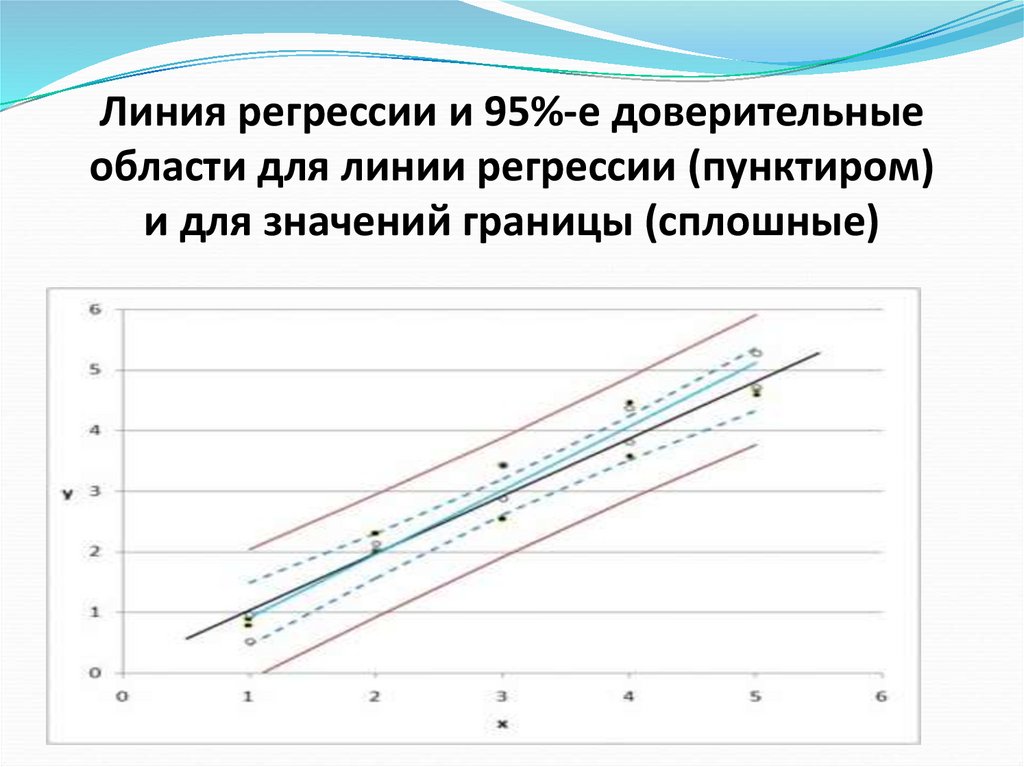
57. Линия регрессии и 95%-е доверительные области для линии регрессии (пунктиром) и для значений границы (сплошные)
58. Доверительный интервал для y
yˆ t12
, n 2
S yˆ y yˆ t1
2
, n 2
S yˆ
59. Доверительный интервал для
yˆ t12
, n 2
S y y yˆ t1
2
y
, n 2
Sy
60. Пояснения к формулам доверительных интервалов (m –кратность измерений у)
S2
e
S yˆ S e
yi yˆ
2
n 2
x x
x x
1 1
x x
m n x x
1
n
2
2
i
2
S y Se
2
i
61. Коэффициент детерминации для линейной регрессии
R2 = r 2показывает долю общей вариации
(дисперсии) зависимой переменной y,
обусловленной регрессией или
изменчивостью объясняемой переменной x.
62. 9. Нелинейные модели регрессии и их линеаризация.
,9. Нелинейные модели регрессии и
их линеаризация.
Экспоненциальная регрессия
y e
ax b
Линеаризующие преобразования
x' x
y ' ln y
63. Параметры уравнения экспоненциальной регрессии
bn
n
n
i 1
i 1
i 1
2
n ( xi ln yi ) xi ln yi
n xi xi
i 1
i 1
n
n
2
n
n
1
1
a ln yi b xi
n i 1
n i 1
64. Логарифмическая регрессия
,Логарифмическая регрессия
y a b ln x
x ' ln x
y' y
65. Параметры уравнения логарифмической регрессии
bn
n
n
i 1
i 1
i 1
2
n (ln xi yi ) ln xi yi
n (ln xi ) ln xi
i 1
i 1
n
n
2
n
n
1
1
a yi b ln xi
n i 1
n i 1
66. Решение задач на компьютере
Microsoft ExcelВычислениевыборочнойсредней
1
x xi
n
x СРЗНАЧ ( массив х)
67. Выборочная дисперсия (вариация)
21
2
2
d B DB var( x) xi x x ( x)
n
d B ДИСПР( массив х)
68. Исправленная дисперсия
nS
dB
n 1
2
x
x
i
x
n 1
S ДИСП ( массив х)
2
x
2
2
n
2
[x x ]
n 1
69. Стандартное отклонение
Sx S2
x
x
i
x
2
n 1
S x СТАНДОТКЛОН ( массив х)
70. Коэффициент корреляции Пирсона
rxyy y
~y y
i
2
2
i
xy x y
x x y y
2
2
2
2
rxy PEАRSON ( массив х, массив у )
КОРРЕЛ ( массив х, массив у )
71. Коэффициенты уравнения регрессии
a = ОТРЕЗОК (массив х, массив у)b = НАКЛОН (массив х, массив у)




























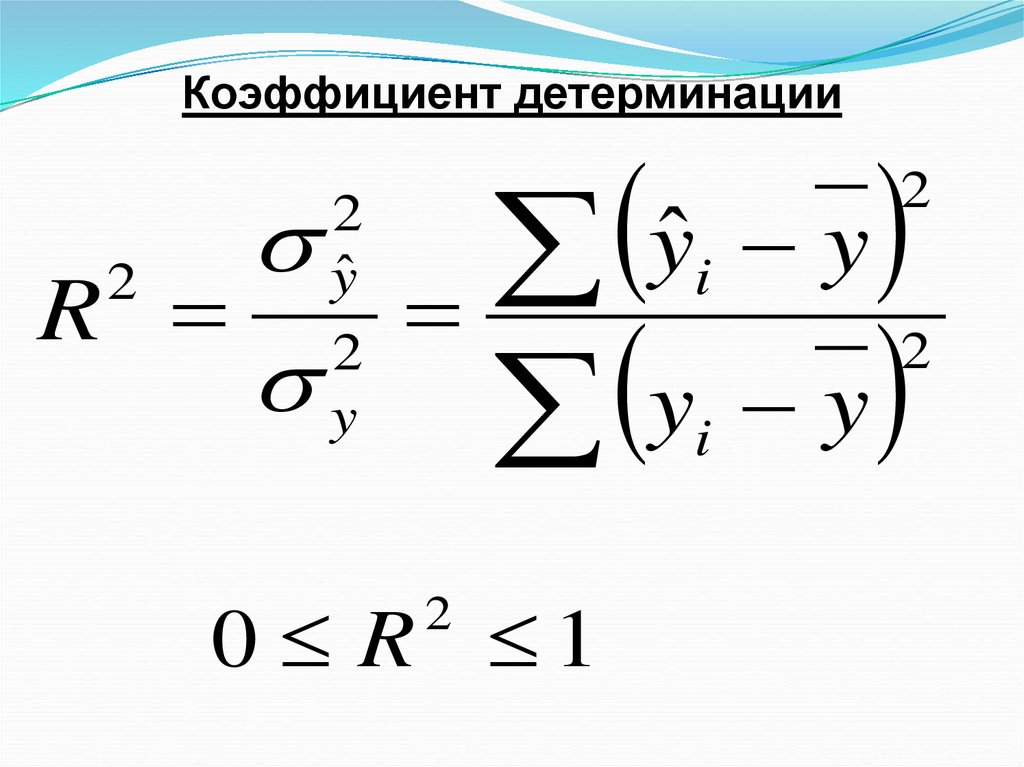
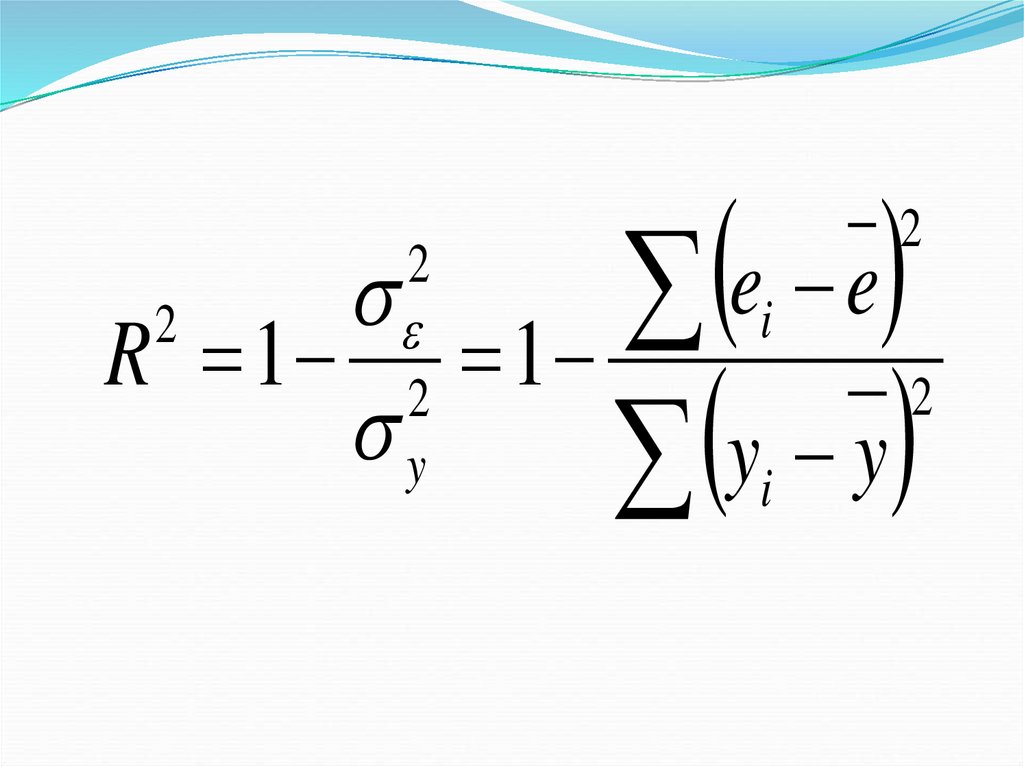



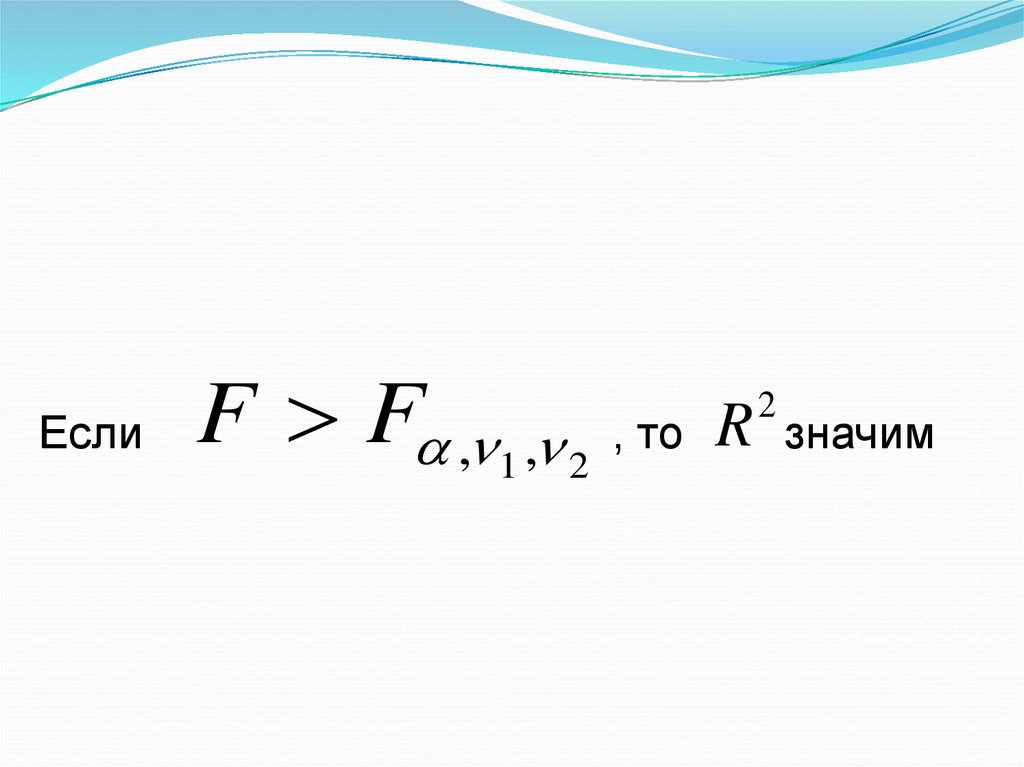



































 Математика
Математика Экономика
Экономика








