Решение тригонометрических уравнений

1.

2. Решение тригонометрических уравнений.

Удачи!
sin 4x sin
– sin
2x1 = 0
x
=
cos x = 0
Решение
тригонометрических
уравнений.

3.

Цели урока:
1. Образовательные – обеспечить повторение и
систематизацию материала темы. Научить при
решении уравнений применять формулы понижения
степени. Создать условия контроля усвоения знаний
и умений.
2. Развивающие – способствовать формированию
умений применять приемы сравнения, обобщения,
выявления главного, переноса знаний в новую
ситуацию; способствовать развитию
математического кругозора, мышления и речи,
внимания и памяти.
3. Воспитательные – содействовать воспитаю общей
культуры, умения общаться, интереса к математике и
ее приложениям, активности, мобильности.

4.

«Деятельность –
единственный путь к
знанию».
Бернард Шоу

5. Устная работа.

Простейшие тригонометрические
уравнения
1. При каком значении а
уравнение cosx = a имеет
решение?
2. При каком значении а
уравнение sinx = a имеет
решение?
3.Что такое arccosa?
4. Что такое arcsina?
5. В каком промежутке
находится arccos a ?
7. В каком промежутке
находится значение а?
9. Чему равняется
arccos ( - a)?
6. В каком промежутке
находится arcsin a ?
8. В каком промежутке
находится значение а?
10.Чему равняется
arcsin ( - a)?

6. Устная работа.

Простейшие тригонометрические
уравнения
11. В каком промежутке
находится arctg a?
12. В каком промежутке
находится arcctg a?
13. Каково будет решение
уравнения cos x = a?
14. Каково будет решение
уравнения sin x = a?
15. Каково будет решение
уравнения cos x = - a?
16. Каково будет решение
уравнения sin x = - a?
17. Какой формулой
выражается решение
уравнения tgx = а?
18. Какой формулой
выражается решение
уравнения tgx = - а?

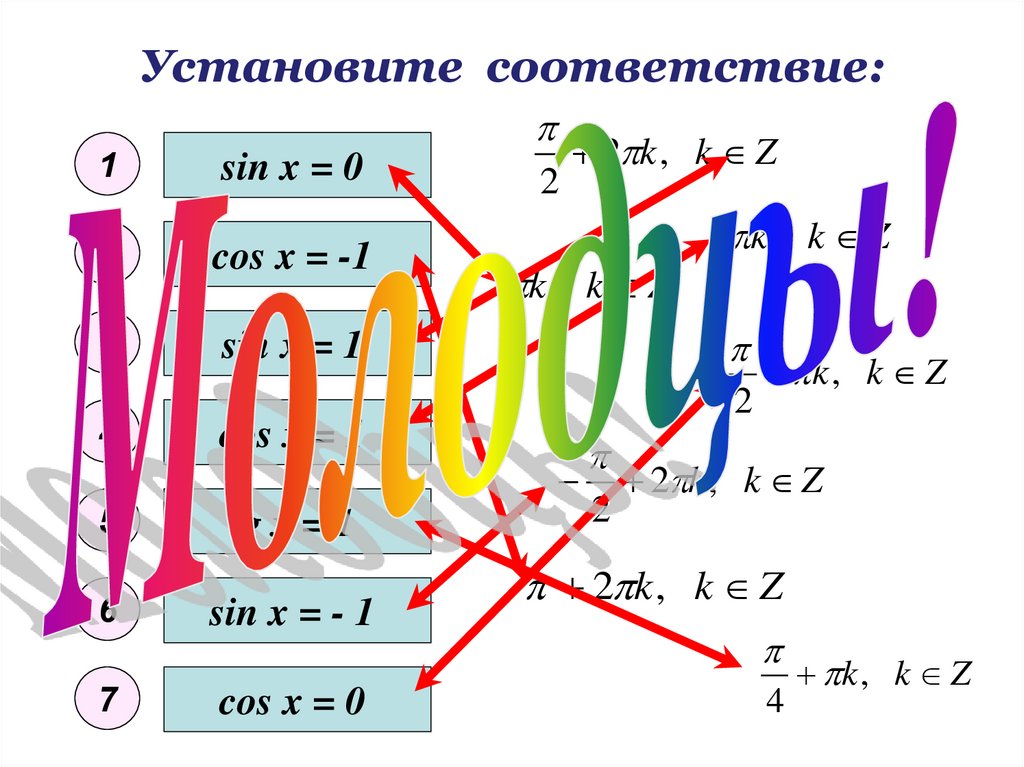
7. Установите соответствие:

1
sin x = 0
2
cos x = -1
3
sin x = 1
4
5
6
7
cos x = 1
tg x = 1
sin x = - 1
cos x = 0
2
2 k , k Z
k , k Z
2 k , k Z
2
2
k , k Z
2 k , k Z
2 k , k Z
4
k , k Z

8. Установите соответствие:

1
sin x = 0
2
cos x = -1
3
sin x = 1
4
5
6
7
cos x = 1
tg x = 1
sin x = - 1
cos x = 0
2
2 k , k Z
k , k Z
2 k , k Z
2
2
k , k Z
2 k , k Z
2 k , k Z
4
k , k Z

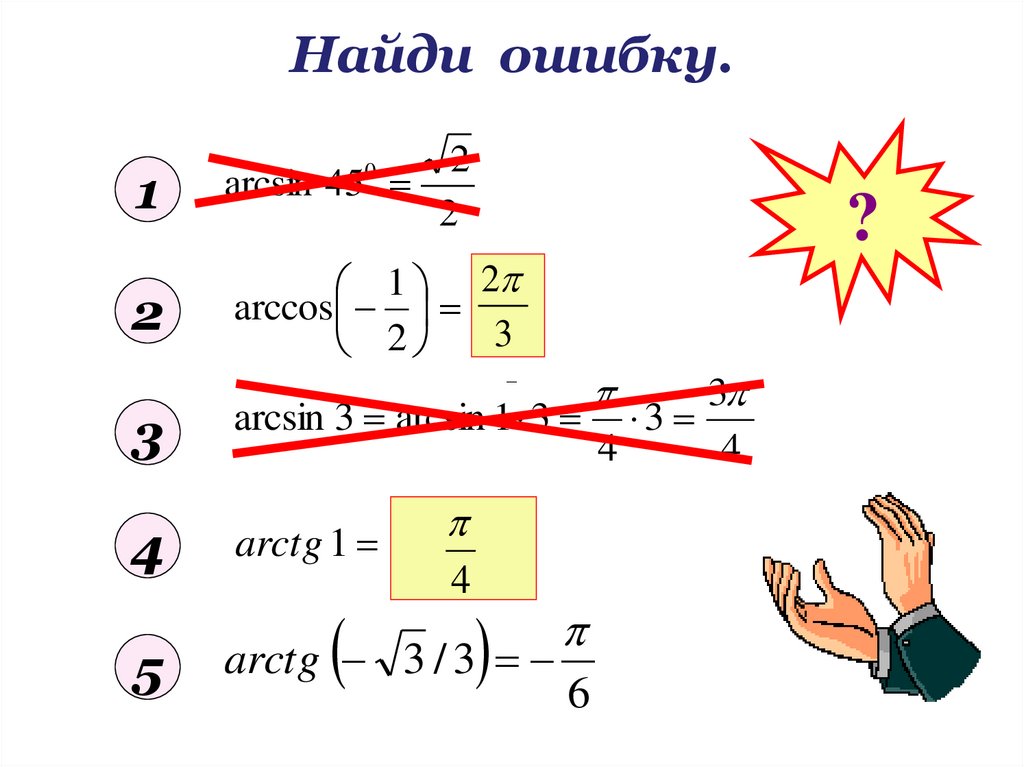
9. Найди ошибку.

1
2
arcsin 45
2
2
1 2
arccos
33
2
0
?
3
3
arcsin 3 arcsin 1 3 3
4
4
4
arctg 1 arctg
4 4
5
arctg 3 / 3
6

10. Методы решения тригонометрических уравнений.

Необходимо выбрать соответствующий
Методы
решения
прием
для решения
уравнений.
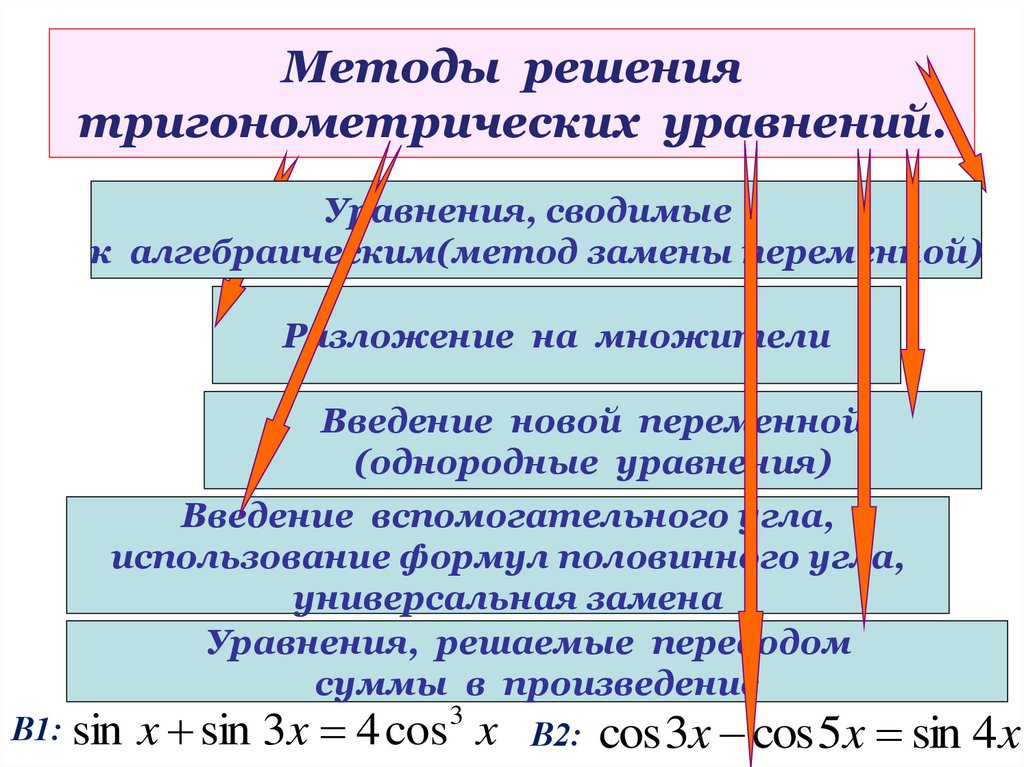
тригонометрических уравнений.
Уравнения сводимые
к алгебраическим(метод замены переменной)
Вариант 1:
c o s 2 x sin x sin x 0 , 2 5
Вариант 2:
3 cos 2 x 5 cos x 1
2

11. Методы решения тригонометрических уравнений.

Уравнения, сводимые
к алгебраическим(метод замены переменной)
Разложение на множители
Вариант 1:
3 sin x 3 sin x cos x 0
Вариант 2:
3 cos x 3 sin x cos x 0
2
2

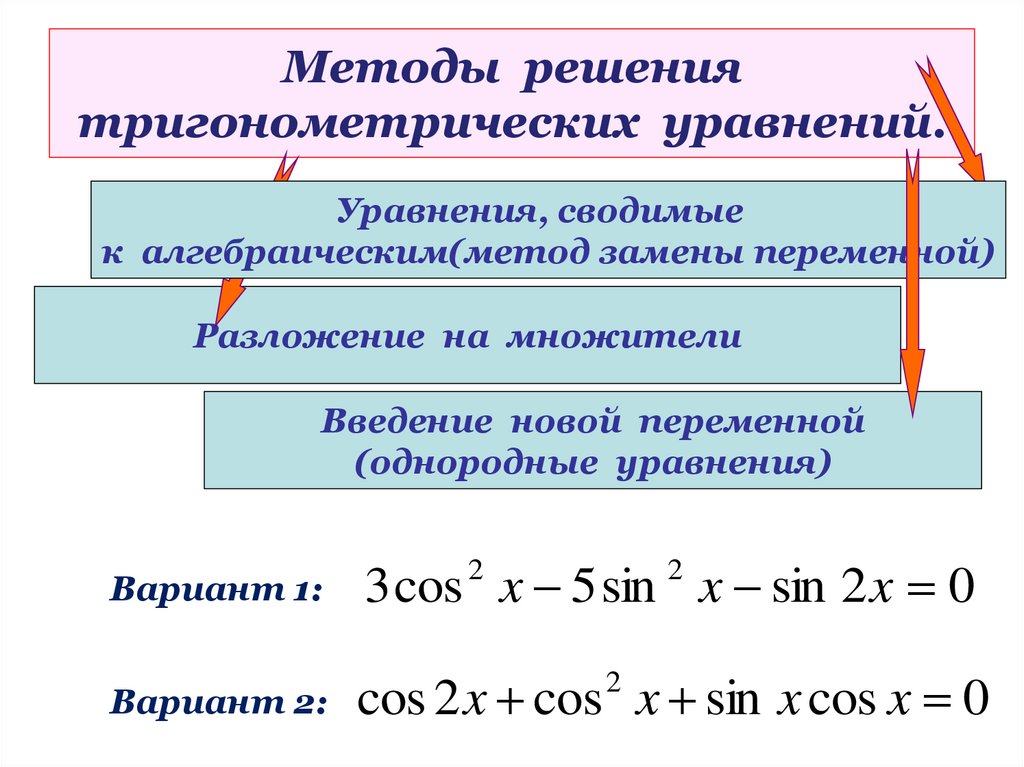
12. Методы решения тригонометрических уравнений.

Уравнения, сводимые
к алгебраическим(метод замены переменной)
Разложение на множители
Введение новой переменной
(однородные уравнения)
Вариант 1:
3 cos x 5 sin x sin 2 x 0
Вариант 2:
cos 2 x cos x sin x cos x 0
2
2
2

13. Методы решения тригонометрических уравнений.

Уравнения сводимые
к алгебраическим(метод замены переменной)
Разложение на множители
Введение новой переменной
(однородные уравнения)
Введение вспомогательного угла,
использование формул половинного угла,
универсальная замена
Вариант 1:
3 sin x cos x 1
Вариант 2:
2 sin x cos x 2

14. Методы решения тригонометрических уравнений.

Уравнения, сводимые
к алгебраическим(метод замены переменной)
Разложение на множители
Введение новой переменной
(однородные уравнения)
Введение вспомогательного угла,
использование формул половинного угла,
универсальная замена
Уравнения, решаемые переводом
суммы в произведение
В1: sin x sin 3 x 4 cos 3 x В2: cos 3x cos 5x sin
4x

15. Применение формул понижения степени.

2
2sin
x + cos 4x = 0

16. Применение формул понижения степени.

В1:
sin x sin 2 x sin 3x 1,5
2
2
2
В2:
cos x cos 2 x cos 3x 1,5
2
2
2

17. Формулы квадрата половинных углов:

Применение формул понижения
степени.
Формулы квадрата половинных углов:
1 cos
1 cos
2
2
cos
sin
2
2
2
2
Формулы понижения степени:
1
sin 1 cos 2
2
1
cos 1 cos 2
2
2
2
2sin2 x + cos 4x = 0
В1:
sin x sin 2 x sin 3x 1,5
2
2
В2:
2
cos x cos 2 x cos 3x 1,5
2
2
2

18. Формула успеха.

Как добиться успеха?
Смелость + уверенность в собственных
силах + профессионализм + инициатива +
творчество + способность доводить дело до
конца + высокий уровень развития +…..+
(каждый для себя добавит особый
компонент)

19. Домашнее задание:

№ 207 (а, б, в, д)
стр. 389