Похожие презентации:
Собственные значения и собственные векторы
1.
2.
Вспоминаем пример3.
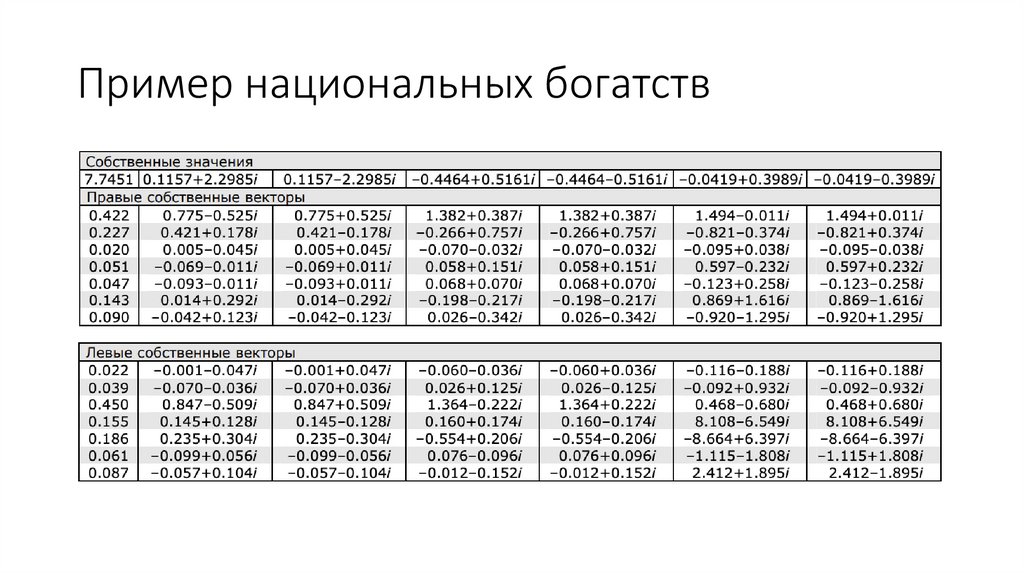
3.6. ВСЕ СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕВЕКТОРЫ: ПРИМЕР НАЦИОНАЛЬНЫХ БОГАТСТВ ИЗ ГЛ. 2
• Для всех собственных значений представлены как левые, так и
правые собственные векторы.
• Для λ = λmax левый собственный вектор – двойственный правому
собственному вектору, как и способ измерения
противоположности влияния по отношению к свойству, которое
нами использовалось при проведении сравнений.
• Когда имеется согласованность, эти два главные собственные
векторы точно взаимо обратны. Это отношение имеет место
между главными левым и правым собственными векторами всех
обратно симметричных матриц размера 2 x 2 и 3 x 3 .
Матрица А называется обратно-симметричной, если для любых i и k выполняется
соотношение a ki = 1 / a ik
4.
Пример национальных богатств5.
3.7. КОНСЕНСУС И МЕТОД ДЕЛЬФИ• Важной особенностью, относящейся к высказыванию суждений
несколькими лицами, является то, каким образом достигается
консенсус из их суждений. Процесс достижения консенсуса
может быть использован для убеждения людей в том, что их
интересы принимаются во внимание. Поэтому для наших целей
консенсус означает увеличение уверенности в значениях
приоритетов посредством привлечения нескольких экспертов для
приведения приоритетов в соответствие с предпочтениями
большинства.
6.
• Есть несколько работ, проведенных по проблеме достиженияконсенсуса: Кемени и Снэлл, чья работа была обобщена Богартом,
использовали аксиоматический подход для разработки метода
достижения консенсуса в случае слабого упорядочения
(предпочтительно – 1, равенство – 0, непредпочтительно – -1)
множества объектов несколькими лицами.
• Они доказали, что существует единственная функция расстояния,
удовлетворяющая всем аксиомам.
• Эта функция использована для получения матрицы консенсуса
посредством поиска для каждого элемента величины, которая
минимизирует сумму квадратов расстояний до каждого
соответствующего элемента матриц суждений, построенных
несколькими лицами. Результатом может быть не целое число;
некоторые исследователи на практике округляют числа до ближайшего
целого. Величина, полученная таким образом, называется средней.
7.
• Функция расстояния также используется для получения матрицымедианных значений. Каждый элемент этой матрицы
минимизирует сумму расстояний до соответствующих элементов
матриц суждений.
• Хотя как среднее, так и медиана представляются разумными
способами достижения консенсуса, среднее обеспечивает
способ «приравнивания объектов», которые сравниваются, в то
время как медиана предлагает способ «отбора среди
экспертов», высказывающих суждение. В нашем случае
применяется геометрическое среднее.
8.
• Богарт обобщил подход функции расстояния на все частичныеупорядочения множества, распространив предыдущую работу на
полуупорядочения и интервальные упорядочения и даже на
нетранзитивные упорядочения. После доказательства
единственности функции расстояния, удовлетворяющей
разумному набору аксиом
9.
Среди прочих вещей он показал следующее:1. Среднее набора упорядочений в множестве всех антисимметричных
упорядочений удовлетворяет правилу решения (называемому
правилом сильного большинства), согласно которому a
предпочтительнее b , если число предпочитающих элемент a
элементу b минус число предпочитающих b элементу a больше
половины числа лиц, производящих суждение. Правило ведет к
единственному среднему набора.
2. Упорядочение правилом большинства (при котором a
предпочтительнее b, если это утверждает большинство людей,
высказывающих суждение) для множества антисимметричных
упорядочений является медианой множества. Эта медиана
единственна, если число экспертов, предпочитающих элемент a
элементу b , не равно числу экспертов, предпочитающих b элементу
a.
10.
В данной работе консенсус достигается по различнымнаправлениям.
• Решающим является количество информации, имеющейся для
произведения суждений. При поиске консенсуса
предпочтительно взаимодействие экспертов. Хорошо
информированное лицо может существенно повлиять на мнение
лица, обладающего меньшей информацией. Дискуссия может
помочь сблизить суждения и обеспечить информацией самих
экспертов для применения метода установления приоритетов.
• Следовательно, наш подход к консенсусу заключается в
применении метода нахождения приоритетов для нескольких
лиц, вовлекаемых в соответствии с содержанием их суждения.
11.
Факторами, влияющими на суждение, могут быть:относительный интеллект (однако, измеренный), опыт,
информированность, глубина знаний, опыт в смежных областях,
личный интерес в исследуемом вопросе и т. д. Если к суждению
этих людей мы относимся с большим доверием, то полученный
приоритет используется для взвешивания окончательного
результата, полученного из суждения каждого лица, и затем общий
взвешенный приоритет определяется обычным путем.
С другой стороны, если степень доверия к суждениям,
произведенным экспертами, низка, то следует применять
геометрическое среднее их индивидуальных суждений в каждой
матрице сравнений.
Средним геометрическим нескольких положительных вещественных чисел называется
такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не
изменилось.
12.
• В промежуточных ситуациях можно прибегнуть к комбинацииэтих двух процедур, однако подробно эту проблему мы не
изучали.
• Другой областью исследования является сравнение результатов,
полученных этим путем и в других работах. Как представить
групповое суждение удовлетворительным образом, когда опыт и
суждения людей различаются? Чьи мнения должны быть более
серьезно приняты во внимание и почему? – важные задачи
социальных исследований и анализа конфликтов.
13.
• Представляется, что мысль, развитую и оцененную одной группой, следуетпередать другой группе для обсуждения и изменения суждения. Но
конечный результат может все же еще сильно меняться.
• Поэтому переговоры и приход к соглашению должны быть внутренней
процедурой группового согласия. Не следует выносить третейского решения
по приоритетам, используя суждения привилегированной группы по
сравнению с остальными. Другими словами, выявление удобной и
пригодной для работы математической схемы для задачи не решает
автоматически ее социальных сложностей.
• Тем не менее эта схема может упростить процесс выявления того, где
должны быть достигнуты наиболее плодотворные компромиссы и
соглашения. Если социальная задача требует арбитража, то посредник
должен тщательно оценить потребности и влияния групп перед тем, как
указать, где следует пойти на компромиссы. Возможно, наиболее
многообещающим вкладом иерархического анализа является
использование в структурировании задачи с самого начала взаимно
конфликтующих групп, а не пассивных свидетелей, а затем приход к
соглашению через численные входные данные.
14.
Метод Дельфи• сильно зависит от концепции консенсуса
• Этот метод является хорошо известным процессом, который
позволяет анализировать задачи, оценивать величины и
прогнозировать перспективную пользу от управления.
15.
Основные различия между методомДельфи и иерархическим анализом
1. Анонимное по сравнению с описанным групповое обсуждение. В
методе Дельфи каждый участник группы отвечает анонимное на
заранее подготовленную анкету, чтобы избежать
непропорционального влияния сильных личностей. В
иерархическом анализе критерии и суждения устанавливаются в
основном открытым групповым процессом.
2. Корректировка представляет собой последовательность туров по
сравнению с динамическим обсуждением. В методе Дельфи должен
быть дан обзор результатов анкетирования, а корректировку
требуется провести вновь на анонимной основе. В иерархическом
анализе при построении иерархии и произведении суждений
используется динамическое обсуждение посредством взаимного
соглашения и пересмотра взглядов. Участники пытаются
представить свои аргументы открыто.
16.
3. Анкета в качестве основы для суждений по сравнению сиерархической структурой. В методе Дельфи вид анкеты
предполагает выбор переменных, включенных лицом, создающим
анкету. В иерархиях группа решает, какие переменные производят
воздействие на требуемое суждение. Вначале все предложенные
переменные принимаются. Позже в процедуре некоторыми из них
можно пренебречь из-за низкого приоритета, приписанного им
группой.
4. Статистический и количественный анализ по сравнению с
качественным анализом. Метод Дельфи требует численных ответов,
которые должны быть подвергнуты статистическому анализу в
качестве основы для следующего тура. Для иерархий в суждения
включены абсолютные числа от 1 до 9, отражающие качественные
суждения о парном сравнении и используемые как часть получения
точной оценки для основной шкалы отношений. Согласованность
как необходимое условие, обосновывающее шкалирование
реальности, является важным критерием
17.
В обоих случаях процесс анализа задачи улучшает качествосуждений, однако метод иерархического анализа расчленяет
суждение на элементарные компоненты и поэтому лучше подходит
к познавательной манере человека. Другим важным итогом
является определение группой множества важных переменных,
что придает ей большую уверенность в релевантности своих
суждений. Эта процедура полезна для уменьшения
рассогласований открытым динамическим образом. Многие
исследователи, пользующиеся ею на практике, рекомендовали ее
использование при планировании и прогнозировании как краткую
и простую процедуру, отражающую мнения участников с весьма
эффективным результатом.
18.
ГЛАВА 4 ИЕРАРХИИ И ПРИОРИТЕТЫОпределение 4.1. Упорядоченным множеством называют любое
множество S с бинарным отношением ≤ , которое удовлетворяет
законам рефлексивности, антисимметричности и транзитивности:
• Рефлексивность: для всех x , x ≤ x .
• Антисимметричность: если x ≤ y и y ≤ x, то x = y .
• Транзитивность: если x ≤ y и y ≤ z, то x ≤ z .
Для любого отношения x ≤ y (читается: x предшествует y ) такого типа
можно определить x < y , что означает x ≤ y и x ≠ y . Говорят, что y
покрывает (доминирует) x , если x < y и если x < t <y невозможно ни для
какого t.
Упорядоченные множества с конечным числом элементов могут быть
удобно представлены направленным графом.
19.
Определение 4.2. Просто или вполне упорядоченное множество(также называемое цепью) есть упорядоченное множество со
следующим дополнительным свойством: если x, y ∈ S, то или x ≤ y ,
или y ≤ x
Определение 4.3. Подмножество E упорядоченного множества S
называют ограниченным сверху, если существует элемент s∈S
такой, что x ≤ s для любого x ∈ E . Элемент s называют верхней
границей E . Говорят, что E имеет супремум или наименьшую
верхнюю границу в S , если E имеет верхние границы и у
множества верхних границ U имеется элемент u_1 такой, что
u_1 ≤ u для всех u ∈ U. Элемент u_1 – единственный и называется
супремумом E в S .
Вполне упорядоченное множество — упорядоченное множество M такое, что в любом его
подмножестве есть минимальный элемент.
20.
21.
22.
С точки зрения оптимизации для распределения ресурсов междуэлементами необходимо учитывать также все взаимосвязи между
ними. Аналитически взаимосвязь может принять вид отношений
типа вход–выход.
Например, имеющих место при взаимном обмене продукцией
между отраслями промышленности. Отрасль с более высоким
приоритетом может зависеть от потока продукции, выпускаемой
отраслью с более низким приоритетом. В рамках оптимизации
приоритет элементов позволяет определить целевую функцию,
которую затем следует максимизировать, а другие 72 иерархии
позволяют получить информацию, касающуюся связей, например
отношений типа вход–выход.
23.
Решение основной задачи24.
Композиция приоритетов включает взвешивание и суммирование. Это требуетнезависимости критериев на каждом уровне, в противном случае один
элемент может получить некоторый приоритет относительно некоторого
признака и дополнительный приоритет, вызванный перекрыванием этого
признака с другим признаком, что вызовет двойной учет.
В простых терминах множество признаков или критериев называют
независимым, если возможна взаимозаменяемость любой пары
безотносительно влияния других. Иными словами, критерии независимы,
если между ними нет взаимодействия.
25.
Принцип иерархической композиции:аддитивность взвешивания
26.
27.
Приоритет элемента любого уровня равен сумме его приоритетов вкаждом подмножестве сравнения, которым он принадлежит;
иногда каждый из приоритетов взвешивается лишь частью
элементов уровня, которые принадлежат данному подмножеству,
и приоритетом подмножества. Получающееся множество
приоритетов элементов этого уровня затем нормализуется
посредством деления на сумму приоритетов элементов. Приоритет
подмножества на уровне равен приоритету доминирующего
элемента на следующем уровне.
28.
29.
4.3. ДЕКОМПОЗИЦИЯ И АГРЕГИРОВАНИЕ(ПОСТРОЕНИЕ КЛАСТЕРОВ)
Существуют два фундаментальных подхода, в которых может быть
использована идея иерархии. 75
Первый подход сейчас уже ясен: реальный мир следует моделировать
иерархически.
Второй подход, вероятно, является более фундаментальным, чем первый, и
свидетельствует о реальной силе иерархий в природе. Он заключается в
расчленении рассматриваемых вещей на большие группы или кластеры,
которые далее расчленяются на меньшие кластеры и т. д. Тогда целью будет
получение приоритетов всех элементов посредством группирования. Это
намного более эффективный процесс, чем обработка всех элементов
совместно. Следовательно, несущественно, думаем ли мы, что иерархии
внутренне присущи природе, как утверждают некоторые исследователи, либо
мы просто используем их из-за ограниченной способности обрабатывать
информацию. В любом случае они представляют собой очень эффективный
способ исследования сложных проблем.
30.
Полезным способом исследования большого числа элементов, попадающихна один из уровней иерархии, является группирование их в кластеры в
соответствии с их относительной важностью.
Таким образом, можно иметь кластер самых важных (самых подобных, или
близких) элементов, другой кластер элементов умеренной важности, и
третий – элементов с малой важностью. Затем сравниваются попарно
относительное воздействие кластеров на соответствующий критерий из
расположенного выше уровня.
Группирование в кластеры может различаться от критерия к критерию. После
анализа кластеров элементы в каждом кластере попарно сравниваются по их
относительной важности в этом кластере. Если их слишком много, то они
вновь могут быть сгруппированы в кластере. Таким образом, каждый элемент
принадлежит нескольким кластерам и получает несколько весов из
различных кластеров. Не существует альтернативы этому процессу
группирования и декомпозиции, особенно, когда нужно сохранить высокую
согласованность. Принимая это за факт, не следует пугаться размерности
задачи, поскольку уже известно, как можно справиться с этой проблемой. Мы
весьма успешно применяли этот процесс во многих примерах. Легко показать
математически, что группировкой в кластеры можно получить те же самые
результаты, что и при общем подходе.
31.
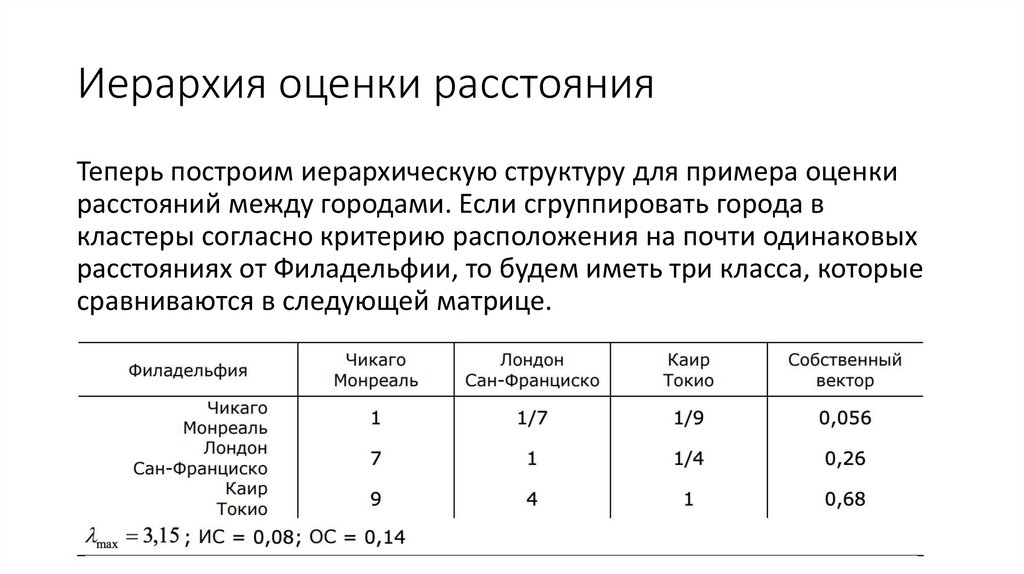
Иерархия оценки расстоянияТеперь построим иерархическую структуру для примера оценки
расстояний между городами. Если сгруппировать города в
кластеры согласно критерию расположения на почти одинаковых
расстояниях от Филадельфии, то будем иметь три класса, которые
сравниваются в следующей матрице.
32.
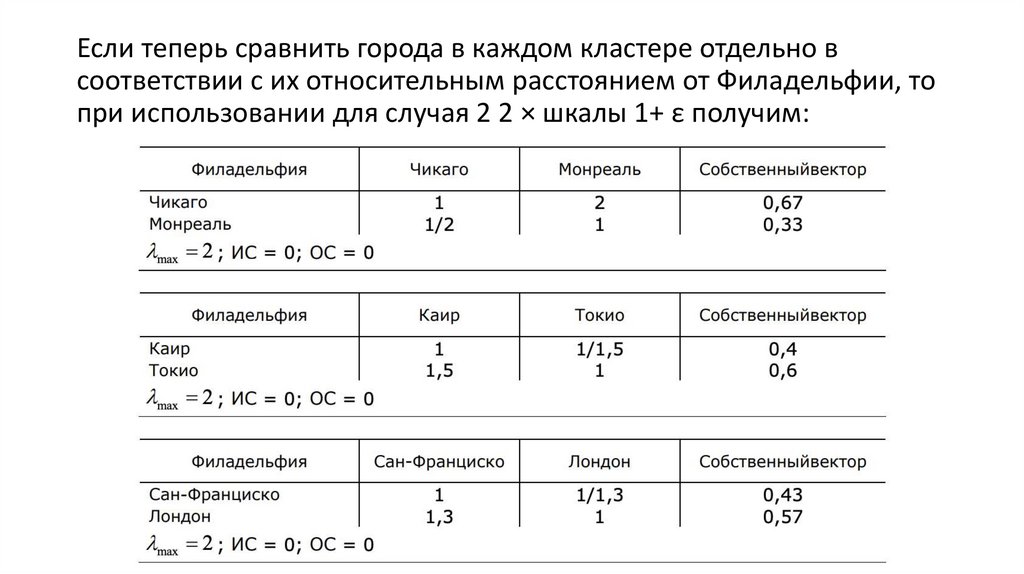
Если теперь сравнить города в каждом кластере отдельно всоответствии с их относительным расстоянием от Филадельфии, то
при использовании для случая 2 2 × шкалы 1+ ε получим:
33.
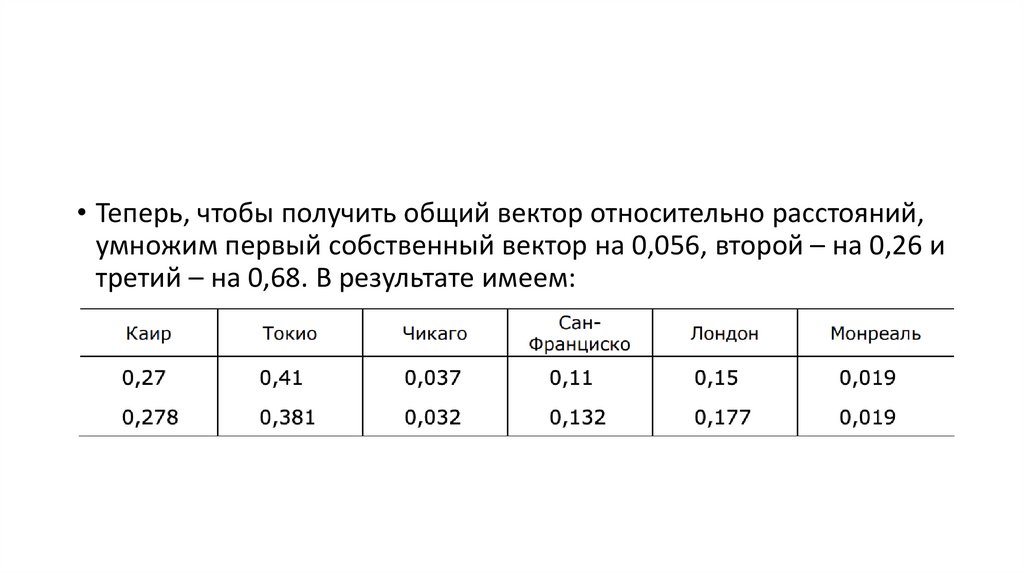
• Теперь, чтобы получить общий вектор относительно расстояний,умножим первый собственный вектор на 0,056, второй – на 0,26 и
третий – на 0,68. В результате имеем:
34.
Пример национальных богатств каккластера
35.
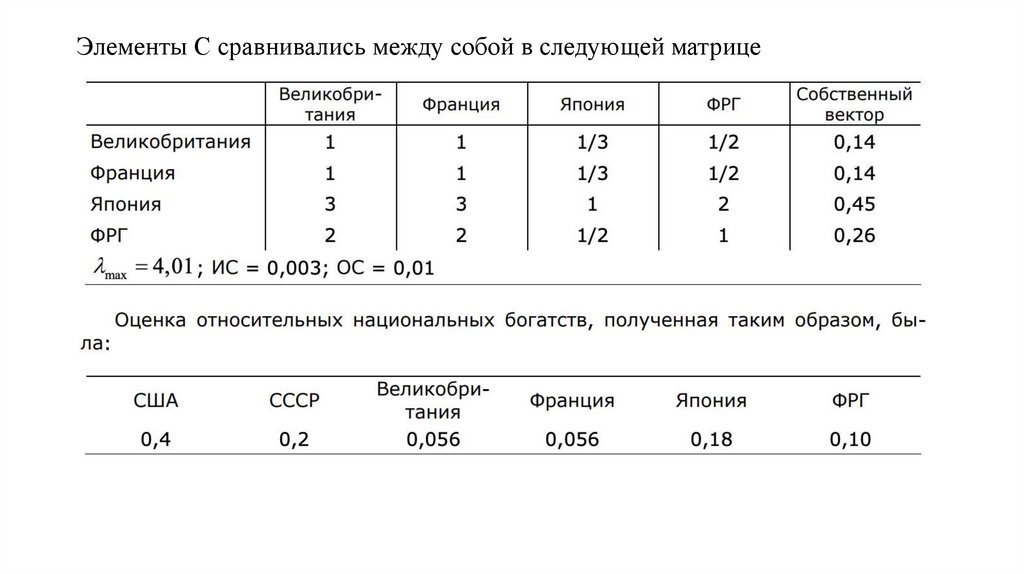
Элементы С сравнивались между собой в следующей матрице36.
37.
• Придание иерархической формы сложной задаче посредствомгруппировки в кластеры имеет два преимущества: 1. Большая
эффективность при проведении парных сравнений. 2. Большая
согласованность при условии ограниченной способности мозга
сравнивать больше, чем 7 2 ± элементов одновременно.
38.
Пример про часыСтр. 78
39.
4.4. СТАНДАРТИЗАЦИЯ ИЗМЕРЕНИЯЭЛЕМЕНТОВ ИЗ БОЛЬШОГО КЛАССА
Элементы сначала упорядочиваются согласно их относительной
сравнимости и группируются в классы.
В каждом классе величина меры элементов – одного порядка. Если
два класса различаются более, чем на один порядок, то делается
попытка расчленения или декомпозиции элементов класса,
получившего более высокое измерение, на более легкие
элементы. В противном случае элементы меньшего класса
агрегируются, образуя один большой элемент из более высокого
класса. Если ни одна из этих альтернатив невозможна для перехода
из одного класса в другой, то в процессе сравнения вводятся
промежуточные между двумя классами дополнительные
элементы.
40.
Для стандартизации измерения между классами используетсянаибольший элемент в классе элементов с меньшим весом и
наименьший элемент в следующем большем классе. Для
повышения точности можно также взять наименьший элемент
следующего класса в качестве наибольшего элемента в классе
элементов с меньшими весами. Таким образом, вес элемента в
обоих классах может быть применен для стандартизации весов
обоих классов. При этом образуется один класс со всеми
соответствующим образом взвешенными элементами. Процедура
затем проводится по всем классам, и таким образом мы получаем
меру, определенную на большом числе элементов в множестве.
41.
4.5. СОГЛАСОВАННОСТЬ ИЕРАРХИИОбобщим измерение согласованности на всю иерархию.
Процесс заключается в том, что индекс согласованности,
полученный из матрицы парных сравнений, умножается на
приоритет свойства, относительно которого проведено сравнение,
и к этому числу добавляются аналогичные результаты для всей
иерархии. Затем данная величина сравнивается с соответствующим
индексом, который получен как сумма случайно сформированных
индексов, взвешенных посредством соответствующих приоритетов.
Отношение должно находиться в окрестности 0,10, чтобы не
появилось сомнений в усовершенствовании фактического
функционирования и в суждениях.
42.
4.6. ИНТЕРПРЕТАЦИЯ ПРИОРИТЕТОВ СПОМОЩЬЮ ТЕОРИИ ГРАФОВ






































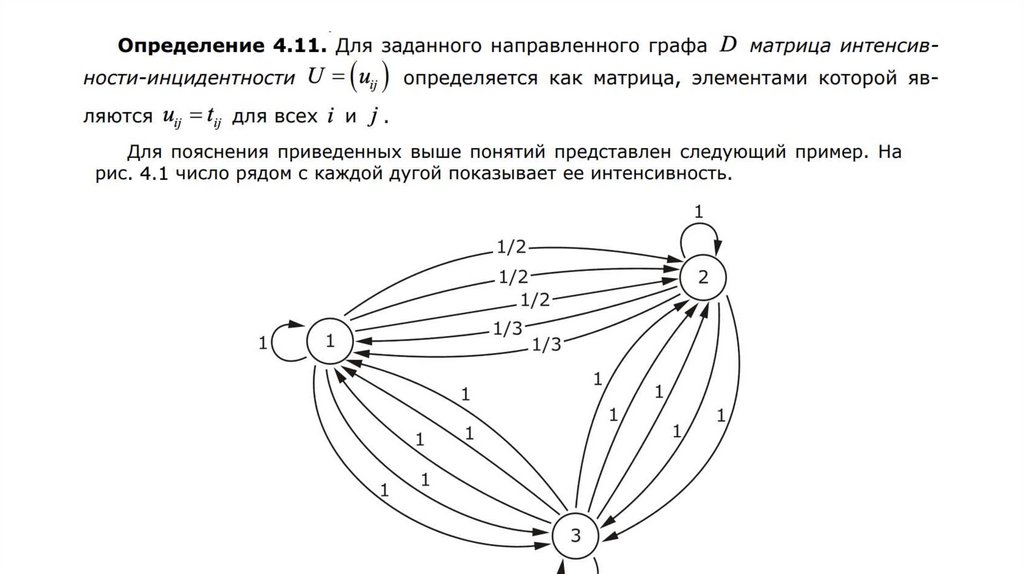


 Математика
Математика








