Собственные значения и собственные векторы матрицы

1.

Лекция №10
Лектор: доц. Лаптева Надежда Александровна
Тема: Собственные значения и
собственные векторы матрицы

2.

Пусть
A - матрица, x
- вектор,
- число.
Рассмотрим уравнение
Ax x.
называется собственным
значением, x - собственным
вектором.
Такое преобразование изменяет
длину вектора в раз.

3.

Например, если 2,то Ax 2 x,
т.е. длина вектора x увеличивается в
2 раза.
Если же
x
1
,
2
то длина вектора
уменьшается в 2 раза.

4.

Рассмотрим
a11
A
a21
A(2 2).
a12
,
a22
x1
x .
x2
Запишем матричное уравнение в
координатной форме.

5.

Ax x
a11 a12 x1 x1
;
a
21 a22 x2 x2
a11 x1 a12 x2 x1 ,
a21 x1 a22 x2 x2 .
Преобразуем
(a11 ) x1 a12 x2 0,
a21 x1 (a22 ) x2 0.

6.

Получилась система линейных
однородных уравнений. Такая
система всегда имеет нулевое
решение. Нас интересует случай,
когда система имеет ненулевое
решение.
Теорема. Система линейных
уравнений имеет ненулевое решение,
если её определитель равен нулю.

7.

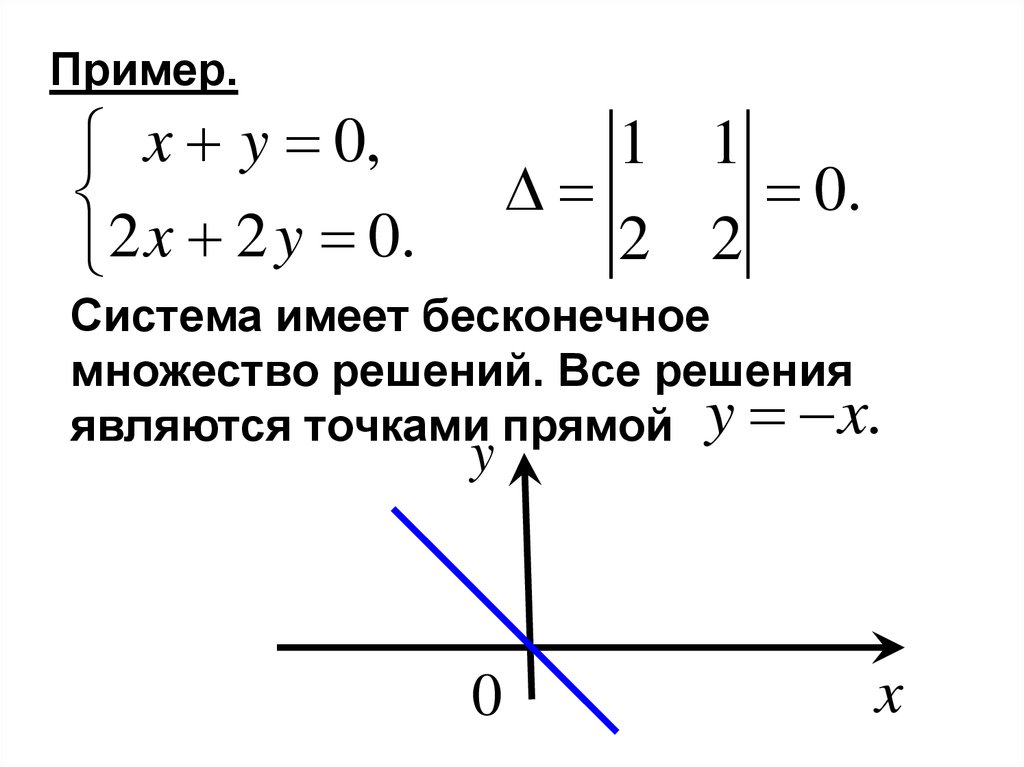
Пример.
x y 0,
2 x 2 y 0.
1 1
2 2
0.
Система имеет бесконечное
множество решений. Все решения
являются точками прямой y x.
y
0
x

8.

Вернемся к нашей системе. Составим
определитель системы
a11
a12
a21
a22
0,
или
a11 a22 a12 a21 0.
Получилось квадратное уравнение.
Такое уравнение называется
характеристическим. Корни
уравнения – это собственные
значения матрицы A.

9.

Примеры.
1. Найти собственные значения
матрицы
1 3
A
.
1 5
Запишем матрицу
3
1
A E
.
1 5

10.

A E 0;
1
3
0.
1 5
(1 )(5 ) 3 0 или
2
6 8 0.
Находим корни характеристического
уравнения 1 2; 2 4.
Мы нашли собственные значения.
Ответ:
1 2; 2 4.

11.

Нахождение собственных векторов
1 3
2;
4.
A
.
1
2
1 5
1. Найдем собственный вектор,
соответствующий собственному
значению 2.
1
Рассмотрим уравнение
вместо подставим
Ax x
2.
и

12.

Тогда получим
Ax 2 x или
1 3 x1 2 x1
1 5 x 2 x
2 2
x1 3x2 2 x1
.
x1 5 x2 2 x2

13.

x1 3x2 2 x1 ,
x1 5 x2 2 x2 .
x1 3 x2 ,
x1 3 x2 .
Положим
x2 1,
Получилось
Отсюда
тогда
3
x .
1
x1 3.

14.

Можно считать, что мы нашли
собственный вектор. Но обычно этот
вектор нормируют, т.е. приводят его к
вектору единичной длины. Для этого
найдем длину вектора
x 3 1 10
2
и каждую координату разделим на
10.

15.

Получим
e1
3
10
.
1
10
- собственный вектор,
соответствующий собственному
значению 1 2.
e1

16.

Аналогично найдем e2 , т.е.
собственный вектор, соответствующий
2 4.
1 3 x1 4 x1
1 5 x 4 x ,
2 2
3 x2 3 x1 ,
x1 3x2 4 x1 ,
x2 x1.
x1 5 x2 4 x2 .

17.

x1 1,
1
x .
1
Пусть
тогда
x2 1.
Нормируем, т.е. разделим на
Получим
e2
1
2
.
1
2
x 2.

18.

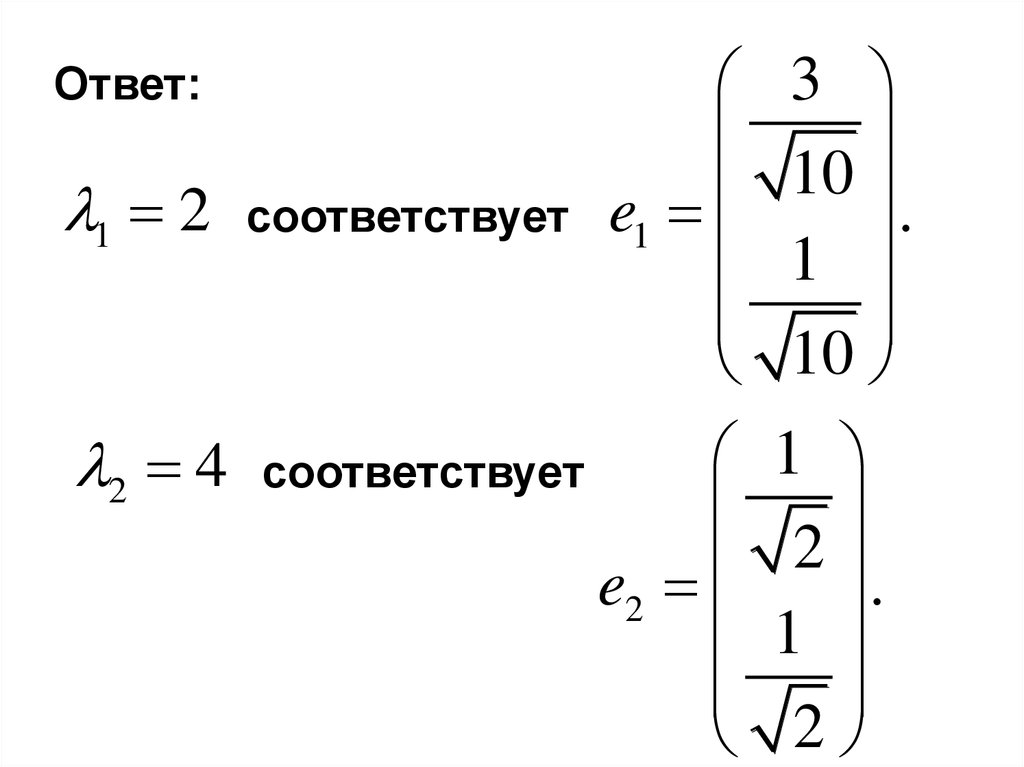
Ответ:
1 2
2 4
соответствует
соответствует
e1
e2
3
10
.
1
10
1
2
.
1
2

19.

Функция. Предел функции в точке.
Односторонние пределы. Пределы на
бесконечности. Непрерывность функции.
Точки разрыва функции и их
классификация.

20.

1. Предел в точке.
Рассмотрим пример.
Построить график функции
x 1,
x 1 x 1,
y
x 1 не сущ., x 1.
2

21.

y
M (1, 2)
2
0
1
Формула теряет смысл при
x
x0 1.

22.

В этом случае пишут:
y ( x) 2
при
x 1.
По-другому:
lim y( x) 2.
x 1

23.

Способы вычисления предела
1. Предел дроби при x :
деление на старшую степень.
0
1
2
2
2
1 2x
x
lim
lim
2.
2
x 2
x 2 x
1
2
x
0
Пример.

24.

2. Разложение на множители, когда
x
Пример.
x 1
x 1) 2.
lim
lim(
x 1
x 1 x 1
2

25.

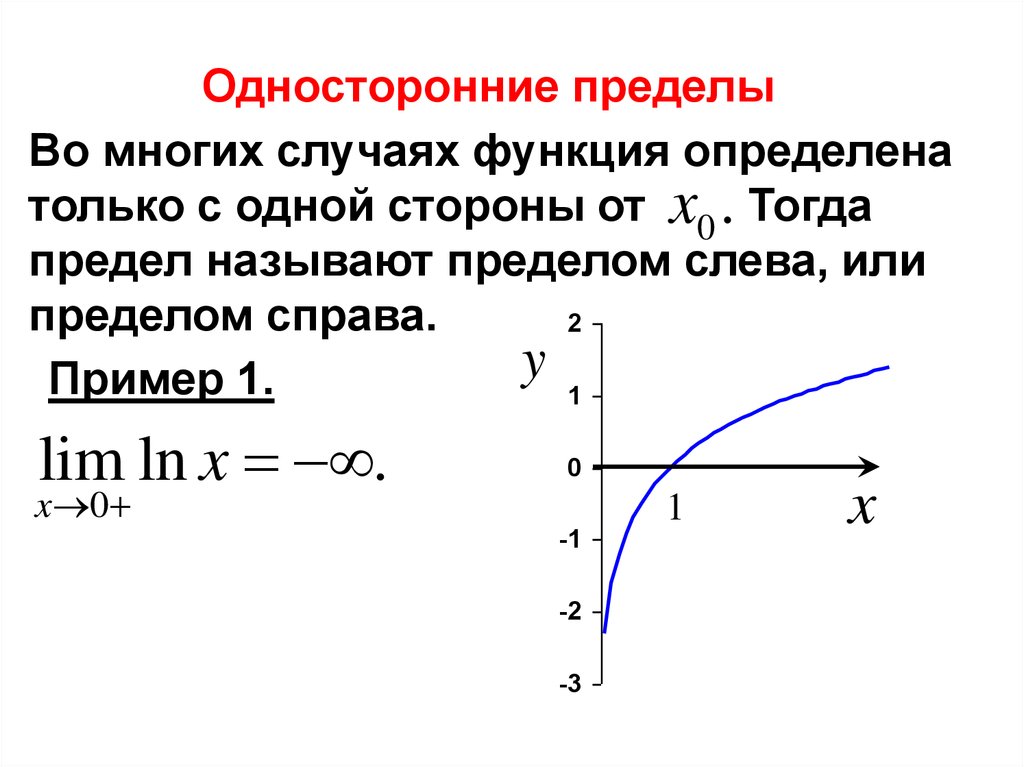
Односторонние пределы
Во многих случаях функция определена
только с одной стороны от x0 . Тогда
предел называют пределом слева, или
пределом справа.
2
y1
Пример 1.
lim ln x .
x 0
0
-1
-2
-3
1
x

26.

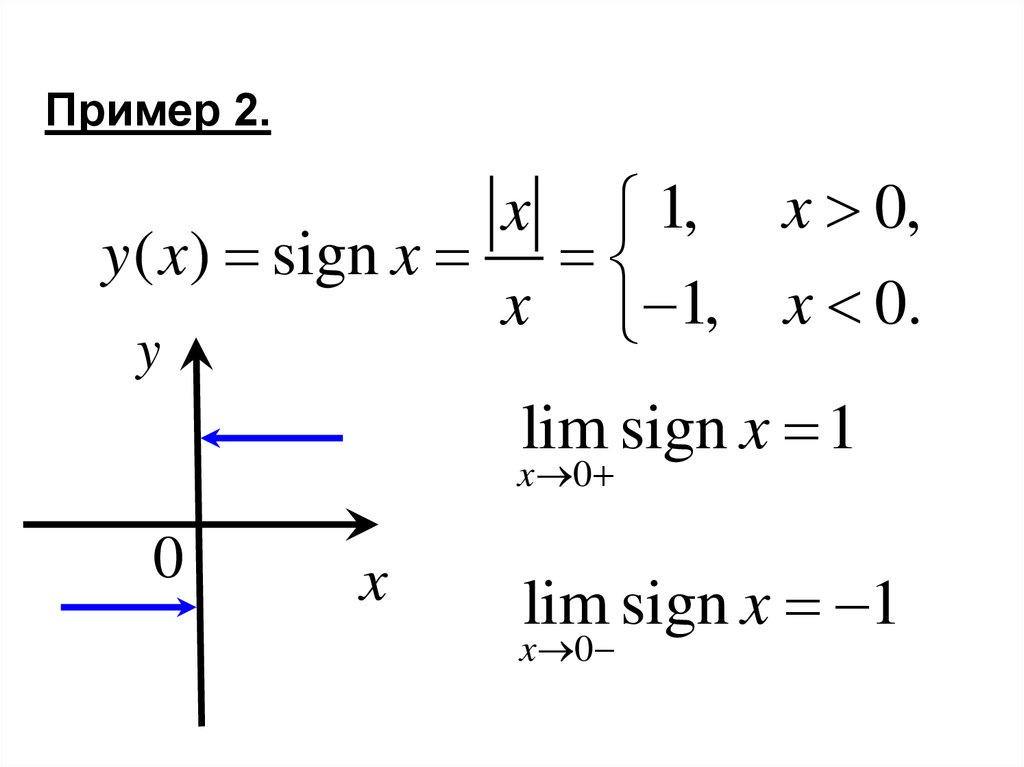
Пример 2.
x 1, x 0,
y ( x) sign x
x 1, x 0.
y
lim sign x 1
x 0
0
x
lim sign x 1
x 0

27.

Опр. Функция y y ( x) называется
непрерывной в точке x0 , если
lim y( x) y( x0 ).
x x0
Все элементарные функции
непрерывны на своей области
определения.
Пример. y x , y e
- непрерывные функции.
2
x
,
y sin x

28.

Опр. Если в точке x0 функция не
является непрерывной, то x0 - точка
разрыва.
Рассматриваются точки разрыва 1-го
и 2-ого рода.

29.

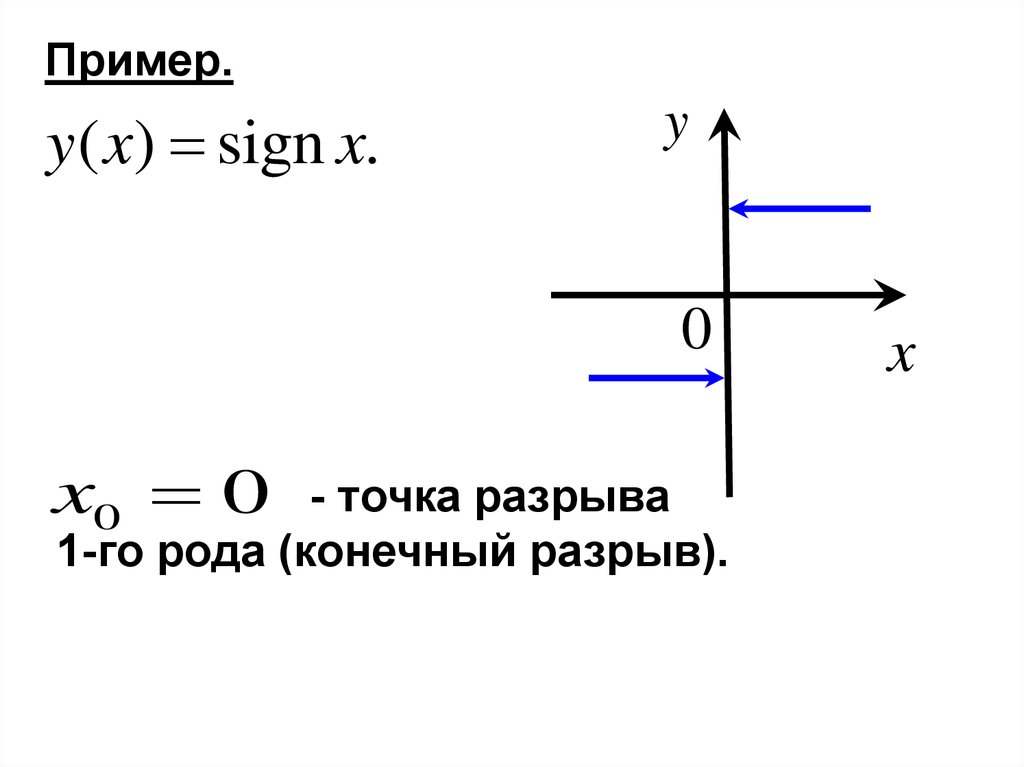
Пример.
y( x) sign x.
y
0
x0 0
- точка разрыва
1-го рода (конечный разрыв).
x

30.

Пример.
1
y ( x) .
x
x0 0
y
- точка
разрыва 2-ого рода
(бесконечный разрыв).
1
lim ;
x 0 x
0
1
lim .
x 0 x
x