Лекция 5. Случайные процессы

1. Лекция 5

Случайные процессы.

2. Содержание

• Особенности моделирования случайных
процессов.
• События. Случайные величины.
• Случайные процессы.
• Моделирование случайных процессов.

3. Объекты моделирования

Дискретные
Непрерывные
Детерминированные
• Число состояний
системы конечно.
• Переходы строго
определены
• Число состояний
бесконечно
• Динамика параметров
строго определена
Стохастические
• Число состояний
системы конечно
• Переходы определены
некоторым случайным
законом
• Число состояний
бесконечно
• Динамика параметров
задается случайными
функциями
Вычислительная система – это дискретный детерминированный
объект.
При моделировании решается задача описания любого
объекта дискретной детерминированной
схемой.

4.

Основные вопросы
• Дискретизация непрерывной задачи
• Сходимость = аппроксимация + устойчивость
• Оптимизация алгоритма
• Описание стохастической задачи как
детерминированной
• Как вообще вычленить закономерности в
«случайной» ситуации?
• Адекватность: когда и почему решение
детерминированной задачи «полезно» для
решения стохастической.

5. Содержание

• Особенности моделирования случайных
процессов.
• События. Случайные величины.
• Случайные процессы.
• Моделирование случайных процессов.

6. Некоторые определения

7. Некоторые определения

P( A ) 1
i
полная группа
P( Ai Aj ) 0 i j
P( Ai Aj ) P( Ai ) P( Aj ) i j

8. Некоторые определения

X : x1 , x2 ,
xn
в случае полной группы несовместных событий

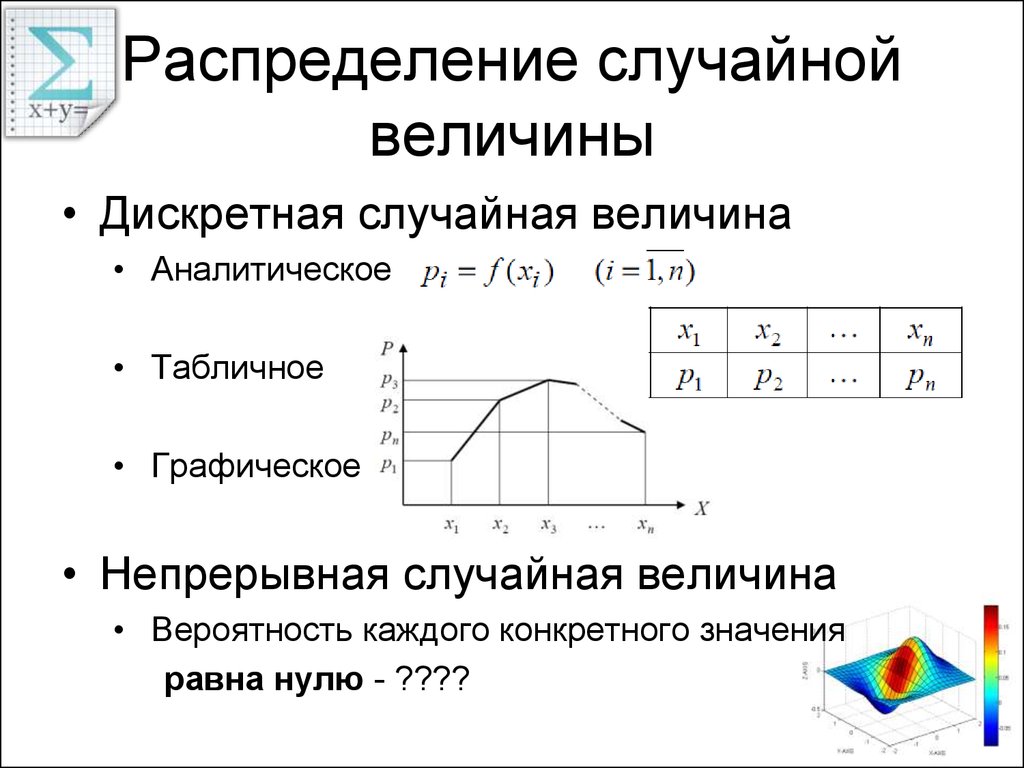
9. Распределение случайной величины

• Дискретная случайная величина
• Аналитическое
• Табличное
• Графическое
• Непрерывная случайная величина
• Вероятность каждого конкретного значения
равна нулю - ????

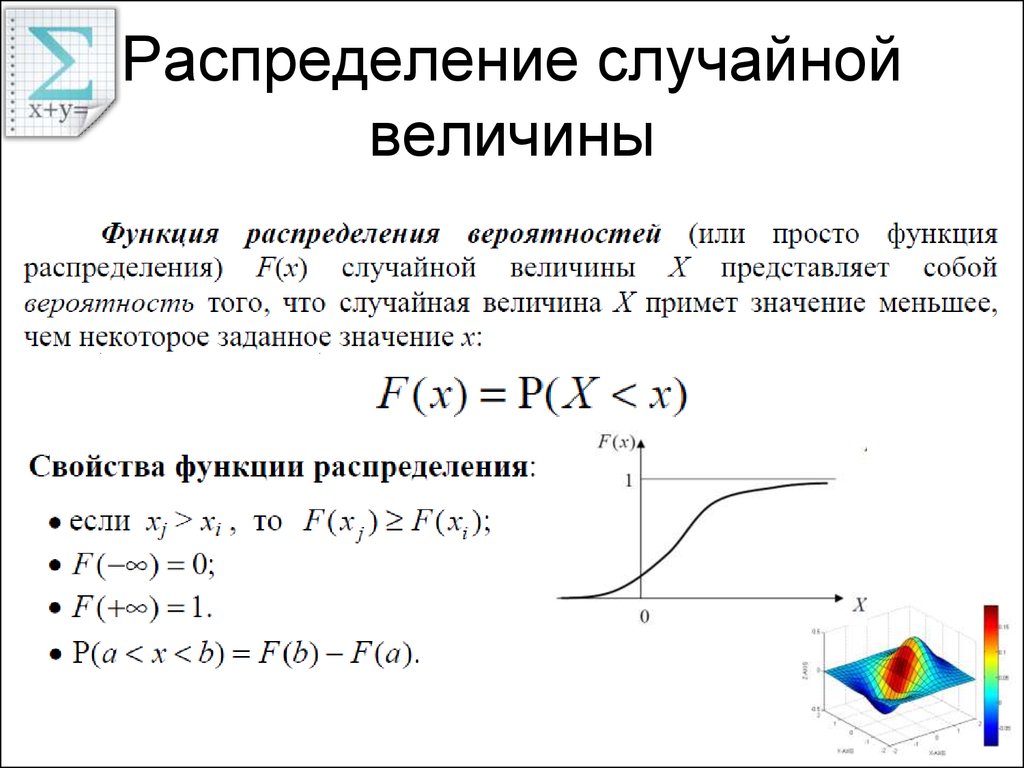
10. Распределение случайной величины

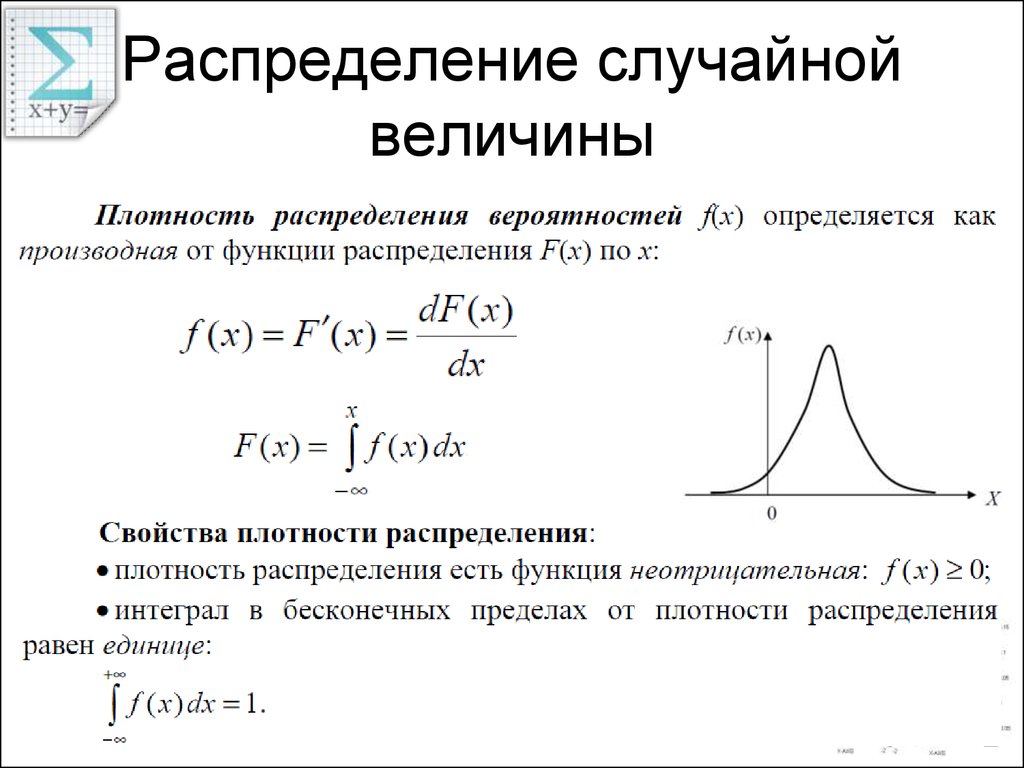
11. Распределение случайной величины

12. Моменты случайной величины

• В
Математическое ожидание

13. Моменты случайной величины

• Математическое ожидание – средневзвешенное
значение случайной величины
• Дисперсия – разброс значений случайной величины
относительно математического ожидания
• Среднеквадратичное отклонение
• Коэффициент вариации

14. Типовые распределения

• Распределение Пуассона
• Геометрическое распределение

15. Типовые распределения

• Равномерное распределение
• Экспоненциальное
распределение
• Распределение Эрланга

16. Содержание

• Особенности моделирования случайных
процессов.
• События. Случайные величины.
• Случайные процессы.
• Моделирование случайных процессов.

17. Случайный процесс

18. Случайный процесс

19. Случайный процесс

20. Марковские процессы

21. Марковские процессы

22. Марковские процессы

23. Процессы с непрерывным временем

24. Дифференциальная матрица

25. Вектор состояний системы

• Состояния системы:
• Вероятности нахождения системы в состоянии:
• Нормировочное условие:
• Стохастический вектор состояний системы:

26. Эргодические процессы

27. Эргодические процессы

28. Эргодические процессы

29. Эргодические процессы

30. Марковские процессы с дискретным временем

Система линейных алгебраических уравнений для расчёта
стационарных вероятностей состояний марковского процесса, которая
обладает единственным решением, если Q – эргодическая матрица.

31. Марковские процессы с непрерывным временем

32. Содержание

• Особенности моделирования случайных
процессов.
• События. Случайные величины.
• Случайные процессы.
• Моделирование случайных процессов.

33. Моделирование марковских процессов

34. Моделирование марковских процессов

35. Моделирование марковских процессов

36. Моделирование марковских процессов