Производная и её геометрический смысл. Производная в ЕГЭ!

1. Урок повторения по теме: Производная и её геометрический смысл. Производная в ЕГЭ!

2. Типы задач ЕГЭ :

1. Нахождение значения производной
функции в точке(геометрический смысл
производной).
2. Нахождение точек, в которых производная
функции равна 0.
3. Нахождение промежутков возрастания и
убывания функции.
4. Нахождение наибольшего и наименьшего
значения функции.

3. Геометрический смысл производной

Производная функции в точке
x0 равна
угловому коэффициенту
касательной к графику
функции y = f(x) в этой точке.
Т.е.
.
f ( x0 ) tg
'
Причем, если :
1. f ( x0 ) tg 0, то острый
'
2. f ' ( x0 ) tg 0, то развернутый
3. f ' ( x0 ) tg 0, то тупой

4.

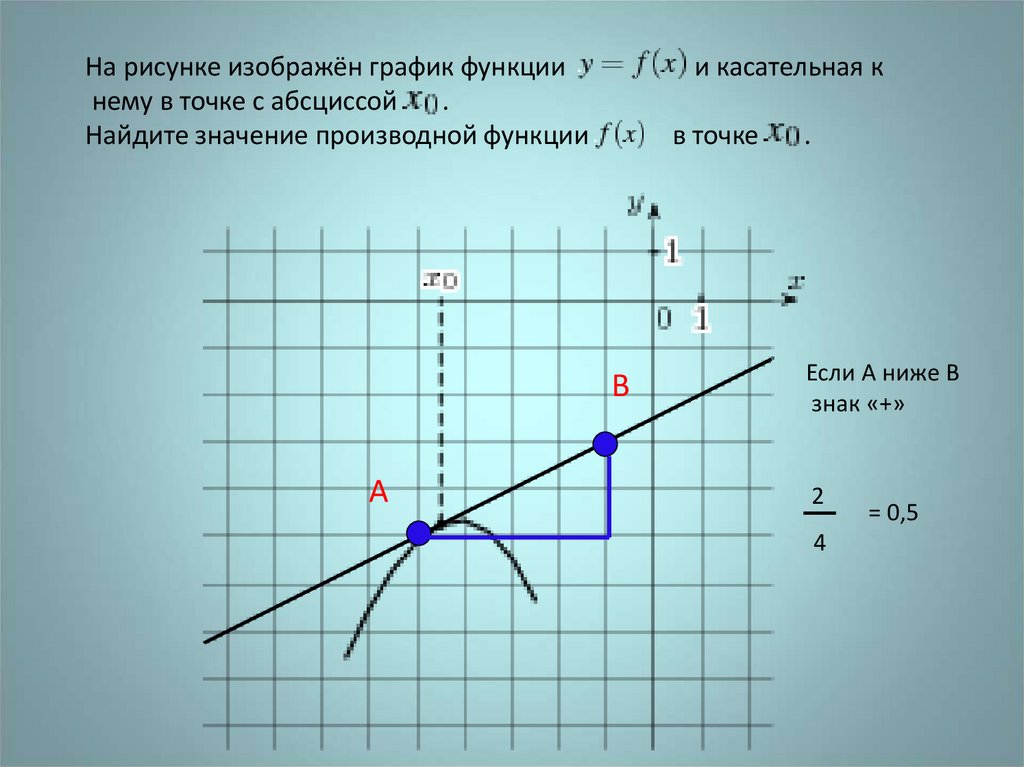
На рисунке изображён график функции
нему в точке с абсциссой
.
Найдите значение производной функции
и касательная к
в точке
В
А
.
Если А ниже В
знак «+»
2
4
= 0,5

5.

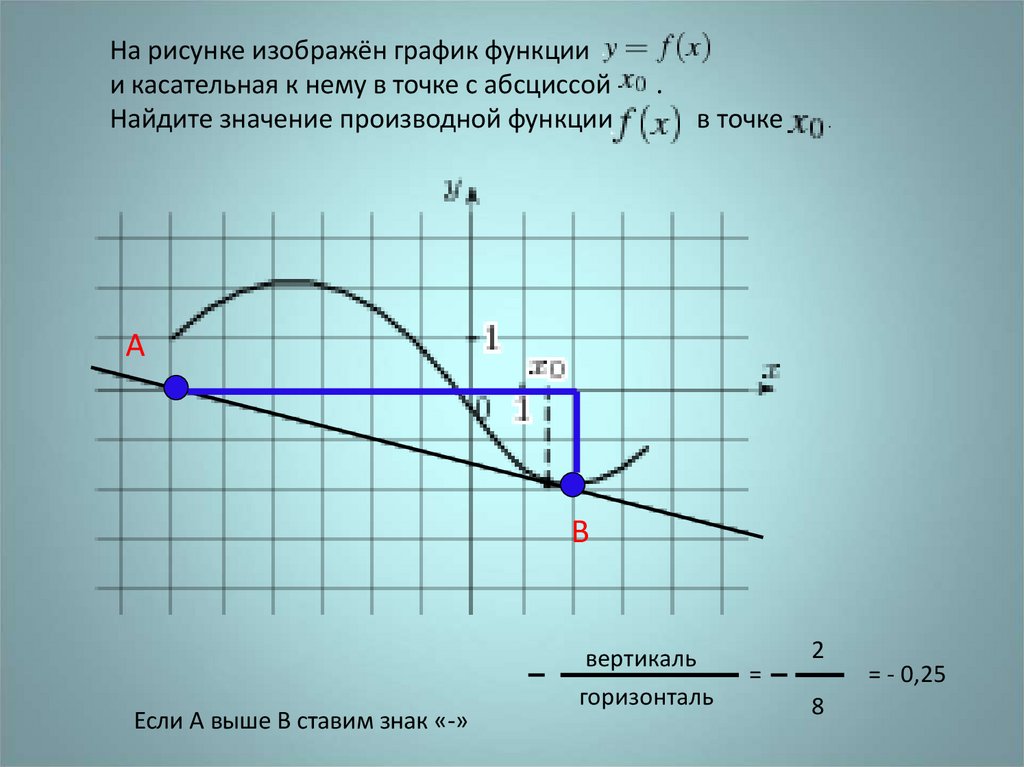
На рисунке изображён график функции
и касательная к нему в точке с абсциссой
Найдите значение производной функции
.
в точке
.
А
В
Если А выше В ставим знак «-»
вертикаль
горизонталь
=
2
8
= - 0,25

6.

На рисунке изображены график функции у =f(x) и касательная к этому
графику, проведенная в точке с абсциссой х0. Найдите значение
производной функции у =f(x) в точке х0.
у
Решение:
f‘(х0)=tga = 123
3
12
O
1
х
х0
у =f(x)
Ответ: 0,25

7.

На рисунке изображены график функции у =f(x) и касательная к этому
графику, проведенная в точке с абсциссой х0. Найдите значение
производной функции у =f(x) в точке х0.
Решение:
у
у =f(x)
f ( x0 ) k tg
tga
4
=
1
tga = 4
f '(x0) = - tgα= - 4
х0
х
1
O
-3
-7
Ответ: -4

8.

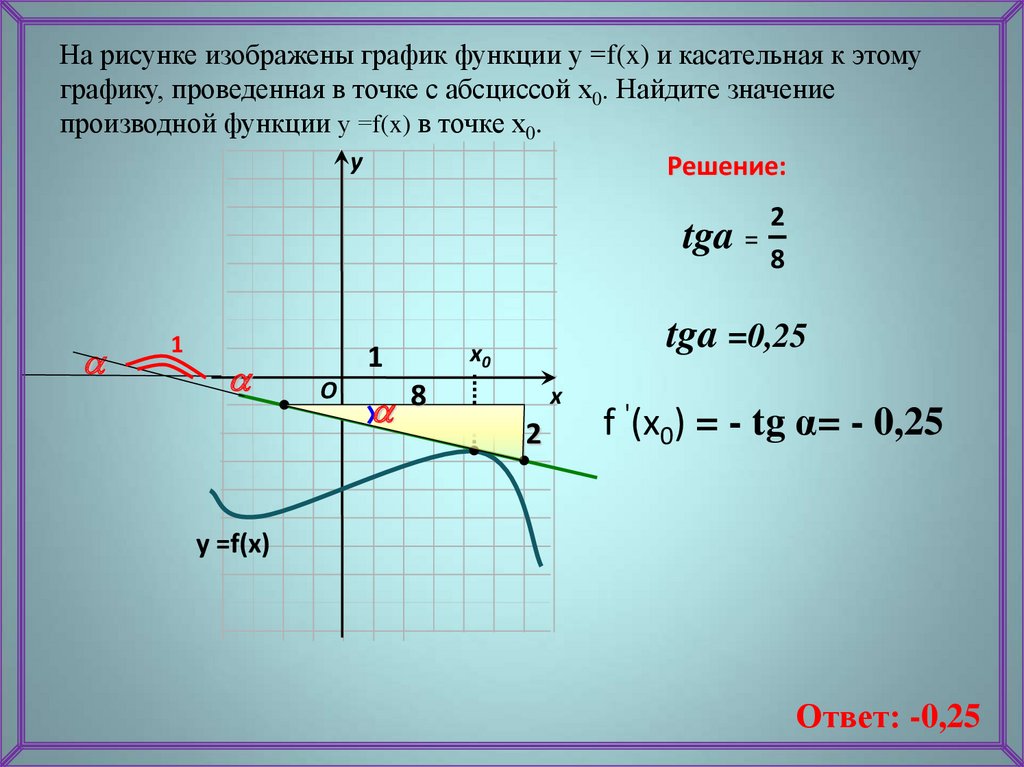
На рисунке изображены график функции у =f(x) и касательная к этому
графику, проведенная в точке с абсциссой х0. Найдите значение
производной функции у =f(x) в точке х0.
у
Решение:
tga
1
1
O
8
2
=
8
tga =0,25
х0
х
2
f '(x0) = - tg α= - 0,25
у =f(x)
Ответ: -0,25

9.

№9.Найдите
промежуткиграфик
возрастания
функции
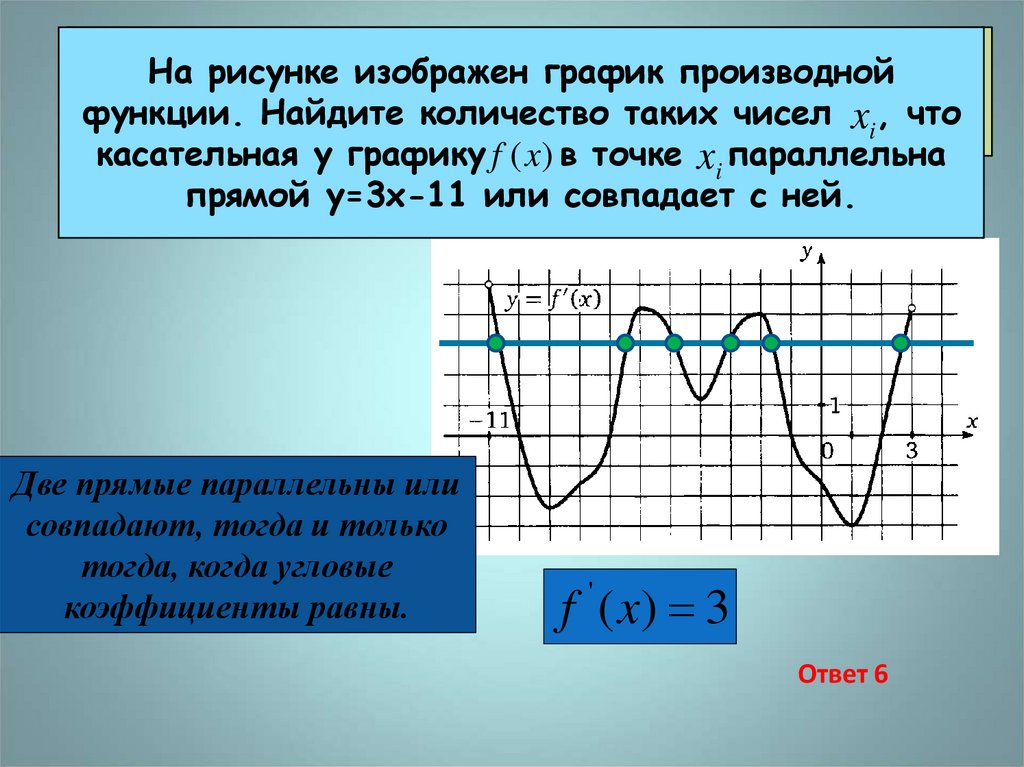
На рисунке изображен
производной
функции.
Найдите
количество
таких чисел
.В ответе
укажите
длину большего
из них
xi,. что
касательная у графику f (x ) в точке xi параллельна
прямой y=3x-11 или совпадает с ней.
Две прямые параллельны или
совпадают, тогда и только
тогда, когда угловые
коэффициенты равны.
f ( x) 3
'
Ответ 6

10.

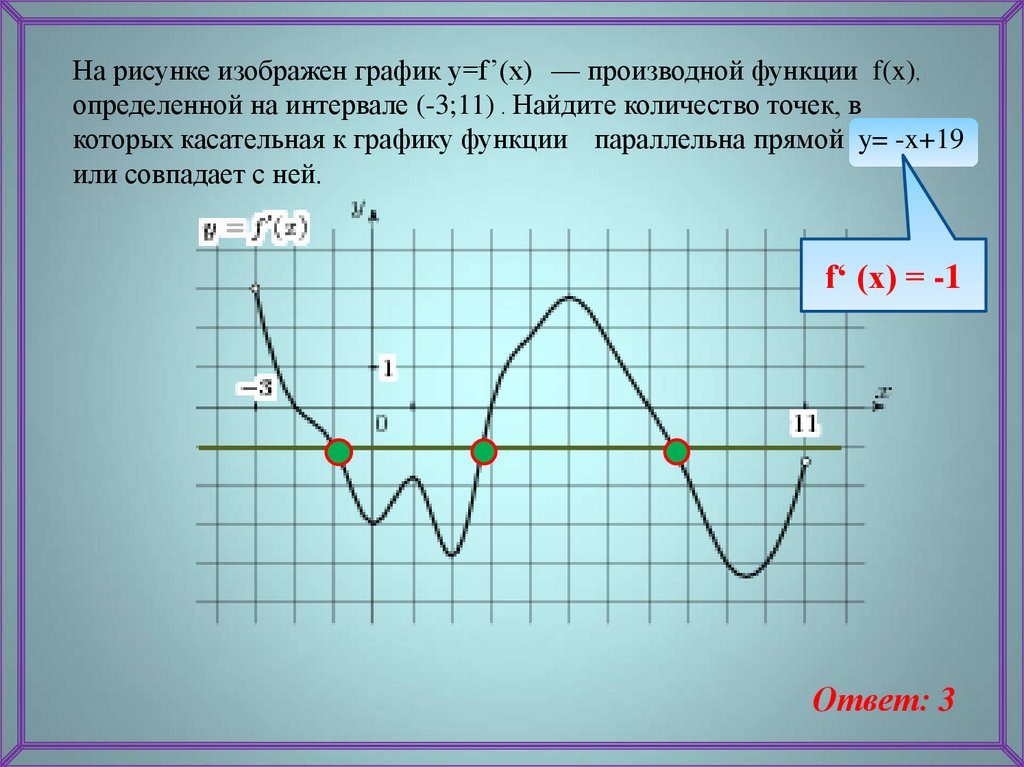
На рисунке изображен график y=f’(x) — производной функции f(x),
определенной на интервале (-3;11) . Найдите количество точек, в
которых касательная к графику функции параллельна прямой y= -x+19
или совпадает с ней.
f‘ (x) = -1
Ответ: 3

11.

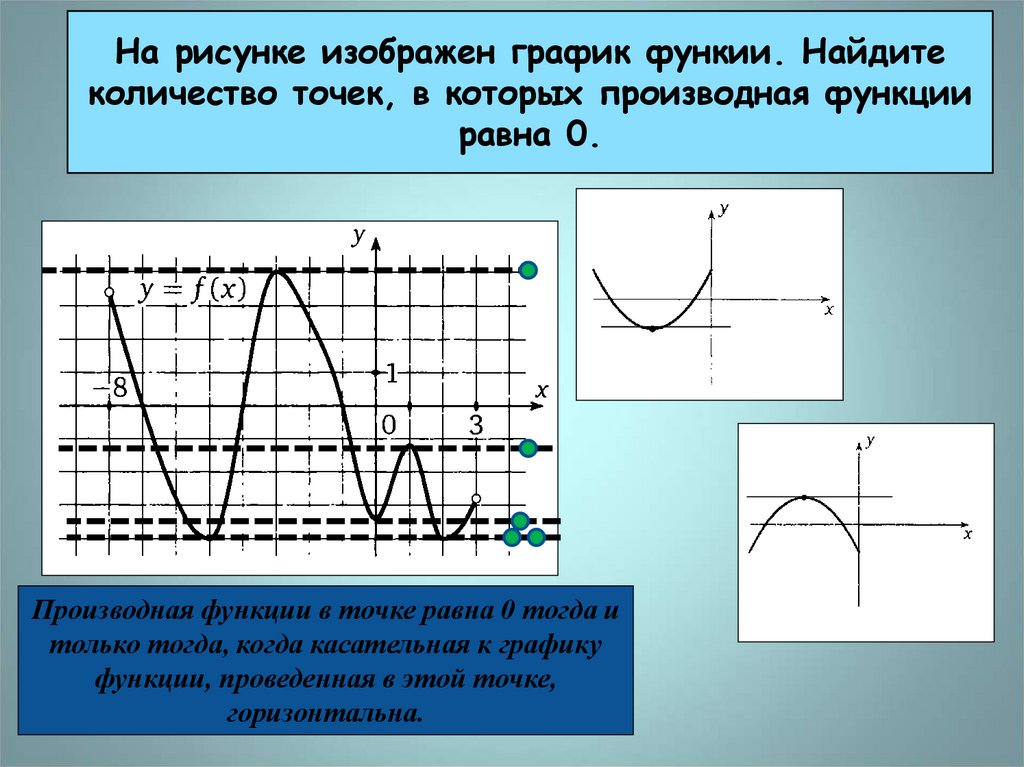
На рисунке изображен график функии. Найдите
количество точек, в которых производная функции
равна 0.
Производная функции в точке равна 0 тогда и
только тогда, когда касательная к графику
функции, проведенная в этой точке,
горизонтальна.