Похожие презентации:
Транспортная задача линейного программирования
1.
ТЕМА 3.Транспортные модели
обоснования решений
Лекция 5.
Транспортная задача
линейного программирования
2.
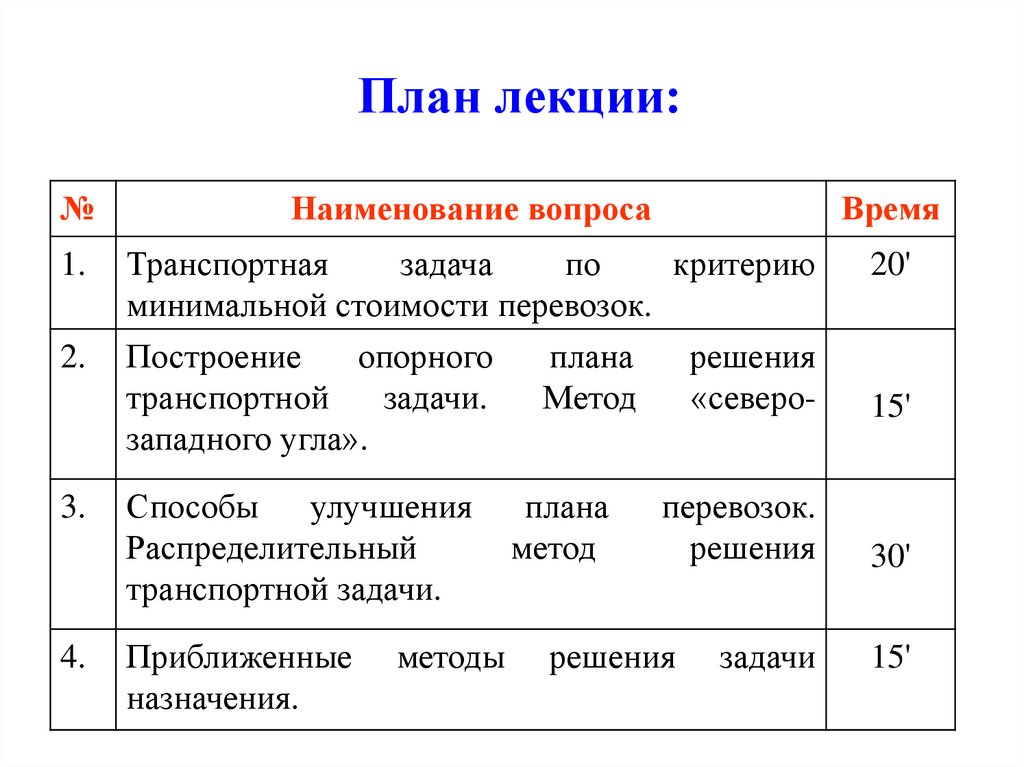
План лекции:№
Наименование вопроса
Время
1.
Транспортная
задача
по
критерию
минимальной стоимости перевозок.
Построение
опорного
плана
решения
транспортной
задачи.
Метод
«северозападного угла».
20'
2.
3.
4.
Способы
улучшения
Распределительный
транспортной задачи.
Приближенные
назначения.
методы
плана
метод
перевозок.
решения
решения
задачи
15'
30'
15'
3.
ЛИТЕРАТУРА1. Вентцель Е.С. Задачи, принципы, методология:
учеб. пособие для вузов / Вентцель Е.С. – Москва:
Дрофа, 2006. – 206 с. Стр. 71-80.
4.
ВведениеСуществуют частные типы задач линейного
программирования, которые, в силу особой своей
структуры, допускают решение более простыми
методами, чем классический.
Это так называемые транспортные задачи (ТЗ).
Различают два основных вида ТЗ:
1) ТЗ по критерию
перевозок;
минимальной
стоимости
2) ТЗ по критерию минимума времени перевозок.
5.
Вопрос 1Транспортная задача по критерию
минимальной стоимости перевозок
6. Классическая ТЗ ЛП формулируется следующим образом: 1. Имеется m пунктов отправления (ПО): А1, …, Аm, в которых сосредоточены
Классическая ТЗ ЛП формулируетсяследующим образом:
1. Имеется m пунктов отправления (ПО):
А1, …, Аm, в которых сосредоточены запасы
какого-то однородного груза в количестве
соответственно α1, α2, …, αm единиц груза.
2. Имеется n пунктов назначения (ПН):
В1, …, Вn, подавших заявки соответственно на
b1, …, bn единиц груза.
7.
Предполагается, что сумма всех заявокравна сумме всех запасов.
Это уравнение обозначим (1):
m
n
i 1
j 1
ai b j
8.
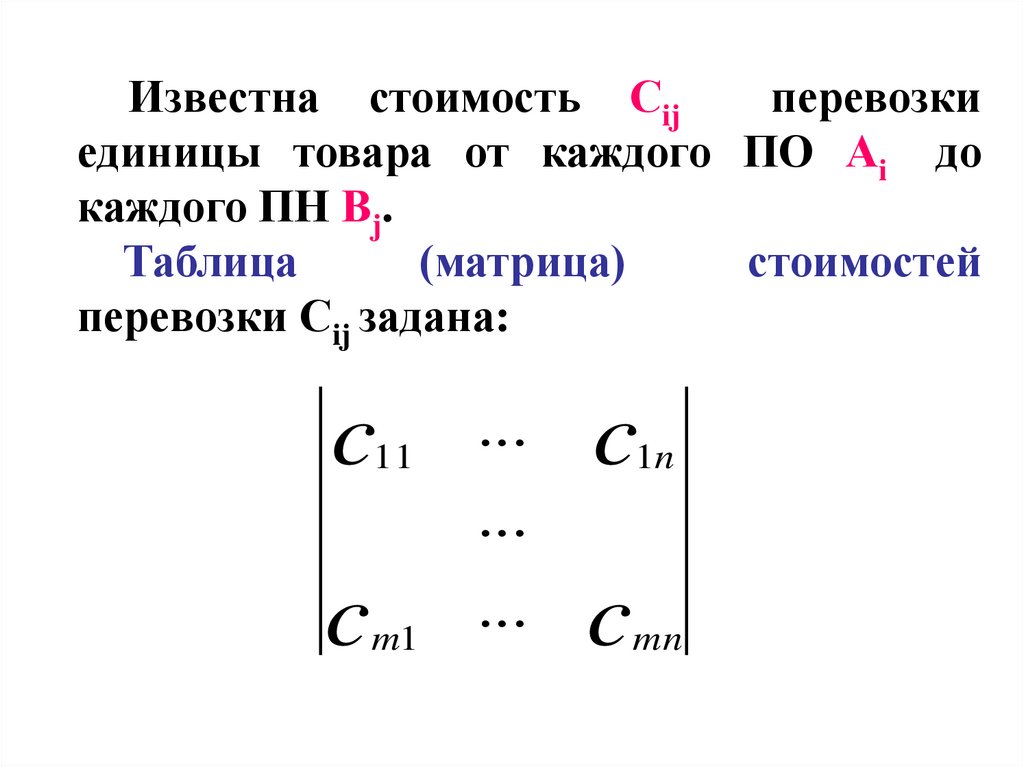
Известна стоимость Сijперевозки
единицы товара от каждого ПО Аi до
каждого ПН Вj.
Таблица
(матрица)
стоимостей
перевозки Сij задана:
c
11
c
m1
...
...
...
c
1n
c
mn
9.
Требуется составить такой план перевозок, прикотором:
1) все заявки будут выполнены,
2) общая стоимость всех перевозок будет
минимальна.
При такой постановке задачи показателем
эффективности плана перевозок будет являться
стоимость.
Поэтому поставленную задачу называют
транспортной задачей по критерию стоимости.
Дадим математическую формулировку этой
задачи.
10.
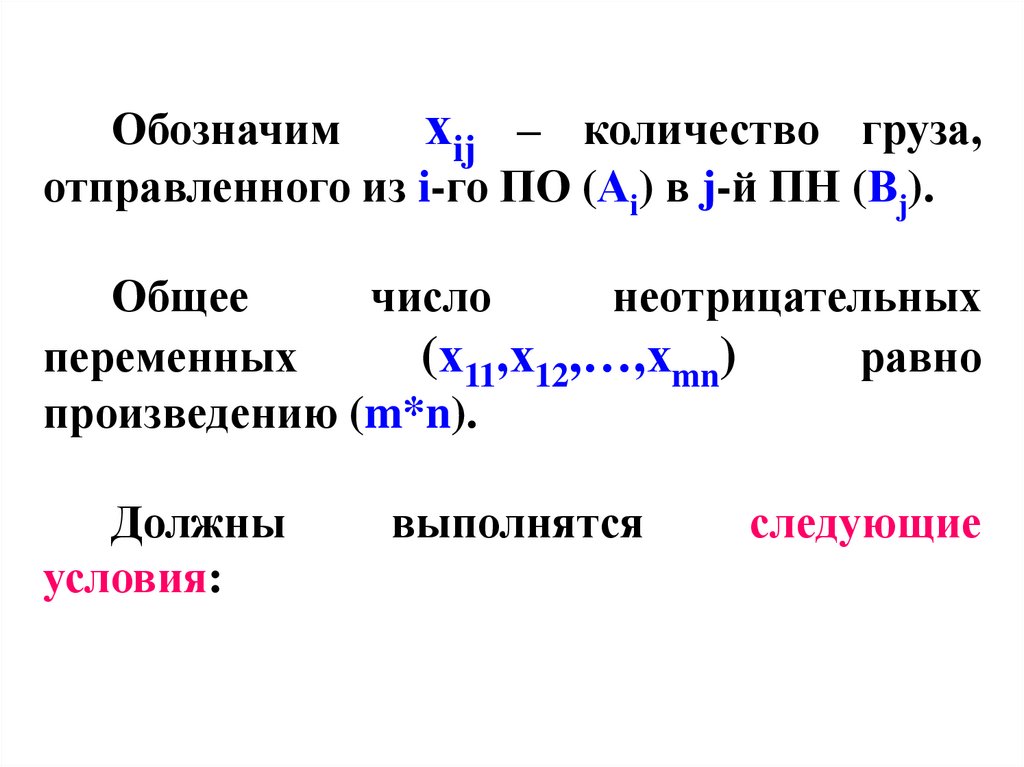
Обозначимхij – количество груза,
отправленного из i-го ПО (Аi) в j-й ПН (Вj).
Общее
число
неотрицательных
переменных
(х11,х12,…,хmn)
равно
произведению (m*n).
Должны
условия:
выполнятся
следующие
11.
Условие первое:Суммарное
количество
груза,
отправленное из каждого ПО во все ПН,
должно быть равно запасу груза в
данном пункте.
Это условие дает нам систему (2) из m
условий-равенств:
12.
x x ... xa1
11
12
1
n
...
x m 1 x m 2 ... x mn a m
или в коротком виде:
n
x1 j a1
j 1
...
n
x
am
mj
j 1
(2)
13.
Условие второе:Суммарное
количество
груза,
доставляемое в каждый ПН изо всех ПО,
должно быть равно заявке, поданной ПН.
Это условие дает ещё одну систему (3),
состоящую из n условий-равенств:
14.
x11 x21 ... xm1 b1x12 x22 ... xm 2 b2
...
x x ... x b
2n
mn
n
1n
или
xi1 b1
i 1
...
m
xin bn
i 1
m
(3)
15.
Условие третье:Суммарная стоимость всех перевозок, т.е.
сумма всех Хij, умноженных на соответствующие
стоимости Сij, должна быть минимальной:
L c 11 x 11 c 12 x 12 ...
c 1n x 1n c 21 x 21 c 22 x 22 ...
c 2 n x 2 n ... c mn x mn min
или короткая запись:
m
n
L cij xij min
(4)
i 1 j 1
Как видно, целевая функция
равенства являются линейными.
и ограничения-
16.
Таким образом, перед нами типичная задачалинейного программирования.
Ее можно решить симплекс-методом, но
данная задача имеет некоторые особенности,
позволяющие решить ее более простым способом.
Перечислим эти особенности:
1. Обратим внимание, что все коэффициенты
в системах уравнений (2) и (3) равны единице.
2. Складывая между собой все уравнения (2) и
(3) мы должны получить одно и то же, по условию
(1).
17.
Таким образом, условия (2) и (3) связаны однойлинейной зависимостью.
Тогда число линейно-зависимых уравнений
здесь: (m+n-1).
Это значит, что ранг системы уравнений (2) и (3)
равен r=m+n-1 и определяет число независимых,
базисных переменных, которые мы можем выразить
через свободные.
Число свободных переменных равно:
k mn ( m n 1)
mn m ( n 1)
m(n 1) (n 1)
(m 1)( n 1)
18.
В задаче ЛП оптимальное решениедостигается в одной из вершин области
допустимых решений, где, по крайней мере,
k переменных обращается в нуль.
Это значит, что в нашем случае для
оптимального плана перевозок, по крайней
мере k=(m-1)(n-1) значений Хij будет равно
нулю.
19.
Введем ряд определений.Значения Хij количества единиц груза,
направленных из Аi в Вj будем называть
перевозками.
Любая совокупность значений (Хij) –
планом перевозок или просто планом.
План (Хij) называется допустимым,
если он удовлетворяет условиям (2), (3), т.е.
все заявки удовлетворены, все запасы
исчерпаны.
20.
Решение транспортной задачи существуетвсегда.
Допустимый план будем называть опорным,
если в нем отличны от нуля не более r=m+n-1
базисных перевозок Хij, а остальные (перевозки)
равны нулю.
План (Хij) – оптимальный, если среди всех
допустимых планов, он имеет наименьшую
стоимость всех перевозок.
Методы решения сводятся к операциям с
транспортной таблицей, где в определенном
порядке записаны все условия транспортной
задачи.
21.
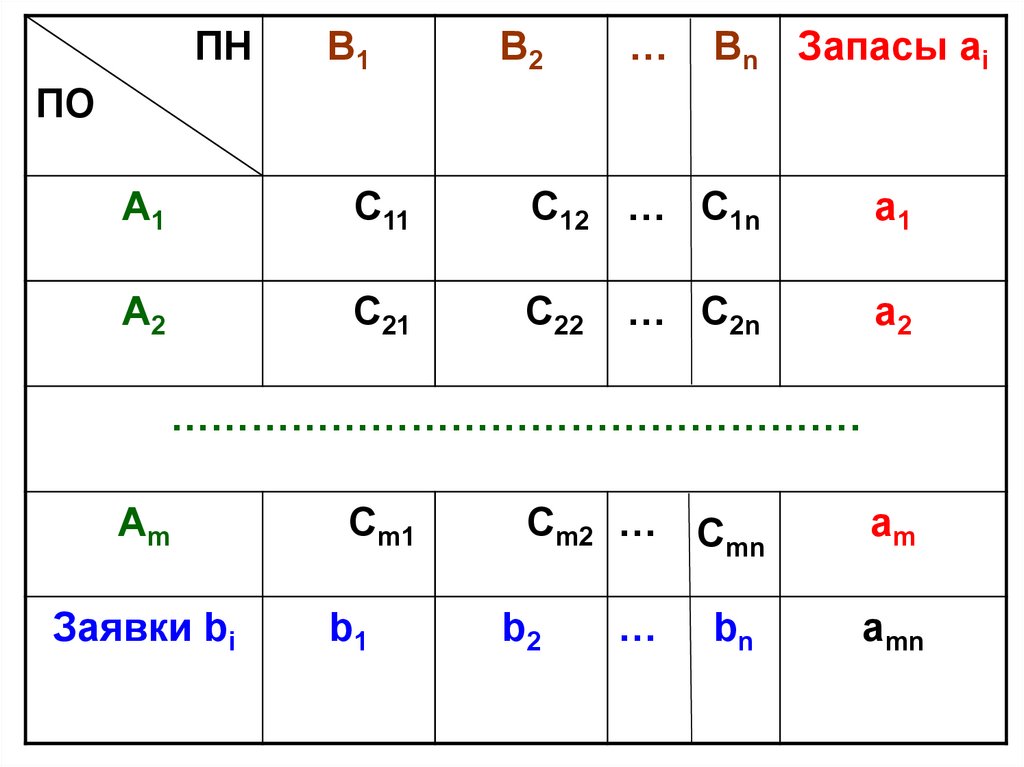
В транспортной таблице записываются:1) ПО и ПН;
2) запасы и заявки;
3) стоимость перевозок – в правом верхнем
углу клеток.
Ячейки (клетки) таблицы, в которых будем
записывать перевозки, называются базисными,
а остальные (пустые) – свободными.
22.
ПНВ1
В2
…
Вn Запасы ai
ПО
A1
C11
C12 … C1n
a1
A2
C21
C22
… C2n
a2
…………………………………………….
Am
Заявки bi
Cm1
Cm2 … C
mn
am
b1
b2
…
amn
bn
23.
Вопрос 2.Построение опорного решения
транспортной задачи.
Метод «северо-западного угла».
24.
Решение транспортной задачи начинается, как идля всякой задачи ЛП, с нахождения опорного плана.
Построение опорного плана методом «северозападного угла» поясним на конкретном примере.
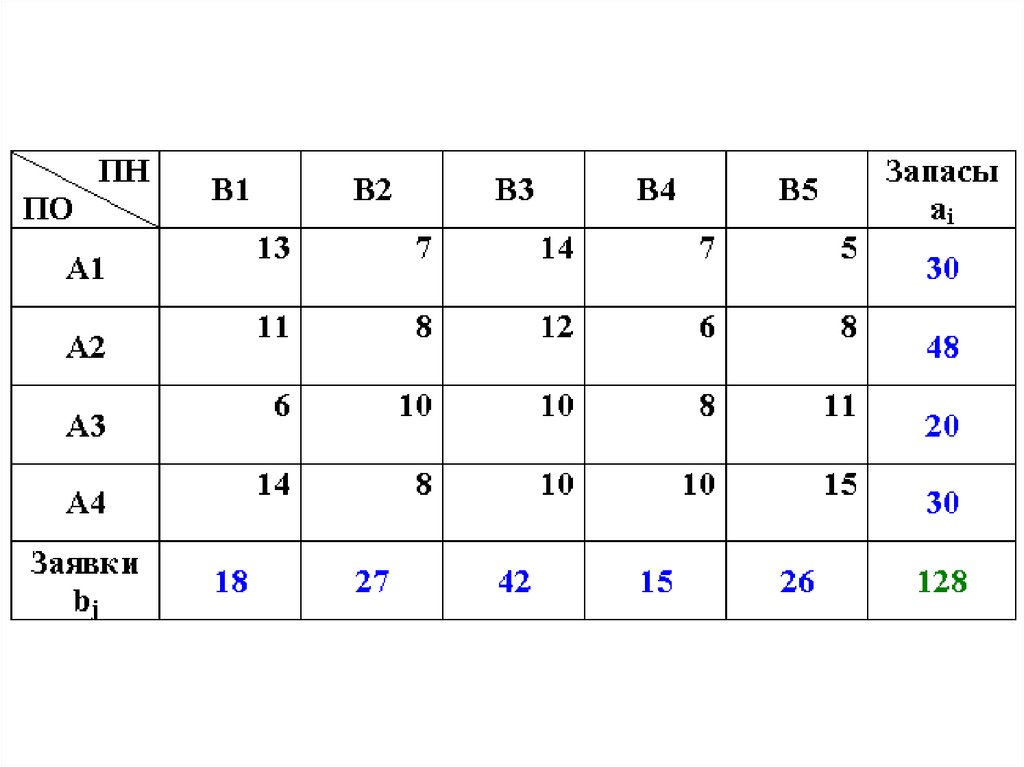
Пример.
Из 4-х складов (m=4) необходимо доставить по
заявкам в 5 магазинов 128 единиц крупногабаритного
товара (например, холодильников). Заявки из ПН и
запасы в ПО записаны в таблице
Начнем заполнение таблицы с левого верхнего
угла, т.е. с северо-западного угла.
25.
26.
27.
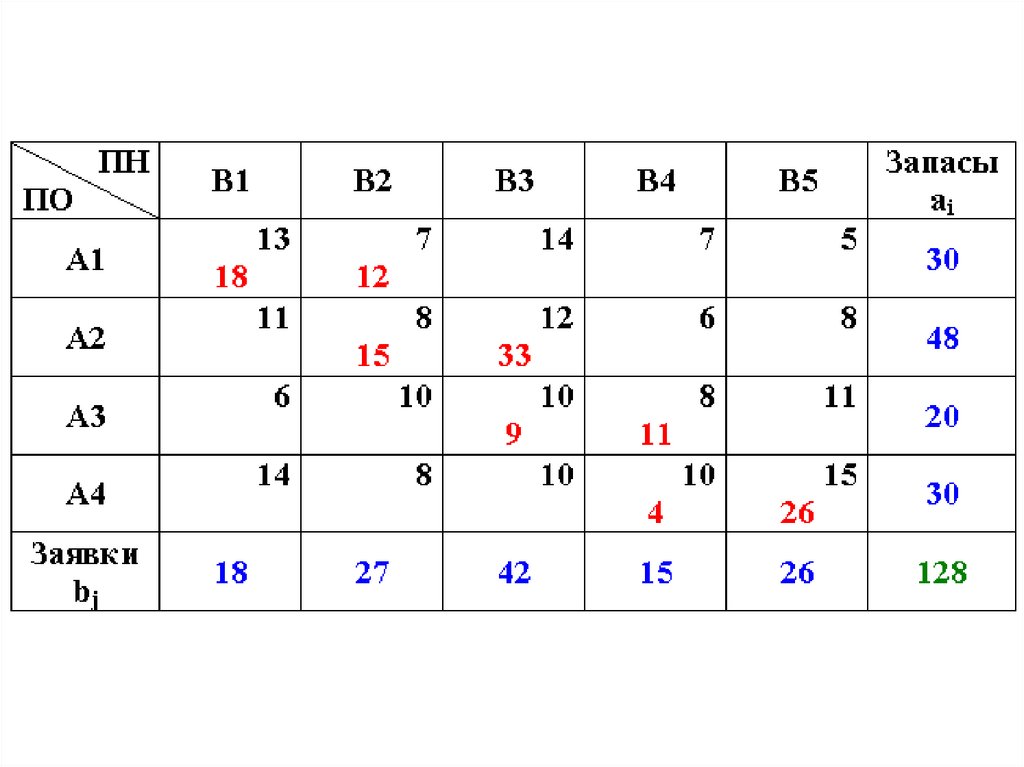
Полученный план – допустимый?Да. Все заявки – удовлетворены, все
запасы – исчерпаны.
Полученный план – опорный?
Да. r = m+n-1 = 4+5-1 = 8 базисных
клеток заполнено.
Число свободных клеток
k = (m-1)(n-1)=3*4=12
Оптимальный?
Оценим общую стоимость перевозок.
L = 18*13 + 12*7 + 15*8 + 33*12 + 9*10 +
+ 4*10 + 26*15 = 1442 (условные
денежные единицы).
28.
Вопрос 3.Способы улучшения плана
перевозок.
Распределительный метод
решения ТЗ.
29.
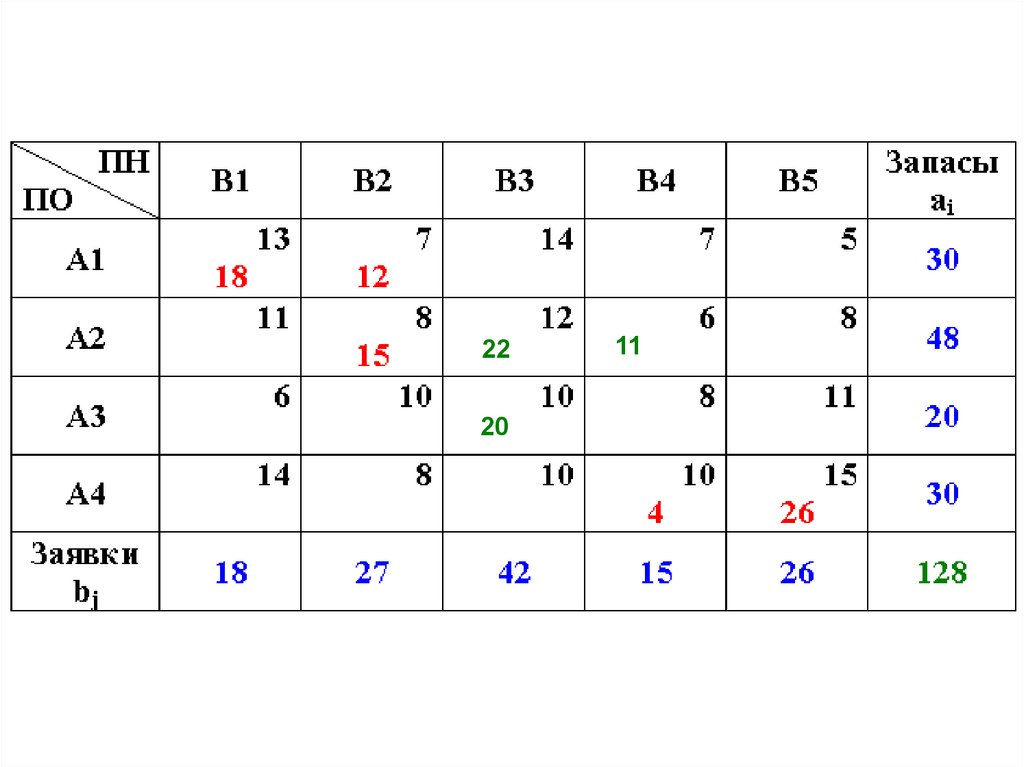
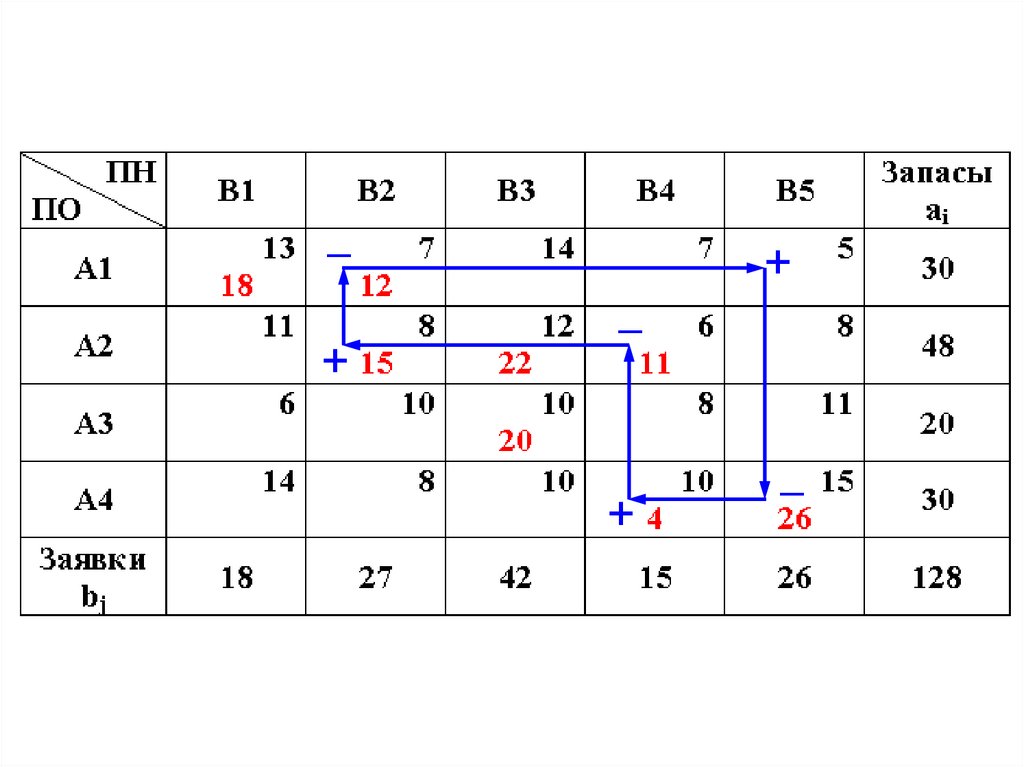
Продолжим решение примера.Можно улучшить опорный план, если
уменьшить перевозки в «дорогой» клетке
(2,3) со стоимостью С23=12, увеличив
перевозки в «дешевой» клетке (2,4) с
С24=6.
Чтобы план остался опорным мы
должны сделать одну из свободных
клеток базисной, а одну из базисных
свободной.
30.
Циклом в ТЗ будем называть несколькоклеток, замкнутых ломаной линией, которая в
каждой клетке совершает поворот на 900.
Каждый цикл имеет четное количество
вершин.
Условимся отмечать знаком «+» те вершины
цикла, в которых перевозки увеличиваются, а
знаком «-» те, в которых они уменьшаются.
Максимально
возможное
количество
груза, перемещаемое по циклу, определяется
минимальным грузом, расположенным в
отрицательных вершинах цикла.
В примере:
x min( x23 , x34) min( 33,11) 11
31.
Ценой цикла называется изменениестоимости перевозок, при перемещении одной
условной единицы груза по циклу.
Цена цикла равна алгебраической сумме
стоимостей, стоящих в вершинах цикла.
Причем
стоимости,
стоящие
в
положительных вершинах цикла берутся со
знаком «+», а стоимости отрицательных
вершин – со знаком «-». В данном случае
с24 с34 с33 с23 6 8 10 12 4
32.
–+
+
–
33.
2220
11
34.
Для улучшения плана имеет смыслперемещать перевозки по тем циклам, цена
которых отрицательна.
Тогда
выигрыш
при
реализации
перемещения груза по рассмотренному циклу
составит
L x ( 4) 11 44
(условные стоимостные единицы).
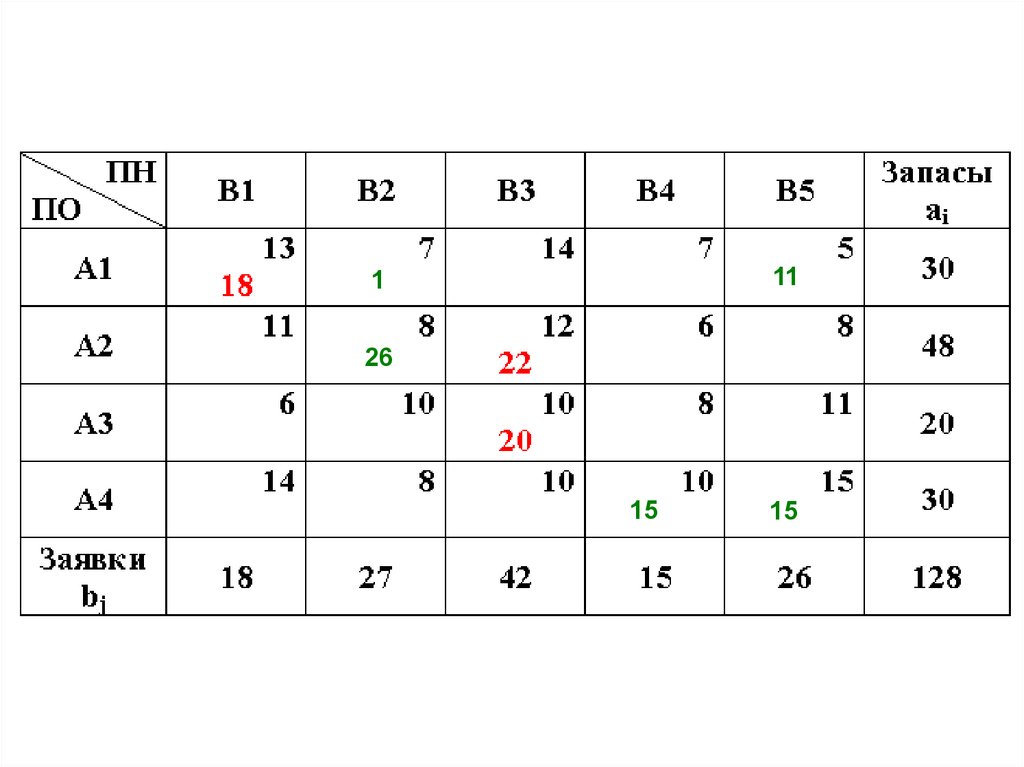
Попробуем еще улучшить план.
Для
этого
организуем
цикл
по
перемещению груза в «дешевую» клетку (1,5)
С15=5.
35.
–+
+
–
+
–
36.
111
26
15
15
37.
Цена цикла составит:с15 с45 с44 с24 с22 с12 5 15 10 6 8 7 5
Выигрыш составит:
L ( 5) 11 55
т.е. общая стоимость перевозок, уменьшится
еще на 55 единиц.
Если в ТЗ нельзя больше построить
циклов с отрицательной ценой, значит,
получен оптимальный план.
38.
Вывод.Сущность «распределительного метода»
решения транспортной задачи, заключается в
процессе
перераспределения
единиц
перевозимого груза в ячейки с меньшей
стоимостью с целью уменьшения общей
стоимости перевозок.
39.
Вопрос 4.Приближенные методы
решений задачи назначения
40.
На эффективность оптимизации большоезначение оказывает точность определения
элементов матрицы связей "цель – средство".
Иногда на практике нет возможности
определить эти элементы с достаточной
точностью, а точные методы оптимизаций
требуют выполнения большого объема
вычислительных
работ,
а
результат,
получаемый при этом, довольно приблизителен.
В
подобных
случаях
применяют
приближенные методы оптимизации.
41.
Метод максимума по строке.Заполнение таблицы назначений начинаем с
элемента первой строки, для которого C максимально
(если таких элементов несколько, то выбираем элемент
с наименьшим индексом).
Затем вычеркиваем первую строку и столбец,
который содержит максимальный элемент.
Далее рассматриваем вторую строку, находим
максимальный элемент и вычеркиваем вторую строку и
столбец, который содержит максимальный элемент.
Процедура повторяется до просмотра всех строк.
42.
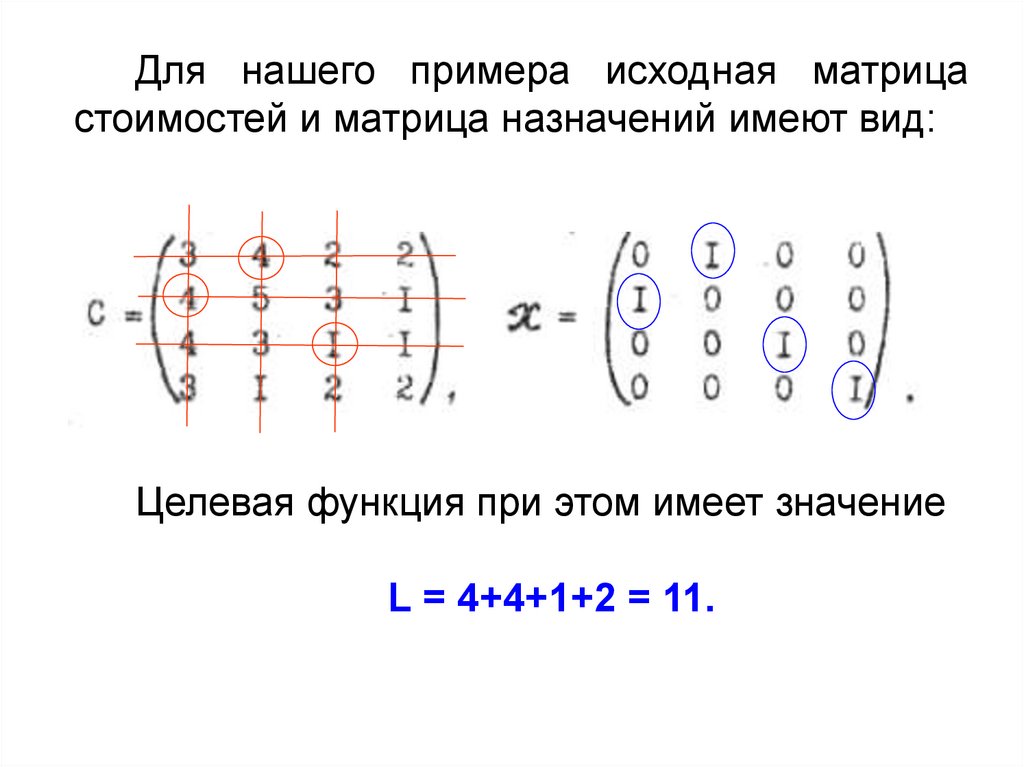
Для нашего примера исходная матрицастоимостей и матрица назначений имеют вид:
Целевая функция при этом имеет значение
L = 4+4+1+2 = 11.
43.
Метод максимума по столбцу.Процедура заполнения матрицы назначений
по этому методу организуется так же, как по
методу максимума по строке с той лишь
разницей, что анализируются столбцы. Для
нашего примера матрица назначений примет
вид
Целевая функция равна:
L = 4+4+2+1 = 11.
44.
Метод максимального элемента матрицы.Правило заполнения матрицы сводится к
выбору
максимального
элемента
и
вычеркивания этой строки и столбца, на
пересечении которых лежит максимальный
элемент.
Далее, из оставшихся невыделенных
элементов снова выбирается максимальный и
так до просмотра всей матрицы. При этом
матрица назначений примет вид:
Целевая функция
L = 5+4+2+2 = 13.
45.
Достоинствомрассмотренных
методов является их простота, которая
достигнута в ущерб точности решения
задачи назначения.
Эти
методы
могут
быть
использованы
для
получения
начальных опорных планов при
решении транспортной задачи методом
потенциалов.








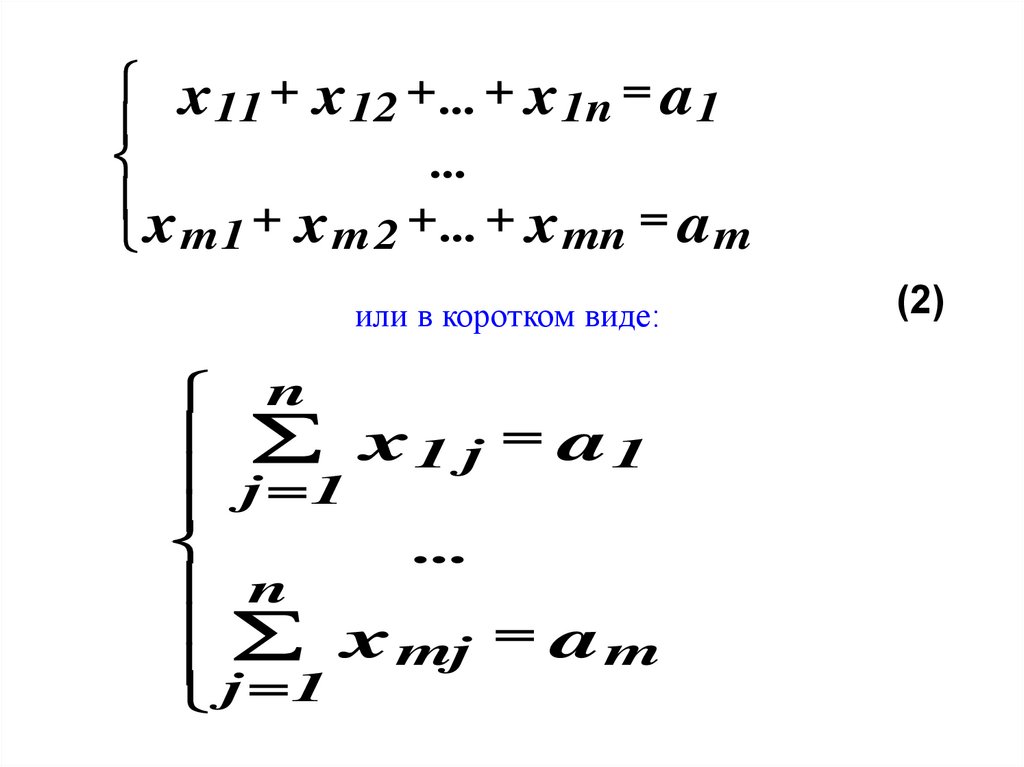


























 Математика
Математика








