Транспортная задача линейного программирования (ЛП)

1.

Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ижевский государственный технический университет
имени М. Т. Калашникова»
Кафедра «АСОИУ»
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного
программирования (ЛП)»
Автор Исенбаева Е.Н., старший преподаватель
Ижевск
2014

2. ПОСТАНОВКА Т- задачи.

Пусть в пунктах производства A1, A2 ,…, Am производят
некоторый однородный продукт, причем объем производства в
пункте Ai составляет аi, единиц i = 1, 2,…, m.
Допустим, что данный продукт потребляют в пунктах
потребления В1, В2 ,…, Вn , а объем потребления в пункте Bj
составляет bj единиц j =1, 2, .., …, n.
Предположим, что из каждого пункта производства возможна
транспортировка продукта в любой пункт потребления.
Транспортные издержки по перевозке из пункта Ai в пункт Bj
единицы продукции равны cij (i = 1, 2, ..., m; j=1, 2, ..., n).
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
2

3. Решение задачи

Задача состоит в определении такого плана перевозок,
при котором запросы всех потребителей полностью
удовлетворены, весь продукт из пунктов производства
вывезен и суммарные транспортные издержки
минимальными.
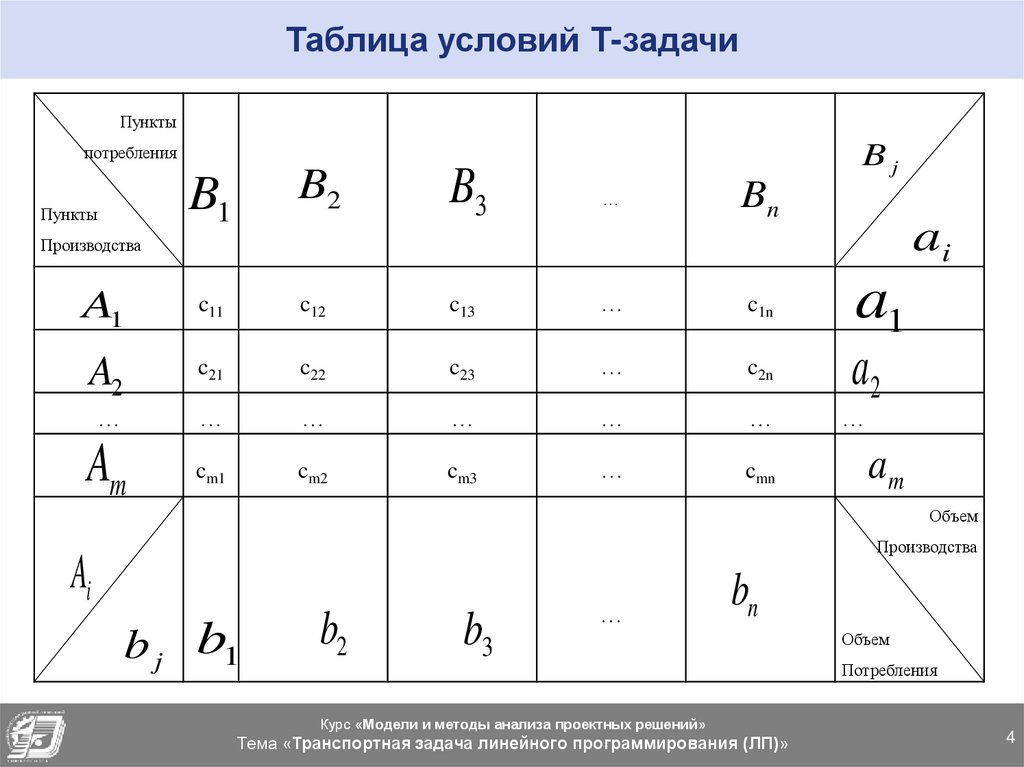
Условия Т-задачи удобнее представить в виде таблицы
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
3

4. Таблица условий Т-задачи

Пункты
Bj
потребления
B3
…
c12
c13
…
c1n
a1
c21
c22
c23
…
c2n
a2
…
…
…
…
…
…
…
Am
cm1
cm2
cm3
…
cmn
B1
B2
A1
c11
A2
Пункты
Bn
ai
Производства
am
Объем
Производства
Ai
b j b1
b2
b3
…
bn
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
Объем
Потребления
4

5. Система ограничений

Пусть xij – количество продукта, перевозимого из пункта в Ai пункт Bj.
Требуется определить множество переменных хij ≥ 0, i=1, 2, …, m; j= 1, 2,…,
n, удовлетворяющих условиям
n
x
j 1
ij
ai , i=1, 2, …, m; (1,1)
m
x b , j=1, 2, …, n,
i 1
ij
(1,2)
j
и таких, что целевая функция достигает минимума.
m
n
L( xij ) cij xij
i 1 j 1
Условия гарантируют полный вывоз продукта из всех пунктов производства и
полное удовлетворение спроса во всех пунктах потребления.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
5

6. План перевозок Т-задачи

Т-задача представляет собой задачу ЛП с (m × n) числом переменных xi
и (m + n) числом ограничений-равенств.
Переменные xij нумеруются с помощью двух индексов и потому набор
{xij}, удовлетворяющий условиям (1.1) и (1.2), записывают в виде
матрицы
.
x11
x
X xij
21
m,n
...
xm1
x12
x22
...
xm 2
... x1n
... x2 n
... ...
... xmn
Матрицу Х называют планом перевозок Т-задачи, а переменные xij –
перевозками. План Хопт, при котором целевая функция минимальна,
называется оптимальным планом.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
6

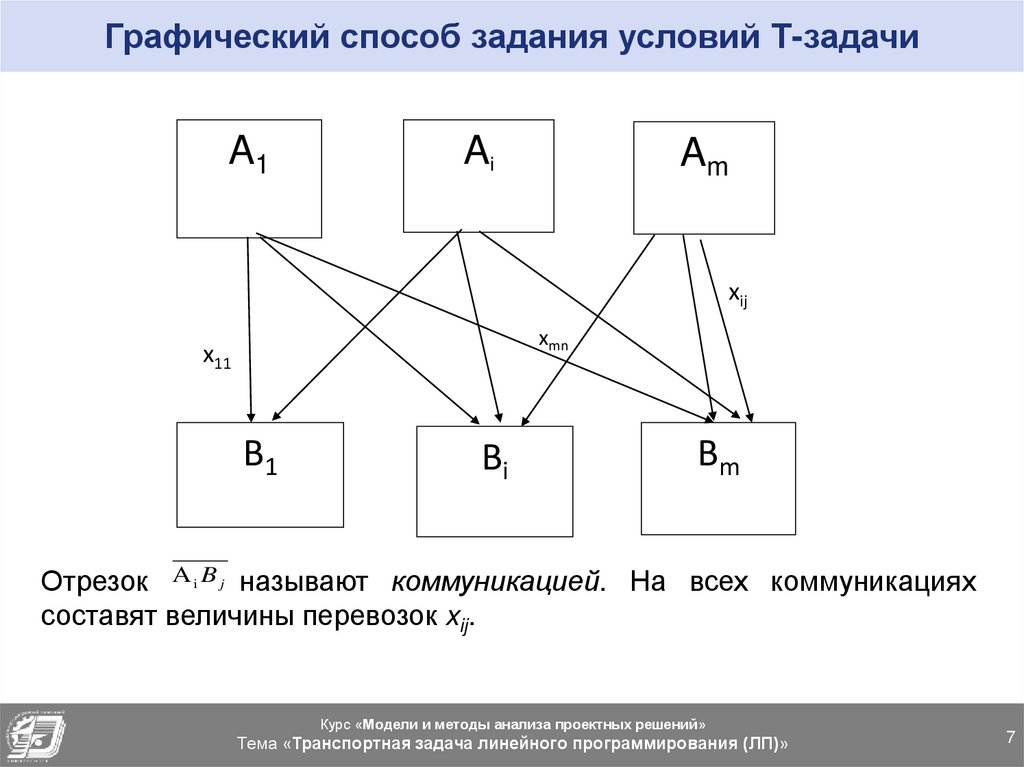
7. Графический способ задания условий Т-задачи

A1
Ai
Am
xij
xmn
x11
B1
Bi
Bm
Отрезок A i B j называют коммуникацией. На всех коммуникациях
составят величины перевозок xij.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
7

8. Вектор производства потребления

Вводят также вектор производства потребления Р0, где
P0T a1 , a 2
..., a m , b1 , ..., bn
Тогда ограничения (1.1) и (1.2) можно записать в векторной форме
m
n
x P P .
.
i 1 j 1
ij ij
0
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
8

9. Коммуникации

Вектор Рij, компоненты которого строятся из коэффициентов при
переменных xij в ограничениях (1.1) и (1.2), называют вектором
коммуникаций:
PijT
0,
0,
...,
0, 1,
0,
...,
0, 1,
0,
0,
0
i
m j
m n
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
9

10. Свойства транспортной задачи.

1.Для разрешимости Т-задачи необходимо и достаточно, чтобы
выполнялось условие баланса
m
n
a b ,
i 1
i
j 1
j
иными словами, объем производства должен быть равен объему
потребления.
2.Ранг системы ограничений (1.1) и (1.2) равен r = m + n – 1.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
10

11. Двойственная транспортная задача

Для Т-задачи, как и для любой задачи ЛП, существует двойственная к
ней -задача.
Переменные -задача обозначим v1, v2 ,…,vn и (-u1), (-u2), …,(- um).
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
11

12. ТЕОРЕМА 3.1.

Т-задача всегда имеет решение или Хопт = xij и Wопт ={v1опт, v2опт, …,
~
vnопт, - u1опт, - u2опт, …, - umопт} – оптимальные решении Т- и T - задач
соответственно, то
m
n
c x
i 1 j 1
ij ijоjо
т
m
о 1
i 1
b j v jооп ai uiооп .
Переменные vj и ui называют потенциалами Ai и Bj для Т-задач.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
12

13. Необходимые и достаточные условия оптимальности плана Т-задачи.

Необходимые и достаточные условия оптимальности плана Тзадачи.
ТЕОРЕМА 3.2. Для оптимальности плана Х0 Т-задачи необходимо и
достаточно существования чисел v1, v2, ..., vn и (-u1), (-u2), ..., ..., (um) таких, что
vj - ui ≤ cij,
i=1, 2, ..., m; j= 1, 2, ..., n,
(1.8)
при этом, если >0, то vj – ui = cij
Эта теорема дает достаточные условия оптимальности плана Х.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
13

14. Экономическая интерпретация теоремы

Разность между потенциалами пунктов Вj и Аi, т.е. величину vj – ui ,
можно рассматривать как приращение ценности единицы продукции
при перевозке из пункта Аi в пункт Bj.
Поэтому если vj - ui ≤ cij, то перевозка по коммуникации
Ai B j
нерентабельна и хij=0.
Если vj - ui = cij, то такая перевозка рентабельна и x ij( 0 ) >0
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
14

15. Транспортная задача с ограниченными пропускными способностями

Пусть dij – пропускная способность коммуникации Ai B j . Тогда
хij ≤ dij
Тd-задача состоит в минимизации целевой функции.
Даже в случае разрешимости Т-задачи Тd-задача может оказаться
неразрешимой, поскольку величины пропускных способностей будут
недостаточны для полного вывоза продукта из пункта Ai (i=1, 2, ... ,m) и
его полного вывоза в пункт Bj ( j=1, 2, ..., n). Поэтому для Тd-задача
вводят еще два условия:
n
d
j 1
ij
ai , i=1, 2, …, m
m
d b , j=1, 2, …, n
i 1
ij
j
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
15

16. ТЕОРЕМА 3.3

Для оптимальности плана Х0 Тd-задача необходимо и достаточно
существование таких чисел v1, v2, ..., vn и (-u1), (-u2), (-um), при
которых
(0)
vj – ui ≤ cij , если xij =0;
(1.12)
(0)
vj – ui = cij , если 0< xij < dij ;
(1.13)
(0)
vj – ui ≥ cij , если xij = dij ;
(1.14)
Смысл условий оптимальности (3.1.12), (3.1.13) и (3.1.14) состоит в
следующем.
Если приращение стоимости продукта vj – ui при перевозке по Ai B j
коммуникации меньше транспортных расходов ci (1.12), то такая
перевозка убыточна, а потому x0ij =0.
Если же приращение стоимости продукта vj – ui больше
транспортных расходов cij (1.14), то эта перевозка прибыльна и ее
величина в оптимальном плане должна быть максимальной, т.е.
xij( 0 ) = dij.
Таким образом, теорема 3.3 по существу выражает принцип
рентабельности для Тd-задачи.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
16

17. Открытые транспортные модели.

Существует ряд практических задач, в которых условие баланса
m
n
a b
i 1
i
j 1
j
не выполняется. Такие модели называются открытыми Т-моделями.
Возможны два случая:
m
1)
n
a b
i 1
i
m
2)
j 1
n
a b
i 1
j
i
j 1
j
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
17

18. Первый случай

В первом случае полное удовлетворение спроса невозможно. Такую
задачу можно привести к обычной Т-задаче следующим образом.
1. Обозначим через rj величину штрафа из-за неудовлетворения
запросов на единицу продукта в пункте Bj.
Тогда требуется минимизировать суммарные затраты:
m
минимизировать
n
с x r y
i 1 j 1
n
x a
при условиях
j 1
ij
ij
n
ij
ij
m
j 1
i
j
для всех i; xij b j j=1, …, n,
i 1
m
где y j b j xij
неудовлетворенный спрос.
i 1
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
18

19. Открытые транспортные модели

. Существует ряд практических задач, в которых условие баланса
m
n
a b
i 1
i
j 1
j
не выполняется. Такие модели называются открытыми Тмоделями. Возможны два случая:
m
1)
n
a b
i
i 1
2) .
m
j 1
n
a b
i 1
j
i
j 1
j
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
19

20. Примеры задач, приводимых к транспортной модели

1. Задачи наилучшего распределения боевых средств
2. Задача перевозки неоднородного продукта на
разнотипном транспорте.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
20

21. Задачи наилучшего распределения боевых средств

Пусть имеется система обслуживания, состоящая из n типов различных
приборов. Обозначим Nj (j= 1,..., n) – количество приборов j-го типа, тогда
общее количество приборов
n
N N.
j 1
j
В систему обслуживания в определенные моменты времени прибывают
заявки разных типов. Обозначим di(t) ( i= 1, ..., m) – число заявок i-го типа,
прибывших в систему в момент времени t.
m
Общее число заявок равно
D di
i 1
Различные приборы имеют разную эффективность (производительность)
при обслуживании соответствующих типов заявок. Обозначим матрицу
эффективностей
M = || μij || i = 1, ..., m; j = 1, ..., n.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
21

22.

Если предположить, что каждый прибор в любой момент времени
обслуживать не более одной заявки, то в данной задаче требуется
распределить свободные приборы по заявкам так, чтобы интегральная
эффективность системы была наибольшей.
Обозначим хij (0 ≤ xij ≤ Nj ) – число приборов j-го типа, отведенных для
обслуживания заявок i-го типа.
Тогда сформулированную выше задачу можно записать таким образом:
минимизировать
m n
x
i 1 j 1
ij ij
при ограничениях
m
n
i 1
j 1
(t )
x
N
;
x
d
ij j ij i ; i = 1, ..., m; j =1, ..., n.
Полученная модель является моделью открытой Т-задачи.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
22

23. Задача перевозки неоднородного продукта на разнотипном транспорте.

Пусть для обеспечения перевозок используют S автохозяйств, в
каждом из которых имеется r типов машин. Допустим, что
разнотипные машины, обладая различными эксплуатационными
характеристиками и разной скоростью, могут доставить любой из m
видов грузов каждому из n потребителей.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
23

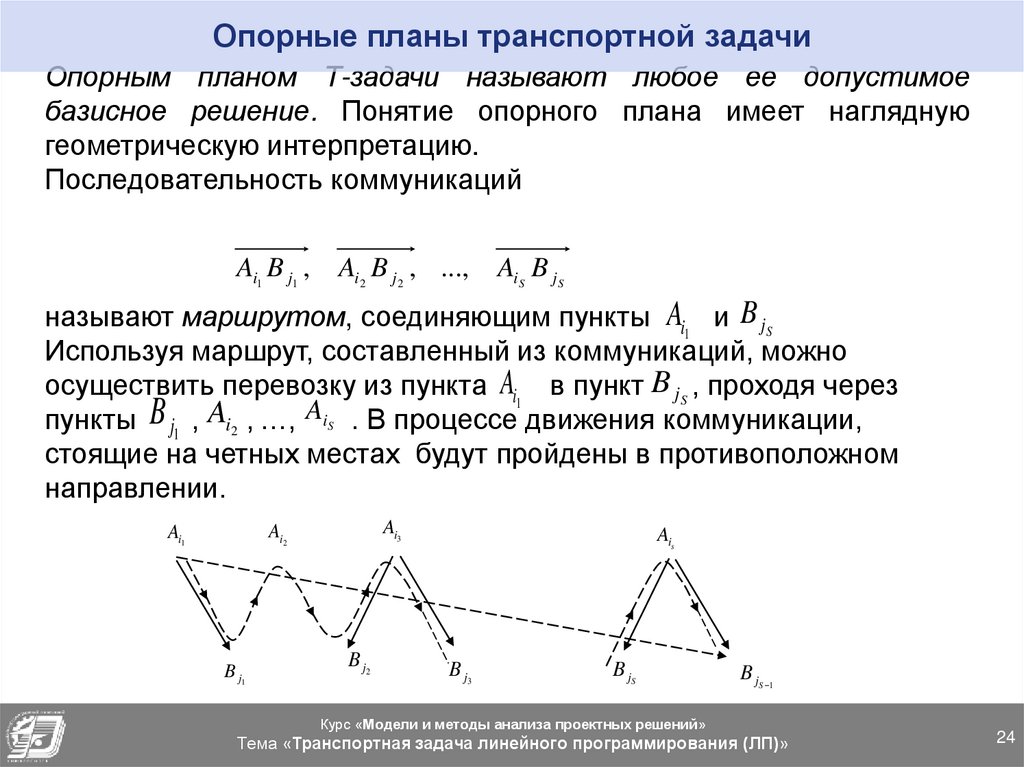
24. Опорные планы транспортной задачи

Опорным планом Т-задачи называют любое ее допустимое
базисное решение. Понятие опорного плана имеет наглядную
геометрическую интерпретацию.
Последовательность коммуникаций
Ai1 B j1 ,
Ai2 B j2 , ...,
AiS B jS
называют маршрутом, соединяющим пункты Ai1 и B jS
Используя маршрут, составленный из коммуникаций, можно
осуществить перевозку из пункта Ai1 в пункт B jS , проходя через
пункты B j1 , Ai2 , …, AiS . В процессе движения коммуникации,
стоящие на четных местах будут пройдены в противоположном
направлении.
Ai3
Ai2
Ai1
B j1
B j2
Ais
B j3
B jS
B jS 1
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
24

25. Замкнутый маршрут

Маршрут, к которому добавлена коммуникация , называется
замкнутым маршрутом, или циклом.
Способ проверки произвольного плана Т-задачи на опорность
основана на следующих теоремах (прямой и обратной).
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
25

26. ТЕОРЕМА 3.4.

Система, составленная из векторов Рij Т-задачи, является линейно
независимой тогда, и только тогда, когда из коммуникаций,
соответствующих этим векторам, нельзя составить замкнутый
маршрут.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
26

27. ТЕОРЕМА 3.5

Вектор Рkl является линейной комбинацией векторов системы R тогда,
и только тогда, когда из векторов этой системы можно составить
маршрут, соединяющий пункты Ak и Вl. Если этот маршрут имеет вид
Ak B j1 , Ai1 B j1 , ..., AiS B jS , AiS Bl
то
Pkl Pkj1 Pi1 j1 Pi1 j2 ... PiS jS PiS l
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
27

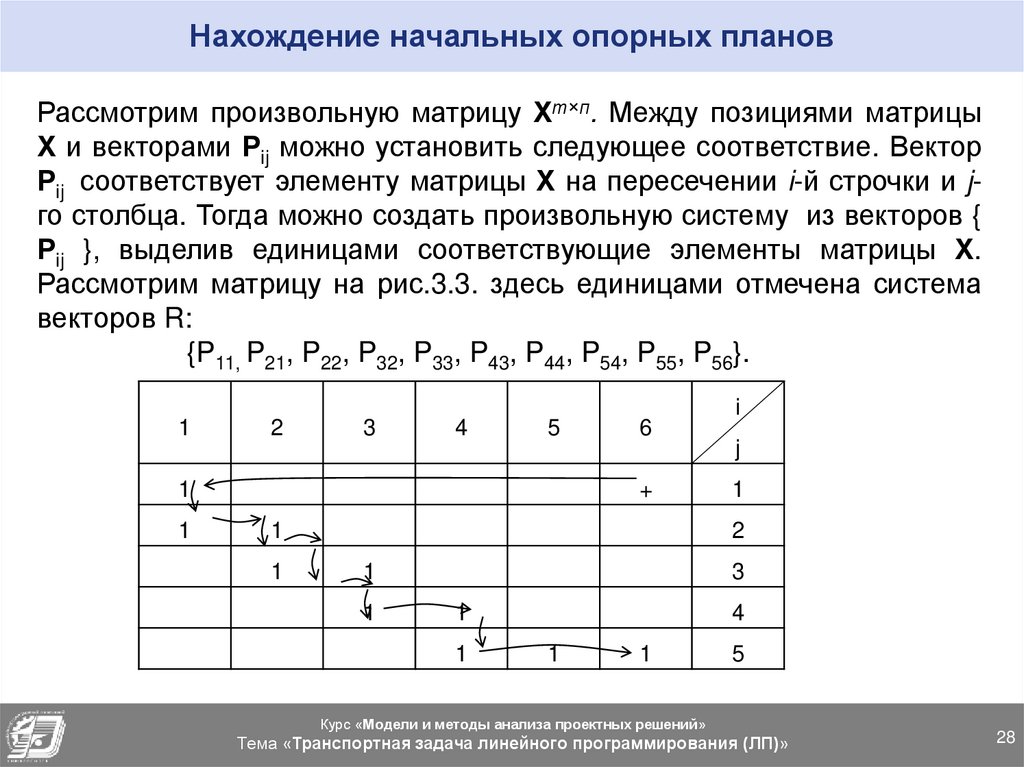
28.   Нахождение начальных опорных планов

Нахождение начальных опорных планов
Рассмотрим произвольную матрицу Хт×п. Между позициями матрицы
Х и векторами Рij можно установить следующее соответствие. Вектор
Рij соответствует элементу матрицы Х на пересечении i-й строчки и jго столбца. Тогда можно создать произвольную систему из векторов {
Рij }, выделив единицами соответствующие элементы матрицы Х.
Рассмотрим матрицу на рис.3.3. здесь единицами отмечена система
векторов R:
{P11, P21, P22, P32, P33, P43, P44, P54, P55, P56}.
1
2
3
4
5
1
1
6
+
1
1
i
j
1
2
1
1
3
1
1
4
1
1
5
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
28

29. Пояснения

При использовании матрицы Х критерий проверки линейной
независимости формулируется так: для линейной независимости
системы векторов {Рij} необходимо и достаточно, чтобы из
ненулевых элементов матрицы Х, отвечающих этим векторам,
невозможно было составить замкнутый маршрут (цикл).
Так как из выделенных единицами позиций нельзя составить
замкнутый маршрут, то данная система линейно независима и
образует базис.
Введем вектор P16, отметив его знаком +. Чтобы разложить P16 по
векторам системы R, составим цепочку из выделенных элементов,
которая замыкается на элементе х16:
P16 = P11 - P21 + P22 - P32 + P33 - P43 + P44 - P54 + P56.
При большом размере матрицы Х визуальное оттискивание
замкнутых цепочек в ней представляет значительные трудности. В
таком случае прибегают к формализованному методу вычеркивания.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
29

30. Метод вычеркивания

Метод вычеркивания позволяет выделить в произвольном плане Х Тзадачи замкнутую цепочку, если она существует.
1.Выделив в плане Х некоторое множество ненулевых элементов,
обозначаемое через S, выясняют, существуют ли во множестве
элементов S циклы.
2. Просматривают одну за другой строки плана Х и вычеркивают
строки, не содержащие элементов S, и строки, которые содержат не
более одного элемента S.
3. Просмотрев все строки плана Х, переходят к столбцам и
вычеркивают те, которые содержат не более одного элемента S. При
этом элементы, содержащиеся в ранее вычеркнутых строках, в
расчет не принимают.
4.Далее повторяют весь процесс, просматривая вначале строки, а
потом столбцы оставшейся после вычеркивания строк и столбцов
подматрицы.
После конечного числа шагов процесс заканчивается одним из
следующих двух исходов: 1)все строки (столбцы) вычеркнуты; 2)
получена подматрица, в каждой строке (столбце) которой
содержится не менее двух элементов S.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
30

31. Пример:

2
3
5
1
1
11
1
1
7
8
1
1
1
1*
1*
1*
6
9
1
1*
2
1
10
1
1
1
1*
3
1
4
1
1*
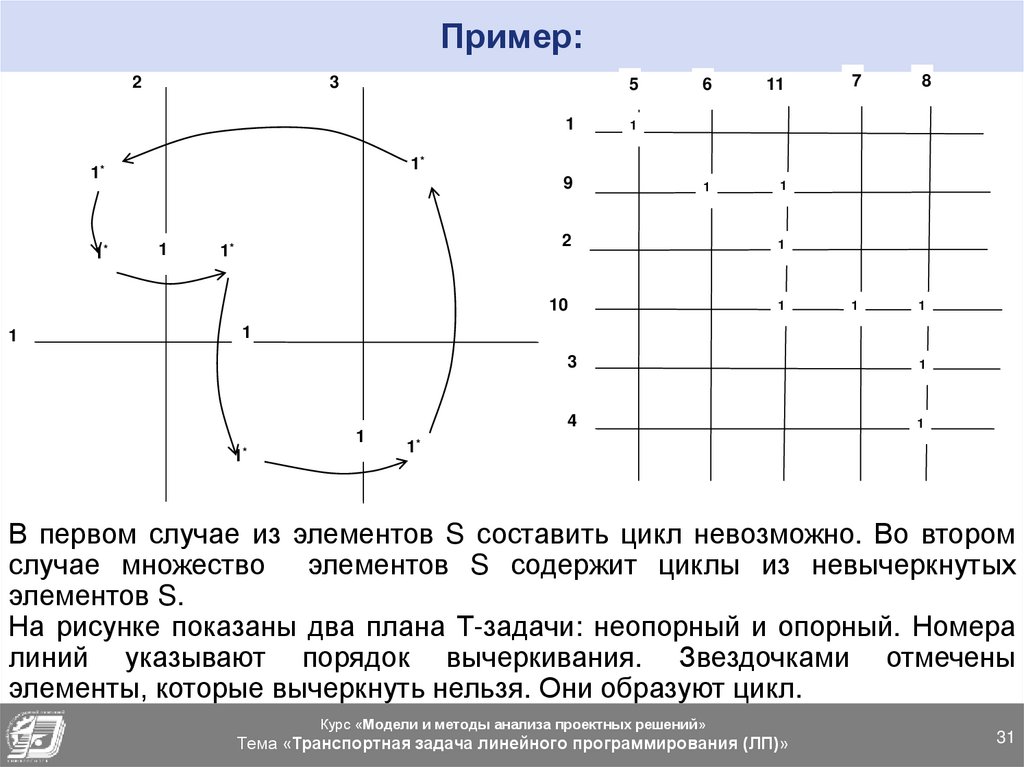
В первом случае из элементов S составить цикл невозможно. Во втором
случае множество элементов S содержит циклы из невычеркнутых
элементов S.
На рисунке показаны два плана Т-задачи: неопорный и опорный. Номера
линий указывают порядок вычеркивания. Звездочками отмечены
элементы, которые вычеркнуть нельзя. Они образуют цикл.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
31

32. Нахождение начальных опорных планов

Метод северо-западного угла используют для нахождения
произвольного опорного плана Т-задачи.
Метод минимального элемента позволяет построить начальный
опорный план Т-задачи и является вариантом метода северозападного угла, учитывающим специфику матрицы С= || сij||.
Метод потенциалов позволяет, исходя из некоторого опорного плана
перевозок, построить за конечное число итераций решение Т-задачи.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
32

33. Метод северо-западного угла

Дана Т-задача с четырьмя пунктами производства {ai}= 1, 2, 3, 4 и
потребителя {bj}= 5, 1, 2, 2. строим матрицу размером 4×4, причем
для
удобства
вычислений
снизу
от
нее
выписываем
неудовлетворенные потребности, а в столбцах справа – остатки
невывезенного продукта
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
33

34. Заполнение таблицы

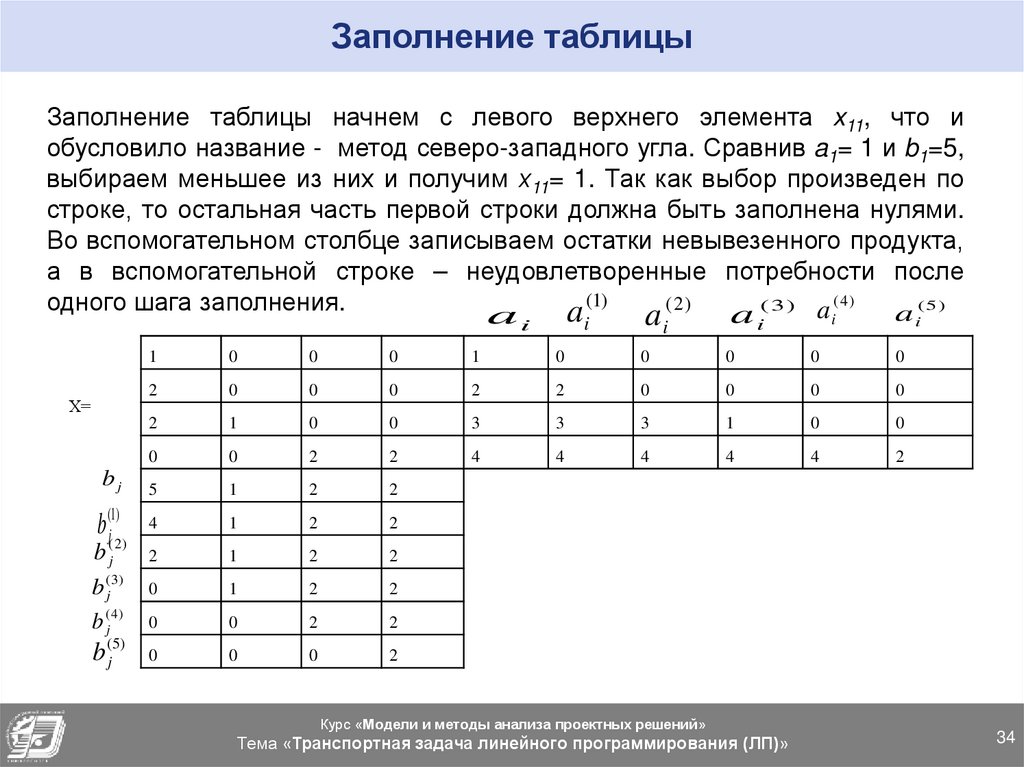
Заполнение таблицы начнем с левого верхнего элемента x11, что и
обусловило название - метод северо-западного угла. Сравнив a1= 1 и b1=5,
выбираем меньшее из них и получим х11= 1. Так как выбор произведен по
строке, то остальная часть первой строки должна быть заполнена нулями.
Во вспомогательном столбце записываем остатки невывезенного продукта,
а в вспомогательной строке – неудовлетворенные потребности после
(1)
(5)
(2)
одного шага заполнения.
( 3) a (4)
a
a
a
ai
i
a
i
i
i
i
Х=
bj
b (j1)
b (j 2 )
b (j3)
b (j 4 )
b
( 5)
j
1
0
0
0
1
0
0
0
0
0
2
0
0
0
2
2
0
0
0
0
2
1
0
0
3
3
3
1
0
0
0
0
2
2
4
4
4
4
4
2
5
1
2
2
4
1
2
2
2
1
2
2
0
1
2
2
0
0
2
2
0
0
0
2
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
34

35. Заполнение таблицы(продолжение)

Переходим ко второй строке и начинаем заполнение с элемента a21.
Сравнивая a2(1)= 2 и b2(1)= 4, выбираем меньшее из них, и потому х21= 2.
остальную часть второй строки заполним нулями. Процесс
заполнения далее продолжаем аналогично.
Полученный план является опорным, так как из его ненулевых
перевозок нельзя составит цепочку. Кроме того, он удовлетворяет
условиям задачи, так как
i=1, 2, 3, 4; j=1, 2, 3, 4.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
35

36. Формальное описание алгоритма.

1.Определяют верхний левый элемент матрицы Х:
х11= min(a1, b1).
Возможны три случая:
если a1< b1 , то х11= a1, и всю первую строку, начиная со второго элемента,
заполняют нулями;
если a1> b1 , то х11= b1, а все оставшиеся элементы первого столбца
заполняют нулями;
если a1= b1 , то х11= a1 = b1, и все оставшиеся элементы первых столбцов и
строки заполняют нулями.
Находим
a1(1) = a1 - х11,
b1(1) = b1 - х11.
На этом один шаг метода заканчивается.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
36

37. Формальное описание алгоритма.

2.Пусть уже проделано k шагов. (k+1)-й шаг состоит в следующем.
Определяют верхний левый элемент незаполненной части матрицы Х.
пусть этот элемент
xλμ(λ + μ = k+2),
причем (k )
хλμ= min { a ( k ), b },
где
1
1
a a x j
(k )
b
(k )
b x
i 1
и
Если a < b , то заполняем нулями λ-ю строку, начиная с (μ +1)-го
элемента. В противном случае заполняем нулями оставшуюся часть μго столбца.
(k )
( k 1)
(k )
( k 1)
b
a
a
Далее вычисляем = - хλμ,
=b - хλμ.. На этом (k+1)-й шаг
заканчивается. Описанный процесс повторяется до тех пор, пока
матрица Х не будет полностью определена (заполнена).
(k )
(k )
j 1
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
37

38. Метод минимального элемента

Метод минимального элемента позволяет построить начальный
опорный план Т-задачи и является вариантом метода северозападного угла, учитывающим специфику матрицы С= || сij||. В отличии
от метода северо-западного угла данный метод позволяет сразу
получить достаточно экономичный план, сокращая общее количество
итераций по его
оптимизации.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
38

39. Формальное описание метода

Элементы матрицы С нумеруют, начиная от минимального в порядке
возрастания, а затем в этом же порядке заполняют матрицу Х0.
Пусть элементом с минимальным порядковым номером оказался
элемент хij= min{ai, bj}.
Возможны три случая:
а) если min{ai, bj} = аi, то оставшуюся часть i-й строки заполняем
нулями;
б) если min{ai, bj} = bj, то оставшуюся часть j-го столбца заполняем
нулями;
в) если ai= bj , то оставшуюся часть строки и столбца заполняем
нулями.
Далее этот процесс повторяют с незаполненной частью матрицы.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
39

40. Формальное описание метода

(k )
x
Пусть элементом с k-м порядковым номером оказался .
Тогда x = min { a ( k ) , b (k ) },
где
1
(k )
a a x ( gj ) , g=1, …, (k-1);
j 1
1
b b xi( l )
(k )
i 1
, l=1, …, (k-1).
Возможны три случая:
(k )
(k )
(k )
(k )
a
x
b
а) < , тогда = a и оставшуюся часть строки λ
заполняем нулями;
(k )
(k )
(k )
a
б) >b , тогда x (k ) = b и оставшуюся часть столбца μ
заполняем нулями;
(k )
(k )
b
a
в) = , тогда оставшуюся часть строки λ и столбца μ
заполняем нулями.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
40

41. Метод потенциалов

Метод потенциалов позволяет, исходя из некоторого опорного плана
перевозок, построить за конечное число итераций решение Т-задачи.
В данном начальном опорном плане каждому пункту ставят в
соответствии некоторое число, называемое его предварительным
потенциалом. Предварительные потенциалы выбирают так, чтобы их
разность для любой пары пунктов Аi и
Bj, связанных основной
коммуникацией, была равна cij. Если окажется, что разность
предварительных потенциалов для всех других коммуникаций
не
превосходит cij, то данный план перевозок – оптимальное решение
задачи. В противном случае указывают способ улучшения опорного
плана Т-задачи.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
41

42. Описание алгоритма метода потенциалов

Алгоритм складывается из предварительного этапа и конечного числа
однотипных итераций.
На предварительном этапе строят начальный опорный план Х0 и
составляют матрицу
С1 = ||cij – (u ( 0 ) – v ( 0) )|| m, n,
i
( 0)
j
(0)
Где v j , u i – предварительные потенциалы пунктов Аi (i = 1, 2, ..., m) и
Bj (j= 1, 2, ..., n).
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
42

43. Связь метода потенциалов с симплекс-методом.

Пусть - некоторый опорный план Т-задачи. Множество, состоящее
из базисных векторов Pij, которые отвечают основным
коммуникациям плана Х, обозначим Кх, т.е. Кх состоит из (т+ п- 1)векторов.
На первом этапе метода потенциалов вычисляют предварительные
потенциалы , , ..., , , ,… , которые удовлетворяют условиям - = cij для
всех векторов Pij Кх . Величина имеет смысл симплекс разности.
Предположим, что для всех Pij Кх. Это означает, что при введении
любого из векторов Pij уменьшить целевую функцию L(X) нельзя, а
поэтому план Х – оптимальный. Если же два некоторых вектора
величина , то при введении вектора в базис можно уменьшить
значение целевой функции L(X).
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
43

44. Связь метода потенциалов с симплекс-методом(продолжение)

Переход к новому базису, который включает вектор Pi j , связан с
построением цепочки, которая замыкается на элементе xi0 j0. Чтобы
определить какой вектор выводится из базиса, разлагают Pi j по
векторам старого базиса. Далее отыскивают
0 0
0 0
xij
xik jk
k min
,
x
x
( ij ) K x ij , i0 j 0
i k j k i0 j 0
(2.2)
где
xik jk- базисное значение переменной при векторе Pi j , выводимом из
базиса;
xik jk i0 j0 - коэффициент при выводимом из базиса векторе Pi j в
разложении для вектора Pi j .
k k
k k
0 0
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
44

45. Опорный план

Опорный план называется вырожденным, если число его ненулевых
перевозок k меньше ранга матрицы ограничений.
В процессе построения начального плана или при его улучшении
очередной план может оказаться вырожденным.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
45

46. Решение транспортной задачи при вырожденном опорном плане

Рассмотрим два случая:
1.Вырожденный план является начальным (Х0). Тогда выбирают
некоторые нулевые элементы матрицы Х0 в качестве базисных
элементов так, чтобы при этом не нарушалось условие опорности:
отсутствие цикла из ненулевых перевозок.
Далее данные элементы матрицы заменяют на ε > 0 (где ε –
произвольное, бесконечно малое число) и рассматривают как обычные
базисные элементы плана.
Задачу решают как невырожденную, а в оптимальном плане вместо ε
пишут нули.
2.Вырожденный план получается при построении Хk+1 ,если цепочка
содержит не менее двух минимальных нечетных элементов. В таком
случае в матрице Хk+1 полагают равным нулю только один из этих
элементов, остальные заменяются на ε и решают задачу как
невырожденную. Если на k-ом шаге θk = ε, то при переходе Хk→ Хk+1
целевая функция не изменяется, а в базис вводится элемент, для
которого перевозка станет равной ε.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
46

47. Пример

Даны: матрица транспортных издержек С = || cij ||, i=1,т, j=1, n,
объемы производства ai. Объемы потребления bij.
ai
1
3
С
6
2
bj
2
4
4
3
9
1
8
3
70 5 45 70
т
Проверяем условие баланса
исходный опорный план Х0:
7 60
5 55
3 40
1 35
n
a b : 190 = 190. Строим
i 1
i
j 1
j
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
47

48. Пример (Продолжение)

60
10
X0
0
0
0 0 0
5 40 0
0 5 35
0 0 35
х11=min {60;70}=60;
х21 = min{55; 70 – 60} = 10;
х22 = min{5; 55 - 10} = 5;
х23= min{45; 55 – 10 - 5}=40;
х33= min{40; 45 - 40} =5;
х34= min{70; 40 – 5} = 35;
х44=35.
Полученный план не вырожденный, так как r=4+4-1=7.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
48

49. Пример (Продолжение)

Начальный опорный план может быть найден также методом
минимального элемента. Этот метод позволяет получить опорный
план с учетом матрицы стоимости перевозок C=|| cij ||. План строим
таким образом, чтобы перевозки хij выполнялись, по возможности, по
маршрутам с минимальной стоимостью. Для этого элементы матрицы
С
ai
1
3
С
6
2
2
4
4
3
9
1
8
3
7 60
5 55
3 40
1 35
bj 70 5 45
70
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
49

50. Пример (Продолжение)

нумеруем, начиная от минимального в порядке возрастания, а затем в
этом же порядке определяем элементы матрицы Х1
х11=min {60;70}=60;
х23 = min{55; 45} = 45;
х44 = min{35; 70}=35;
х12=0;
х41=0;
х21= min{55; 70 – 60}=10;
х42=0;
х43=0;
х34= min{40; 70 - 35} =35;
х22=0;
х32= min{40 – 35; 5} = 5.
Элементы матрицы Х, соответствующие с24, с31, с14, с33, с13, не
рассматриваются, так как исчерпаны все ресурсы и удовлетворены
все потребности.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
50

51. Пример (Продолжение)

Строим опорный план Х0, заполняя xij в порядке полученной
нумерации:
60
10
X0
0
0
0 0 0
0 40 0
5 0 35
0 0 35
Построенный план вырожденный, поскольку количество ненулевых
элементов xij≠0 равно 6, а r=m+n-1=7.
Рассмотрим работу алгоритма на примере 1.10. Решение начинаем с
проверки выполнения условия баланса, т.е. условия разрешимой
задачи:
4
4
a b = 190.
i 1
i
j 1
j
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
51

52. Пример (Продолжение)

Строим начальный опорный план по методу северо-западного угла:
60
10
X0
0
0
0 0 0
5 40 0
0 5 35
0 0 35
Для удобства вычисления потенциалов ui и vj представим графически
план перевозок, соответствующий начальному опорному плану (рис.12).
По соответствующим маршрутам указываем стоимость перевозки cij
единицы груза i-го пункта в j-й. принимаем ui=0 (можно взять любое
число) и, пользуясь соотношением (1.11.7), определяем потенциалы:
u1=0;
c11=1, v1 - u1= c11, v1= 1;
c21=3, v1 – u2= c21, u2= -2;
c22=4, v2 – u2= c22, v2 = 2
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
52

53. Пример (Продолжение)

Рассчитываем элементы оценочной матрицы по соотношению (1.11.6):
cij= cij – (vj – ui);
c12= c12 - v2+ u1 = 2 - 2+0 =0;
c13= c13 – v3+ u1 = 9 + 1-0 =10;
c14= c14 – v4+ u1 = 7+ 2- 0 =13;
и т.д.
Таким образом
0
0 10 13
0
0
0 9
С1
4 7 0 0
6 6 3 0
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
53

54. Пример (Продолжение)

Поскольку в С1 имеются отрицательные элементы, план Х0 не
является оптимальным.
Первая итерация. В матрице Х0, начиная с элемента х32,
соответствующего
в
оценочной
матрице
наибольшему
отрицательному элементу, строим цепочку. Изменяя элементы,
входящие в цепочку, на величину Ө =min{5;5}=5 строим план Х1:
Полученный план является вырожденным. Поскольку в дальнейших
расчетах оперируем невырожденным планом, один из нулей цепочки
заменяем величиной ε≠0. В случае вырожденности при построении
начального опорного плана вводим xij =ε по такой коммуникации,
которая необходима для определения потенциалов ui и vj.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
54

55. Пример (Продолжение)

Выполняем преобразования в матрице С1, предварительно отменив в
ней нули, соответствующие базисным переменным xij≠0 плана Х1, и
строим оценочную матрицу С2:
В оценочной матрице С2 нет отрицательных элементов,
следовательно, план Х1 является оптимальным. Стоимость перевозок
в условных единицах
m
n
i 1
j 1
L cij xij 60*1+ 10*3 + 40*1 + 5*4 + 35*3 + 35*1 = 290.
Курс «Модели и методы анализа проектных решений»
Тема «Транспортная задача линейного программирования (ЛП)»
55

56.

СПАСИБО ЗА ВНИМАНИЕ
© ФГБОУ ВПО ИжГТУ имени М.Т. Калашникова, 2014
© Исенбаева Елена Насимьяновна, 2014